盐析白兔

这个屌丝很懒，什么也没留下！

热门标签

【编程之路】面试必刷TOP101：动态规划（入门）（62-66，Python实现）_链表实现动态规划详解

作者：盐析白兔 | 2024-04-09 06:46:09

踩

链表实现动态规划详解

【面试必刷TOP101】系列包含：

面试必刷TOP101：动态规划（入门）（62-66，Python实现）

62.斐波那契数列
63.跳台阶
- 63.1 动态规划
64.最小花费爬楼梯
- 64.1 动态规划
65.最长公共子序列（二）
- 65.1 动态规划+栈
66.最长公共子串
- 66.1 枚举
- 66.2 动态规划

62.斐波那契数列

小试牛刀

我记得第一次遇到此题是在课堂上，老师拿来讲“递归”的（哈哈哈）。同样的类型的题还有兔子繁殖的问题。大同小异。此题将用三个方法来解决，从入门到会做。

62.1 递归

在这里插入图片描述

class Solution:
    def Fibonacci(self , n: int) -> int:
        if n == 0 or n == 1:
            return n
        else:
            return self.Fibonacci(n-1) + self.Fibonacci(n-2)
1
2
3
4
5
6

时间复杂度： $O(2^n)$
空间复杂度：递归栈的空间。

62.2 记忆化搜索

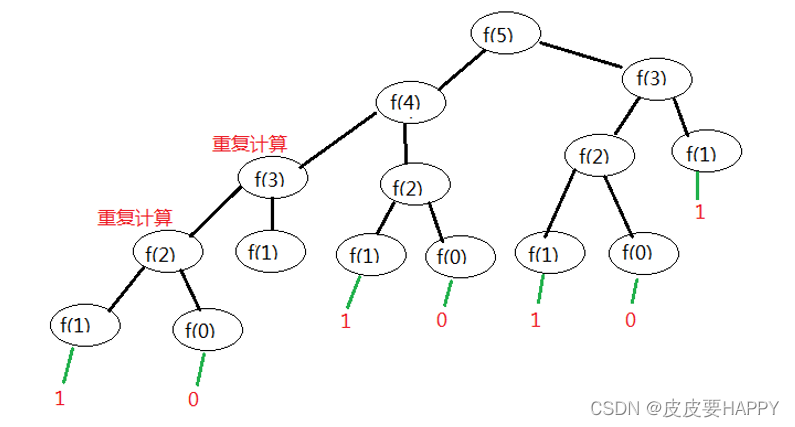
方法一中，存在很多重复计算，因为为了改进，就把计算过的保存下来。那么用什么保存呢？一般会想到map，但是此处不用牛刀，此处用数组就好了。

class Solution:
    def __init__(self):
        self.a = [0] * 50
    def Fibonacci(self , n: int) -> int:
        if n <= 2:
            return 1
        if self.a[n] > 0:
            return self.a[n]
        self.a[n] = self.Fibonacci(n-1) + self.Fibonacci(n-2)
        return self.a[n]
1
2
3
4
5
6
7
8
9
10

时间复杂度： $O (n)$
空间复杂度： $O (n)$

62.3 动态规划

虽然方法二可以解决此题了，但是如果想让空间继续优化，那就用动态规划，优化掉递归栈空间。方法二是从上往下递归的然后再从下往上回溯的，最后回溯的时候来合并子树从而求得答案。那么动态规划不同的是，不用递归的过程，直接从子树求得答案。过程是从下往上。

class Solution:
    def __init__(self):
        self.a = [0] * 50
    def Fibonacci(self , n: int) -> int:
        self.a[1] = 1
        self.a[2] = 1
        for i in range(3,n+1):
            self.a[i] = self.a[i-1] + self.a[i-2]
        return self.a[n]
1
2
3
4
5
6
7
8
9

时间复杂度： $O (n)$
空间复杂度： $O (n)$

发现计算 f[5] 的时候只用到了 f[4] 和 f[3], 没有用到 f[2]、f[1]、f[0]，所以保存 f[2]、f[1]、f[0] 是浪费了空间。只需要用3个变量即可。

class Solution:
    def Fibonacci(self , n: int) -> int:
        a = 1
        b = 1
        c = 1
        for i in range(3,n+1):
            c = a + b
            a = b
            b = c
        return c
1
2
3
4
5
6
7
8
9
10

时间复杂度： $O (n)$
空间复杂度： $O (1)$

63.跳台阶

小试牛刀

63.1 动态规划

class Solution:
    def jumpFloor(self , number: int) -> int:
        a = 1
        b = 2
        if number == 1:
            return 1
        if number == 2:
            return 2
        for i in range(3,number+1):
            c = a + b
            a = b
            b = c
        return c
1
2
3
4
5
6
7
8
9
10
11
12
13

64.最小花费爬楼梯

小试牛刀

64.1 动态规划

动态规划算法的基本思想是：将待求解的问题分解成若干个相互联系的子问题，先求解子问题，然后从这些子问题的解得到原问题的解；对于重复出现的子问题，只在第一次遇到的时候对它进行求解，并把答案保存起来，让以后再次遇到时直接引用答案，不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果。

题目同样考察斐波那契数列的动态规划实现，不同的是题目要求了最小的花费，因此我们将方案统计进行递推的时候只记录最小的开销方案即可。

step 1：可以用一个数组记录每次爬到第i阶楼梯的最小花费，然后每增加一级台阶就转移一次状态，最终得到结果。
step 2：（初始状态）因为可以直接从第0级或是第1级台阶开始，因此这两级的花费都直接为0。
step 3：（状态转移）每次到一个台阶，只有两种情况，要么是它前一级台阶向上一步，要么是它前两级的台阶向上两步，因为在前面的台阶花费我们都得到了，因此每次更新最小值即可，转移方程为：dp[i]=min(dp[i−1]+cost[i−1],dp[i−2]+cost[i−2])。

class Solution:
    def minCostClimbingStairs(self , cost: List[int]) -> int:
        a = [0] * (len(cost) + 1)
        a[0] = 0
        a[1] = 0
        for i in range(2,len(cost)+1):
            a[i] = min(a[i-1] + cost[i-1], a[i-2] + cost[i-2])
        return a[len(cost)]
1
2
3
4
5
6
7
8

时间复杂度： $O (n)$ ，其中 n 为给定的数组长度，遍历一次数组。
空间复杂度： $O (n)$ ，辅助数组 a 的空间。

65.最长公共子序列（二）

小试牛刀

65.1 动态规划+栈

step 1：优先检查特殊情况。
step 2：获取最长公共子序列的长度可以使用动态规划，我们以 $d p [i] [j]$ 表示在 $s 1$ 中以 $i$ 结尾， $s 2$ 中以 $j$ 结尾的字符串的最长公共子序列长度。
step 3：遍历两个字符串的所有位置，开始状态转移：若是 $i$ 位与 $j$ 位的字符相等，则该问题可以变成 $d p [i - 1] [j - 1] + 1$ ，即到此处为止最长公共子序列长度由前面的结果加 1。
step 4：若是不相等，说明到此处为止的子串，最后一位不可能同时属于最长公共子序列，毕竟它们都不相同，因此我们考虑换成两个子问题， $d p [i] [j - 1]$ 或者 $d p [i - 1] [j]$ ，我们取较大的一个就可以了。
step 5：得到最长长度后，获取第二个辅助数组b，直接从 $d p$ 数组最后一位开始，每次比较当前位置与其 左、上、左上 的关系，然后将符合要求的字符加入栈中，符合要求即来自 $d p$ 表格左上方的字符。
step 6：最后将栈中的字符拼接即可得到最长公共子序列，注意检查子序列是否为空。

class Solution:
    def LCS(self , s1: str, s2: str) -> str:
        if len(s1) == 0 or len(s2) == 0:
            return '-1'
        len1 = len(s1)
        len2 = len(s2)
        # dp[i][j] 表示：第一个字符串到第 i 位，第二个字符串到第 j 位为止的最长公共子序列长度
        dp = [[0] * (len2+1) for i in range(len1+1)]
        # 遍历两个字符串每个位置的最长长度
        for i in range(1,len1+1):
            for j in range(1,len2+1):
                # 遇到的两个字符相等
                if s1[i-1] == s2[j-1]:
                    # 来自于左上方
                    dp[i][j] = dp[i-1][j-1] + 1
                # 遇到的两个字符不同
                else:
                    # 来自左边或上边的最大值
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        # 从动态规划得到的数组末尾开始往回
        i = len1
        j = len2
        s = []
        while dp[i][j] != 0:
            # 来自于左方向
            if dp[i][j] == dp[i-1][j]:
                i = i - 1
            # 来自于上方向
            elif dp[i][j] == dp[i][j-1]:
                j = j - 1
            # 来自于左上方向。左上方向才是字符相等的情况。
            elif dp[i][j] > dp[i-1][j-1]:
                i = i - 1
                j = j - 1
                s.append(s1[i])
        s.reverse()
        if len(s) == 0:
            return '-1'
        else:
            return ''.join(s)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

时间复杂度： $O(n^2)$ ，最坏复杂度为构造辅助数组 $d p$ 两层循环。
空间复杂度： $O(n^2)$ ，辅助二维数组 $d p$ 与栈空间最大为 $O(n^2)$ 。

66.最长公共子串

小试牛刀

注意这题求的是最长公共子串，不是最长公共子序列，子序列可以是不连续的，但子串一定是连续的。

66.1 枚举

最简单直观的方式大概就是枚举了，枚举所有的子串进行比较，但是太复杂了。其实找子串不用一样完全枚举，还可以尝试改良一下。

step 1：我们完全可以遍历两个字符串的所有字符串作为起始。
step 2：然后同时开始检查字符是否相等，相等则不断后移，增加子串长度，如果不等说明以这两个为起点的子串截止了，不会再有了。
step 3：后续比较长度维护最大值即可。

class Solution:
    def LCS(self , str1: str, str2: str) -> str:
        length = 0
        # 遍历 s1 每个起点
        for i in range(len(str1)):
            # 遍历 s2 每个起点
            for j in range(len(str2)):
                temp = 0
                temps = ''
                x = i
                y = j
                while x < len(str1) and y < len(str2) and str1[x] == str2[y]:
                    temps = temps + str1[x]
                    x = x + 1
                    y = y + 1
                    temp = temp + 1
                if length < temp:
                    length = temp
                    res = temps
        return res
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

时间复杂度： $O(m^2n)$ ，其中 m 是 str1 的长度，n 是 str2 的长度，分别枚举两个字符串每个字符作为起点，后续检查子串长度最坏需要花费 O(m)。
空间复杂度： $O (n)$ ，res 属于返回必要空间，temps 属于临时辅助空间，最坏情况下长度为 n。

上面的写法运行会超时，下面给出一种不超时的写法。下面的这种写法我觉得已经是滑动窗口的范畴了，这里的窗口是一直在增大的，不会减小。

class Solution:
    def LCS(self , str1: str, str2: str) -> str:
        # 让 str1 为较长的字符串
        if len(str1) < len(str2):
            str1, str2 = str2, str1
        res = ''
        max_len = 0
        for i in range(len(str1)):
            if str1[i-max_len: i+1] in str2:
                res = str1[i-max_len: i+1]
                max_len = max_len + 1
        return res
1
2
3
4
5
6
7
8
9
10
11
12

66.2 动态规划

step 1：我们可以用 $d p [i] [j]$ 表示 在 str1 中以第 $i$ 个字符结尾，在 str2 中以第 $j$ 个字符 结尾时的公共子串长度。
step 2：遍历两个字符串填充 $d p$ 数组，转移方程为：如果遍历到的该位两个字符相等，则此时长度等于两个前一位长度 +1， $d p [i] [j] = d p [i - 1] [j - 1] + 1$ ，如果遍历到该位时两个字符不相等，则置为 0，因为这是子串，必须连续相等，断开要重新开始。
step 3：每次更新 $d p [i] [j]$ 后，我们维护最大值，并更新该子串结束位置。
step 4：最后根据最大值结束位置即可截取出子串。

class Solution:
    def LCS(self , str1: str, str2: str) -> str:
        # dp[i][j]表示：到 str1 第 i 个，到 str2 第 j 个，为止的公共子串长度
        dp = [[0] * (len(str2)+1) for i in range(len(str1)+1)]
        max = 0
        pos = 0
        for i in range(1,len(str1)+1):
            for j in range(1,len(str2)+1):
                # 如果该两位相同
                if str1[i-1] == str2[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = 0
                # 更新最大长度
                if dp[i][j] > max:
                    max = dp[i][j]
                    pos = i - 1
        return str1[pos-max+1: pos+1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

时间复杂度： $O (mn)$ ，其中 m 是 str1 的长度，n 是 str2 的长度，遍历两个字符串所有字符。
空间复杂度： $O (mn)$ ，dp 数组大小为 $m * n$ 。

遗憾的是，上述的这种写法并没有全部AC。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/盐析白兔/article/detail/390951