devbox
盐析白兔
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【Python数据结构系列】❤️《栈（顺序栈与链栈）》——❤️知识点讲解+代码实现_用python语言顺序栈和链栈的程序实现

作者：盐析白兔 | 2024-05-12 04:04:43

赞

踩

用python语言顺序栈和链栈的程序实现

灵魂拷问：为什么要学数据结构？
数据结构，直白地理解，就是研究数据的存储方式。数据存储只有一个目的，即为了方便后期对数据的再利用。因此，数据在计算机存储空间的存放，决不是胡乱的，这就要求我们选择一种好的方式来存储数据，而这也是数据结构的核心内容。
可以说，数据结构是一切编程的基本。学习数据结构是学习一种思想：如何把现实问题转化为计算机语言的表示。
对于学计算机的朋友来说，学习数据结构是基本功。而对于非计算机专业，但是未来想往数据分析、大数据方向发展、或者在Python的使用上能有一个大的跨越的朋友来说，学习数据结构是一种非常重要的逻辑思维能力的锻炼，在求职、职业发展、问题解决等方面都能有潜移默化的大帮助。

数据结构——栈（顺序栈与链栈）

数据结构——栈（顺序栈与链栈）

第一章 栈的基础知识

栈和队列，严格意义上来说，也属于线性表，因为它们也都用于存储逻辑关系为 “一对一” 的数据。使用栈结构存储数据，讲究“先进后出”，即最先进栈的数据，最后出栈；使用队列存储数据，讲究 “先进先出”，即最先进队列的数据，也最先出队列。既然栈和队列都属于线性表，根据线性表分为顺序表和链表的特点，栈也可分为顺序栈和链栈，队列也分为顺序队列和链队列，这些内容都会在本章做详细讲解。

1. 栈存储结构

1.1 栈的基本介绍

同顺序表和链表一样，栈也是用来存储逻辑关系为 “一对一” 数据的线性存储结构，如图1所示。

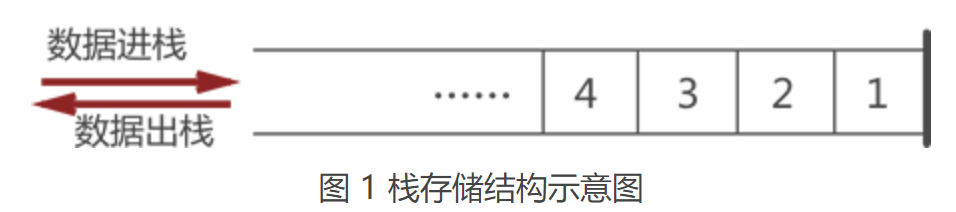
Image Name
　
　　从图 1 我们看到，栈存储结构与之前所学的线性存储结构有所差异，这缘于栈对数据 “存” 和 “取” 的过程有特殊的要求：

（1）栈只能从表的一端存取数据，另一端是封闭的，如图 1 所示；

（2）在栈中，无论是存数据还是取数据，都必须遵循"先进后出"的原则，即最先进栈的元素最后出栈。拿图 1 的栈来说，从图中数据的存储状态可判断出，元素 1 是最先进的栈。因此，当需要从栈中取出元素 1 时，根据"先进后出"的原则，需提前将元素 3 和元素 2 从栈中取出，然后才能成功取出元素 1。
　　因此，我们可以给栈下一个定义，即栈是一种只能从表的一端存取数据且遵循 “先进后出” 原则的线性存储结构。

通常，栈的开口端被称为栈顶；相应地，封口端被称为栈底。因此，栈顶元素指的就是距离栈顶最近的元素，拿图 2 来说，栈顶元素为元素 4；同理，栈底元素指的是位于栈最底部的元素，图 2 中的栈底元素为元素 1。

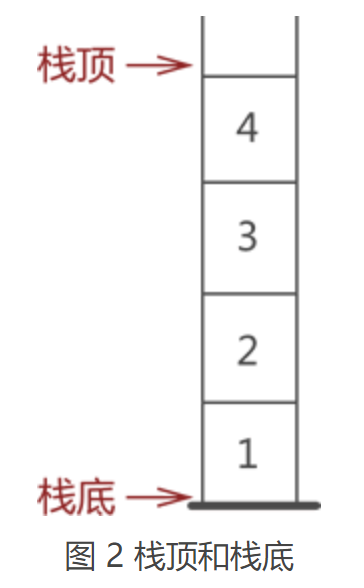
Image Name

1.2 进栈和出栈

基于栈结构的特点，在实际应用中，通常只会对栈执行以下两种操作：

（1）向栈中添加元素，此过程被称为"进栈"（入栈或压栈）；

（2）从栈中提取出指定元素，此过程被称为"出栈"（或弹栈）；

1.3 栈的具体实现

栈是一种 “特殊” 的线性存储结构，因此栈的具体实现有以下两种方式：

（1）顺序栈：采用顺序存储结构可以模拟栈存储数据的特点，从而实现栈存储结构；

（2）链栈：采用链式存储结构实现栈结构；
　
　
　　两种实现方式的区别，仅限于数据元素在实际物理空间上存放的相对位置，顺序栈底层采用的是数组，链栈底层采用的是链表。有关顺序栈和链栈的具体实现会在后续章节中作详细讲解。

1.4 栈的应用

基于栈结构对数据存取采用 “先进后出” 原则的特点，它可以用于实现很多功能。
　　
　　例如，我们经常使用浏览器在各种网站上查找信息。假设先浏览的页面 A，然后关闭了页面 A 跳转到页面 B，随后又关闭页面 B 跳转到了页面 C。而此时，我们如果想重新回到页面 A，有两个选择：

（1）重新搜索找到页面 A；

（2）使用浏览器的"回退"功能。浏览器会先回退到页面 B，而后再回退到页面 A。
　
　　浏览器 “回退” 功能的实现，底层使用的就是栈存储结构。当你关闭页面 A 时，浏览器会将页面 A 入栈；同样，当你关闭页面 B 时，浏览器也会将 B入栈。因此，当你执行回退操作时，才会首先看到的是页面 B，然后是页面 A，这是栈中数据依次出栈的效果。

不仅如此，栈存储结构还可以帮我们检测代码中的括号匹配问题。多数编程语言都会用到括号（小括号、中括号和大括号），括号的错误使用（通常是丢右括号）会导致程序编译错误，而很多开发工具中都有检测代码是否有编辑错误的功能，其中就包含检测代码中的括号匹配问题，此功能的底层实现使用的就是栈结构。

同时，栈结构还可以实现数值的进制转换功能。例如，编写程序实现从十进制数自动转换成二进制数，就可以使用栈存储结构来实现。

2. 顺序栈及基本操作（包含入栈和出栈）

2.1 顺序栈的基础介绍

顺序栈，即用顺序表实现栈存储结构。通过前面的学习我们知道，使用栈存储结构操作数据元素必须遵守 “先进后出” 的原则，本节就 “如何使用顺序表模拟栈以及实现对栈中数据的基本操作（出栈和入栈）” 给大家做详细介绍。

如果你仔细观察顺序表（底层实现是数组）和栈结构就会发现，它们存储数据的方式高度相似，只不过栈对数据的存取过程有特殊的限制，而顺序表没有。

例如，我们先使用顺序表（a 数组）存储 {1,2,3,4}，存储状态如图 1 所示：

Image Name

同样，使用栈存储结构存储 {1,2,3,4}，其存储状态如图 2 所示：

Image Name

通过图 1 和图 2 的对比不难看出，使用顺序表模拟栈结构很简单，只需要将数据从 a 数组下标为 0 的位置依次存储即可。

从数组下标为 0 的模拟栈存储数据是常用的方法，从其他数组下标处存储数据也完全可以，这里只是为了方便初学者理解。

了解了顺序表模拟栈存储数据后，接下来看如何模拟栈中元素出栈的操作。由于栈对存储元素出栈的次序有"先进后出"的要求，如果想将图 1 中存储的元素 1 从栈中取出，需先将元素 4、元素 3 和元素 2 依次从栈中取出。

这里给出使用顺序表模拟栈存储结构常用的实现思路，即在顺序表中设定一个实时指向栈顶元素的变量（一般命名为 top），top 初始值为 -1，表示栈中没有存储任何数据元素，及栈是"空栈"。一旦有数据元素进栈，则 top 就做 +1 操作；反之，如果数据元素出栈，top 就做 -1 操作。

2.2 顺序栈元素"入栈"

比如，还是模拟栈存储 {1,2,3,4} 的过程。最初，栈是"空栈"，即数组是空的，top 值为初始值 -1，如图 3 所示：

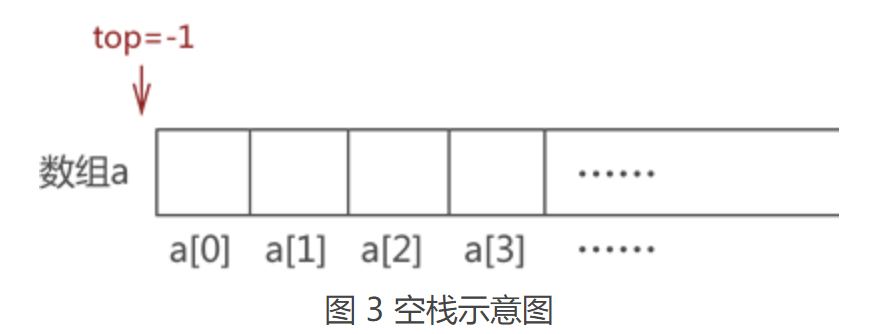
Image Name

首先向栈中添加元素 1，我们默认数组下标为 0 一端表示栈底，因此，元素 1 被存储在数组 a[1] 处，同时 top 值 +1，如图 4 所示：

Image Name

采用以上的方式，依次存储元素 2、3 和 4，最终，top 值变为 3，如图 5 所示：

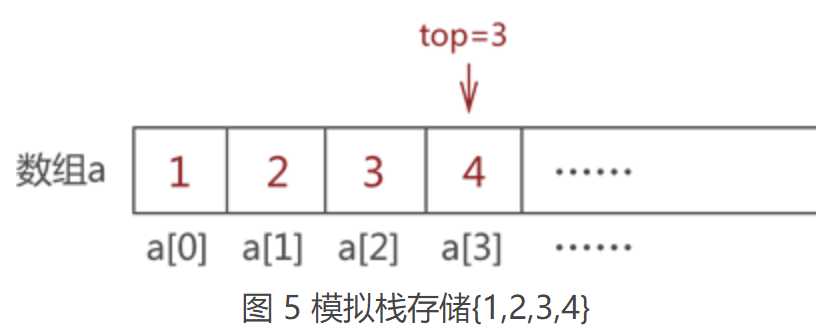
Image Name

2.3 顺序栈元素"出栈"

其实，top 变量的设置对模拟数据的 “入栈” 操作没有实际的帮助，它是为实现数据的 “出栈” 操作做准备的。

比如，将图 5 中的元素 2 出栈，则需要先将元素 4 和元素 3 依次出栈。需要注意的是，当有数据出栈时，要将 top 做 -1 操作。因此，元素 4 和元素 3 出栈的过程分别如图 6a) 和 6b) 所示：

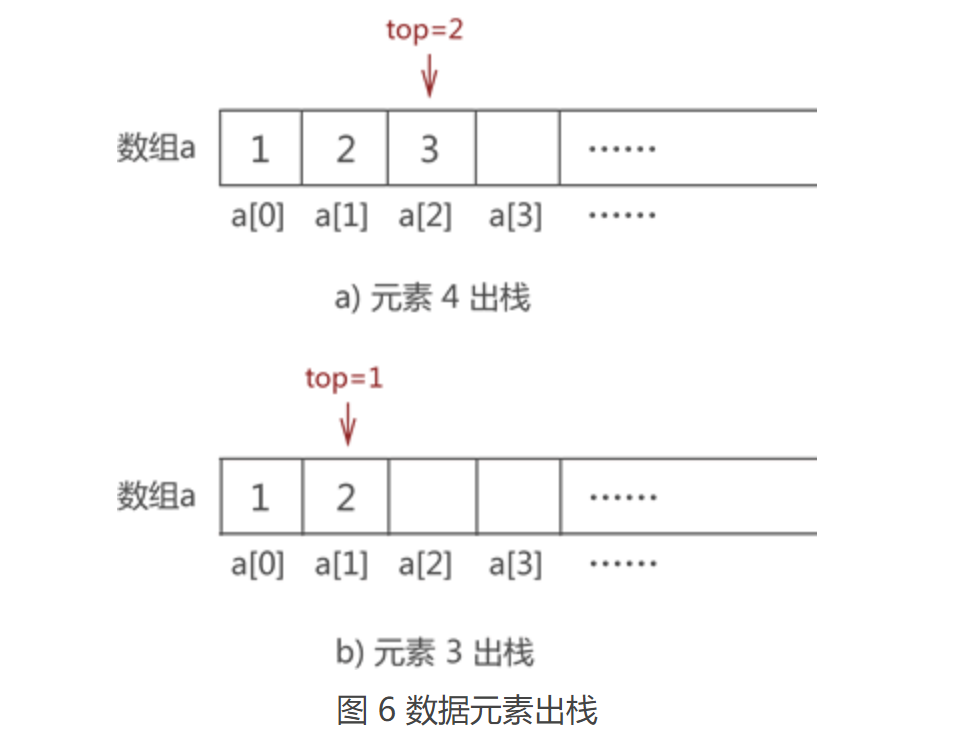
Image Name

注意，图 6 数组中元素的消失仅是为了方便初学者学习，其实，这里只需要对 top 值做 -1 操作即可，因为 top 值本身就表示栈的栈顶位置，因此 top-1 就等同于栈顶元素出栈。并且后期向栈中添加元素时，新元素会存储在类似元素 4 这样的旧元素位置上，将旧元素覆盖。

关于顺序栈Python编程实现代码可参考↓（个人编写，仅供参考，欢迎提出宝贵建议）

任务一：顺序栈的表示和实现（难度：★）

实现基本功能：（包括但不限于，可以根据自己能力继续扩展）

（1）初始化空栈

（2）判断栈是否为空

（3）返回栈顶元素

（4）返回栈的长度

（5）进栈（又称压栈、入栈）

（6）出栈

（7）清空栈

代码实现：

#!/usr/bin/env python
# -*- coding: utf-8 -*- 
# @Time : 2021/7/27 13:52 
# @Author : vaxtiandao
# @File : sqStack_21.py

# -*-coding:utf-8-*-

# 定义顺序栈
class sqStack:
    # 初始化栈
    def __init__(self, MAXSIZE):
        self.MAXSIZE = MAXSIZE
        self.data = [None] * self.MAXSIZE
        self.top = -1

    # 判断当前栈是否为空
    def is_empty(self):
        return self.top == -1

    def gettop(self):
        if self.is_empty():
            print("当前顺序栈为空")
            return None
        else:
            return self.data[self.top]

    # 入栈
    def Push(self, item):
        # 判断栈是否已满
        if self.top == self.MAXSIZE - 1:
            return "sqStack is full."
        self.data[self.top+1] = item
        self.top += 1

    # 列表入栈
    def ListPush(self, x):
        # 判断栈是否已满
        if self.top == self.MAXSIZE - 1:
            return "sqStack is full."
        for i in range((len(x))):
            self.Push(x[i])

    # 出栈
    def Pop(self):
        # 判断栈是否为空
        if self.is_empty():
            return "sqStack is empty"
        rs = self.data[self.top]
        self.top -= 1
        return rs

    # 输出栈的长度
    def size(self):
        return self.top + 1

    # 输出栈内元素
    def display(self):
        # 判断栈是否为空
        if self.is_empty():
            print("当前顺序栈为空", end=" ")
        else:
            print("当前链表元素为：", end="")
        for i in range(self.top+1):
            print(self.data[i], end=" ")
        print()

    # 清空栈
    def clear(self):
        self.data = [None] * self.MAXSIZE
        self.top = -1


if __name__ == '__main__':
    print('---------------------------------')
    # 初始化一个长度为20的顺序栈
    s = sqStack(20)
    print("初始化栈：", s)
    print('---------------------------------')
    # 判断当前栈是否为空
    print("当前栈是否为空：", s.is_empty())
    print('---------------------------------')
    # 输出栈的元素
    s.display()
    print('---------------------------------')
    print("入栈前栈内元素：", end="")
    s.display()
    # 入栈
    s.Push(1)
    s.Push(10)
    s.Push(100)
    # 输出当前栈内的元素
    print("入栈后栈内元素：", end="")
    s.display()
    print('---------------------------------')
    print("当前栈的长度为：", s.size())
    print('---------------------------------')
    print("队列入栈前栈内元素：", end="")
    s.display()
    s.ListPush([1, 2, 3, 4])
    print("队列入栈后栈内元素：", end="")
    s.display()
    print('---------------------------------')
    print("当前栈顶元素为：", s.gettop())
    print('---------------------------------')
    # 顶端元素出栈
    print("出栈前栈内元素：", end="")
    s.display()
    print("出栈元素为：", s.Pop())
    print("出栈后栈内元素：", end="")
    s.display()
    print('---------------------------------')
    # 输出当前栈内的元素
    s.display()
    print('---------------------------------')
    s.clear()
    s.display()
    print('---------------------------------')


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119

实现效果：
在这里插入图片描述

3. 链栈及基本操作（包含入栈和出栈）详解

3.1 链栈的基本介绍

链栈，即用链表实现栈存储结构。

链栈的实现思路同顺序栈类似，顺序栈是将数顺序表（数组）的一端作为栈底，另一端为栈顶；链栈也如此，通常我们将链表的头部作为栈顶，尾部作为栈底，如图 1 所示：
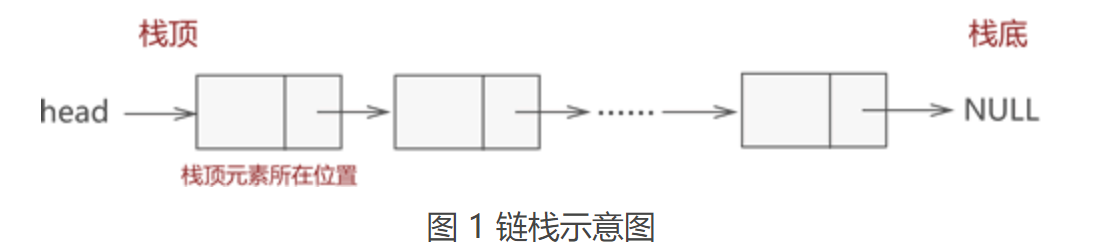
Image Name
　　将链表头部作为栈顶的一端，可以避免在实现数据 “入栈” 和 “出栈” 操作时做大量遍历链表的耗时操作。

链表的头部作为栈顶，意味着：

（1）在实现数据"入栈"操作时，需要将数据从链表的头部插入；

（2）在实现数据"出栈"操作时，需要删除链表头部的首元节点；
　
因此，链栈实际上就是一个只能采用头插法插入或删除数据的链表。

3.2 链栈元素入栈

例如，将元素 1、2、3、4 依次入栈，等价于将各元素采用头插法依次添加到链表中，每个数据元素的添加过程如图 2 所示：

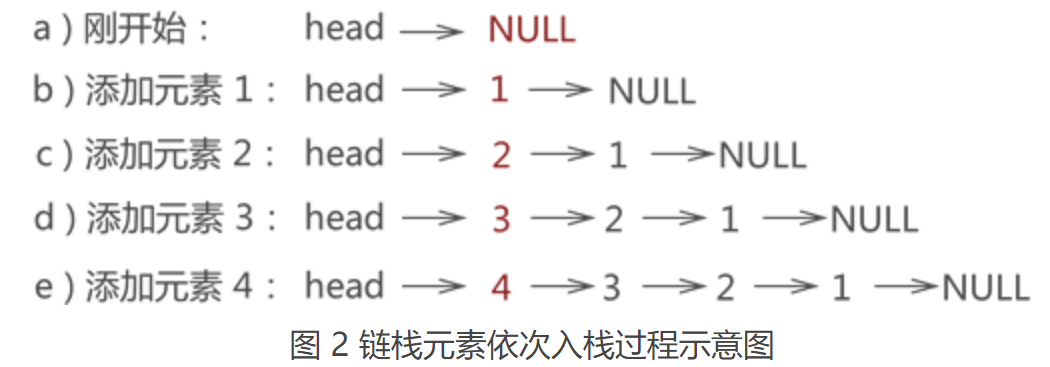
Image Name

3.3 链栈元素出栈

例如，图 2e) 所示的链栈中，若要将元素 3 出栈，根据"先进后出"的原则，要先将元素 4 出栈，也就是从链表中摘除，然后元素 3 才能出栈，整个操作过程如图 3 所示：

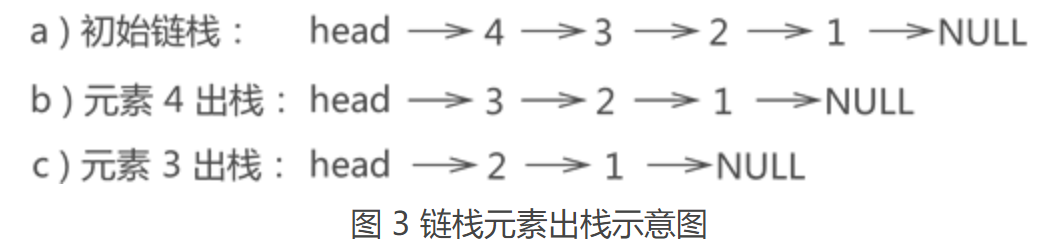
Image Name
关于链栈Python编程实现代码可参考↓（个人编写，仅供参考，欢迎提出宝贵建议）

任务二：链栈的表示和实现（难度：★★）

实现基本功能：（跟顺序栈一样）

（1）初始化空栈

（2）判断栈是否为空

（3）返回栈顶元素

（4）返回栈的长度

（5）进栈（又称压栈、入栈）

（6）出栈

（7）清空栈

#!/usr/bin/env python
# -*- coding: utf-8 -*- 
# @Time : 2021/7/27 14:47 
# @Author : vaxtiandao
# @File : liStack.py

# 定义链栈节点
class Node(object):
    # 初始化链栈
    def __init__(self, data):
        self.data = data
        self.next = None


# 定义链栈
class linkstack(object):

    # 初始化链栈
    def __init__(self):
        self.top = None

    # 判断链栈是否为空
    def is_empty(self):
        return self.top == None

    # 清空链栈
    def clear(self):
        self.top = None

    # 返回当前栈的长度
    def size(self):
        i = 0
        tempnode = self.top
        while tempnode is not None:
            tempnode = tempnode.next
            i += 1
        return i

    # 元素入栈
    def push(self, item):
        node = Node(item)
        node.next = self.top
        self.top = node

    # 栈顶元素出栈
    def pop(self):
        x = self.top.data
        self.top = self.top.next
        return x

    # 获取栈顶元素
    def gettop(self):
        return self.top.data

    # 输出当前栈内元素
    def display(self):
        if self.top == None:
            print("当前栈内元素为空", end="")
        else:
            print("当前栈内元素为：", end="")
        tempnode = self.top
        while tempnode is not None:
            print(tempnode.data, end=" ")
            tempnode = tempnode.next
        print()


if __name__ == "__main__":
    print("-----------------------")
    s1 = linkstack()
    print("初始化的栈为：", s1)
    print("-----------------------")
    print("入栈前的链栈元素为：", end="")
    s1.display()
    s1.push(1)
    s1.push(2)
    s1.push(3)
    s1.push(4)
    s1.push(5)
    s1.push(6)
    print("入栈后的链栈元素为：", end="")
    s1.display()
    print("-----------------------")
    print("当前栈顶元素为：", s1.gettop())
    print("-----------------------")
    print("当前链栈的长度为：", s1.size())
    print("-----------------------")
    print("出栈前的链栈元素为：", end="")
    s1.display()
    print("出栈元素为：", s1.pop())
    print("出栈后的链栈元素为：", end="")
    s1.display()
    print("-----------------------")
    print("清空前的链栈元素为：", end="")
    s1.display()
    s1.clear()
    print("清空后的链栈元素为：", end="")
    s1.display()
    print("-----------------------")
    print("当前链栈是否为空：", s1.is_empty())
    print("-----------------------")


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102

实现效果：
在这里插入图片描述

4.栈的应用（难度：★★）

应用1：括号匹配问题

检验算法借助一个栈，每当读入一个左括号，则直接入栈，等待相匹配的同类右括号；每当读入一个右括号，若与当前栈顶的左括号类型相同，则二者匹配，将栈顶的左括号出栈，直到表达式扫描完毕。

在处理过程中，还要考虑括号不匹配出错的情况。例如，当出现 (()[]) 这种情况时，由于前面入栈的左括号均已知和后面出现的右括号相匹配，栈已空，因此最后扫描的右括号不能得到匹配；出现 [([]) 这种错误，当表达式扫描结束时，栈中还有一个左括号没有匹配；出现 (()] 这种错误显然是栈顶的左括号和最后的右括号不匹配。

测试案例：（小伙伴们需要拿以下三个案例测试自己写的代码哈！）
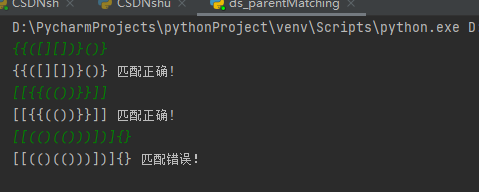
　　案例1：{{([][])}()}
　　案例2：[[{{(())}}]]
　　案例3：[[(()(()))])]{}

运行结果：

Image Name
关于此题编程实现代码可参考↓（个人编写，仅供参考，欢迎提出宝贵建议）

#!/usr/bin/env python
# -*- coding: utf-8 -*- 
# @Time : 2021/7/28 10:14 
# @Author : vaxtiandao
# @File : ds_parentMatching.py


# 定义顺序栈
class sqStack:
    # 初始化栈
    def __init__(self, MAXSIZE):
        self.MAXSIZE = MAXSIZE
        self.data = [None] * self.MAXSIZE
        self.top = -1

    # 判断当前栈是否为空
    def is_empty(self):
        return self.top == -1

    def gettop(self):
        if self.is_empty():
            print("当前顺序栈为空")
            return None
        else:
            return self.data[self.top]

    # 入栈
    def Push(self, item):
        # 判断栈是否已满
        if self.top == self.MAXSIZE - 1:
            return "sqStack is full."
        self.data[self.top + 1] = item
        self.top += 1

    # 列表入栈
    def ListPush(self, x):
        # 判断栈是否已满
        if self.top == self.MAXSIZE - 1:
            return "sqStack is full."
        for i in range((len(x))):
            self.Push(x[i])

    # 出栈
    def Pop(self):
        # 判断栈是否为空
        if self.is_empty():
            return "sqStack is empty"
        rs = self.data[self.top]
        self.top -= 1
        return rs

    # 输出栈的长度
    def size(self):
        return self.top + 1

    # 输出栈内元素
    def display(self):
        # 判断栈是否为空
        if self.is_empty():
            print("当前顺序栈为空", end=" ")
        else:
            print("当前链表元素为：", end="")
        for i in range(self.top + 1):
            print(self.data[i], end=" ")
        print()

    # 清空栈
    def clear(self):
        self.data = [None] * self.MAXSIZE
        self.top = -1


def matching(strings):  # 输入是一串字符
    bktStack = sqStack(60)  # 创建类实例
    flag = 1
    opens = "{[("
    closes = "}])"
    # 对于每个输入字符
    for i in strings:
        # 遇到左括号，就将其压栈
        if i in opens:
            bktStack.Push(i)
        # 遇到右括号
        elif i in closes:
            # 若已没左括号与之匹配
            if bktStack.is_empty():
                # 不匹配，结束
                return False
            # 左括号按什么顺序入，右括号应按相反顺序消掉。
            # 如果匹配，右括号消的始终是栈顶括号。
            # 弹栈bktStack.pop()，判断栈顶左括号与当前右括号是否匹配
            if closes.index(i) != opens.index(bktStack.Pop()):
                # 不匹配，结束
                return False
    # 若一直没有return而是遍历了一遍，且没有多余左括号留在栈中，则说明匹配。反之不匹配。
    return bktStack.is_empty()


# 判断返回的是True还是False
def check(strings):
    if matching(strings):
        print("%s 匹配正确!" % strings)
    else:
        print("%s 匹配错误！" % strings)

if __name__ == "__main__":
    # 测试函数
    for i in range(4):
        stringa = input()
        check(stringa)


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111

实现效果：
在这里插入图片描述

应用2：十进制转二进制

当将一个十进制整数M转换为二进制数时，在计算过程中，把M与2求余得到的二进制数的各位依次进栈，计算完毕后将栈中的二进制数依次出栈输出，输出结果就是待求得的二进制数。

测试案例：
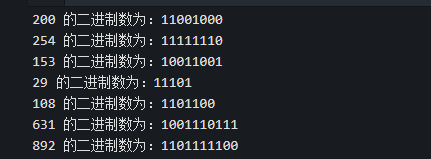
　　[200, 254, 153, 29, 108, 631, 892]

运行结果：

Image Name
关于此题编程实现代码可参考↓（个人编写，仅供参考，欢迎提出宝贵建议）

#!/usr/bin/env python
# -*- coding: utf-8 -*- 
# @Time : 2021/7/28 10:31 
# @Author : vaxtiandao
# @File : ds_10to2.py


# 定义顺序栈
class sqStack:
    # 初始化栈
    def __init__(self, MAXSIZE):
        self.MAXSIZE = MAXSIZE
        self.data = [None] * self.MAXSIZE
        self.top = -1

    # 判断当前栈是否为空
    def is_empty(self):
        return self.top == -1

    def gettop(self):
        if self.is_empty():
            print("当前顺序栈为空")
            return None
        else:
            return self.data[self.top]

    # 入栈
    def Push(self, item):
        # 判断栈是否已满
        if self.top == self.MAXSIZE - 1:
            return "sqStack is full."
        self.data[self.top + 1] = item
        self.top += 1

    # 列表入栈
    def ListPush(self, x):
        # 判断栈是否已满
        if self.top == self.MAXSIZE - 1:
            return "sqStack is full."
        for i in range((len(x))):
            self.Push(x[i])

    # 出栈
    def Pop(self):
        # 判断栈是否为空
        if self.is_empty():
            return "sqStack is empty"
        rs = self.data[self.top]
        self.top -= 1
        return rs

    # 输出栈的长度
    def size(self):
        return self.top + 1

    # 输出栈内元素
    def display(self):
        # 判断栈是否为空
        if self.is_empty():
            print("当前顺序栈为空", end=" ")
        else:
            print("当前链表元素为：", end="")
        for i in range(self.top + 1):
            print(self.data[i], end=" ")
        print()

    # 清空栈
    def clear(self):
        self.data = [None] * self.MAXSIZE
        self.top = -1


if __name__ == "__main__":
    s = sqStack(20)
    data = int(input("请输入要转换成二进制的数字： "))
    while data != 0:
        ys = data % 2
        s.Push(ys)
        data = data // 2

    while s.top != -1:
        print(s.Pop(), end='')


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83

实现效果：
在这里插入图片描述

应用3

十进制转N进制（应用2的拓展）
　　当将一个十进制整数M转换为N进制数时，在计算过程中，把M与N求余得到的N进制数的各位依次进栈，计算完毕后将栈中的N进制数依次出栈输出，输出结果就是待求得的N进制数。

测试案例：
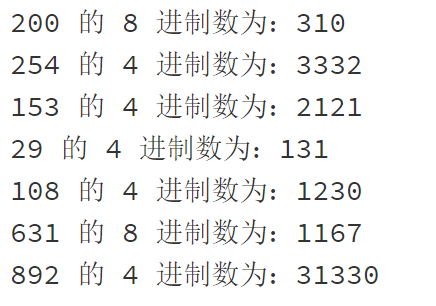
　　测试数：[200, 254, 153, 29, 108, 631, 892]
　　进制：[4, 8, 16]

自由搭配即可，这里我主要使用了random.choice()来对测试数要转换的进制随机取数，测试代码如下所示，仅供参考；

Image Name

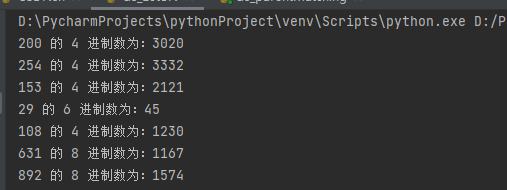
运行结果：

Image Name
关于此题编程实现代码可参考↓（个人编写，仅供参考，欢迎提出宝贵建议）

#!/usr/bin/env python
# -*- coding: utf-8 -*- 
# @Time : 2021/7/28 10:32 
# @Author : vaxtiandao
# @File : ds_10toN.py


# 定义顺序栈
class sqStack:
    # 初始化栈
    def __init__(self, MAXSIZE):
        self.MAXSIZE = MAXSIZE
        self.data = [None] * self.MAXSIZE
        self.top = -1

    # 判断当前栈是否为空
    def is_empty(self):
        return self.top == -1

    def gettop(self):
        if self.is_empty():
            print("当前顺序栈为空")
            return None
        else:
            return self.data[self.top]

    # 入栈
    def Push(self, item):
        # 判断栈是否已满
        if self.top == self.MAXSIZE - 1:
            return "sqStack is full."
        self.data[self.top + 1] = item
        self.top += 1

    # 列表入栈
    def ListPush(self, x):
        # 判断栈是否已满
        if self.top == self.MAXSIZE - 1:
            return "sqStack is full."
        for i in range((len(x))):
            self.Push(x[i])

    # 出栈
    def Pop(self):
        # 判断栈是否为空
        if self.is_empty():
            return "sqStack is empty"
        rs = self.data[self.top]
        self.top -= 1
        return rs

    # 输出栈的长度
    def size(self):
        return self.top + 1

    # 输出栈内元素
    def display(self):
        # 判断栈是否为空
        if self.is_empty():
            print("当前顺序栈为空", end=" ")
        else:
            print("当前链表元素为：", end="")
        for i in range(self.top + 1):
            print(self.data[i], end=" ")
        print()

    # 清空栈
    def clear(self):
        self.data = [None] * self.MAXSIZE
        self.top = -1


def divideByN(number, base):
    digits = "0123456789ABCDEF"
    remstack = sqStack(100)
    while number > 0:
        rem = number % base
        remstack.Push(rem)
        number = number // base
    newString = ""
    while not remstack.is_empty():
        newString = newString + digits[remstack.Pop()]
    return newString


import random

numbers = [200, 254, 153, 29, 108, 631, 892]
bases = [4, 8, 6]
for number in numbers:
    base = random.choice(bases)
    print("%d 的 %d 进制数为：%s" % (number, base, divideByN(number, base)))


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93

实现效果：
在这里插入图片描述

回顾数据结构专栏往期内容：【Python数据结构系列】《线性表》——知识点讲解+代码实现

其他专栏精彩内容：
【建议收藏系列】爆肝3w字带你理解什么叫运维~

10分钟教你如何自动化操控浏览器——Selenium测试工具

【一周掌握Flask框架学习笔记】Flask概念及基础

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/盐析白兔/article/detail/557498
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号