数据结构——栈的详细介绍_完整的栈结构

一、栈的结构和概念

栈：栈是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

二、 栈的两种构建方式

①、用数组进行构建

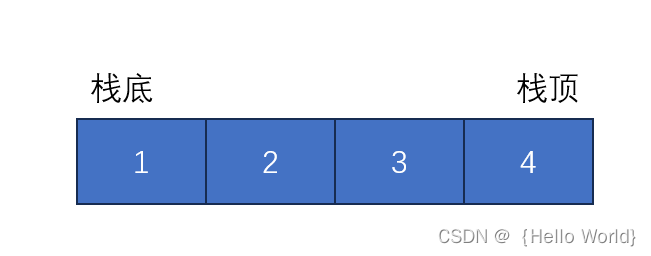
②、用链表进行构建

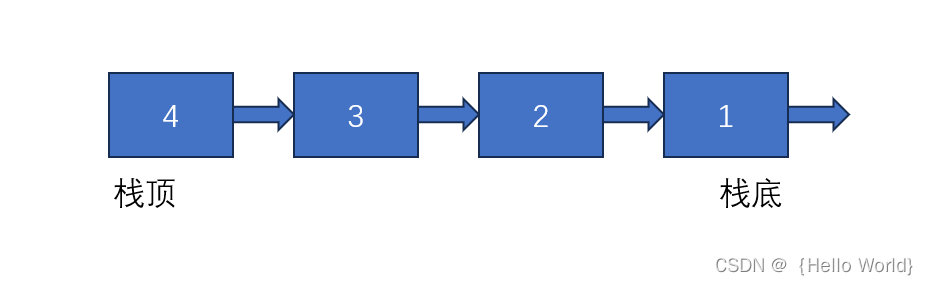
本篇我们采用数组构建的方式为大家进行讲解。本篇博客主要从栈的初始化、栈的销毁、压栈出栈等七个方面为大家全面进行栈的讲解。

//初始化
void InitST(ST* pst);
//销毁
void DestoryST(ST* pst);
//压栈
void PushST(ST* pst, STDatatype x);
//出栈
void PopST(ST* pst);
//判空
bool STEmpty(ST* pst);
//获取栈顶元素
STDatatype TopST(ST* pst);
//获取栈的size
int STSize(ST* pst);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

三、栈的创建

typedef struct STack
{
	STDatatype* a;//数组
	int capacity;//容量
	int top;//栈顶元素的下一个
}ST;
1
2
3
4
5
6

我们采用结构体的方式创建一个结构体成员变量，其中定义了数组指针a,capacity容量，和top。其中a指向的是栈的开始位置，capacity指向的是栈的结束位置，至于top,则既可以指向栈顶位置，也可以指向栈顶元素的下一个位置，这取决于你对其，如何进行初始化。

四、栈的初始化

栈的初始化中，最为重要的一步便是如何对pst->top进行相应的初始化，如果我们将pst->top初始化为0，则top将指向栈顶元素的下一个位置。但是如果我们将其初始化为-1，则top将指向栈顶元素。但是如果将其初始化为-1，也会带来一些不必要的麻烦，例如一些不懂的栈结构的人，可能会以为这里初始化错误。所以我们在这里将其初始化为0.

void InitST(ST* pst)
{
	assert(pst);
	pst->a = NULL;
	pst->capacity = 0;//栈顶元素的下一个位置
	pst->top = 0;
}
1
2
3
4
5
6
7

五、栈的销毁

利用free函数将开辟的内存空间进行释放，并将其置为NULL,并把capacity和top置为0。

void DestoryST(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;
	pst->capacity = pst->top = 0;
}
1
2
3
4
5
6
7

六、压栈

由于栈的后进先出特性，我们便只能对栈顶元素进行出栈操作，不能随意的对其他元素进行出栈操作。出栈函数非常简单，首先是扩容部分，如果数组内存不够，便对其进行扩容操作。然后在栈顶处，插入数据即可。

void PushST(ST* pst, STDatatype x)
{
	if (pst->top == pst->capacity)
	{
		int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
		STDatatype *tmp = (STDatatype*)realloc(pst->a, sizeof(STDatatype) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		pst->a = tmp;
		pst->capacity = newcapacity;
	}
	//插入数据
	pst->a[pst->top] = x;
	pst->top++;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

七、出栈

出栈操作，我们直接对pst->top进行–操作即可。但是，这里需要注意的是当数组元素全部删除完毕之后，便不能对其进行删除操作了，所以这里需要对其进行判空。

oid PopST(ST* pst)
{
	assert(pst);
	assert(!STEmpty(pst));
	pst->top--;
}
1
2
3
4
5
6

八、判空

直接判断pst->top是否等于0，如果pst->top等于0则返回true,否则返回false。

bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}
1
2
3
4
5

九、获取栈顶元素

这里需要注意的是由于我们定义的是pst->top=0,即表示的是栈顶元素的下一个位置，所以当我们想要获取栈顶元素时，我们需要对其进行==-1操作==，返回栈顶元素。

//获取栈顶元素
STDatatype TopST(ST* pst)
{
	assert(pst);
	assert(!STEmpty(pst));
	return pst->a[pst->top-1];
}
1
2
3
4
5
6
7

十、获取栈的size

直接将pst->top进行返回操作。

//获取栈的size
int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}

1
2
3
4
5
6
7