双目立体视觉空间坐标精度分析_双目相机图像坐标测量精度

参考链接：https://zhuanlan.zhihu.com/p/362718946

本文主要参考链接博主的理论推导，并按照自己的理解作分析和修正

一、考虑问题：

1. 双目立体视觉系统的精度由那些因素决定？

2. X/Y/Z三个方向的精度都是一样的吗？如果不是一样，哪个方向精度更好呢？

最常见的情况下，双目立体视觉的最终输出是左相机坐标系下的XYZ坐标，本篇便以这三个分量为精度分析对象。

首先，做一些变量的定义：

b ：基线长度，单位mm

f ：焦距

x, y ：像点坐标（以像主点为原点）

X, Y, Z ：相机坐标系下的坐标，单位mm

d ：视差

我们先看这三个分量的求解公式：

$$Z=\frac{bf}{d},X=\frac{Z}{f}x,Y=\frac{Z}{f}y$$

从公式可知，在硬件参数 b, f 固定的情况下， XYZ 的值和像点坐标值直接相关，XYZ 的精度实际上是像点精度下的空间偏差值，因此我们以像点精度为基本（最小）精度单位。

二、对博主的推导作修正：

当变量定义如下

像素x代表的是尺寸大小，单位mm

焦距f代表物理尺寸，单位mm

视差d代表物理尺寸，单位mm

才能使用博主的推导公式，下面对Z方向的精度推导作解释。

假设像点 x,y 的精度（像素尺寸）为 $s_x,s_y$ ，视差 d 的精度为 $s_d$ 。通常认为 x,y 的精度是相同的，即$s_x=s_y=s$ ，而视差的精度一般来说可以用公式

$$s_d=\frac{s_x}{\sqrt{2}}$$

Z方向精度

首先对于 Z ，自变量是 d ，我们对 d 求偏导，可得

$$\frac{\partial Z}{\partial d}=-\frac{bf}{d^2}=-\frac{Z^2}{bf}$$

$\partial Z/\partial d$
的单位是mm/mm，物理意义为每毫米视差值代表的空间距离大小，需要再乘以视差精度 $s_d$，才能得出单个视差精度代表的空间距离大小，单位mm/pix

可得：

$$s_Z=\frac{Z}{b}\frac{Z}{f}{s}_d=\frac{Z}{b}\frac{Z}{f}\frac{s_x}{\sqrt{2}}$$

可知 Z 方向精度和 Z 的平方正相关，即和物体离相机的距离的平方正相关（严格来说是 Z
方向距离）。

假设$q=\frac{Z}{b},m=\frac{Z}{f}$ ，则 q
是我们所熟知的基高比的倒数， m 是影像的尺度（即GSD，一个像素代表的空间尺寸），这个公式显示，基高比和GSD对 Z 方向精度起着关键作用，更大的基高(1/q)和更小的GSD (m)有助于提高 Z 方向精度。这可以用于指导双目立体视觉系统的设计。

同理参考博主的推导过程，可得出XY方向精度。

三、推导简化

上述的推导需要知道相机的像素和焦距的实际尺寸，比较麻烦。

通常情况下，标定文件中的内参数据都是以pix为单位，下面以像素pix为单位作推导

当变量定义如下

像素x代表的是像素坐标，单位pix

焦距f代表像素比值，单位pix

视差d代表像素比值，单位pix

Z方向精度

首先对于 Z ，自变量是 d ，我们对 d 求偏导，可得

$$\frac{\partial Z}{\partial d}=-\frac{bf}{d^2}=-\frac{Z^2}{bf}$$

此时 $\partial Z/\partial d$
的单位是mm/pix，物理意义为单个像素pix代表的空间距离大小，需要再除以$\sqrt{2}$，才能得出单个视差精度代表的空间距离大小

可得：

$$s_Z=\frac{1}{\sqrt{2}}\frac{Z}{b}\frac{Z}{f}$$

可知 Z 方向精度和 Z
的平方正相关，即和物体离相机的距离的平方正相关（严格来说是 Z
方向距离）。

XY方向精度

同理，对于 X ，自变量是 Z 和 x ，我们对 Z 和 x 求偏导，可得

$$\frac{\partial X}{\partial Z}=\frac{x}{f},\frac{\partial X}{\partial x}=\frac{Z}{f}$$

X 方向精度可表示为

$$s_X=\sqrt{{(\frac{x}{f}{s}_Z)}^2+{(\frac{Z}{f})}^2}$$

同理， Y 方向精度可表示为

$$s_Y=\sqrt{{(\frac{y}{f}{s}_Z)}^2+{(\frac{Z}{f})}^2}$$

把$s_Z=\frac{Z^2}{\sqrt{2}bf},X=\frac{Z}{f}x,Y=\frac{Z}{f}y$代入公式，可得

$$s_X=\frac{Z}{f}\sqrt{1+{(\frac{xZ}{\sqrt{2}fb})}^2}=\frac{Z}{f}\sqrt{1+{(\frac{X}{\sqrt{2}b})}^2}$$

$$s_Y=\frac{Z}{f}\sqrt{1+{(\frac{yZ}{\sqrt{2}fb})}^2}=\frac{Z}{f}\sqrt{1+{(\frac{Y}{\sqrt{2}b})}^2}$$

可以看出，X,Y方向的精度不仅跟Z的距离正相关，还跟各自的X,Y方向距离正相关。

Y/Z精度曲线

为了更清晰的观察Y/Z方向精度随着 Z 值变化的趋势，我们来做一个仿真，计算并绘制 Z 和 Y 方向（Y 方向和X方向等尺度，趋势一致）的精度曲线。

根据实际案例参数数据分析

案例一：

Y = 58 mm， Y方向58毫米处的精度

f = 275 pix

b = 32 mm

绘制的精度曲线如下：

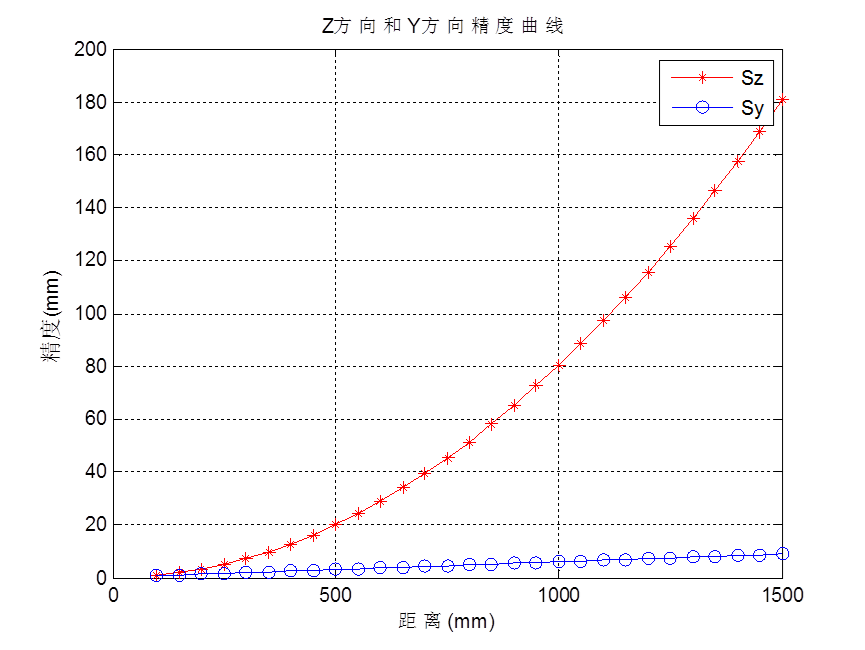
案例二：

Y = 580 mm，Y方向580毫米处的精度

f = 275 pix

b = 32 mm

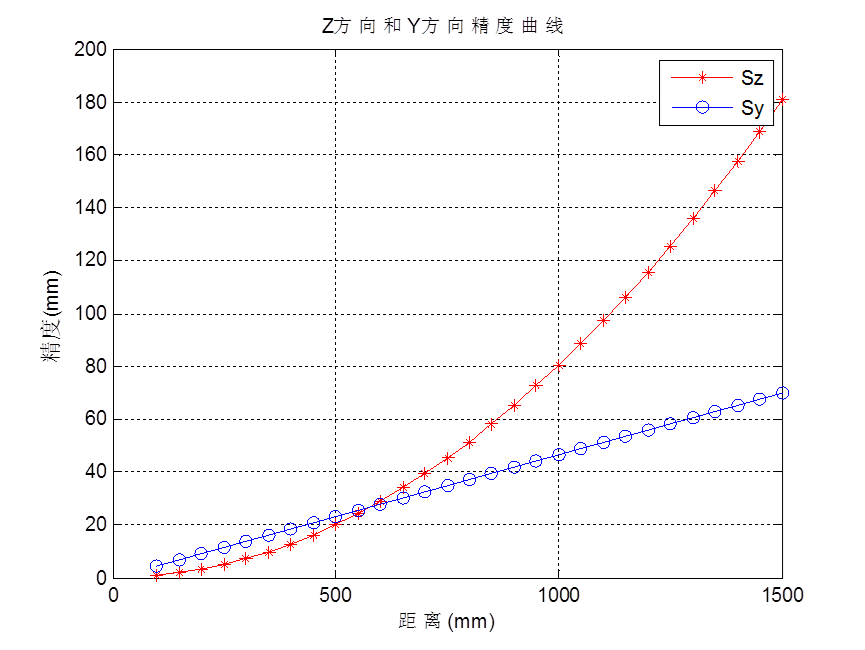
从精度计算的结果和趋势图可以看出，精度数值随着 Z 的增加而变大（意味着精度越来越差），且当 Z 值较大时，
Z方向精度比Y方向精度要差，随着 Z 的增加，差距更加明显。

从仿真数据看，Z方向距离1000mm时，精度值高达80mm，即8%的精度误差。实际上并没有这么大，这与双目立体视觉算法有关。算法的后处理做了子像素拟合，精度为subpix代表的空间大小，因此，实际精度可能只有仿真数据的几分之一。

Y方向的精度不仅跟Z值相关，还跟本身的Y值正相关，Y越大，Y方向的精度越差。