智能反射面文献阅读：基于强化学习的STAR-RIS辅助室内室外通信频谱最大化_基于深度强化学习的智能反射面波束赋形方法研究

最近学习了一篇比较新的2023年的IEEE短文，本篇文献叫做《Deep Reinforcement Learning based Spectral Efficiency Maximization in STAR-RIS-Assisted Indoor Outdoor Communication》，写个博客记录一下，如有错误请大佬纠正。

1. 主要贡献，采取方法，解决问题概述

可重构智能表面(RIS)由于其提高的频谱效率、部署简单性和低成本而在6G中越来越受欢迎。然而，由于传统RIS覆盖范围的局限性，研究方向转向同时发射和反射RIS (STAR-RIS)，在RIS优势的同时提供360度覆盖。这篇文章研究了一种适用于室内外用户的STAR-RIS辅助下行通信系统。然后，提出了在共同控制各用户波束形成功率和STAR-RIS相移值的同时实现频谱效率最大化的优化问题。由于该问题具有np难度，且难以在多项式时间内解决，因此采用了一种用于强化学习的策略梯度方法——近端策略优化(PPO)来解决该问题。为了证明我们提出的算法的有效性，进行了大量的仿真结果。数值结果表明，本文提出的算法优于文献中几种基准方案。
主要贡献：
1.通信模型考虑了在建筑墙上加入STAR-RIS，从而实现室内外的移动用户下行通信系统
2.通过控制每个用户的波束成形功率和STAR-RIS的系数，制定了平均可达速率最大化优化问题。约束条件有基站可用总功率，STAR-RIS所需要考虑的能量守恒定律等。
3.这个优化问题是个NP Hard问题，故采用强化学习的PPO算法解决。
解决问题
提出了在共同控制各用户波束形成功率和STAR-RIS相移值的同时实现频谱效率最大化的优化问题
采取方法
近端策略优化(PPO)

2. STAR-RIS简介，近端策略优化PPO

2.1 STAR-RIS简介

传统的RIS存在局限性。由于RIS仅提供反射功能，当发射端和接收端位于RIS的相对侧时，覆盖范围的扩展受到限制。为了解决这一问题，目前的研究领域正在向同时发射和反射RIS (STAR-RIS)扩展，也称为智能全面表面(IOS)。STAR-RISs将传统的仅反射RISs的优点与每个元件同时传输和反射入射信号的能力相结合，使它们能够克服部署RISs的限制，提供360度覆盖。因此，STAR-RIS可以作为传统RIS系统的改进。基于此，本文研究了STAR-RIS辅助的室内外通信系统，这在以前是传统RIS难以解决的问题，因为用户位于RIS的两侧。

2.2 近端策略优化PPO（Proximal Policy Optimization）

本知识点来自此处BLOG: 【深度强化学习】(6) PPO 模型解析，附Pytorch完整代码
其他PPO介绍博客：
BLOG1: 影响PPO算法性能的10个关键技巧
BLOG2: OpenAI Spinning up
BLOG3: Proximal Policy Optimization (PPO) 算法理解：从策略梯度开始

PPO 算法之所以被提出，根本原因在于Policy Gradient 在处理连续动作空间时 Learning rate 取值抉择困难。Learning rate 取值过小，就会导致深度强化学习收敛性较差，陷入完不成训练的局面，取值过大则导致新旧策略迭代时数据不一致，造成学习波动较大或局部震荡。除此之外，Policy Gradient 因为在线学习的性质，进行迭代策略时原先的采样数据无法被重复利用，每次迭代都需要重新采样；
同样地置信域策略梯度算法（Trust Region Policy Optimization，TRPO）虽然利用重要性采样（Important-sampling）、共轭梯度法求解提升了样本效率、训练速率等，但在处理函数的二阶近似时会面临计算量过大，以及实现过程复杂、兼容性差等缺陷。
PPO 算法具备 Policy Gradient、TRPO 的部分优点，采样数据和使用随机梯度上升方法优化代替目标函数之间交替进行，虽然标准的策略梯度方法对每个数据样本执行一次梯度更新，但 PPO 提出新目标函数，可以实现小批量更新。
鉴于上述问题，该算法在迭代更新时，观察当前策略在 t 时刻智能体处于状态 s 所采取的行为概率，与之前策略所采取行为概率 ，计算概率的比值来控制新策略更新幅度，比值 rt记作：
若新旧策略差异明显且优势函数较大，则适当增加更新幅度；若 rt比值越接近 1，表明新旧策略差异越小。
优势函数代表，在状态 s 下，行为 a 相对于均值的偏差。在论文中，优势函数使用 GAE（generalized advantage estimation）广义优势估计来计算
$${\hat{A}}_t^{GAE\left(\gamma ,\lambda \right)}=\sum _{l=0}^{\infty }{\left(\gamma \lambda \right)}^l{\delta }_{t+l}^V$$
$${\hat{A}}_t^{GAE\left(\gamma ,\lambda \right)}={\delta }_t^V+\left(\gamma \lambda \right){\delta }_{t+1}^V+{\left(\gamma \lambda \right)}^2{\delta }_{t+2}^V+\cdots +{\left(\gamma \lambda \right)}^{T-t+1}{\delta }_{T+1}$$
$${\delta }_t^V=r_t+\gamma V_{\omega }\left(s_{t+1}\right)-V_{\omega }\left(s_t\right)$$

PPO算法本质上是一个On-Policy的算法，它可以对采样到的样本进行多次利用，在一定程度上解决样本利用率低的问题，收到较好的效果。论文里有两种实现方式，一种是含有自适应 KL-散度（KL Penalty）的 PPO-Penalty，另一种是含有 Clippped Surrogate Objective 函数的 PPO-Clip。大部分都是采用的后者。

3. 系统模型与问题建立

这是一个STAR-RIS辅助的室内外下行通信系统，在这篇文章的系统模型当中，考虑有多天线的基站BS，STAR-RIS有N个元素，基站和用户的LOS链路阻碍，室内用户和室外用户与基站之间没有直接链路（Direct link），只有传输链路（Transmitted link）和反射链路（Reflected link)，室内和室外都存在多个用户，且假设每个BS用户位于单独的子载波，即使STAR-RIS反射或者传输了所有入射信号，用户仍能在指定子载波上解码接收到的信号，故BS用户之间不会相互干扰。

3.1 室内和室外通信模型以及传输模型

先简单介绍一下关于信道方面的知识，具体可参考以下博客：
BLOG1: 信道建模（大尺度、小尺度、莱斯衰落、瑞利衰落、莱斯信道、瑞利信道）
BLOG2: 瑞利、莱斯、高斯信道模型
BLOG3: 什么是小尺度衰落信道、瑞利信道、莱斯信道、Nakagami信道

室外通信模型
假设室外既有直接通信也有间接通信，对于直接通信，假设基站与用户不存在LOS链路，故采用瑞利衰落模型（瑞利信道只适用于从发射机到接收机不存在直射信号的情况，也就是说是经过发射、折射或者衍射到达接收机的），故基站与室外用户信道增益表示为：
$${\mathbf{H}}_o=\sqrt{\eta d_o^{-{\beta }_l}}\bar{h}$$

其中为参考距离下的信道增益，为LOS链路路径损耗指数，为基站到室外用户的距离， 为复高斯随机散射元。
对于间接通信链路，也就是经过STAR-RIS反射辅助链路，包含基站到STAR-RIS链路和STAR-RIS到室外用户链路，采用的是莱斯衰落模型（如果收到的信号中除了经反射折射散射等来的信号外， 还有从发射机直接到达接收机的信号，那么总信号的强度服从分布莱斯， 故称为莱斯衰落），基站到STAR-RIS的信道增益为$${\mathbf{h}}_{B,n}=\sqrt{\eta d_{B,n}^{-{\beta }_n}}\sqrt{\frac{R}{1+R}}{\mathbf{h}}_{B,n}^{\text{LoS}}$$
，其中R表示莱斯因子，STAR-RIS到室外用户的反射链路信道增益表示为$${\mathbf{h}}_{n,o}=\sqrt{\eta d_{n,o}^{-{\beta }_n}}\sqrt{\frac{R}{1+R}}{\mathbf{h}}_{n,o}^{\text{LoS}}+\sqrt{\frac{1}{1+R}}{\mathbf{h}}_{n,o}^{\text{NLOS}}$$

室内通信模型
室内通信中，不存在BS到用户的直接通信，只有STAR-RIS的传输链路辅助通信。基站BS到STAR-RIS的信道增益不变，STAR-RIS和室内用户之间的信道增益可表示为$${\mathbf{h}}_{n,i}=\sqrt{\eta d_{n,i}^{-{\beta }_n}}\sqrt{\frac{R}{1+R}}{\mathbf{h}}_{n,i}^{\text{LoS}}+\sqrt{\frac{1}{1+R}}{\mathbf{h}}_{n,i}^{\text{NLOS}}$$

传输模型
任一用户接收到的信号可以表示为（室内和室外均可）：$$y_k^{\nu }=G_k^{\nu }{p}_k{s}_k+{\omega }_k$$
其中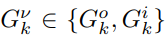表示级联通信信道，室外存在直接通信和间接通信，可表示为，室内只有间接通信。Pk表示波束赋形功率，Sk表示发射信号，wk表示噪声。信噪比（SNR）可以表示为，则根据香农公式可以得到数据速率为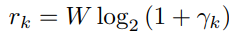

3.2 优化问题建立

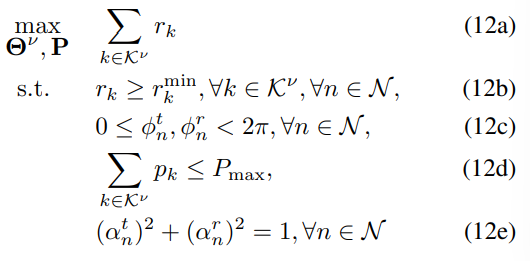
目标就是最大化用户平均可实现数据速率，12b约束表示每个用户速率要至少大于最小速率，约束12c限制相移的值，约束12d表示每个用户分配的波束赋形功率，12e是STAR-RIS特有的约束即能量守恒定理。

4. 解决方案

文章针对这个优化问题很难采用传统的优化方法来解决，所以采用深度强化学习中的近端策划优化（PPO）方法来解决问题。
状态空间
状态空间包含了所有的信道，然后构成相应的元组。用数学形式表示为
s t = { H o , h B , n , h n , o , h n , i , ∀ o ∈ O , ∀ n ∈ N , ∀ i ∈ I } s_t=\{\mathbf{H}_o,\mathbf{h}_{B,n},\mathbf{h}_{n,o},\mathbf{h}_{n,i},\forall o\in \mathcal{O},\forall n\in \mathcal{N},\forall i\in \mathcal{I}\} st​={Ho​,hB,n​,hn,o​,hn,i​,∀o∈O,∀n∈N,∀i∈I}
动作空间
动作空间包含了STAR-RIS传输和反射振幅和相位等参数，用数学形式表示为 a t = { α n ν , ϕ n ν , p k , ν ∈ { o , i } , n ∈ N , k ∈ K ν } a_t=\{\alpha _{n}^{\nu},\phi _{n}^{\nu},p_k,\nu \in \{o,i\},n\in \mathcal{N},k\in \mathcal{K}^{\nu}\} at​={αnν​,ϕnν​,pk​,ν∈{o,i},n∈N,k∈Kν}
注意
转移函数
转移函数定义了环境随着时间而变化，即
奖励函数
奖励函数根据优化目标设定，即最大化所有用户平均可达速率 R t ( s t ∣ a t ) = { − 1 ,    if    ∑ k ∈ K ν r k < r k min ⁡ ∑ k ∈ K ν r k ,    otherwise . \mathcal{R}_t\left( s_t|a_t \right) =

$$\begin{cases} -1,& \,\,\text{if\,\,}\sum_{k\in \mathcal{K}^{\nu}}{r}_k<r_{k}^{\min}\\ \sum_{k\in \mathcal{K}^{\nu}}{r}_k,& \,\,\text{otherwise}.\\ \end{cases}$$ Rt​(st​∣at​)={−1,∑k∈Kν​rk​,​if∑k∈Kν​rk​<rkmin​otherwise.​
PPO算法整体框架图如图所示：

PPO是基于演员评论家的一种算法，在该算法基础上，代理agent在基站BS实现，行动者采用随机策略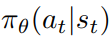，并根据参数θ来学习。智能体从环境感知网络信息作为输入的状态St，策略观察状态并执行动作输出，计算即时奖励，奖励作为反馈给代理，得到新的状态St+1，则t时刻累计折扣奖励函数表示为：$$Q\left(s_t,a_t\right)=\mathbb{E}\left[\sum _{t\in \mathcal{T}}{\tau }_t{\mathcal{R}}_t\left(s_t|a_t\right)\right]$$
根据PPO算法，评论家使用优势函数来估计一个动作相对于给定状态下平均动作执行情况，优势函数定义为$${\ddot{A}}_t=Q\left(s_t,a_t\right)-V_{\mu }\left(s_t\right)$$
（注意，在dueling DQN中有过类似的思想，dueling DQN中有最优优势函数）
采用广义优势估计器GAE可得：$${\ddot{A}}_t={\delta }_t+\left(\tau \lambda \right){\delta }_{t+1}+\cdots +{\left(\tau \lambda \right)}^{T-t+1}{\delta }_{T-1}$$
其中$${\delta }_t={\mathcal{R}}_t\left(s_t|a_t\right)+\tau V_{\mu }\left(s_{t+1}\right)-V_{\mu }\left(s_t\right)$$
损失函数根据TD error可得到$${\mathcal{L}}^V\left(\mu \right)=\mathbb{E}\left[|V_{\mu }^{\text{target}}-V_{\mu }\left(s_t\right)|\right]$$
其中$$V_{\mu }^{\text{target}}={\mathcal{R}}_{t+1}\left(s_{t+1}|a_{t+1}\right)+\tau V_{\mu }\left(s_{t+1}\right)$$
为了决定使整体环境回报最大化的策略可以得到$$\mathcal{L}\left(\theta \right)=\mathbb{E}\left[\min \left({\phi }_t\left(\theta \right){\ddot{A}}_t,clip\left({\phi }_t\left(\theta \right),1-ϵ,1+ϵ\right){\ddot{A}}_t\right)\right]$$
如下所示是整体的伪代码算法框架：

5. 效果评估

如下图所示，对比了STAR-RIS辅助通信模型，传统RIS辅助通信模型，既没有STAR-RIS，也没有RIS辅助通信模型（W/O STAR-RIS），可以看到随着元件数量增加，和速率明显增加，并且提出的STAR-RIS辅助方案优于传统RIS辅助方案。

如下图所示，采用不同的策略的DRL方法，分别是PPO算法，TRPO算法，以及PG算法，从图中可以看出，提出的PPO算法收敛速度比TRPO算法快但是比PG慢，同时比TRPO和PG产生更好的累计奖励。

如下图所示，根据不同的学习率评估PPO算法，学习率分别为0.1，0.001，0.00001，可以看到学习率越高累计奖励越大。然而在较低学习率下，收敛速度减慢。