【抓取】6-DOF GraspNet 论文解读_6-dof graspnetcsdn

【抓取】6-DOF GraspNet 论文解读

【注】：本文地址：【抓取】6-DOF GraspNet 论文解读
若转载请于明显处标明出处。

前言

这篇关于生成抓取姿态的论文出自英伟达。我在读完该篇论文后我简单地对其进行一些概述，如有错误纰漏请指正！

论文概要

生成抓握姿势是机器人物体操纵任务的关键组成部分。 在本工作中，作者提出了抓取生成问题，即使用变分自动编码器对一组抓取进行采样，并利用抓取评估器模型对采样抓取进行评估和微调细化。 抓取采样器和抓取refine网络都以深度相机观察到的三维点云作为输入。 作者评估了在模拟和现实世界机器人实验中的方法。 其方法在具有不同外观、尺度和权重的各种常用对象上获得88%的成功率。 作者直接在模拟环境中训练而在现实场景下进行实验测试，这其中没有任何额外的步骤。

整体网络概述

整体网络结构如下图：

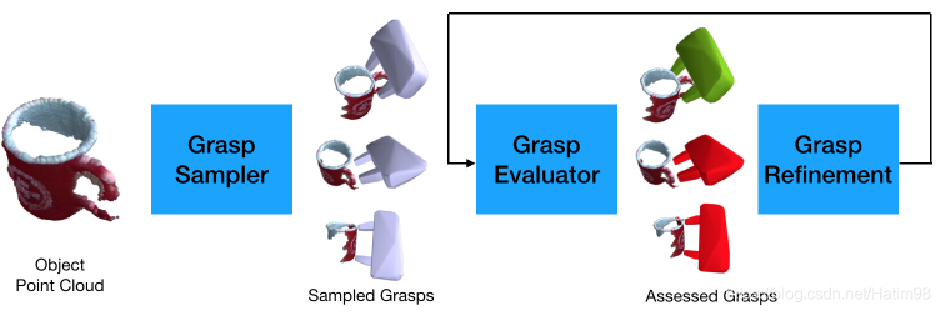
首先，输入三维点云，通过 Grasp Sampler 也就是抓取采样网络，得到多个抓取；然后通过一个 Grasp Evaluater ，评估上一步生成的抓取的成功与否；在评估这一步中，通过 Grasp Refinement 将估计的抓取结果进行微调，使其更贴近于合理抓取，进一步地增大了抓取的成功率。

下面具体来讲一下每一部分。

Variational Grasp Sampler

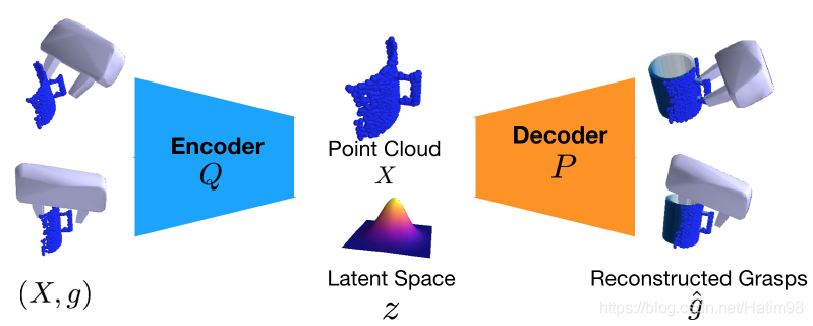
抓取采样网络本质上是一个VAE，也就是变分自编码器。输入 $X$ 是对原始目标三维点云采样得到的各个视角下的目标点云， $g$ 其实就是抓取姿态，也就是抓取器在目标坐标系下的 $R$ 和 $T$。通过VAE的编码器Q，将输入编码到隐层空间，得到低维度的隐层变量 $z$ ，使其满足单位高斯分布；然后再通过对隐层变量 $z$ 解码，得到与输入相近的 $g$ 。整个VAE的训练过程就是让z尽量服从上面所说的单位高斯分布，所以在测试的时候，去掉Encoder，直接在单位高斯分布中随机取样，取代了需要编码得到的隐层变量 $z$ ，再加上输入点云 $X$ ，就可以得到网络所认为的绝对正确的重建抓取 $\hat{g}$ 。在训练中，VAE的损失函数如下：
$${\mathcal{L}}_{\mathrm{v}\mathrm{a}\mathrm{e}}=\sum _{z\sim Q,g\sim G^{\ast }}\mathcal{L}(\hat{g},g)-\alpha {\mathcal{D}}_{KL}[Q(z\mid X,g),\mathcal{N}(0,I)]$$
该式采用随机梯度下降优化。 对于每个mini-batch，点云 $X$ 从随机视点观察采样。 对于采样点云 $X$ ，抓取 $g$ 从Ground Truth集合$G^{\ast }$采用分层采样。
上式中的 $\mathcal{L}(g,\hat{g})$ 具体式子如下：
$$\mathcal{L}(g,\hat{g})=\frac{1}{n}\sum \Vert \mathcal{T}(g;p)-\mathcal{T}(\hat{g};p){\Vert }_1$$
此式约束重建抓取与输入抓取相近。 $\mathcal{T}(\cdot ;p)$ 是机器人夹持器上一组预定义点 $p$ 的变换，什么意思呢？换句话说就是，在目标坐标系中，把抓取器的模型通过 $R$ 和 $T$ 作变换，从而转变为目标坐标系下的抓取器点云。

Grasp Pose Evaluation

因为前一步生成的抓取在网络看来他一定是正确的（因为他认为自己的 $z$ 服从单位高斯分布，那么从单位高斯分布中取样重建出的 $\hat{g}$ 一定是正确的抓取），所以实际上要想知道生成的抓取在我们看来是否可行，就还需要加一个判断。因此作者在抓取采样网络之后加了个抓取姿态评估网络。

整个评估网络实质上是一个二分类网络，输入是目标和抓取器的合成渲染点云 $X\cup X_g$ ，输出是成功率 $s$ 。利用交叉熵损失优化抓取评价网络：
$${\mathcal{L}}_{\text{evaluator }}=-(y\log (s)+(1-y)\log (1-s))$$
式中 $y$ 是抓取的Ground Truth二进制标签，1/0 代表 成功/失败。

在训练中采取了hard negative mining（有翻译叫他难负例挖掘），简单俩说就是建立了一个错题集 $G^{-}$ ：
$$G^{-}=\left\{g^{-}\mid \exists g\in G^{\ast }:\mathcal{L}\left(g,g^{-}\right)<ϵ\right\}$$
在训练过程中，这个错题集中包含：

1. 从一组预先生成的负抓取中采样 $g^{-}$ ;
2. 或者通过随机扰动正抓取集 $G^{\ast }$ 中的 $g$ 使夹持器的网格要么与物体网格碰撞，要么将夹持器网格远离物体。

Iterative Grasp Pose Refinement

前面说完了，这一部分我觉得才是重点部分！通过前面的评估，已经得到了一些成功和失败的抓取例子，那么怎么提高成功率呢？换句话说，怎么让估计出来的抓取 $g$ 更好呢？

为了达到这个目的，作者想到了一个巧妙的办法，既然评估网络中的 $s$ 越大代表越可能成功，那么使得这些 $s$ 都尽可能地变大并且趋近于1也就能让抓取 $g$ 更好了呗~

实际上这就代表了能让 $s$ 相对于 $g$ 的函数 $S$ 值变大的方向。这个方向就是 $S$ 相对于 $g$ 的梯度方向，也就得到了下面的式子：
$$\Delta g=\frac{\partial S}{\partial g}=\eta \times \frac{\partial S}{\partial \mathcal{T}(g;p)}\times \frac{\partial \mathcal{T}(g;p)}{\partial g}$$

如果上面不理解，也没关系，有点绕口。我说一个一维曲线的例子。
如上图所示，$y=f(\theta x)$ 代表拟合出来的曲线，其中 $\theta$ 代表 $x$ 的系数（等同于网络的权重参数）。现在假如输入是 $x_1$ ，输出是 $y_1$，然后我已知 $y_2$ 是一个更好更大的输出值，那么我就需要改变 $x$ 的值，让 $x_1$ 变成 $x_2$ ：
$$x_2=x_1+\Delta x$$
那么变化量 $\Delta x$ 怎么得到呢？在这个例子里， $x$ 变化无非两种情况，要么变大要么变小，要想知道我们需要他变大还是变小，只需要让函数 $f$ 对 $x$ 求导就得到了斜率，斜率就指明了 $x$ 变化方向。在这个例子里面 $x$ 变化方向是 $x$ 轴的正方向。得到了变化方向我们乘上一个步长 $\eta$ 就得到了我们需要的变化量 $\Delta x$ ：
$$\frac{\partial f}{\partial x}\cdot \eta =\Delta x$$

Experiments

实验部分暂时不说了，作者说这抓取效果就是好反正。其他自对比实验也很有意义，有空再更。