devbox
知新_RL
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

Unity游戏开发客户端面经——算法（初级）_unity 游戏前端常用算法

作者：知新_RL | 2024-02-26 19:39:41

赞

踩

unity 游戏前端常用算法

前言：记录了总6w字的面经知识点，文章中的知识点若想深入了解，可以点击链接学习。由于文本太多，按类型分开。这一篇是 算法 常问问题总结，有帮助的可以收藏。

1.十大排序

 

        时间复杂度：O(n²)        ：冒泡排序、选择排序、插入排序

                             O(nlogn)   :堆排序、快速排序、（归并排序）

        不稳定的排序：选择排序、快速排序、堆排序、希尔排序。

        详细请看： （强烈推荐）https://leetcode.cn/circle/discuss/eBo9UB/#https://leetcode.cn/circle/discuss/eBo9UB/

        若基本有序建议用插入排序，不建议用快速排序。

2. 100万的数据选出前1万大的数

        利用堆排序、小顶堆实现。 

        先拿10000个数建堆，然后一次添加剩余元素，如果大于堆顶的数（10000中最小的），将这个数替换堆顶，并调整结构使之仍然是一个最小堆，这样遍历完后，堆中的10000个数就是所需的最大的10000个。建堆时间复杂度是O（mlogm），算法的时间复杂度为O (nmlogm)（n为100，m为10000）。

        优化的方法：分治。可以把所有10亿个数据分组存放，比如分别放在1000个文件中。这样处理就可以分别在每个文件的10^6个数据中找出最大的10000个数，合并到一起在再找出1000*10000中的最终的结果。

3. 两个10G 的文件，200m 内存，排序

        1.把 10G 大小的文件拆分成 N 个小文件，每个文件 1M 。

        2.把每个文件拉倒内存排序，可以并行操作，在内存中直接使用快排，然后写入文件 。

        3.对文件做两两合并。

4. A星算法

     1.基本原理

        避障碍寻路算法有很多，比如：BFS，DFS，Dijkstra等。

        对于BFS，它的优点在于可以找到最优的一条路径，缺点是需要遍历整个地图。

        对于DFS，它的优点在于不需要遍历整个地图，缺点在于不一定是最优路径。

        对于Dijkstar，它的优点在于无差别的遍历当前最短路径，对于查找起始点到任意点的最短路径该算法很有效，缺点是：对于点对点的路径查找很浪费。

        对于A*，它能很快的找到一条相对最优的路径，而且搜索的节点比前三个算法都要少。

        如果DFS就像一个愣头青，一条路摸到黑的话，那么A*就是一个聪明的愣头青，它虽然也是一条路摸到黑，但是它每一步都会更加逼近终点，而不是像DFS每一步都是随机的。可以理解为A*吸收了DFS和BFS的优点，寻找到的路径优劣程度介于BFS和DFS之间。

        简单的说，A*算法就是不停的从起点开始遍历周围的点，找出目前来说消耗最小的点作为新的起点，直到找到终点。

     2. 如何找到消耗最小的点

        1.F（总代价，走到终点消耗得代价）=G（该点离起点距离）+H（该点离终点距离）。

        2.G：从起点到达当前点要走的距离，上下左右都是1，斜边用勾股定理算出约为1.4。

        3.H:按照曼哈顿距离计算（d(i,j)=|X1-X2|+|Y1-Y2| ）。

        4.开启列表open：用来存储可以考虑行进的点，同时存放F、G、H、父对象（从哪个点来）的信息。

        5.关闭列表close：用来存储不再考虑的点，存放在关闭列表中的点需要从开启列表移除，同时存放F、G、H、父对象（从哪个点来）的信息。

     3. 如何确定路径

        1.虽然最优点都在关闭列表中，但是并不能直接使用关闭列表中的点作为路径。

        2.而是在关闭列表中从终点开始查找父对象，再查找父对象的父对象。

        3.死路：当开启列表为空的时候，说明已经找遍了所有可能的点，寻路失败。

     4.  详细流程

        1、将起点记录为当前点a。

        2、将当前点a放入关闭列表close，并设置父对象为空。

        3、将当前点a周围所有能行进的格子放入开启列表，如果周围的点已经在开启列表或者关闭列表中再或者是障碍，就不用管它了。

        4、记录当前点a周围所有能行进的格子的F值和父对象（父对象为当前点）。

        5、重新在open列表中寻找最优点b（F最小值）将其放入关闭列表，同时在开启列表中移除，每次往关闭列表放点时，要判断该点是否为终点，如果是证明路径已经找完了，结束寻路，如果不是则继续

        6、将最优点作为起点b

        7、重复上述3、4、5、6步骤，直到找到终点。

        8、找到终点，寻路结束，根据终点得父节点返回到起点，为最优路径。

        原文链接：读书|杂谈|技术分享-我的编程学习笔记一个分享读书笔记,个人杂谈,技术资源的博客网站https://www.lengyueling.cn/archives/33

        A星基础：

A星算法_筱的博客-CSDN博客_a星算法A星算法1.简述A星算法就是试图在地图中找到一条最短路径，但不保证一定存在。任务小猫去找青蛙玩（好TM弱智啊~）条件黑色方块无法通行，每走一个格子小猫消耗的体力都为1。2.如果说你是小猫，你会怎么走？嗯，毫无疑问你肯定这么走。。。很简单的对吧，但是你这么走的时候，真的没经过思考？并非如此吧，你要找最短路径是不是直接连线是最快的？但是连线有障碍物阻挡了，所以逼迫你先往上走出障碍物的区域，然后一路直线当然就是最短路径了。BUT，你所做的思考，都是建立在你脑海里已经有整张地图的概念上，代https://blog.csdn.net/cqs123111/article/details/115303885

        A星进阶：

全网最全A*算法优化策略（JPS、HPA）_Wonder-King的博客-CSDN博客_a*算法优化A*算法（A-Star）是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快，是最常用的启发式算法。避障碍寻路算法有很多，比如：BFS，DFS，Dijkstra等。对于BFS，它的优点在于可以找到最优的一条路径，缺点是需要遍历整个地图。对于DFS，它的优点在于不需要遍历整个地图，缺点在于不一定是最优路径。https://blog.csdn.net/qq_42391248/article/details/119727974

        优缺点

        A*算法优点在于对环境反应迅速，搜索路径直接，是一种直接的搜索算法，因此被广泛应用于路径规划问题。

        其缺点是实时性差，每一节点计算量大、运算时间长，而且随着节点数的增多，算法搜索效率降低。

     5.  A*优化？

        1.找到用更合适的OpenList数据结构。

        2.在openlist列表用list容器存储，遍历f最小节点元素时间复杂度为O（n），可以用二叉堆实现openlist，获取f最小的节点只需要将堆顶元素拿出来然后使堆重新成为一个二叉堆即可，复杂度是O(lngN)。

        3.在f相同的时候，选取h小的节点，减少遍历次数。

        4.预先分配必要的内存。

        5.缓存和一个节点相邻的节点，因为 A* 需要频繁获取某个节点相邻节点的操作。

        6.由计算该节点的4个邻居改为8个邻居等（横向扩展）。

        7.如果你想让A*看的更远，可以在扩大A*眼界范围，也可以是周围两圈，三圈等等。当然，眼界越大，就意味着A*要计算的节点也就越多，A*的速度一定会变慢，优点是可以让A*找到更优的路径。

        详细请看：【游戏AI-寻路】优化A*的几种方法 - 知乎A*算法在说怎么优化 A* 前，先复习一下A* 算法的基本过程，算法过程可以用下面的伪代码描述： // 初始化起点的信息 pn = pathNodes[startNode.NodeIndex]; pn.parent = startNode; pn.h = CalculateH(); pn.g = 0;…https://zhuanlan.zhihu.com/p/489189483

全网最全A*算法优化策略（JPS、HPA）_Wonder-King的博客-CSDN博客_a*算法优化A*算法（A-Star）是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快，是最常用的启发式算法。避障碍寻路算法有很多，比如：BFS，DFS，Dijkstra等。对于BFS，它的优点在于可以找到最优的一条路径，缺点是需要遍历整个地图。对于DFS，它的优点在于不需要遍历整个地图，缺点在于不一定是最优路径。https://blog.csdn.net/qq_42391248/article/details/119727974

     6. A*如何减少斜线两点间的摆头（优化重要点！！）

        拉绳算法！

        拉绳算法/漏斗算法：即从起点开始，与路径网格的临边的点进行相连，然后依次移动左边界和右边界，判断移动后的夹角变换，如果夹角变小了，说明离终点更近了，合理；继续；如果夹角变大了，说明离终点更远了；则选择另一个边界移动；如果同样变大，则需要进行路径合并了，选择当前边界上的点作为新的起点，并与旧起点相连得到一条路径；从新起点开始刚刚的操作，直到到达终点；

        详细请看：Navigation Mesh (NavMesh) 原理讲解（二） 当地块都是三角形时的路径优化 - 知乎上篇讲到NavMesh在找到路径后，由于路径沿地块（网格）中心点连接，因此通常还有优化空间，可以尝试缩短路程。本篇中，将介绍一种如果每个地块都是三角形的情况下进行路径优化的方法。毕竟三角形作为最简单的几何…https://zhuanlan.zhihu.com/p/359393767

5. 快速幂算法

        数学公式：Math.Pow(m, n)  【m的n次方】

        讲解：利用公式  ,可以直接用底数的平方，指数除以2的方式，这样指数降到0只需要 log(n) 次 ，因此 时间复杂度 仅需要 O(log n) 比朴素的模拟乘方法 O(n) 优秀的多。

        递归算法

        非递归算法

        详细请看：

数据结构与算法：快速幂——求幂运算 O(logN)_正在奋斗中的小志的博客-CSDN博客_数据结构logn快速幂——求幂运算 O(logN)https://blog.csdn.net/Sea3752/article/details/124576488?spm=1001.2014.3001.5502

6. 二分查找

        二分模板一共有两个，分别适用于不同情况。

        算法思路：假设目标值在闭区间[l, r]中，每次将区间长度缩小一半，当l = r时，我们就找到了目标值。

        1.当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1。(常用)       

        2.当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。

        3.代码里的if语句，若变成一个bool函数带入对应的l，r，mid，array等，在函数里面继续二分查找，即可变成“二分答案”。

7. BFS（广度优先搜索）

        BFS从根节点开始搜索，并根据树级别模式探索所有邻居根。它使用队列数据结构来记住下一个节点访问。

        1.如果不需要确定当前遍历到了哪一层

         2.如果要确定当前遍历到了哪一层，BFS 模板如下。 这里增加了 level 表示当前遍历到二叉树中的哪一层了，也可以理解为在一个图中，现在已经走了多少步了。size 表示在当前遍历层有多少个元素，也就是队列中的元素数，我们把这些元素一次性遍历完，即把当前层的所有元素都向外走了一步。

8. DFS（深度优先搜索）

        注意搜索的顺序；当搜到叶子节点（递归结束）时就回溯，回退一步看一步。

        DFS从根节点开始搜索，并从根节点尽可能远地探索这些节点。使用堆栈数据结构来记住下一个节点访问。

        类似于树的 先序遍历

        模板：

        详细请看：深度优先搜索与广度优先搜索的本质区别！ - 知乎最近在看数据结构中图的相关知识，之前看的很混乱，现在总算是理清了，在此记录一下。 目录： 图的基本知识广度优先搜索（BFS）深度优先搜索（DFS）总结代码实现 一、图的基本知识 日常有很多地方都用到了图，比如…https://zhuanlan.zhihu.com/p/74472146?ivk_sa=1024320u

9. 欧拉筛（解决素数）

        详细请看：

数据结构与算法：欧拉筛——查找素数（质数）的最优解算法 O(n)_正在奋斗中的小志的博客-CSDN博客_什么算法最优时是o(n)欧拉筛——查找素数（质数）的最优解算法https://blog.csdn.net/Sea3752/article/details/124572498?spm=1001.2014.3001.5502

10. 斐波拉契数列

         0、1、1、2、3、5、8、13、21....

        递归：

  1.  Int fib (n) {
  2.  
  3.      if(n==0) return 0;
  4.  
  5.      if(n==1) return 1;
  6.  
  7.      if(n>=2){
  8.  
  9.          res= (fib(n-1)+fib(n-2))%(1e9+7);
  10.  
  11.      }
  12.  
  13.      return res;
  14.  
  15. };

        循环

        最优解：矩阵快速幂（longn）

        详细请看：

力扣https://leetcode.cn/problems/fei-bo-na-qi-shu-lie-lcof/solution/kuai-su-mi-ju-zhen-kuai-su-mi-bi-ji-by-e-fvt9/

力扣https://leetcode.cn/problems/fei-bo-na-qi-shu-lie-lcof/solution/gong-shui-san-xie-yi-ti-si-jie-dong-tai-9zip0/

11. 背包问题

        dp定义

        对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

        1.  01背包

        先遍历物品

  1. // weight数组的大小 就是物品个数
  2.  
  3. for(int i = 1; i < weight.size(); i++) { // 遍历物品
  4.  
  5.     for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
  6.  
  7.         if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 这个是为了展现dp数组里元素的变化
  8.  
  9.         else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);        
  10.  
  11.     }
  12.  
  13. }

        

        先遍历背包

  1. // weight数组的大小 就是物品个数
  2.  
  3. for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
  4.  
  5.     for(int i = 1; i < weight.size(); i++) { // 遍历物品
  6.  
  7.         if (j < weight[i]) dp[i][j] = dp[i - 1][j];
  8.  
  9.         else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
  10.  
  11.     }
  12.  
  13. }

        优化：一维（倒着遍历防止被重复放入）

  1.   for(int i = 0; i < weight.size(); i++) { // 遍历物品
  2.  
  3.         for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
  4.  
  5.             dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
  6.  
  7.         }
  8.  
  9. }

        

        详细请看：动态规划：关于01背包问题，你该了解这些！01背包它来了，它迈着整齐的步伐走来了！https://mp.weixin.qq.com/s/FwIiPPmR18_AJO5eiidT6w

        2. 完全背包

        算法由来：有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

        例题：

        给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

        给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。

        完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

        示例 1： 输入：n = 12 输出：3 解释：12 = 4 + 4 + 4

        示例 2： 输入：n = 13 输出：2 解释：13 = 4 + 9

        提示：

        1 <= n <= 10^4

        核心代码：

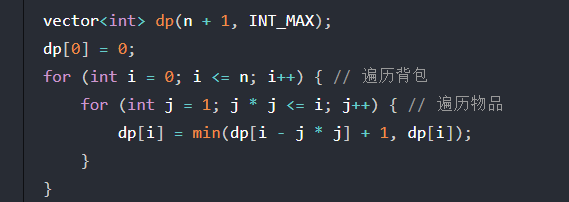
        整体代码：

  1. class Solution {
  2.  
  3.     // 版本一，先遍历物品, 再遍历背包
  4.  
  5.     public int numSquares(int n) {
  6.  
  7.         int max = Integer.MAX_VALUE;
  8.  
  9.         int[] dp = new int[n + 1];
  10.  
  11.         //初始化
  12.  
  13.         for (int j = 0; j <= n; j++) {
  14.  
  15.             dp[j] = max;
  16.  
  17.         }
  18.  
  19.         //当和为0时，组合的个数为0
  20.  
  21.         dp[0] = 0;
  22.  
  23.         // 遍历物品
  24.  
  25.         for (int i = 1; i * i <= n; i++) {
  26.  
  27.             // 遍历背包
  28.  
  29.             for (int j = i * i; j <= n; j++) {
  30.  
  31.                 if (dp[j - i * i] != max) {
  32.  
  33.                     dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
  34.  
  35.                 }
  36.  
  37.             }
  38.  
  39.         }
  40.  
  41.         return dp[n];
  42.  
  43.     }}
  44.  
  45. class Solution {
  46.  
  47.     // 版本二， 先遍历背包, 再遍历物品
  48.  
  49.     public int numSquares(int n) {
  50.  
  51.         int max = Integer.MAX_VALUE;
  52.  
  53.         int[] dp = new int[n + 1];
  54.  
  55.         // 初始化
  56.  
  57.         for (int j = 0; j <= n; j++) {
  58.  
  59.             dp[j] = max;
  60.  
  61.         }
  62.  
  63.         // 当和为0时，组合的个数为0
  64.  
  65.         dp[0] = 0;
  66.  
  67.         // 遍历背包
  68.  
  69.         for (int j = 1; j <= n; j++) {
  70.  
  71.             // 遍历物品
  72.  
  73.             for (int i = 1; i * i <= j; i++) {
  74.  
  75.                 dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
  76.  
  77.             }
  78.  
  79.         }
  80.  
  81.         return dp[n];
  82.  
  83.     }}

        详细请看：

https://programmercarl.com/背包问题理论基础完全背包.html#完全背包https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85.html#%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85

        背包问题优秀总结（推荐）：

https://github.com/youngyangyang04/leetcode-master/blob/master/problems/背包总结篇.mdhttps://github.com/youngyangyang04/leetcode-master/blob/master/problems/%E8%83%8C%E5%8C%85%E6%80%BB%E7%BB%93%E7%AF%87.md

12. 双指针

1 定义

        顾名思义，双指针即用两个不同速度或不同方向的指针对数组或对象进行访问，通过两个不同指针的碰撞从而达到特定的目的。

        2 解决问题

        在时间或空间条件有限的情况下使用单向遍历需要消耗大量的时间或者根本无法解决问题，这时候就需要我们使用双指针，通过指针的碰撞判断是否达到条件，从而解决问题。

        双指针分为快慢指针和左右指针，左右指针通常在数组有序的情况下使用，快慢指针通常在单向遍历需要消耗大量时间，或者有特定要求限制的情况下使用。

        3 经典例题

        接雨水：力扣https://leetcode.cn/problems/trapping-rain-water/

        解法，获取左右指针，循环条件即遍历完所有数组即可完成，所以时间复杂度为O(n),循环进行条件：l<r;每次循环时，找到左右墙的最大值，以此遍历即可。代码：

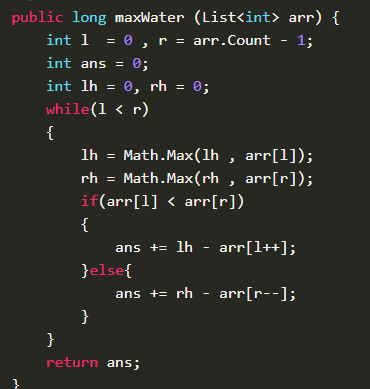
13. 最长递增子序列

        给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

        原地址：

力扣https://leetcode.cn/problems/longest-increasing-subsequence/

        子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

        示例 1：

        输入：nums = [10,9,2,5,3,7,101,18]

        输出：4

        解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

        示例 2：

        输入：nums = [0,1,0,3,2,3]

        输出：4

        示例 3：

        输入：nums = [7,7,7,7,7,7,7]

        输出：1

        代码：（动态规划+二分查找  时间复杂度O(nlongn) ）

        转移方程： 设 res 为 tails 当前长度，代表直到当前的最长上升子序列长度。设 j∈[0,res)，考虑每轮遍历 nums[k]时，通过二分法遍历 [0,res)列表区间，找出 nums[k] 的大小分界点，会出现两种情况：

        区间中存在 tails[i] > nums[k]： 将第一个满足 tails[i] > nums[k] 执行 tails[i] = nums[k] ；因为更小的 nums[k] 后更可能接一个比它大的数字（前面分析过）。

        区间中不存在 tails[i] > nums[k]： 意味着 nums[k]可以接在前面所有长度的子序列之后，因此肯定是接到最长的后面（长度为 resres ），新子序列长度为 res + 1。

14. 查并集

        核心思想“我朋友的朋友就是我的朋友”

        核心代码

        详细地址：

查并集及优化___Hiro__的博客-CSDN博客基础对于今天要总结的算法，我想先通过一道题目来看一下：假设现在我有一个任务交给你：要求你查看 id 为 x 和 id 为 y 的两个人是不是朋友，在一开始我会在第一行中输入 3 个数字 n、m 、k。n 是代表总人数。接下来 m 行，每一行我会输入两个数字： Xi 、 Yi， 代表 id 为 Xi 和 id 为 Yi 的两个人是朋友（注意：朋友的朋友也是朋友）， 接下来 k 行...https://blog.csdn.net/Hacker_ZhiDian/article/details/60965556?spm=1001.2014.3001.5506

15. 敏感词匹配

        1.如果不考虑性能的话，建立一个“敏感词”语句库，利用constains和replace操作直接替换，不过时间复杂度比较高。

        2.AC自动机

        1）构建Trie树（字典树，前缀树）

        从根节点出发，可以向后无限延伸，每个节点都有多个子节点，将敏感词的每一个字拆分开，作为一个节点，以特定的顺序排列，来构建成一个Tire树。

        2）构建Fail指针（失配指针）

        在检索Trie树的时候，在某个分支的节点上匹配失败，可以重新指向关联的其他分支上，避免了从头开始冗余检索。

        构建树的过程中，将每一个敏感词拆分开，以此向下构建，当构建完成后，标记一个敏感词长度，用于回溯。当敏感词有重复的节点时，将重复的敏感字作为父节点，不同的依次向下构建。

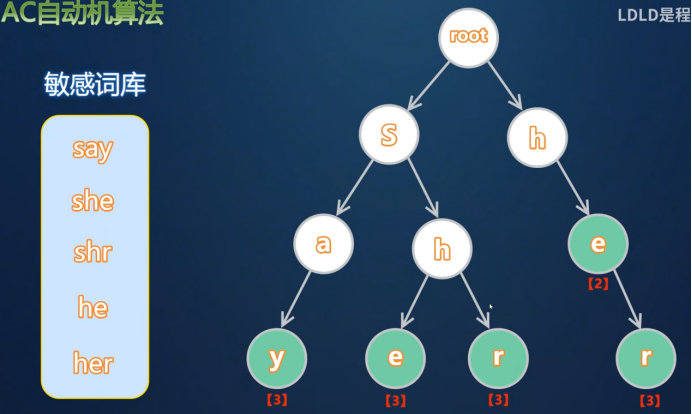
        构建Fail指针过程中

        一、构建fail指针的遍历为层次遍历。

        二、root节点的fail指针指向自己本身。

        三、如果当前节点父节点的fail指针指向的节点下存在与当前节点一样的子节点，则当前节点的fail指针指向该子节点。否则指向root节点。

        

        若遍历语句的时候，到达“结束节点”时，根据当前结束节点标记的“length”来进行回溯，找到包含的敏感词，当语句没有结束时，但已经到了“结束节点”，就根据Fail指针，指向另一个节点继续遍历。直到将语句中所有的字遍历检查完成即可找出所有所有的“敏感词”。所以时间复杂度为O（n）。

        详细请看（bilibil）：

【全程干货】程序员必备算法！AC自动机算法敏感词匹配算法！动画演示讲解，看完轻松掌握，面试官都被你唬住！！_哔哩哔哩_bilibili程序员必备算法！敏感词匹配算法AC自动机算法，详细讲解了AC自动机的构建，包括Trie树构建，fail指针构建。up对剪辑还不太熟悉，请大家多多包含，呕心之作，喜欢的观众希望一键三连，求关注，求关注，求关注！！！祝您生活愉快！！！, 视频播放量 482、弹幕量 1、点赞数 34、投硬币枚数 16、收藏人数 32、转发人数 7, 视频作者 LDLD是程序猿, 作者简介 交个朋友吧，我的vx：17765291517，相关视频：【游戏开发教程】各类迷宫自动生成算法详解 - 游戏算法全系列地形篇（持续更新中），你觉得自己这辈子都学不会编程？超超超基础Python课程，120分钟快速入门 【自学Python教程合集】，[算法]轻松掌握ac自动机，最浅显易懂的 KMP 算法讲解，【零基础 快速学Java】韩顺平 零基础30天学会Java，10分钟彻底搞懂“动态规划”算法，[算法]轻松掌握ac自动机_5_code实现，「一个模型」教你搞定贝叶斯和全概率公式，SEO快速排名算法之一：匹配算法，AC自动机详解&演示https://www.bilibili.com/video/BV1Ag41117YU/?spm_id_from=333.337.search-card.all.click&vd_source=a0e1a6c98f31da08ec684b90c3d4c2cc

16.一个数组的值将其顺序打乱

        设置随机取两个下标进行交换，可以进行双指针随机取值，交换一定的数量达到打乱的效果。

        希望此篇文章可以帮助到更多的同学，此外对现在面临校招的大三大四的同学，以及热爱游戏或者即将面临找工作的朋友，可以点击下方链接，来解决游戏职业道路的种种困惑，并且还可以学习理论知识的同时，拓宽游戏制作的实践技能~

游戏行业大揭秘icon-default.png?t=N2N8https://scrm.vipskill.com/CMS/prod/5726/54/home.html?mantisSiteId=175&track_id=__TRACKID__

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/知新_RL/article/detail/146388
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号