[深度学习] DeepFM 介绍与Pytorch代码解释_deepfm pytorch

一. DeepFM算法的提出

由于DeepFM算法有效的结合了因子分解机与神经网络在特征学习中的优点：同时提取到低阶组合特征与高阶组合特征，所以越来越被广泛使用。

在DeepFM中

• FM算法负责对一阶特征以及由一阶特征两两组合而成的二阶特征进行特征的提取
• DNN算法负责对由输入的一阶特征进行全连接等操作形成的高阶特征进行特征的提取

具有以下特点：

1. 结合了广度和深度模型的优点，联合训练FM模型和DNN模型，同时学习低阶特征组合和高阶特征组合。
2. 端到端模型，无需特征工程。
3. DeepFM 共享相同的输入和 embedding vector，训练更高效。
4. 评估模型时，用到了一个新的指标“Gini Normalization”

二. DeepFM算法结构图

算法整体结构图如下所示：

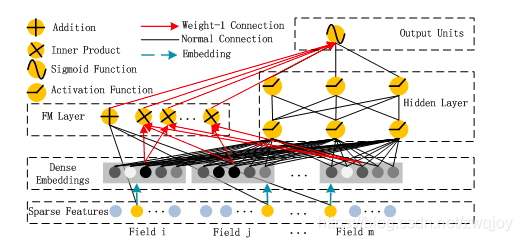
DeepFM的输入可由连续型变量和类别型变量共同组成，且类别型变量需要进行One-Hot编码。而正由于One-Hot编码，导致了输入特征变得高维且稀疏。应对的措施是：针对高维稀疏的输入特征，采用Word2Vec的词嵌入（WordEmbedding）思想，把高维稀疏的向量映射到相对低维且向量元素都不为零的空间向量中。

DeepFM包含两部分：因子分解机部分与神经网络部分，分别负责低阶特征的提取和高阶特征的提取。这两部分共享同样的嵌入层输入。DeepFM的预测结果可以写为：

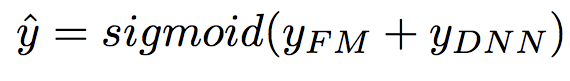
通过嵌入层，尽管不同field的长度不同（不同离散变量的取值个数可能不同），但是embedding之后向量的长度均为K（我们提前设定好的embedding-size)。

DeepFM的各模块共享同一输入，输入是由各个field的Onehot编码横向拼接而成的高维稀疏向量。

首先，原始输入的各个field经过加权（实际上是Embedding为1维）后，求和可得一次项；

其次，原始输入的各个field（不同长度）的Embedding（等长，k维latent vector），一方面两两内积，然后求和可得二次项，另一方面作为输入全连接到DNN。

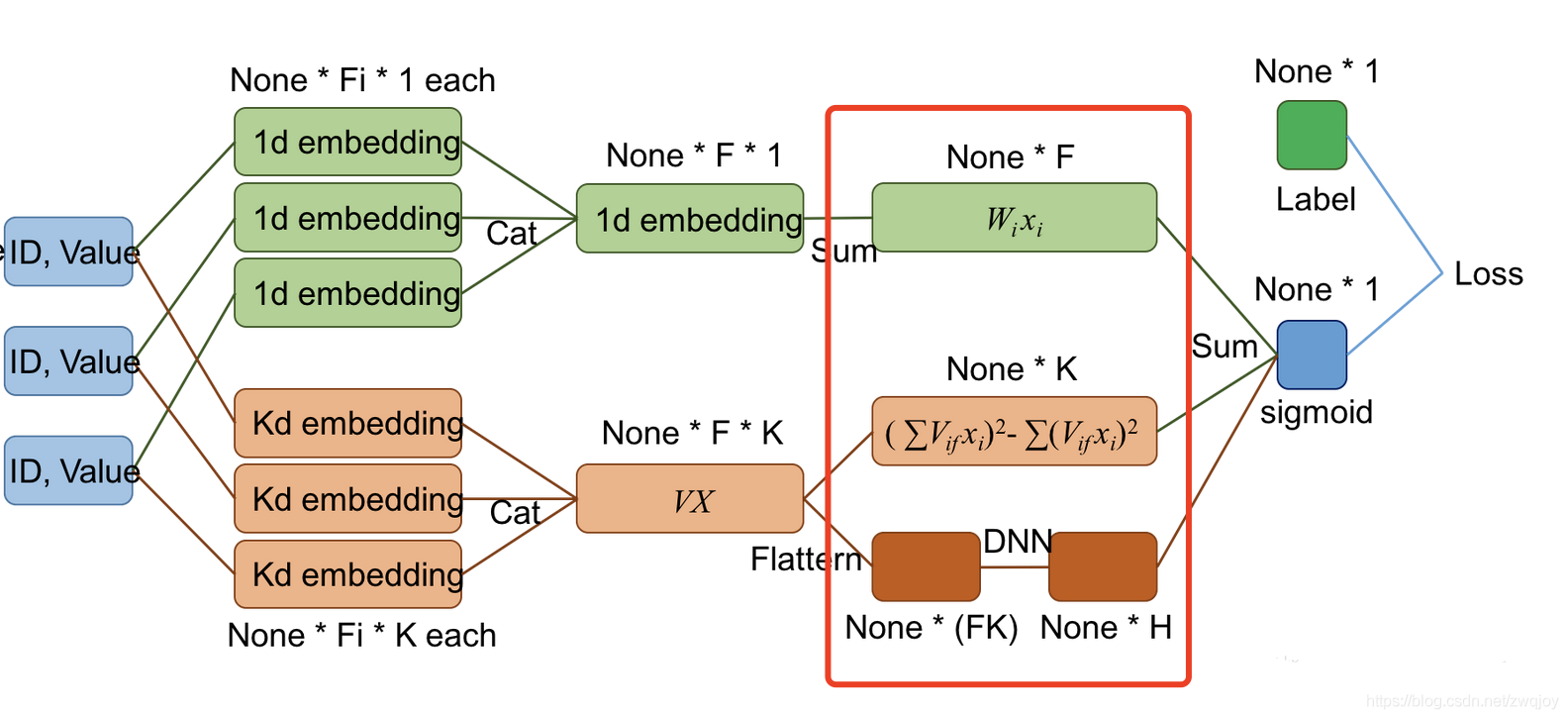
算法整体结构图来源于paper原文，看起来比较复杂。那看一下网友的简略图：

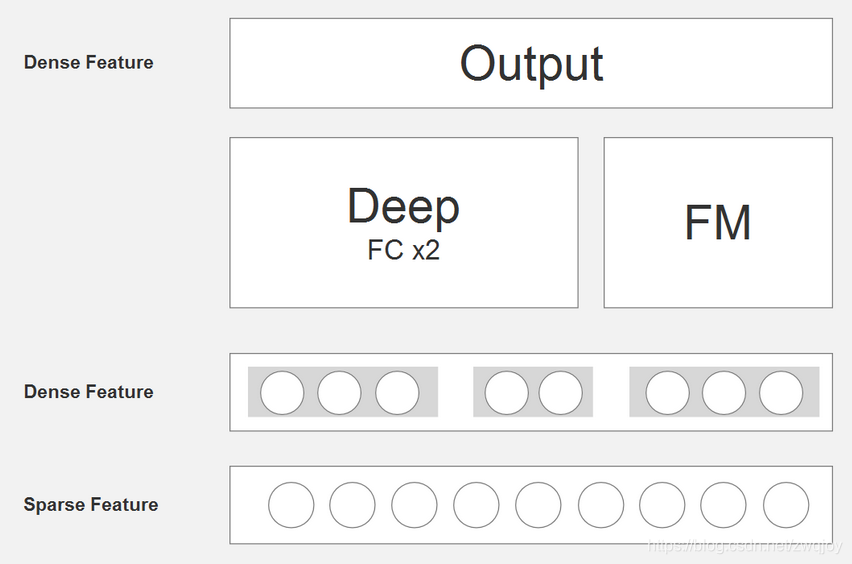
FM部分的结构：

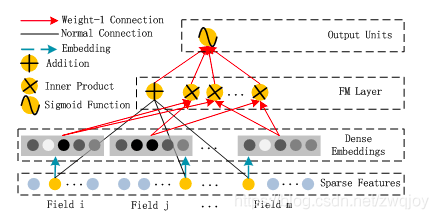
FM 部分的输出如下：

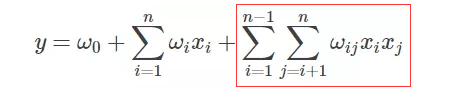
这里需要注意三点：

1. 这里的wij，也就是<vi,vj>，可以理解为DeepFM结构中计算embedding vector的权矩阵（看到网上很多文章是把vi认为是embedding vector，但仔细分析代码，就会发现这种观点是不正确的）。
2. 由于输入特征one-hot编码，所以embedding vector也就是输入层到Dense Embeddings层的权重
3. Dense Embeddings层的神经元个数是由embedding vector和field_size共同确定，再直白一点就是：神经元的个数为embedding vector*field_size。dense_feature是embeding层的输出的水平拼接。

DNN部分的结构

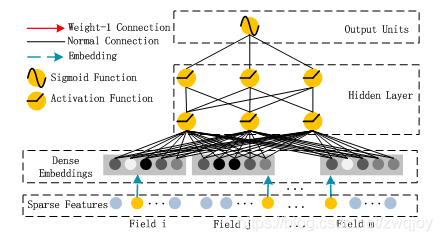
这里DNN的作用是构造高维特征，且有一个特点：DNN的输入也是embedding vector。所谓的权值共享指的就是这里。

关于DNN网络中的输入a处理方式采用前向传播，如下所示：

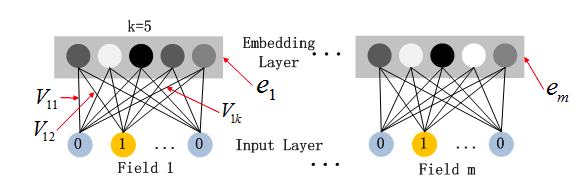
这里假设a(0)=(e1,e2,...em) 表示 embedding层的输出，那么a(0)作为下一层 DNN隐藏层的输入，其前馈过程如下。

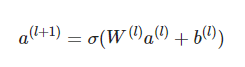
1）不管每个Field的特征是否相同，但embedding后其特征向量维度均为k

2）利用FM中隐向量Vi来作为子网络的初始化权重来获得Field的隐向量。

三.代码相关部分说明

1.对1个feature的稀疏向量进行紧凑化处理

首先是Sparse Vector到 Dense Vector的Embedding层。

前置知识是离散特征的向量化

 
    #假设有特征gender
    values = (male,female,trans)
    #one-hot之后会得到长为3的vector
    #e.g. 
    v = [0,1,0]
     
    #如果取值有1万种，那么len(v)=10^4，而这么长的vector里面只有一个1
    #我们希望把它压缩到一个比较亲近人类的长度，e.g.300
    #于是有
    feature_size = 10^4
    embedding_size= 300
     
    #构建embedding层
    import torch
    import torch.nn as nn
     
    embd_layer = nn.Embedding(feature_size, embedding_size) 

2.从1个feature扩展到n个features

    #现在我们有n个features
    #每个feature的取值分别有feature_size种，存在一个list中。
     
    #伪代码
    features = [age,gender,work]
    feature_sizes = []
    for feature in features:
        feature_size=len(feature)
        feature_sizes.append(feature_size)
        
     
    #于是我们可以求相关参数
    #在FM算法中，作者把一个字段作为一个field，于是我们可以根据传入的参数，知道有多少个field
    n_fields = len(feature_sizes)
     
     
    #再对每一个field都建立embedding
    embedding_size = 300
    embd_layers = nn.ModuleList(
        [nn.Embedding(feature_size, embedding_size) for feature_size in self.feature_sizes]
    )
     
    #我们希望每一种feature，embd之后的size都是相同的，所以这里统一使用了300。

完成之后我们得到了更加紧凑的dense feature，注意这个dense_feature是embedding层的输出的水平拼接。

所以可以算得其 dim = n个field * 每个300维  = 300*n 维 

3.Deep部分 把dense_feature传入神经网络

#把300*n维的维度信息提出来
dense_dim =  n_fields * embedding_size
 
#设定两个全连接层的维度，简便起见假设它们维度相同
fc_dim = 100
 
 
#现在我们要丢dense_feature进去
 
self.fc_layer1 = nn.Sequential(
            nn.Linear(dense_dim,fc_dim),
            nn.BatchNorm2d(fc_dim),
            nn.LeakyReLU(0.2, inplace=True)     
)
 
self.fc_layer2 = nn.Sequential(
            nn.Linear(fc_dim,fc_dim),
            nn.BatchNorm2d(fc_dim), 
            nn.LeakyReLU(0.2, inplace=True)     
)
 

进行的是如下图红色这部分：

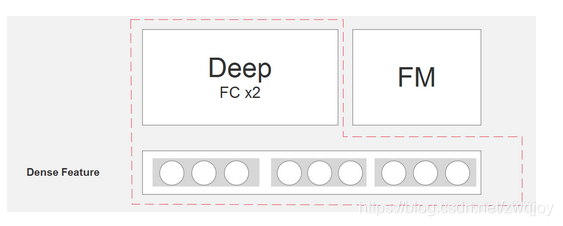
4.FM部分，根据sparse feature计算二阶项的预测值

对每一个field，都有一个(feature_size, embedding_size)的参数矩阵。还是以gender为例，这个矩阵shape=(3,300)

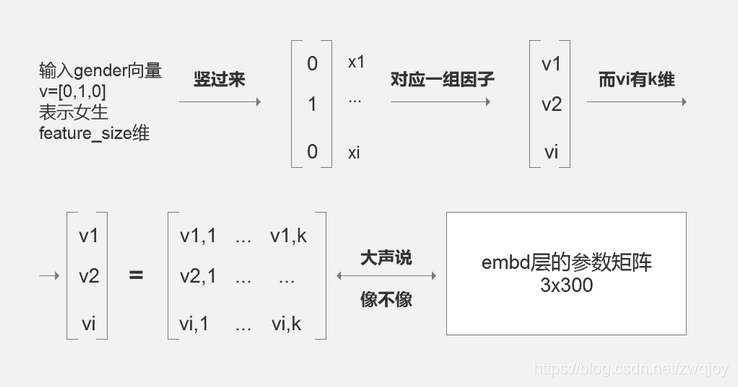
默认你已经自学完成了理论部分。

那么这就是参数共享了，因为形状一样，所以可以用embd层的参数矩阵，去代替FM部分隐因子的参数矩阵。

现在，我们的问题就是，如何用代码来表达推导公式：

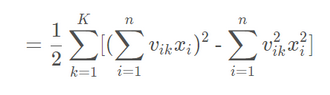
备注：原论文的版本，把小k换成小f，网上流传的也多是遵循原版使用字符f。字母不影响达意。

我们把这个式子分为两部分。

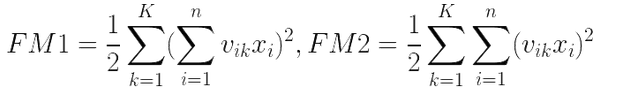
原式 = FM1-FM2

1. FM1计算方法

 容易知道，v'x的每一行都是 k=f 时的

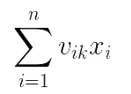
例如v'x的第1行是k=1时的上式。而v'x的shape = (k,1)，是一个k维的列向量，共含有k个元素。

显然我们只需要对v'x的k个元素，逐个平方，再sum，接着乘1/2，即可得到FM1。

2. FM2计算方法

如果你用过matlab之类的东西，应该知道点运算。 ^2表示逐元素取平方。

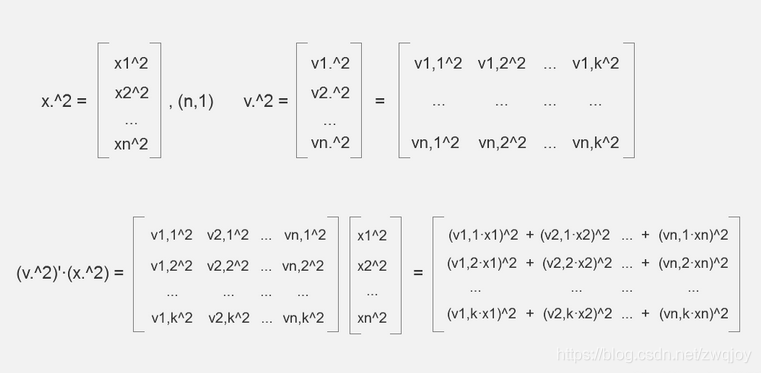
 显然(v^2)'·(x^2) 的每一行的，都是k=f时的

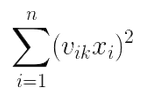
我们只需要对(v^2)'·(x^2) 的每行sum加和，接着乘1/2，即可得到FM2。

这就是FM因子分解机理论上的计算方式

3. 优化计算方法

然而这样做的操作量很大，每个矩阵大小=n*k = feature_size * embedding_size

又考虑到，我们输入的特征向量x是稀疏的！

虽然shape=(n,1)，但是n个元素里面只有1个1，其他(n-1)个都是0

那么，假设我们知道那个1的下标值，例如我们知道xi=1，而其他的 xj = 0 , ( j=1,2,3,...n, j ≠ i )。

我们的整个计算过程，就可以只关注vi ,shape = (1,k)，和 xi , shape = (1,1)

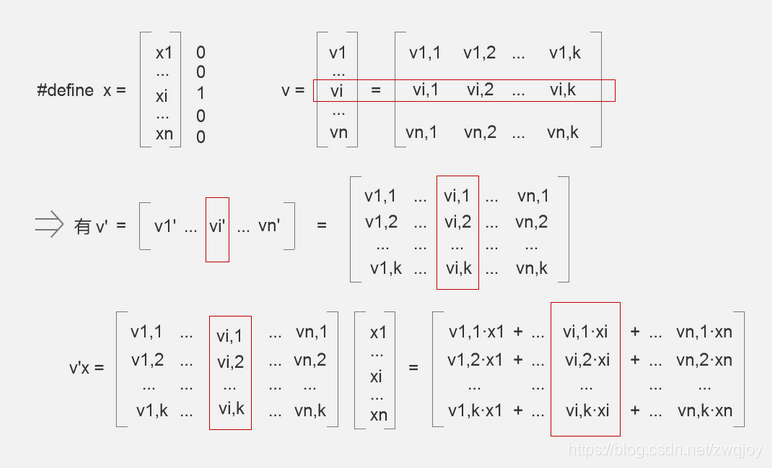
而xi=1，怎么乘都不影响vi的值，所以进一步的，我们只需要关注vi。

这样计算值就极大地缩减了。

（当然，为了让模型具备泛化能力，我们先不假定xi=1，而是假定xi等于某个不为0的数字。）

于是，最终我们需要的结果就转变成了，vi·xi ，xi是一个很可能为1的数字，vi是(1,k)行向量。

这就是为什么在广告CTR等领域你才能看到FM理论的大量应用，因为这些地方的特征都是极为稀疏的。

【特征的特征决定了我们选取的处理特征的理论】

而上文说过，由于我们强行使用参数共享，所以 v=embedding矩阵，shape=(feature_size, embedding_size)。

import torch
import torch.nn as nn
 
# 先建立一个简单的embd层，
embedding_size = 5
feature_size = 3
embd_layer = nn.Embedding(feature_size, embedding_size)
 
# 如果对第n个field，我们知道一个下标i，使得xi为当前field的唯一非0值。
idx = torch.LongTensor([1])
# 在pytorch中，我们可以这样取出vi
vi = embd_layer(idx)  # shape = (1,embedding_size) =(1,k)
'''
>>> vi.shape
torch.Size([1, 5])
>>> vi
tensor([[-1.1124, -0.7023, -0.8200,  1.6422,  0.2136]],
       grad_fn=<EmbeddingBackward>)
>>> 
'''
 
# ----------------
# 如果对第n个field，我们有m个样本的下标构成一个tensor
batch_idx = torch.LongTensor([0, 1, 2])  # shape=(m)
batch_vis = embd_layer(batch_idx)  # shape=(m,k)
'''
>>> batch_vis.shape
torch.Size([3, 5])
>>> batch_vis
tensor([[-0.9178,  1.1880,  0.9566, -0.9948,  0.9113],
        [-1.1124, -0.7023, -0.8200,  1.6422,  0.2136],
        [-0.4018, -0.0844,  0.9122, -1.7312,  1.5130]],
       grad_fn=<EmbeddingBackward>)
'''
 
# 再有m个样本的对应xi的值
batch_xis = torch.FloatTensor([1, 1, 1])  # shape=(m)
 
# 我们让每个样本的vi与对应的xi相乘
res = (batch_vis.t()) * batch_xis  # (k,m)*(m)=(k,m)
res = res.t()  # shape=(m,k)
 
# 由前面的讨论知道，此时res的每行，
# 都是第m个样本在第n个field的(v'x)'=vixi，即长度为k的行向量
# [vi1xi,vi2xi,...,vikxi]

我们解决了一个field内m个sample的问题，现在可以把问题扩展到全部n个field了。

继续，我们要把n个field的vixi全部算出来。

    import torch
    import torch.nn as nn
     
     
    #对n个field搭建model
     
    n_field = 4                 #有4个字段 
    feature_sizes= [5,3,6,4]    #每个字段向量化后的长度分别为5,3,6,4
    embedding_size = 30        #希望以k=30来表达这些向量
     
     
    n_embds = nn.ModuleList(
    [nn.Embedding(feature_sizes[i], embedding_size) for i in range(n_fileds)]
    )
     
     
    #从n_field个字段内提取唯一的非零值对应的vixi
     
    #假设有一个存储idx的文件，m个样本在n个field对应的非零项的下标
    #shape=(m_samples,n_field)
    train_idx = read_from_file('xx.file') 
     
    #再有m个样本在n个field对应的非零项xi的值，shape=(m_samples,n_field)
    train_values = read_from_file('xxxxx.file') 
     
    results = []
    for i , module in enumerate(n_embds):
        #当前为 i_th_field
        batch_idx = torch.Tensor(train_idx[:,i])         #shape=(m)
        batch_vis = module(batch_idx)                    #shape=(m,k)
        batch_xis = torch.FloatTensor(train_values[:,i]) #shape=(m)
     
        #我们让每个样本的vi与对应的xi相乘
        res = (batch_vis.t())*train_values    #(k,m)*(m)=(k,m)
        res = res.t()                         #shape=(m,k)
        results.append(res)
     
    #由前面的讨论知道，此时res的每行，
    #都是第m个样本在第n个field的(v'x)'=vixi，即长度为k的行向量
    #[vi1xi,vi2xi,...,vikxi]

现在我们得到了一个results列表。

需要用它来算FM1和FM2。

观察公式，对FM1，我们需要固定K不动，先sum一轮vikxi，然后逐项平方。最后逐K累加。

对FM2，我们需要固定K不动，先平方vikxi，再sum。最后逐个K累加。

先看FM1，以K为轴，先固定K不动。

(1)以n为维度sum一次。其实就是把results这个 list of tensor里面的每一个shape相同的tensor ，在相同位置上全部加起来。

fm1_step1 = sum(results)    #sum(n*[m,k]) -> (m,k)，此处必须使用python原生sum()

(2)然后逐项平方。

fm1_step2 = fm1_step1*fm1_step1  #(m,k)*(m,k)=(m,k)

(3)最后逐K累加。

fm1 = torch.sum(fm1_step2,dim=1) #sum([m,k] ,dim=1) -> (m)

再看FM2，同样以K为轴，先固定K不动。

(1)先进行逐项平方

fm2_step1= [item*item for item in results] #list of n*(m,k)

(2)再以n为维度sum一次。

fm2_step2 = sum(fm2_step1) #sum(n*[m,k]) -> (m,k)，此处必须使用python原生sum()

(3)最后逐K累加。

fm2 = torch.sum(fm2_step2,dim=1)  #sum([m,k],dim=1) -> (m)

最后两者相减，乘系数即可。

quadratic_term = (fm1-fm2)*0.5

至此，我们得到了最后一个二次项。

但是还少了线性部分。

linear_part = nn.ModuleList(
[  nn.Linear(feature_sizes[i]),1)  for i in range(n_field)]
)

现在FM部分被彻底搞定了，我们看看进度条。

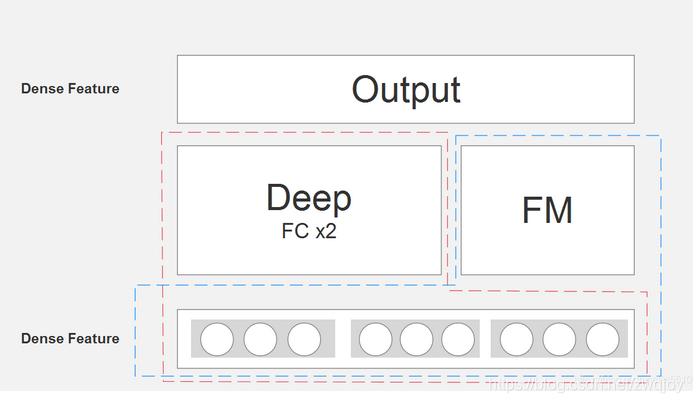
5.合并输出，计算loss

import torch.nn.functional as F
 
 
#设deep部分的输出为 deep_out
total_out = deep_out + quadratic_term  #shape=(m,1)
 
#根据任务不同，这里的输出可以做不同的处理。比如点击率预测就是分类问题了。
#但是我当前的需求是数值预测，所以直接拿来用
 
#随便选一个损失函数，或者自定义
loss_func = F.binary_cross_entropy_with_logits
 
#优化器
optimizer = torch.optim.SGD(self.parameters(), lr=self.learning_rate, weight_decay=self.weight_decay)
#optimizer = torch.optim.Adam(self.parameters(), lr=self.learning_rate, weight_decay=self.weight_decay)
#optimizer = torch.optim.RMSprop(self.parameters(), lr=self.learning_rate, weight_decay=self.weight_decay)
#optimizer = torch.optim.Adagrad(self.parameters(), lr=self.learning_rate, weight_decay=self.weight_decay)
 
 
optimizer.zero_grad()
loss = loss_func(total_out,train_y)
loss.backward()
optimizer.step()

四 DeepFM中Field和特征的理解

论文中的特征就是one-hot编码之后的特征，而Field就相当于一个列，举个例子，比如在FM所展现的例子所示：

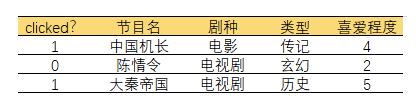
“中国机长”，“陈情令”，“大秦帝国”就是三个特征，但他们属于同一个Field，就是“节目名”。
正如论文中所说，Field可以分为分类和连续两种类型，分类类型要经过one-hot编码，而连续类型就是自己本身的数值value。这样，每个样本都可以表示为

其中如果field<j>是category类型的，那么通过one-hot编码，就是个高维稀疏的矩阵，每一列都是一个特征；若是连续类型的Field就是它的特征，其value为原来的特征值，如上图中的“喜爱程度”。

首先要明确数据的格式应该是怎样的。

我们假设现在要解决的问题是一个CTR预估问题，数据集是 (X,y)，每一个样本都是高度稀疏的高维向量。假设我们有两种 field 的特征，连续型和离散型，连续型 field 一般不做处理沿用原值，离散型一般会做One-hot编码。离散型又能进一步分为单值型和多值型，单值型在Onehot后的稀疏向量中，只有一个特征为1，其余都是0，而多值型在Onehot后，有多于1个特征为1，其余是0。

下面给出一个两个样本的例子，其中shop_score是连续型field，gender是单值离散型field，interest是多值离散型field。可以看到shop_score的取值是实数，gender的取值是离散值，interest的取值是离散值序列。

对各field进行Onehot后，可见单值离散field对应的独热向量只有一位取1，而多值离散field对应的独热向量有多于一位取1，表示该field可以同时取多个特征值。

进一步，我们对每个field中的特征取值分别单独编码或联合编码，则确定了特征的index，这在libsvm数据格式中是需要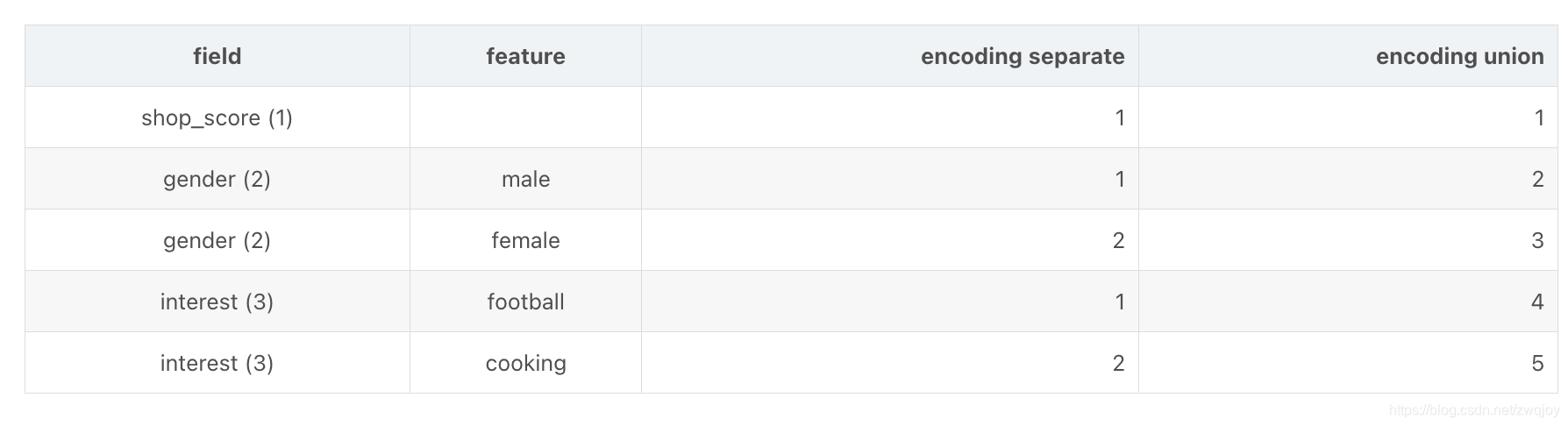

libsvm格式：

可见，连续field和单值field对样本长度的贡献恒定为1，但多值离散型field可能会导致样本长度不一样。对不定长样本的处理方法自然是padding补零了

可以选择对每个多值field分别进行padding，原因有二。

首先，若对样本整体进行padding，万一想要进行截断，可能会截掉某些连续field和单值field，分别padding则可以分别截断，而不影响其他的field。

第二，对每个field的不同特征单独编码互不影响，不需要维护一个全局的字典，每次只需要处理一个field的特征，甚至可以实现并行处理以及节省内存的特征Encoding方案。

FM所需的数据格式正是libsvm格式，既需要数值本身（Value），也需要特征取值在字典中的index（ID）。

假如我们采用对每个field的不同特征取值单独编码的方式，则可以实现一些简便性优化。首先，数值型field的ID永远是1，因此可以省略ID；第二，单值离散型field的Value永远是1，因此可以省略Value；第三，多值离散型field可以用padding+masking的方式省略ID。

 

用Embedding实现 FM一次项 ∑wixi

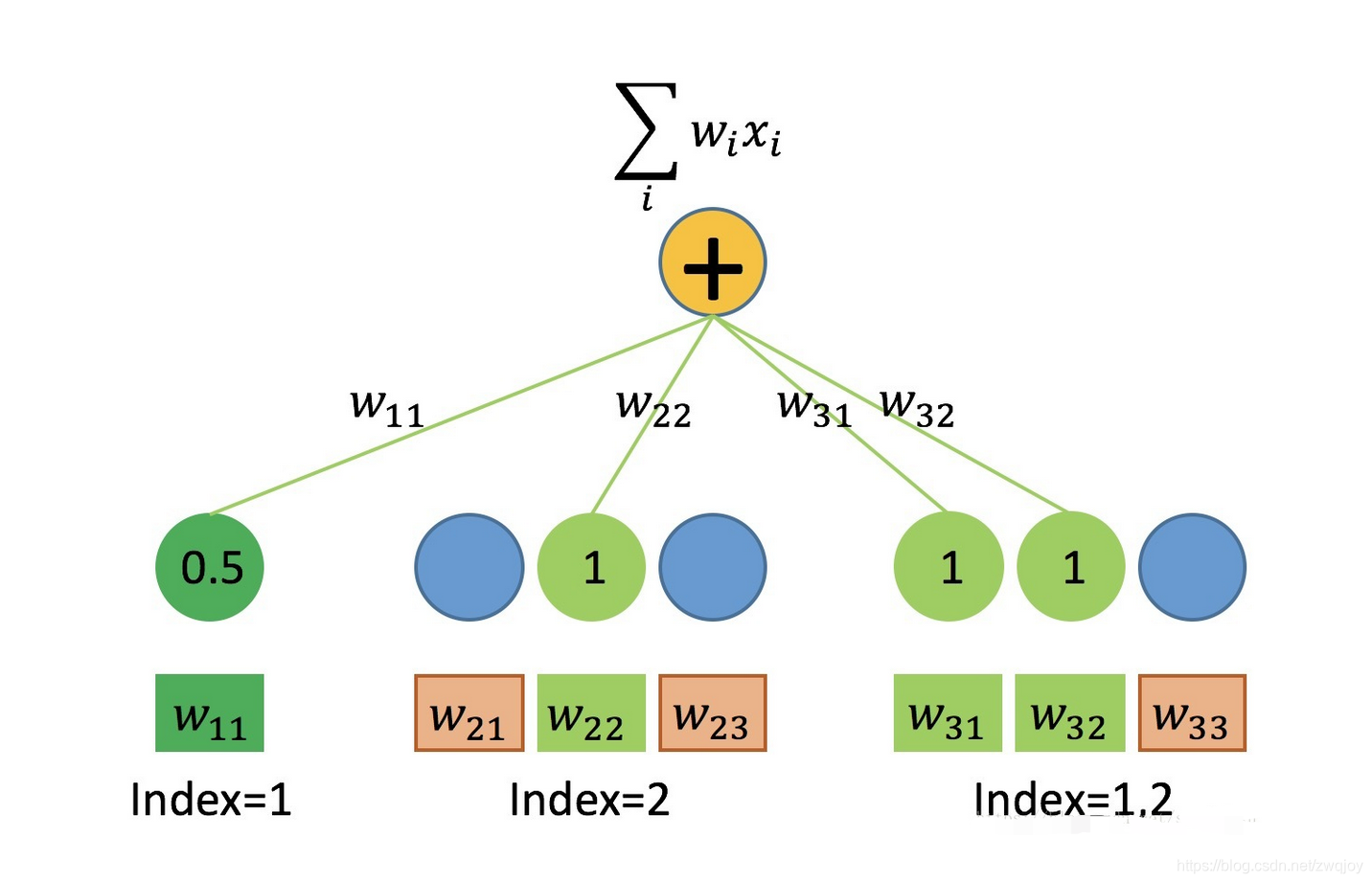
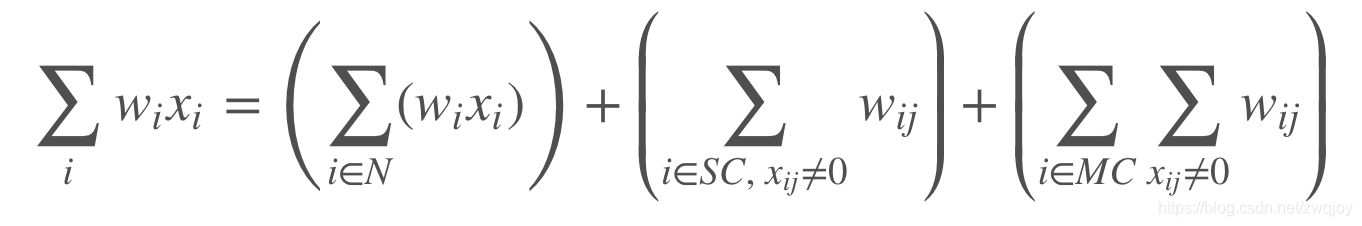
如上所述，我们的输入数据有三种field，在One-hot处理后代入FM一次项的公式运算。每个field各有一个权值向量w，连续型field的w长度为1，离散型field的w长度为特征的取值个数。
  首先，连续型field对一次项的贡献等于自身数值乘以权值w，可以用Dense(1)层实现，任意个连续型field输入到同一个Dense层即可，因此在数据处理时，可以先将所有连续型field拼成一个大矩阵，同时如上所述，ID可以省略。
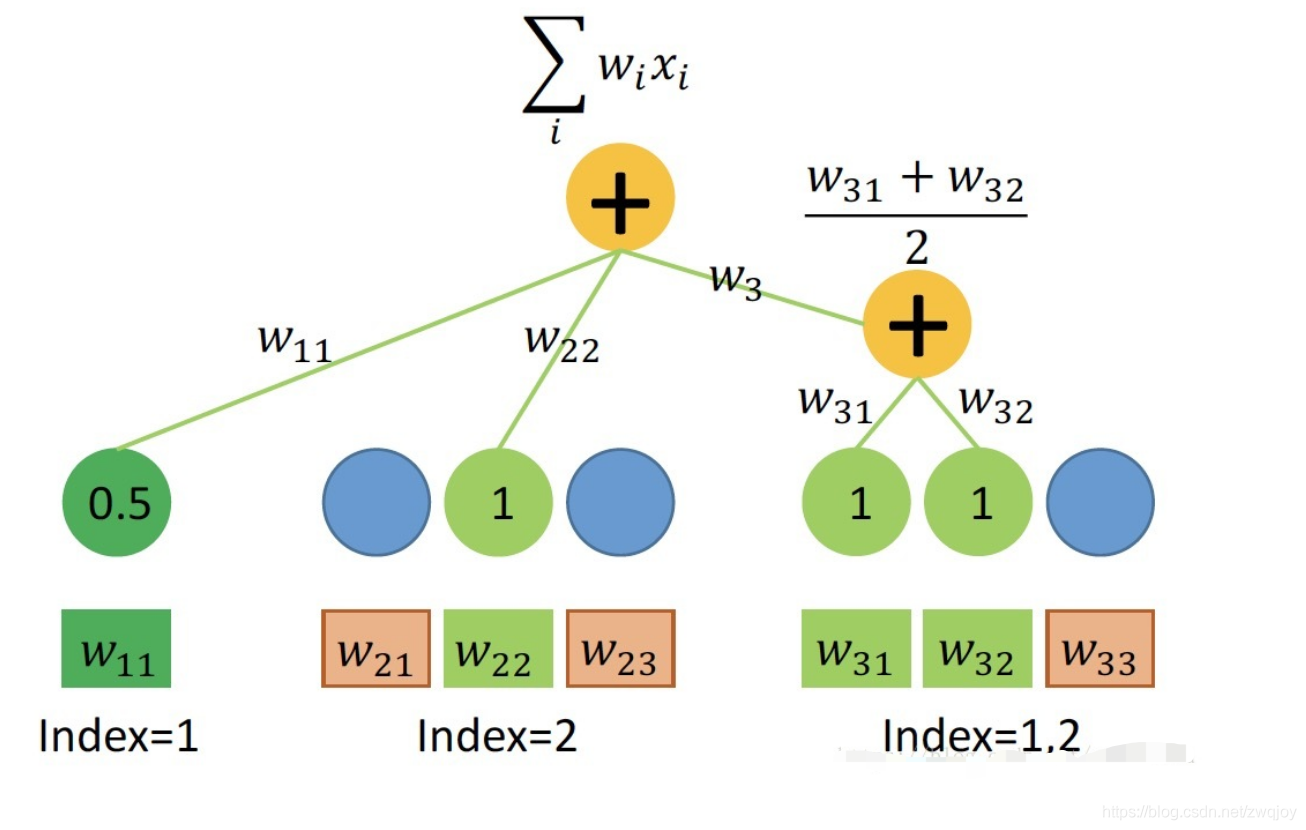
  其次，单值离散型field根据样本特征取值的index，从w中取出对应权值（标量），由于离散型特征值为1，故它对一次项的贡献即取出的权值本身。取出权值的过程称为 table-lookup，可以用Embedding(n,1)层实现（n为该field特征取值个数）。若将所有单值离散型field的特征值联合编码，则可使用同一个Embedding Table进行lookup，不需要对每个field单独声明Embedding层。因此在数据处理时，可以先将所有单值离散型field拼起来并联合编码，同时如上所述，Value可以省略，只关心lookup出来的权值w

即可。
  最后，多值离散型field可以同时取多个特征值，为了batch training，必须对样本进行补零padding。相似地可用Embedding层实现，Value并不是必要的，但Value可以作为mask来使用，当然也可以在Embedding中设置mask_zero=True。
  如下图所示，假设我们有m个连续型field，n个单值离散型field，q个多值离散型field，每个多值离散型field的最长长度为Li(i=1,2,⋯,q)

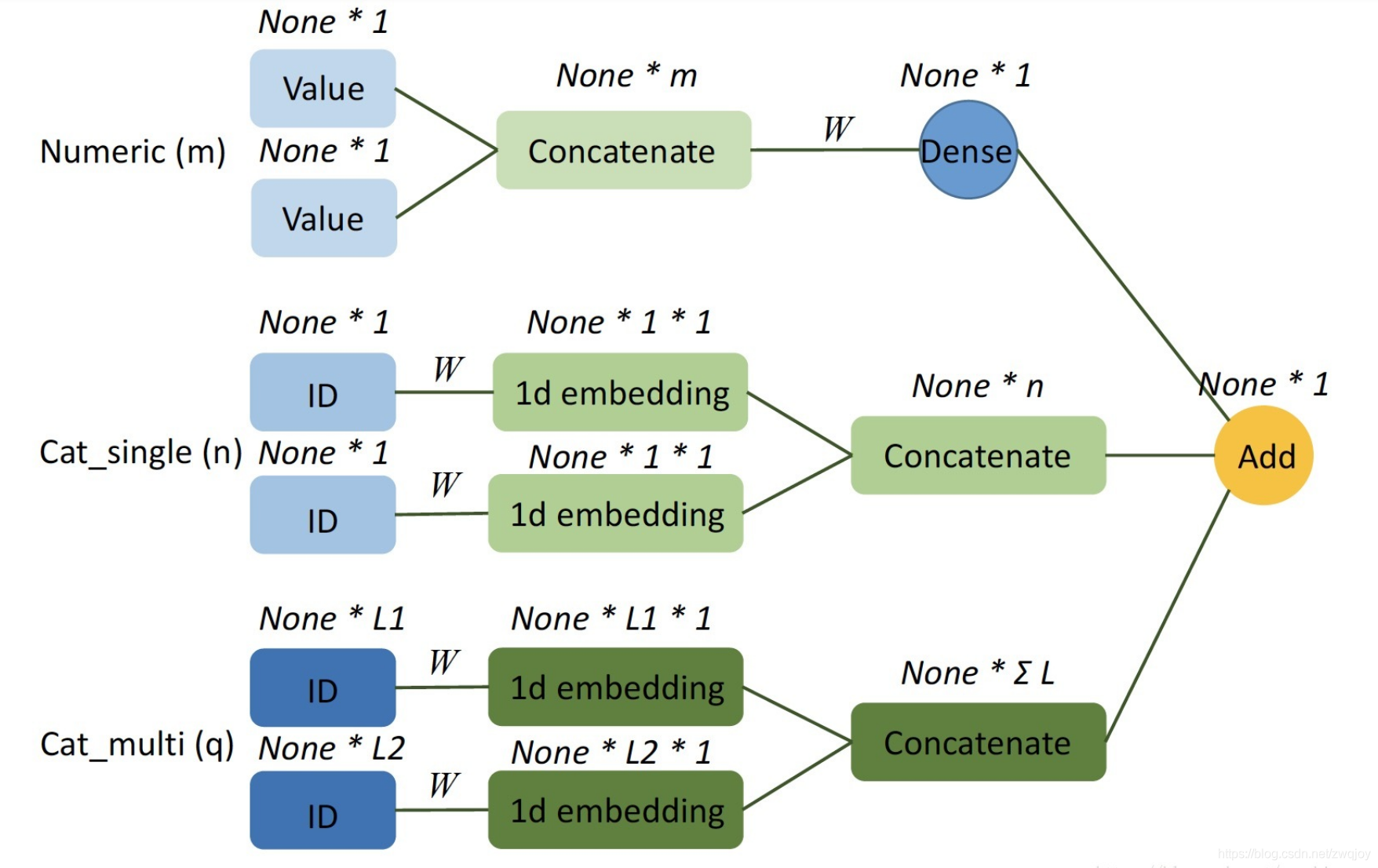
用Embedding实现FM二次项 ∑∑(vi⋅vj)⋅xixj

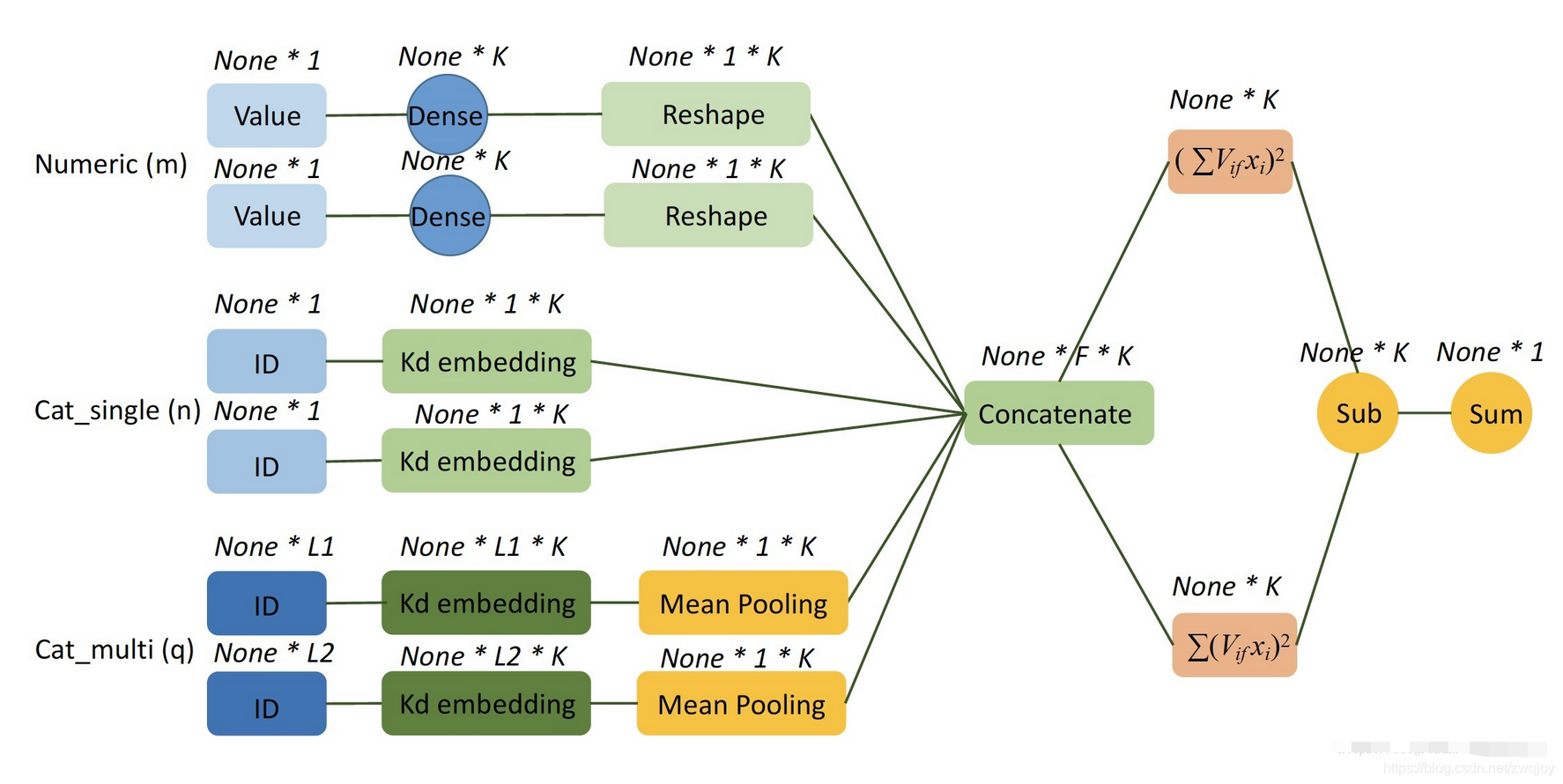
 由于FM的二次项是不同特征之间的交叉（一般是不同field之间的交叉），不能分field实现，必须将每个field输入Embedding后拼接起来，再求二次项。

实现一个DNN

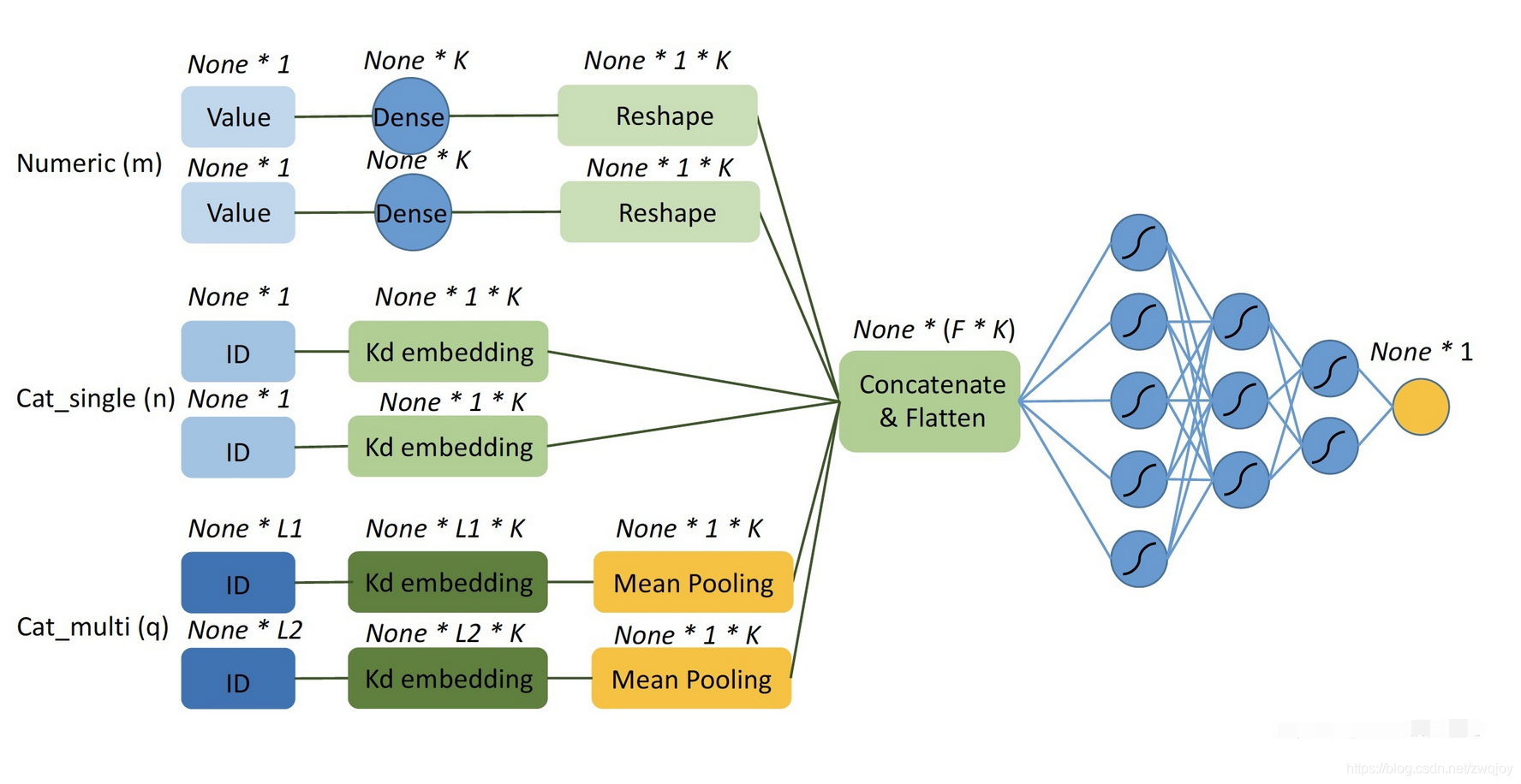
DNN从FM二次项倒数第二步生成的 None*F*K Embedding 张量开始，先用Flatten层平铺，然后经过若干层神经网络，每一层后面可以加上dropout防止过拟合和BatchNormalization加速收敛。

Keras例子：

import numpy as np
from keras.layers import *
from keras.models import Model
from keras import backend as K
from keras import optimizers
from keras.engine.topology import Layer
 
# 样本和标签，这里需要对应自己的样本做处理
train_x = [
    np.array([0.5, 0.7, 0.9]),
    np.array([2, 4, 6]),
    np.array([[0, 1, 0, 0, 0, 1, 0, 1], [0, 1, 0, 0, 0, 1, 0, 1],
              [0, 1, 0, 0, 0, 1, 0, 1]])
]
 
label = np.array([0, 1, 0])
# 输入定义
continuous = Input(shape=(1,), name='single_continuous')
single_discrete = Input(shape=(1,), name='single_discrete')
multi_discrete = Input(shape=(8,), name='multi_discrete')
 
# FM 一次项部分
continuous_dense = Dense(1)(continuous)
single_embedding = Reshape([1])(Embedding(10, 1)(single_discrete))
multi_dense = Dense(1)(multi_discrete)
# 一次项求和
first_order_sum = Add()([continuous_dense, single_embedding, multi_dense])
 
# FM 二次项部分 k=3
continuous_k = Dense(3)(continuous)
single_k = Reshape([3])(Embedding(10, 3)(single_discrete))
multi_k = Dense(3)(multi_discrete)
 
# 先相加后平方
sum_square_layer = Lambda(lambda x: x ** 2)(
    Add()([continuous_k, single_k, multi_k]))
# 先平方后相加
continuous_square = Lambda(lambda x: x ** 2)(continuous_k)
single_square = Lambda(lambda x: x ** 2)(single_k)
multi_square = Lambda(lambda x: x ** 2)(multi_k)
square_sum_layer = Add()([continuous_square, single_square, multi_square])
 
substract_layer = Lambda(lambda x: x * 0.5)(
    Subtract()([sum_square_layer, square_sum_layer]))
 
 
# 定义求和层
class SumLayer(Layer):
    def __init__(self, **kwargs):
        super(SumLayer, self).__init__(**kwargs)
 
    def call(self, inputs):
        inputs = K.expand_dims(inputs)
        return K.sum(inputs, axis=1)
 
    def compute_output_shape(self, input_shape):
        return tuple([input_shape[0], 1])
 
 
# 二次项求和
second_order_sum = SumLayer()(substract_layer)
# FM 部分输出
fm_output = Add()([first_order_sum, second_order_sum])
# deep 部分
deep_input = Concatenate()([continuous_k, single_k, multi_k])
deep_layer_0 = Dropout(0.5)(Dense(64, activation='relu')(deep_input))
deep_layer_1 = Dropout(0.5)(Dense(64, activation='relu')(deep_layer_0))
deep_layer_2 = Dropout(0.5)(Dense(64, activation='relu')(deep_layer_1))
deep_output = Dropout(0.5)(Dense(1, activation='relu')(deep_layer_2))
concat_layer = Concatenate()([fm_output, deep_output])
y = Dense(1, activation='sigmoid')(concat_layer)
model = Model(inputs=[continuous, single_discrete, multi_discrete], outputs=y)
Opt = optimizers.Adam(
    lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False)
model.compile(
    loss='binary_crossentropy',
    optimizer=Opt,
    metrics=['acc'])
model.fit(
    train_x,
    label,
    shuffle=True,
    epochs=1,
    verbose=1,
    batch_size=1024,
    validation_split=None)

参考资料

• 论文
• FFM及DeepFFM模型在推荐系统的探索
• 深度推荐模型之DeepFM

• DeepFM算法解析及Python实现

• deepFM in pytorch

• 用Keras实现一个DeepFM