NNDL 作业11：优化算法比较_优化算法在mnist数据集上收敛性的比较

文章目录

前言

一、1. 编程实现图6-1，并观察特征

二、观察梯度方向

三、3. 编写代码实现算法，并可视化轨迹

四、4. 分析上图，说明原理（选做）

1、为什么SGD会走“之字形”？其它算法为什么会比较平滑？

2、Momentum、AdaGrad对SGD的改进体现在哪里？速度？方向？在图上有哪些体现？

Momentum

 Adagrad

3、仅从轨迹来看，Adam似乎不如AdaGrad效果好，是这样么？

​4、四种方法分别用了多长时间？是否符合预期？

5、调整学习率、动量等超参数，轨迹有哪些变化？

​

五、5. 总结SGD、Momentum、AdaGrad、Adam的优缺点（选做）

六、6. Adam这么好，SGD是不是就用不到了？（选做）

七、7. 增加RMSprop、Nesterov算法。（选做）

八、基于MNIST数据集的更新方法的比较（选做） 

 总结

---

前言

          首先，这次写的很细，而且通过对画图的对比，真的理解上课老师说的一些公式，在看了老师写的代码之后的，会真的明白了好多。

          由于疫情好点了，可是我感觉莲池还是好严重，但是由于放开了，所以我们又搬了(哈哈哈)。

           最后，写的不太好，请老师和各位大佬多教教我(哈哈哈)。

---

一、1. 编程实现图6-1，并观察特征

# coding=gbk
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
 
 
# https://blog.csdn.net/weixin_39228381/article/details/108511882
 
def func(x, y):
    return x * x / 20 + y * y
 
 
def paint_loss_func():
    x = np.linspace(-50, 50, 100)  # x的绘制范围是-50到50，从改区间均匀取100个数
    y = np.linspace(-50, 50, 100)  # y的绘制范围是-50到50，从改区间均匀取100个数
 
    X, Y = np.meshgrid(x, y)
    Z = func(X, Y)
 
    fig = plt.figure()  # figsize=(10, 10))
    ax = Axes3D(fig)
    plt.xlabel('x')
    plt.ylabel('y')
 
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
    plt.show()
 
 
paint_loss_func()

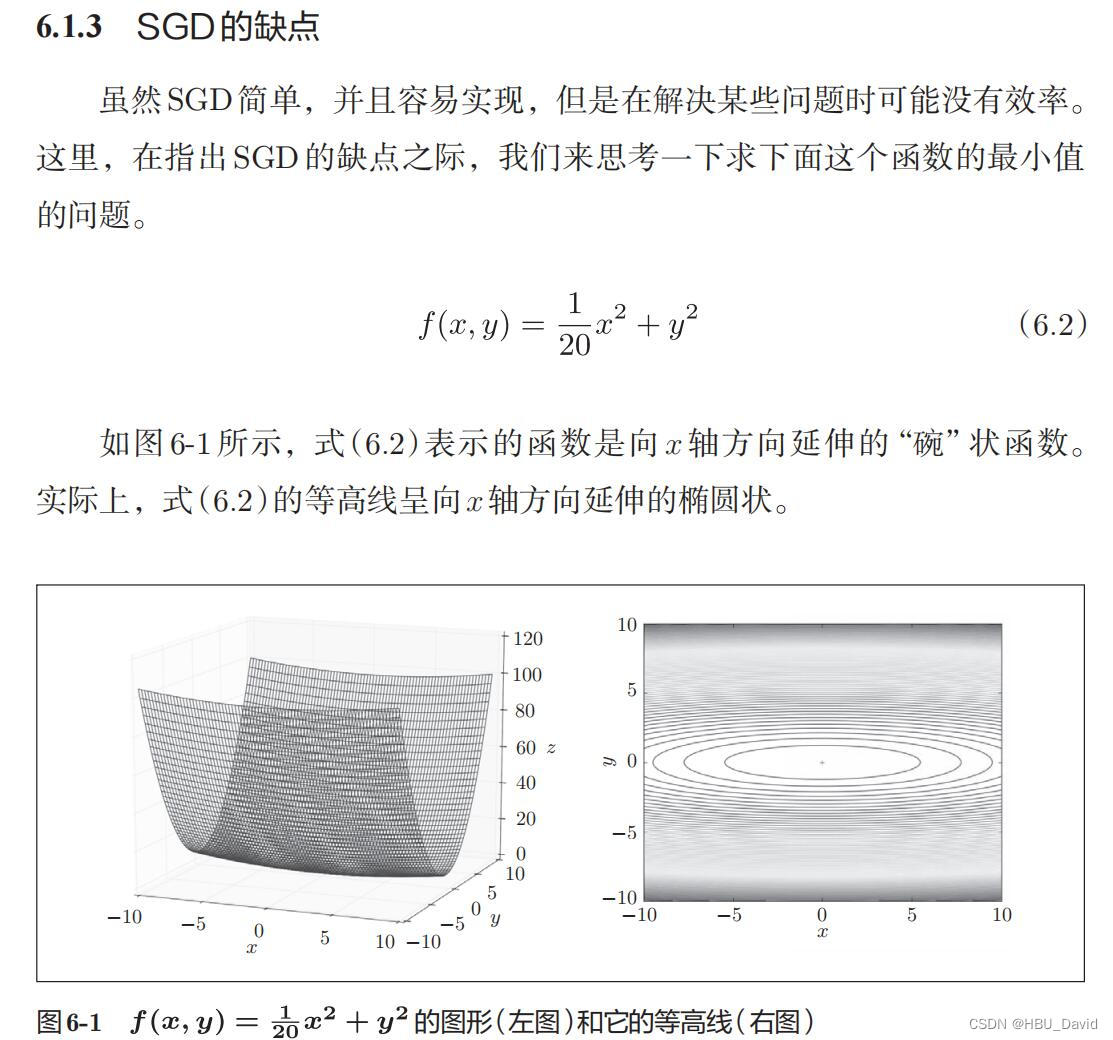
运行结果为：

       说一下特点，注意上课老师说了，最后那是底边个弧线，所以是有最低点的，大家一定要注意。  

二、观察梯度方向

 

就像我说的，底边是条弧线，所以最低点只有中间那个点，y轴方向大，x轴方向小，好多地方没有指向(0,0)。 

 三、3. 编写代码实现算法，并可视化轨迹

SGD、Momentum、Adagrad、Adam

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
 
 
class SGD:
    """随机梯度下降法（Stochastic Gradient Descent）"""
 
    def __init__(self, lr=0.01):
        self.lr = lr
 
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]
 
 
class Momentum:
    """Momentum SGD"""
 
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
 
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]
 
 
class Nesterov:
    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""
 
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
 
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]
 
 
class AdaGrad:
    """AdaGrad"""
 
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
 
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
 
 
class RMSprop:
    """RMSprop"""
 
    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None
 
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
 
 
class Adam:
    """Adam (http://arxiv.org/abs/1412.6980v8)"""
 
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
 
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
 
        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
 
        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
 
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
 
 
def f(x, y):
    return x ** 2 / 20.0 + y ** 2
 
 
def df(x, y):
    return x / 10.0, 2.0 * y
 
 
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
 
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
 
idx = 1
 
for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
 
    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])
 
        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)
 
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
 
    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)
    # for simple contour line
    mask = Z > 7
    Z[mask] = 0
 
    # plot
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)  # 绘制等高线
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")
 
plt.subplots_adjust(wspace=0, hspace=0)  # 调整子图间距
plt.show()

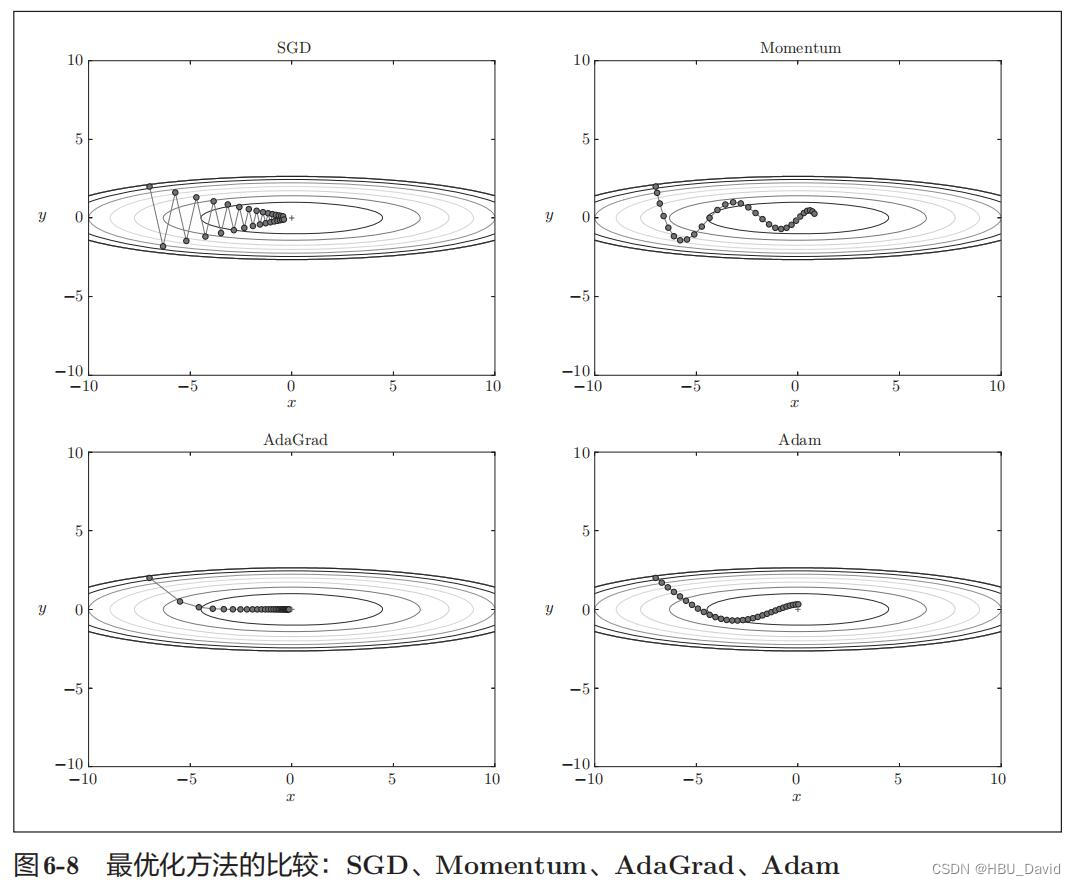
运行结果为：

 

四、4. 分析上图，说明原理（选做）

1、为什么SGD会走“之字形”？其它算法为什么会比较平滑？

        SGD有缺陷，呈现之字形，是因为图像的变化并不均匀，所以y方向变化很大时，x方向变化很小，只能迂回往复地寻找，效率很低。

       SGD 呈“之”字形移动。这是一个相当低效的路径。也就是说，SGD 的缺点是，如果函数的形状非均向（anisotropic），比如呈延伸状，搜索的路径就会非常低效。因此，我们需要比单纯朝梯度方向前进的 SGD 更聪明的方法。

        SGD 低效的根本原因是，梯度的方向并没有指向最小值的方向。为了改正SGD的缺点，引入了Momentum、AdaGrad、Adam这 3 种方法来取代SGD。

2、Momentum、AdaGrad对SGD的改进体现在哪里？速度？方向？在图上有哪些体现？

Momentum

        为了抑制SGD的震荡，SGDM认为梯度下降过程可以加入惯性。下坡的时候，如果发现是陡坡，那就利用惯性跑的快一些。SGDM全称是SGD with momentum，在SGD基础上引入了一阶动量：一阶动量是各个时刻梯度方向的指数移动平均值，约等于最近 1/(1-β1) 个时刻的梯度向量和的平均值。

       也就是说，t 时刻的下降方向，不仅由当前点的梯度方向决定，而且由此前累积的下降方向决定。β1的经验值为0.9，这就意味着下降方向主要是此前累积的下降方向，并略微偏向当前时刻的下降方向。想象高速公路上汽车转弯，在高速向前的同时略微偏向，急转弯可是要出事的。

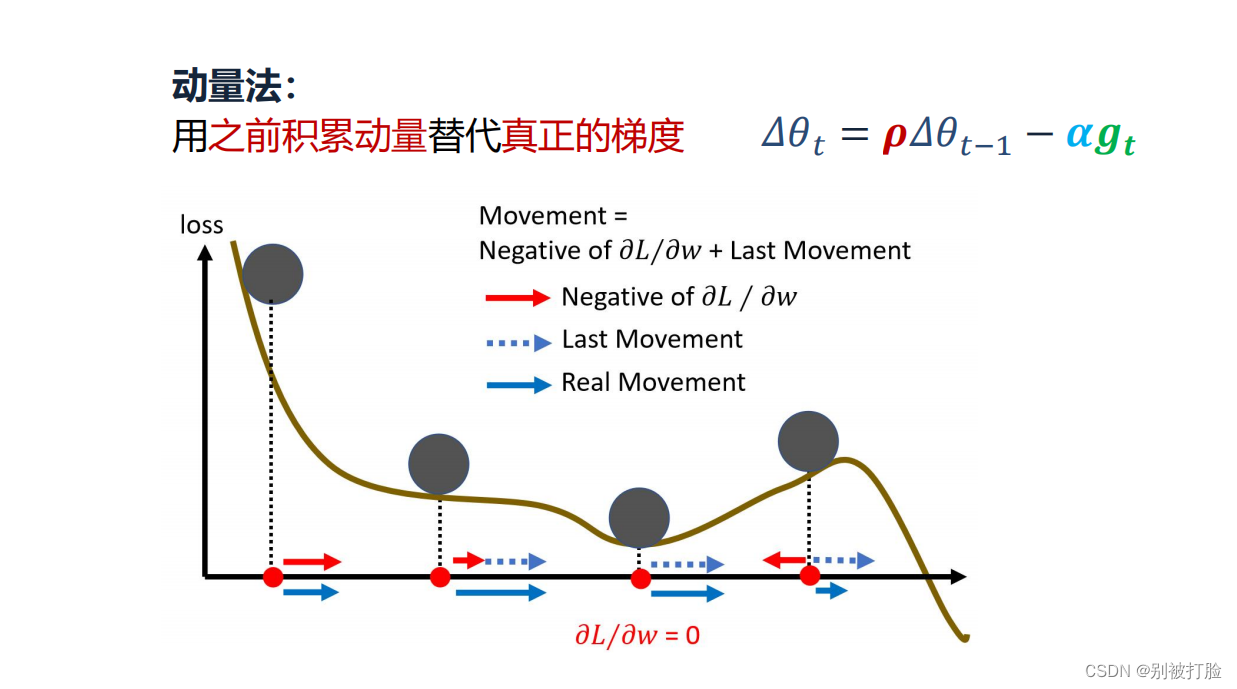
       动量优化法，相比于SGD仅仅关注当前的梯度，该方法引入了动量向量的概念，参数沿着动量向量进行更新，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。公式表示如下图所示，dW与db分别表示当前的权重梯度和偏移量梯度，其中β取值越大，过去的梯度影响越大，梯度下降更加顺滑，但是β太大也不行，一般取到0.9。

 总的来说，该方法从梯方面进行了优化。

 Adagrad

      怎么样去度量历史更新频率呢？那就是二阶动量——该维度上，迄今为止所有梯度值的平方和：

      我们再回顾一下步骤3中的下降梯度：

       可以看出，此时实质上的学习率由变成了。 一般为了避免分母为0，会在分母上加一个小的平滑项。因此是恒大于0的，而且参数更新越频繁，二阶动量越大，学习率就越小。

       这一方法在稀疏数据场景下表现非常好。但也存在一些问题：因为是单调递增的，会使得学习率单调递减至0，可能会使得训练过程提前结束，即便后续还有数据也无法学到必要的知识。

       该方法使梯度在各个维度上按比例地缩小,也就是降低学习率，随着迭代次数的增加，学习率会越来越小，并且在某个维度上越陡峭，学习率降低得就越快，在这个维度上越平缓，学习率降低得就越慢。所以，该方法非常适合处理稀疏数据。公式表示如下图所示，学习率η除以了过往梯度的平方和的开方。

随着训练迭代轮数的增加，学习率会越来越小，后期可能学不到任何东西，导致训练提前结束。
总的来说，该方法是从学习率的角度进行了优化。

3、仅从轨迹来看，Adam似乎不如AdaGrad效果好，是这样么？

       并不是这样的，首先Adam是前述方法的集大成者。我们看到，SGD-M在SGD基础上增加了一阶动量，AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来，就是Adam了——Adaptive + Momentum。

        图像好是以为采纳数的原因，从下边的图就可看出

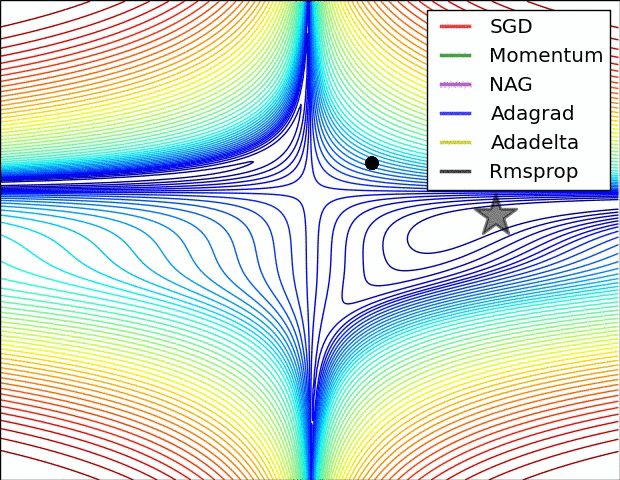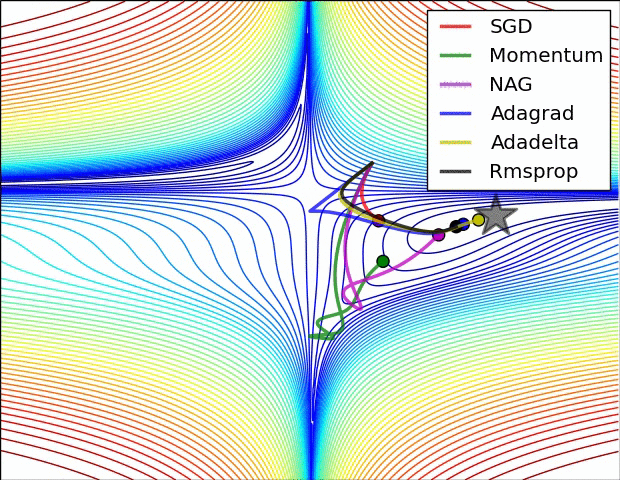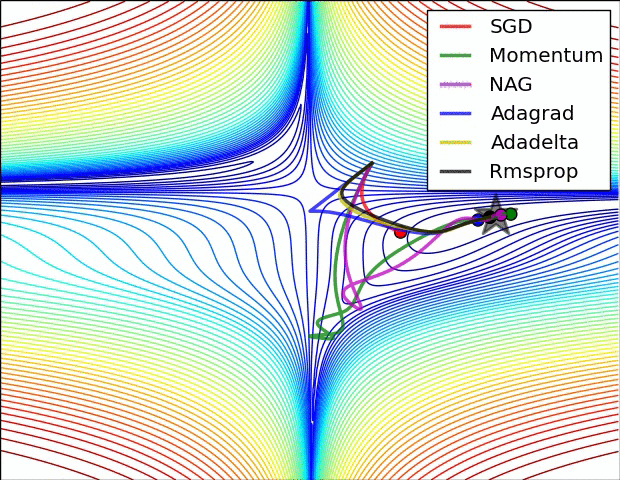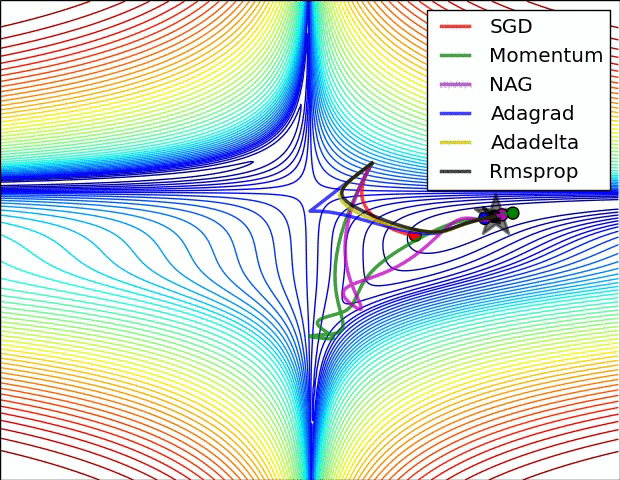
4、四种方法分别用了多长时间？是否符合预期？

0.04188799858093262
0.040869951248168945
0.04188966751098633
0.040892839431762695 

       上边试运行的时间。当然单位是s

       符合预期，由于参数的原因，这个算法的路径几乎都是最优的，所以时间上差不多，但是好一点的算法肯定会快一点。

5、调整学习率、动量等超参数，轨迹有哪些变化？

optimizers["SGD"] = SGD(lr=0.01)
optimizers["Momentum"] = Momentum(lr=0.01)
optimizers["AdaGrad"] = AdaGrad(lr=0.01)
optimizers["Adam"] = Adam(lr=0.01)

运行结果为： 

optimizers["SGD"] = SGD(lr=11)
optimizers["Momentum"] = Momentum(lr=11)
optimizers["AdaGrad"] = AdaGrad(lr=11)
optimizers["Adam"] = Adam(lr=11)

运行结果为： 

optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)

运行结果为： 

        综上来看，最好的肯定是老师的给出的，但是较小的学习率可以看出Adam所需要的计算量会大一点，但是这个看目前来说应该还是主流。 

五、5. 总结SGD、Momentum、AdaGrad、Adam的优缺点（选做）

优化算法
深度学习优化学习方法（一阶、二阶）
一阶方法：随机梯度下降（SGD）、动量（Momentum）、牛顿动量法（Nesterov动量）、AdaGrad（自适应梯度）、RMSProp（均方差传播）、Adam、Nadam。
二阶方法：牛顿法、拟牛顿法、共轭梯度法（CG）、BFGS、L-BFGS。
自适应优化算法有哪些？（Adagrad（累积梯度平方）、RMSProp（累积梯度平方的滑动平均）、Adam（带动量的RMSProp，即同时使用梯度的一、二阶矩））。
梯度下降陷入局部最优有什么解决办法？可以用BGD、SGD、MBGD、momentum，RMSprop，Adam等方法来避免陷入局部最优。

随机梯度下降（SGD）
随机梯度下降法求梯度时选取一个样本j来求梯度。
θj:=wj+α(yi−θiTxi)xj
写成伪代码如下：
for i in range(nb_epochs): np.random.shuffle(data) for example in data: params_grad = evaluate_gradient(loss_function , example ,params) params = params - learning_rate * params_grad
优点：（1）由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。
缺点：（1）准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。（2）可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。（3）不易于并行实现。SGD 因为更新比较频繁，会造成 cost function 有严重的震荡。

①动量梯度下降法（Momentum）
Momentum 通过加入 γ*vt−1 ，可以加速 SGD， 并且抑制震荡。momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力。动量法做的很简单，相信之前的梯度。如果梯度方向不变，就越发更新的快，反之减弱当前梯度。r一般为0.9。
vt=γvt−1+η∇θJ(θ)θ=θ−vt
缺点：这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚，如果它能具备一些先知，例如快要上坡时，就知道需要减速了的话，适应性会更好。

③Adagrad
这个算法就可以对低频的参数做较大的更新，对高频的做较小的更新，也因此，对于稀疏的数据它的表现很好，很好地提高了 SGD 的鲁棒性，例如识别 Youtube 视频里面的猫，训练 GloVe word embeddings，因为它们都是需要在低频的特征上有更大的更新。
梯度更新规则:
θt+1,i=θt,i−ηGt,ii+ϵ⋅gt,i
其中g为t时刻参数θ_i的梯度
gt,i=∇θJ(θi)
如果是普通的 SGD， 那么 θ_i 在每一时刻的梯度更新公式为：
θt+1,i=θt,i−η⋅gt,i
但这里的learning rate η也随t和i而变：
θt+1,i=θt,i−ηGt,ii+ϵ⋅gt,i
其中 Gt 是个对角矩阵， (i,i) 元素就是 t 时刻参数 θi 的梯度平方和。
Adagrad 的优点是减少了学习率的手动调节。超参数设定值：一般η选取0.01。
缺点：它的缺点是分母会不断积累，这样学习率就会收缩并最终会变得非常小。

⑥Adam：Adaptive Moment Estimation
Adam 算法和传统的随机梯度下降不同。随机梯度下降保持单一的学习率（即 alpha）更新所有的权重，学习率在训练过程中并不会改变。而 Adam 通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。这个算法是另一种计算每个参数的自适应学习率的方法，相当于 RMSprop + Momentum。
除了像 Adadelta 和 RMSprop 一样存储了过去梯度的平方 vt 的指数衰减平均值 ，也像 momentum 一样保持了过去梯度 mt 的指数衰减平均值：
mt=β1mt−1+(1−β1)gtvt=β2vt−1+(1−β2)gt2
如果mt和vt被初始化为0向量，那它们就会向0偏置，所以做了偏差校正，通过计算偏差校正后的mt和vt来抵消这些偏差：
m^t=mt1−β1tv^t=vt1−β2t
梯度更新规则:
θt+1=θt−ηv^t+ϵm^t
超参数设定值:建议 β1 ＝ 0.9，β2 ＝ 0.999，ϵ ＝ 10e−8。
实践表明，Adam 比其他适应性学习方法效果要好。
Adam和 SGD区别：Adam = Adaptive + Momentum，顾名思义Adam集成了SGD的一阶动量和RMSProp的二阶动量。

六、6. Adam这么好，SGD是不是就用不到了？（选做）

说到优化算法，入门级必从 SGD 学起，老司机则会告诉你更好的还有 AdaGrad / AdaDelta，或者直接无脑用 Adam。可是看看学术界的最新 paper，却发现一众大神还在用着入门级的 SGD，最多加个 Momentum 或者 Nesterov，还经常会黑一下Adam。比如 UC Berkeley 的一篇论文就在 Conclusion 中写道：

Despite the fact that our experimental evidence demonstrates that adaptive methods are not advantageous for machine learning, the Adam algorithm remains incredibly popular. We are not sure exactly as to why ……

       第一篇就是前文提到的吐槽Adam最狠的UC Berkeley的文章《The Marginal Value of Adaptive Gradient Methods in Machine Learning》。文中说到，同样的一个优化问题，不同的优化算法可能会找到不同的答案，但自适应学习率的算法往往找到非常差的答案（very poor solution）。他们设计了一个特定的数据例子，自适应学习率算法可能会对前期出现的特征过拟合，后期才出现的特征很难纠正前期的拟合效果。但这个文章给的例子很极端，在实际情况中未必会出现。

       另外一篇是《Improving Generalization Performance by Switching from Adam to SGD》，进行了实验验证。他们CIFAR-10数据集上进行测试，Adam的收敛速度比SGD要快，但最终收敛的结果并没有SGD好。他们进一步实验发现，主要是后期Adam的学习率太低，影响了有效的收敛。他们试着对Adam的学习率的下界进行控制，发现效果好了很多。

       于是他们提出了一个用来改进Adam的方法：前期用Adam，享受Adam快速收敛的优势；后期切换到SGD，慢慢寻找最优解。这一方法以前也被研究者们用到，不过主要是根据经验来选择切换的时机和切换后的学习率。这篇文章把这一切换过程傻瓜化，给出了切换SGD的时机选择方法，以及学习率的计算方法，效果看起来也不错。

       这些例子一般过于极端，实际情况中可能未必会这样，但这提醒了我们，理解数据对于设计算法的必要性。优化算法的演变历史，都是基于对数据的某种假设而进行的优化，那么某种算法是否有效，就要看你的数据是否符合该算法的胃口了。

七、7. 增加RMSprop、Nesterov算法。（选做）

对比Momentum与Nesterov、AdaGrad与RMSprop。

这个我直接调的库，我就不直接发了，大家，调库直接画即可。

八、基于MNIST数据集的更新方法的比较（选做） 

在原图基础上，增加RMSprop、Nesterov算法。

编程实现，并谈谈自己的看法。

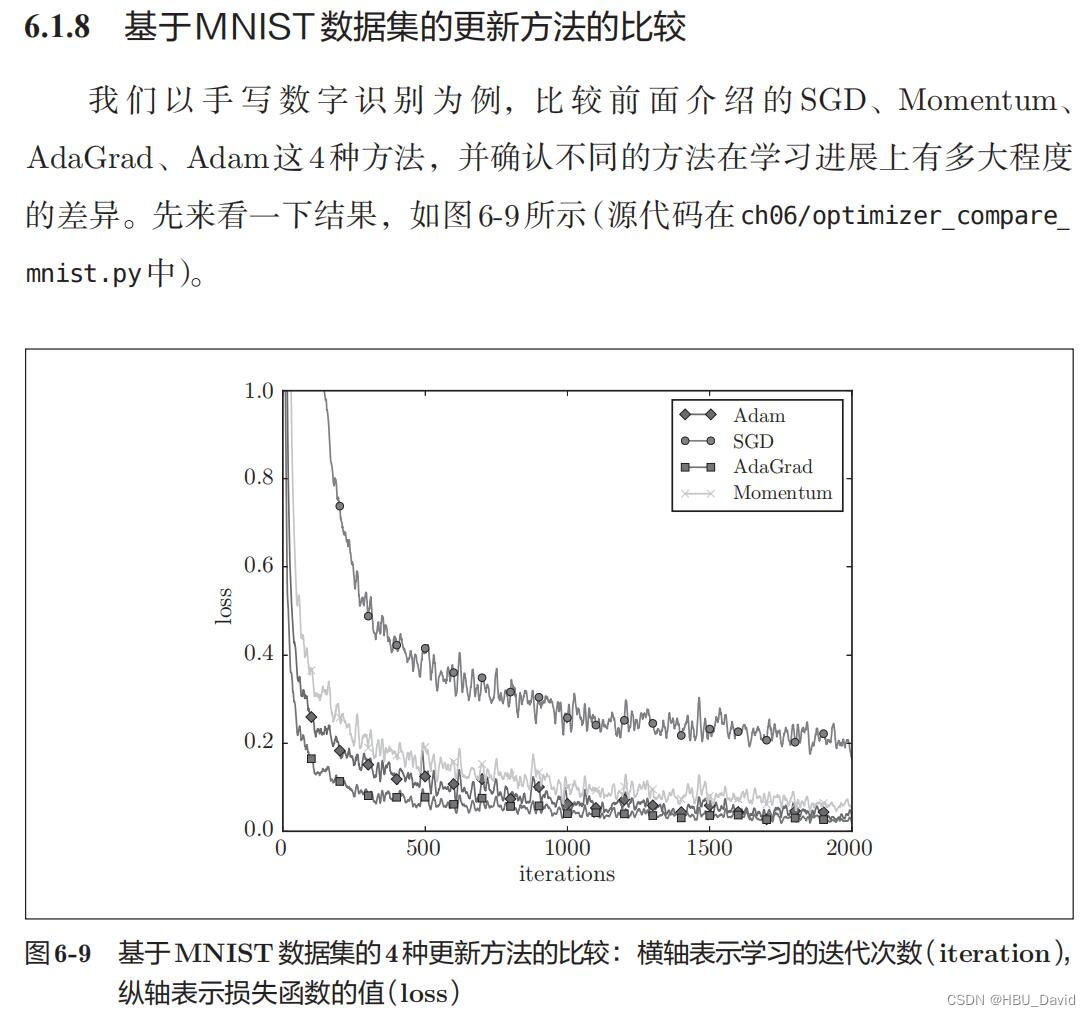
优化算法代码可参考前面的内容。

 MNIST数据集的更新方法的比较：

# coding: utf-8
import os
import sys
 
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *
 
# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
 
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
 
# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
# optimizers['RMSprop'] = RMSprop()
 
networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []
 
# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
 
    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)
 
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
 
    if i % 100 == 0:
        print("===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))
 
# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()

---

 总结

             首先，今天由于疫情好一点一点了，我们又搬了(哈哈哈)。

             其次，这次画了画图之后，真体会到了区别，包括和通过老师讲的，和之前学过的最优化联系起来了。

             其次，这次通过老师手写的代码，在好好看了之后，明白了之前上课的时候，学到的一些公式的含义。

             最后，感谢老师，感谢老师在学习和生活上的关心(哈哈哈)。