Transformer时间序列预测_transformer时序预测

介绍：

提示：Transformer-decoder

• 总体介绍
  本文将介绍一个 Transformer-decoder 架构，用于预测Woodsense提供的湿度时间序列数据集。该项目是先前项目的后续项目，该项目涉及在同一数据集上训练一个简单的 LSTM。人们认为 LSTM 在长序列上存在“短期记忆”问题。因此，该项目将使用一个 Transformer，它在同一数据集上优于之前的 LSTM 实现。
  

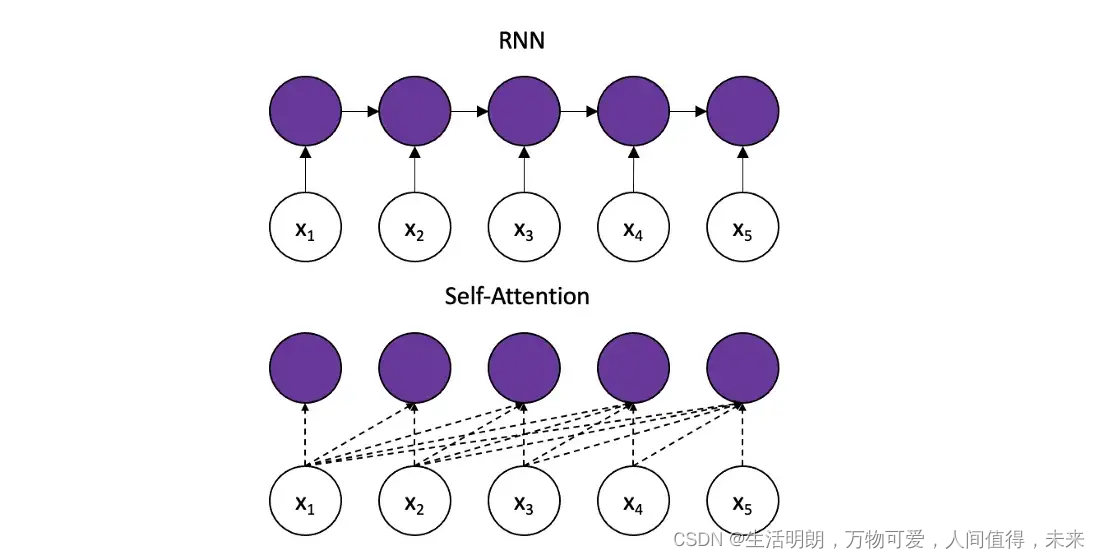
LSTM 按顺序处理标记，如上所示。该体系结构维护一个隐藏状态，该状态随每个新输入令牌更新，代表它所看到的整个序列。理论上，非常重要的信息可以在无限长的序列上传播。然而，在实践中，情况并非如此。由于梯度消失问题，LSTM 最终会忘记较早的标记。

相比之下，变形金刚保留与所有先前时间戳的直接连接，允许信息在更长的序列上传播。然而，这带来了新的挑战：模型将直接连接到爆炸式增长的输入量。为了从不重要的事物中过滤出重要的事物，变形金刚使用一种称为 自注意力的算法。

---

自注意力：

提示：这里可以添加要学的内容

在心理学中，注意力是将注意力集中在一种刺激上而排除其他刺激。同样，注意力机制旨在仅关注与完成给定任务相关的任意长序列中最重要的子集。¹

具体来说，模型必须决定先前标记中的哪些细节与编码当前标记相关。self-attention 块根据所有其他先前输入对每个新输入输入进行编码，根据与当前标记相关性的计算来确定焦点。下面提供了简要概述。

1.创建查询、键和值向量：
每个令牌生成关联的查询、键和值。将当前令牌的查询与所有其他令牌的键进行比较，以确定它们与当前令牌的相关性。值向量是给定标记的真实表示，用于创建新编码。在训练过程中，模型逐渐学习这三个权重矩阵，每个 token 乘以生成其对应的 key、query 和 value。
2.计算自注意力分数：
自注意力分数是当前标记与之前在序列中看到的任何其他标记之间的相关性的度量。它是通过计算当前标记的查询向量与被评分标记的键向量之间的点积来计算的。高分表示高相关性，而低分则相反。然后将分数通过 softmax 函数传递，这样它们都是正的并加到 1。在这一步中，自注意力分数可以看作是给予序列中标记的总关注度的百分比，在编码当前令牌。
3.相应地对当前标记进行编码：
在上一步中具有高 softmax 值的词应该对当前标记的编码贡献更大，而得分低的词应该贡献很小。为此，每个值向量都乘以它的 softmax 分数。这会保持原始值不变，但会根据其对当前标记的相对重要性来缩放整个向量。最后，将所有缩放后的值相加以生成当前标记的编码。
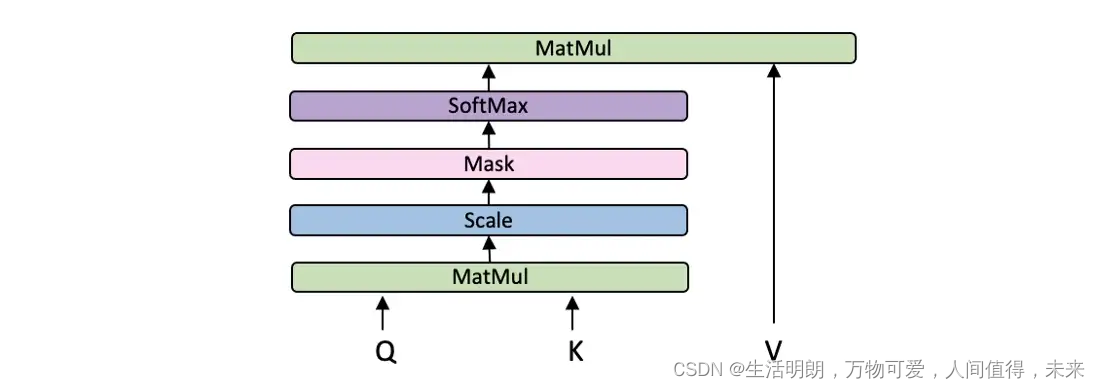由于这三个步骤由矩阵运算组成，因此可以优化如下：

---

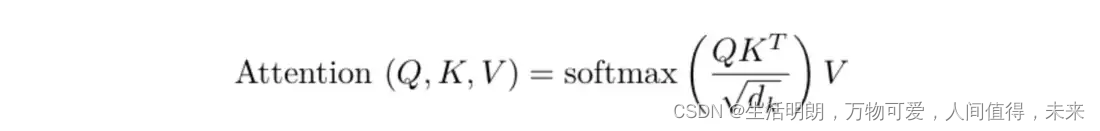
位置编码：

提示：位置编码

还有第二个挑战需要解决。时间序列不是按顺序处理的；因此，Transformer 本身不会学习时间依赖性。为了解决这个问题，必须将每个标记的位置信息添加到输入中。这样做时，self-attention 块将具有给定时间戳与当前时间戳之间相对距离的上下文，作为 self-attention 相关性的重要指标。

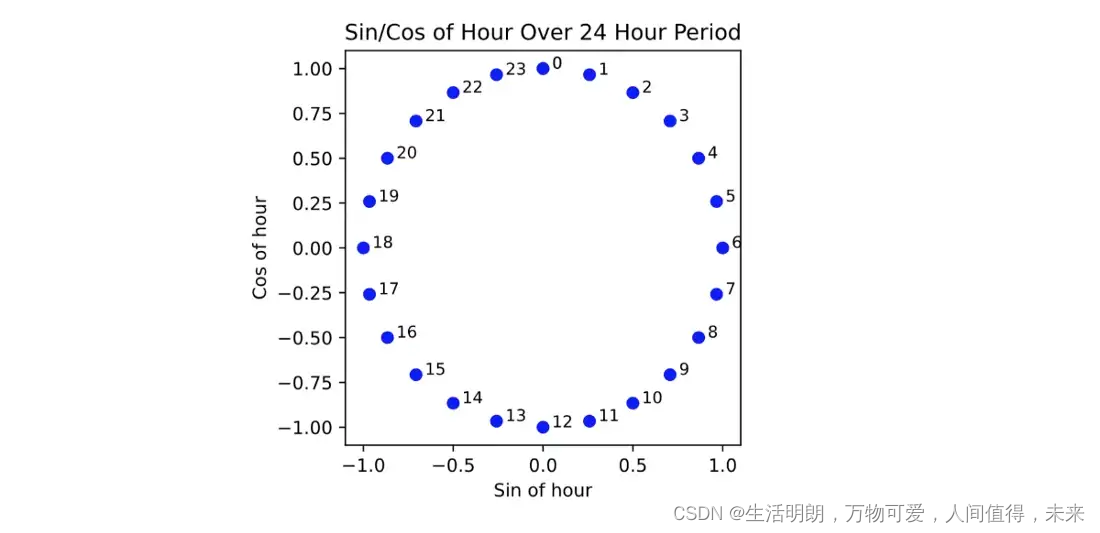
对于这个项目，位置编码实现如下：时间戳表示为三个元素——小时、日期和月份。为了真实地表示每种数据类型，每个元素都被分解为正弦和余弦分量。这样，十二月和一月在空间上很接近，就像月份在时间上很接近一样。同样的概念也适用于小时和天，因此所有元素都循环表示。

---

实现转换器解码器：

提示：这里统计学习计划的总量

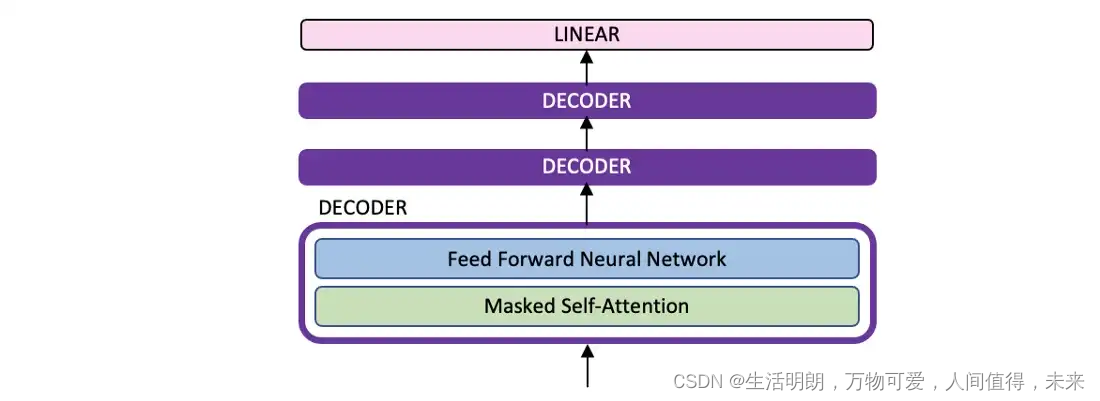
在 vanilla transformer 中，解码器由以下三个块组成：首先是一个 masked self-attention 块，然后是一个编码器-解码器块，最后是一个前馈块。本文的实现灵感来自GPT2 的decoder-only Transformer 实现，如下图所示。这些修改后的解码器块中的三个相互堆叠，将来自前一个块的编码作为输入传递到后续块。

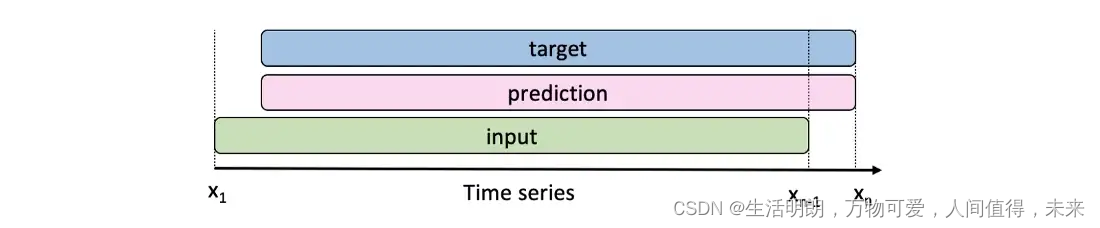
转换器的输入是一个给定的时间序列（单变量或多变量），如下面的绿色所示。然后目标是向右移动一次的序列，如下面的蓝色所示。也就是说，对于每个新输入，模型都会为下一个时间戳输出一个新的预测。

为了在长度为 5 的序列上表示这一点，对于第一个输入 x1，模型将输出其对即将到来的标记的预测：x2’。接下来，它被赋予真实的 x1 和 x2，并预测 x3’，等等。在每个新步骤中，它都会接收序列中所有先前的真实输入，以预测下一步。因此，模型的输出向量将是预测的标记 x2’、x3’、x4’、x5’、x6’。然后将其与真实值 x2、x3、x4、x5、x6 进行比较以训练模型，其中每个输出标记对损失的贡献相同。

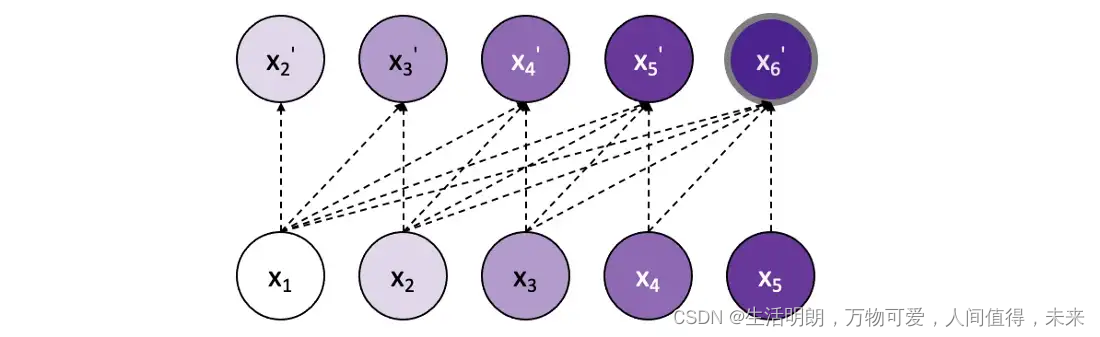
蒙面自我注意

要实现上面演示的模型，必须使用掩码来确保模型在每个步骤中只能访问序列中先出现的标记。具体来说，在应用 softmax 函数之前，当前正在关注的标记之后的所有标记都被屏蔽，以防止模型通过前瞻性作弊。当应用 soft-max 时，这些未来值的重要性将变为 0%，从而防止任何信息渗漏。

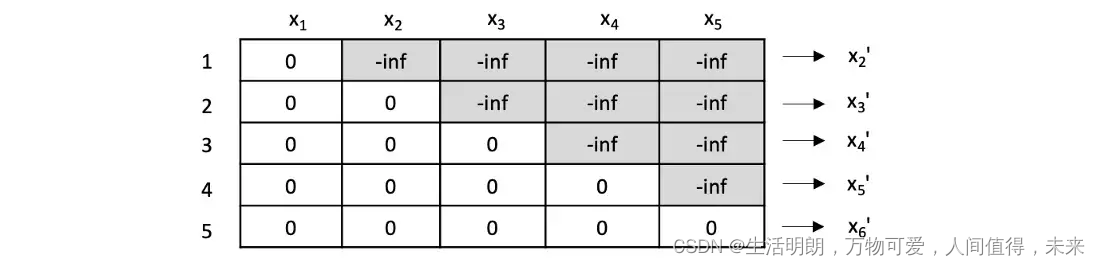
最后要注意的是，为简单起见，以上描述已经指出了计算中的顺序步骤。实际上，这些计算是在矩阵计算中同时进行的。

预定取样
在每个新步骤中为模型提供真实值而不是最后一个预测输出的概念称为教师强制。就像学生准备考试而老师在他身后看着一样，模型学习得很快，因为它的错误会立即得到纠正。换句话说，在得到纠正之前，它永远不会“偏离轨道太远”。²

teacher forcing 的缺点是，在每次新的预测中，模型可能会犯一些小错误，但无论如何它都会在下一步中获得真实值，这意味着这些错误永远不会对损失产生重大影响。该模型只需要学习如何提前预测一个时间步长。

然而，在推理过程中，模型现在必须预测更长的序列，不能再依赖频繁的修正。在每一步中，最后的预测被附加为下一步的新输入。因此，在推理过程中，训练期间并不严重的小错误很快就会在更长的序列中被放大。³在前面的类比中，这可以比作学生去参加考试，从来没有在没有老师帮助的情况下参加模拟考试他。

中的一个基本问题教师强迫出现：训练成为与推理截然不同的任务。为了弥合训练和推理之间的差距，模型需要慢慢学习纠正错误。因此，在训练和推理之间转换模型的任务就变成了逐渐为模型提供更多的预测输出，而不是真实值。

在早期阶段过快地进行推理——从模型的预测输出中抽样太多——会导致随机标记，因为模型还没有机会训练，从而导致收敛缓慢。另一方面，在最后几个时期没有足够快地进行推理——采样太少——将使训练和推理之间的差距太大，这意味着在训练期间表现良好的模型在推理期间的性能会急剧下降。

为了温和地弥合这一差距，使用了一种采样方法，其灵感来自 Bengio 的“使用递归神经网络进行序列预测的预定采样”。采样率随着时间的推移而演变，从最初选择真实值的高概率开始，就像在经典的教师强制中一样，然后逐渐收敛到纯粹从模型输出中采样，以模拟推理任务。论文中提出了不同的时间表，其中为该项目选择了逆 sigmoid 衰减。在这些最后的时期中，当模型连续采样其自身的许多预测值时，模型理想地学会了防止其小错误累积，因为它现在受到的惩罚要高得多。

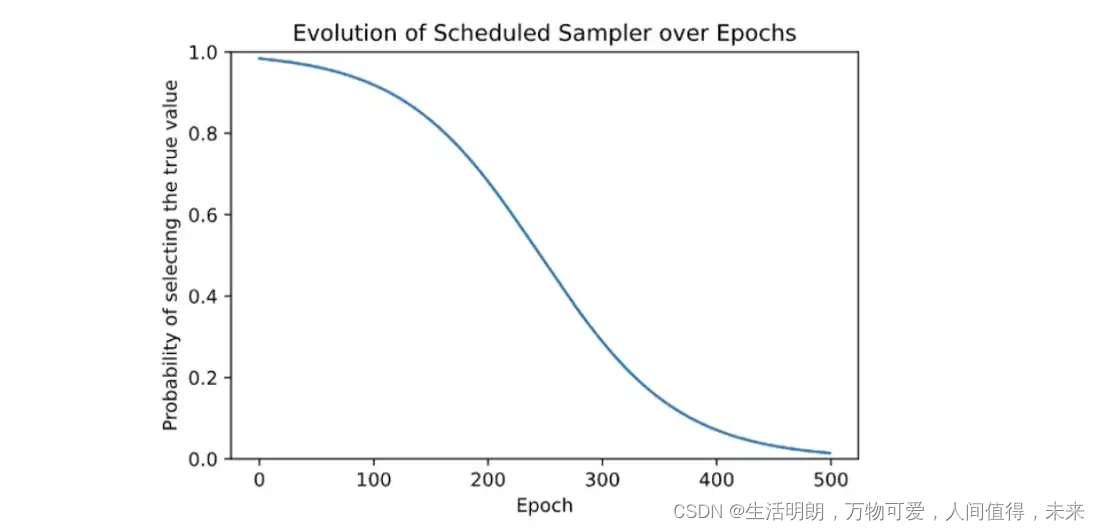
常数 k 用于微调反 S 型衰减图中的衰减率。
将此技术应用于模型会在 500 次训练中的第 310 次训练期间产生如下所示的结果。蓝点显示真实输入。红点表示选择作为下一步输入的值——无论是真实输入还是上一步的预测。绿点是模型的预测，仅将之前的红点作为输入。在第 310 轮，模型仅从真实输入中采样其值的 20%，其他 80% 是其自身建立的预测，如上面的逆 sigmoid 衰减图所示。可以看出，每次采样器再次选择真实输入时，模型都会“修正”。

例如，在时间戳 20 处，模型明显偏离轨道并预测湿度为 65%。采样器选择了真实的输出作为下一个输入，模型成功地在随后的时间戳 21 中几乎完美地自我校正。

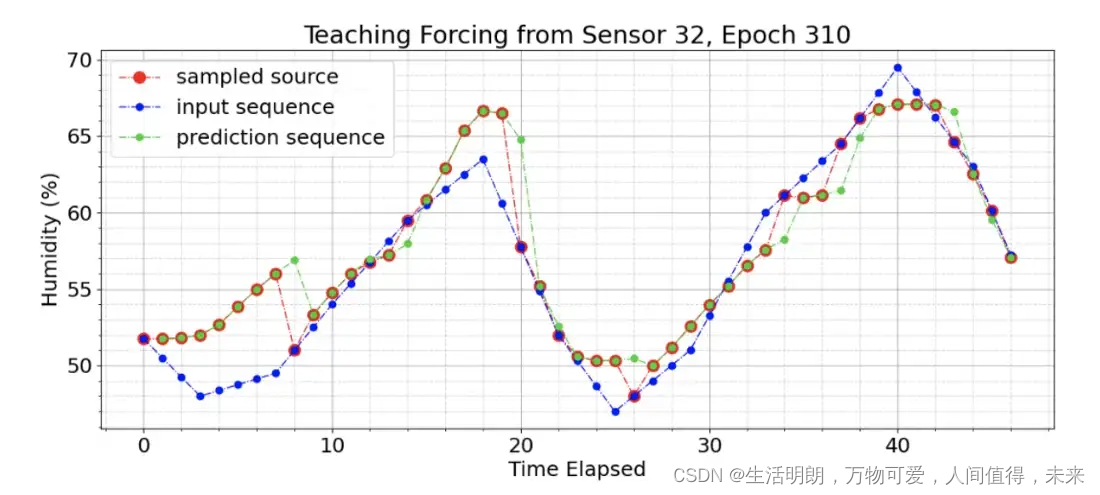
没有阈值的预定采样器
我们看到模型在序列的开头表现不佳。这是直观的，考虑到模型是在对特定序列知之甚少的情况下进行预测的。事实证明，使用在序列早期启动的预定采样器进行训练会混淆模型，因为在没有足够的输入来理解数据模式的情况下，它会因预测不佳而受到惩罚。为了纠正这个问题，在计划的采样器上设置了一个阈值，确保在计划的采样器以正常速率启动之前，前 24 个时间戳只使用真实值，代表一整天的数据，如逆 sigmoid 所示图，与时代相关。

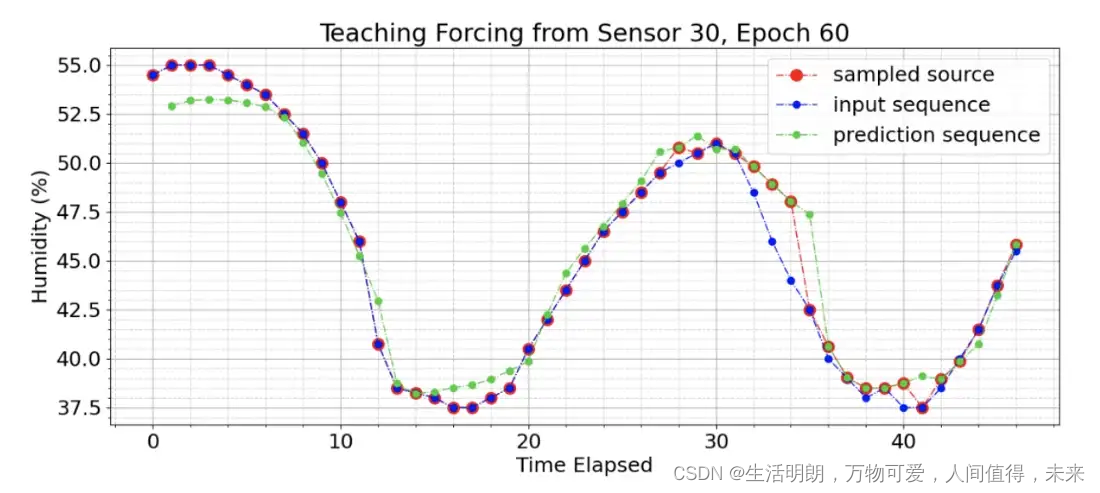
带阈值的预定采样器。前 24 个时间戳仅来自真实输入，与预定采样器设置的概率无关。
结果
如下所示，该模型成功地对 50 个时间戳的预测窗口进行了合理的预测。

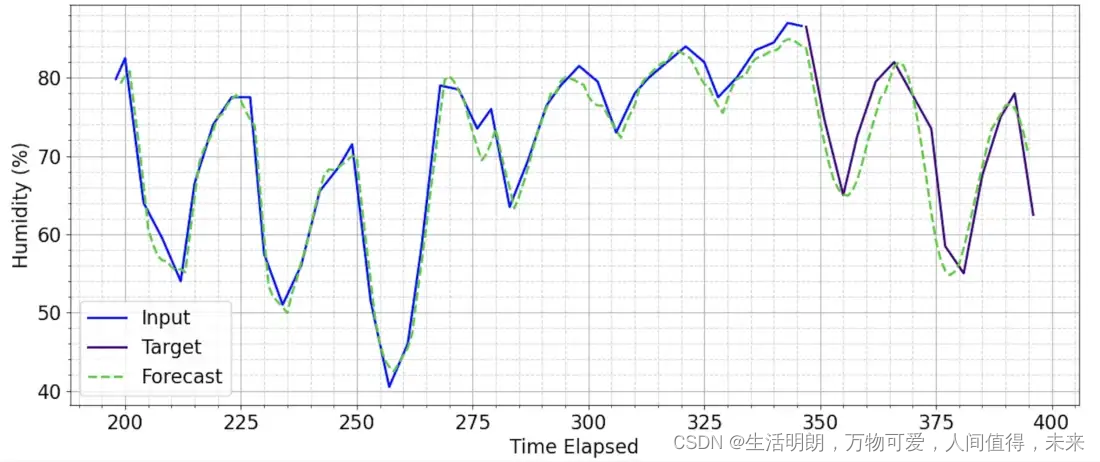
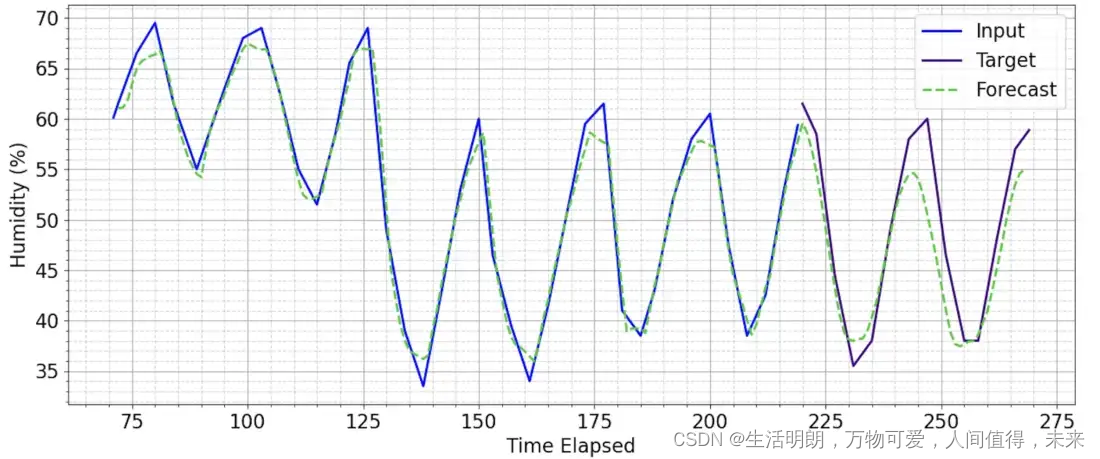
使用经过 500 轮训练的模型预测预测窗口为 50 的未见序列

使用经过 500 轮训练的模型预测预测窗口为 50 的未见序列
在它确实随着时间的推移偏离轨道的情况下，它会产生令人信服的预测，显示对数据的更深入理解。

使用经过 500 轮训练的模型预测预测窗口为 50 的未见序列

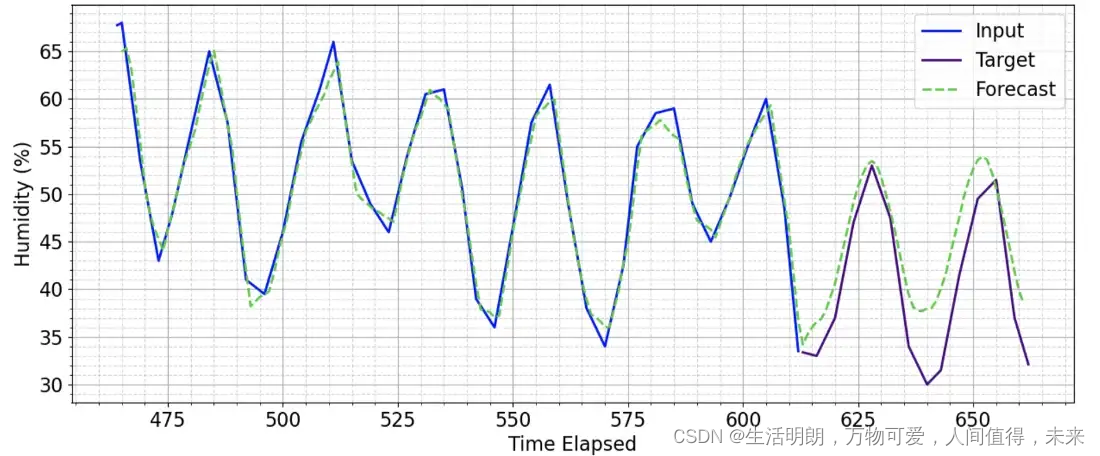
使用经过 500 轮训练的模型预测预测窗口为 50 的未见序列

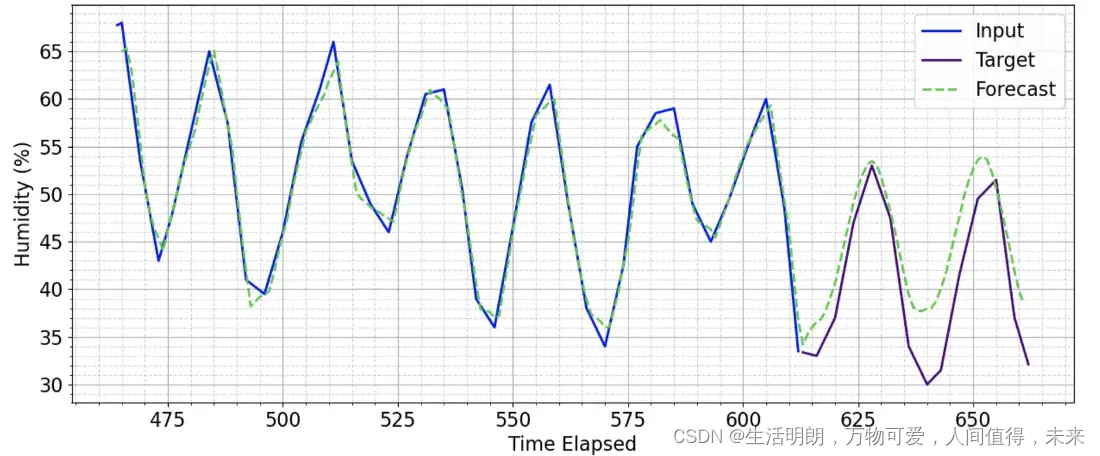
代码：https