- 18 神经网络及Python实现_神经网络设定随机w和b
- 2Python 深度学习第二版(GPT 重译)(一)
- 3MIT线性代数-方程组的几何解释
- 4DolpinScheduler2.0.5详细介绍与踩坑实战_dophischeduler
- 5mac安装nvm及换源及node安装切换_mac nvm 换源
- 6【已解决】labelme编辑label时,闪退;报错“IndexError: list index out of range”_labelme ai闪退
- 72023-12-17 AIGC-AnimateDiff详细安装和使用教程_animatediff_models
- 8CRC算法并行运算Verilog实现_crc verilog并行
- 9labelme汉化以及打包为.exe
- 10如何批量分别压缩大量大型文件 |7z 7zip cmd powershell RAR_7zip分别压缩多个文件
2022蓝桥杯C++B组国赛真题题解_2022拆分成10个整数
赞
踩
目录
A:2022
问题描述
将 2022 拆分成 10 个互不相同的正整数之和, 总共有多少种拆分方法?
注意交换顺序视为同一种方法, 例如 2022=1000+1022 和 1022+1000 就视为同一种方法。
答案提交
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
dp动态规划,a[i][j][v]代表1到i个数中,选j个数,和为v的答案总数;每次到i时有两种状况,选i和不选i
选i: a[i][j][v] =a[i-1][j-1][v-i]相对上次来说,j要加一,i要加一,但是此次选i因此要求上 一次 是v-i;
不选i: a[i][j][v] =a[i-1][j][v];
因此a[i][j][v] =a[i-1][j-1][v-i]+a[i-1][j][v];但是要考虑有时候i放不进去的情况,比如v=2,但i=5,i不能放因此递推公式有了
- #include <iostream>
- using namespace std;
- long long f[2030][11][2030];
- int main(){
- f[0][0][0]=1;
- for(int i=1;i<=2022;i++){
- for(int j=0;j<=10;j++){
- for(int v=0;v<=2022;v++){
- if(v - i >= 0 && j - 1 >= 0){
- f[i][j][v] = f[i - 1][j - 1][v - i];
- }
- f[i][j][v] += f[i - 1][j][v];
- }
- }
- }
-
-
- cout<<f[2022][10][2022];
- return 0;
- }
B:钟表
问题描述
在 12 小时制的钟表中, 有分针、时针、秒针来表示时间。记分针和时 针之间的夹角度数为 A(0≤A≤180) 、分针和秒针之间的夹角度数为 (0≤B≤180)。而恰好在 s 时 f 分 m 秒时, 满足条件 A=2B 且 0≤f<60;0≤m<60, 请问 s,f,m 分别是多少。
请你找出一个 0 时 0 分 0 秒以外的解。
注意时针、分针、秒针都围绕中心匀速转动。
提交格式为三个由一个空格隔开的整数, 分别表示 s,f,m 。如 3 11 58 表示 3 点 11 分 58 秒。
答案提交
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为三个由一个空格隔开的整数, 在提交答案时只填写为三个由一个空格隔开的整数, 填写多余的内容将无法得分。
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
角度?我们把角度看为比例,比如30秒就是30/60=0.5,然后模拟就行了
- #include <iostream>
- #include <cmath>
- using namespace std;
- int main(){
- for(int h=0;h<=6;h++){
- for(int fen=0;fen<60;fen++){
- for(int miao=0;miao<60;miao++) {
- double miaoj=miao/60.00000;
- double fenj=fen/60.00000+(miao/60.00000)/60.000000;
- double hj= h/12.000000+(fen+miao/60.00000)/(12*60.00000);
- double a=fabs(fenj-hj);
- if(a>0.5) a=1-a;
- double b=fabs(fenj-miaoj);
- if(b>0.5) b=1-b;
- if(fabs(a-2*b)<=1e-8 && h!=0){
- cout<<h<<' '<<fen<<' '<<miao;
- }
- }
-
- }
- }
- return 0;
- }
C:卡牌
问题描述
这天, 小明在整理他的卡牌。
他一共有 n 种卡牌, 第 i 种卡牌上印有正整数数 i(i∈[1,n]), 且第 i 种卡牌 现有 ai 张。
而如果有 n 张卡牌, 其中每种卡牌各一张, 那么这 n 张卡牌可以被称为一 套牌。小明为了凑出尽可能多套牌, 拿出了 m 张空白牌, 他可以在上面写上数 ii, 将其当做第 i 种牌来凑出套牌。然而小明觉得手写的牌不太美观, 决定第 ii 种牌最多手写 bi 张。
请问小明最多能凑出多少套牌?
输入格式
输入共 3 行, 第一行为两个正整数 n,m 。
第二行为 nn 个正整数 a1,a2,…,an 。
第三行为 nn 个正整数 b1,b2,…,bn 。
输出格式
一行, 一个整数表示答案。
样例输入
- 4 5
- 1 2 3 4
- 5 5 5 5
样例输出
3
样例说明
这 5 张空白牌中, 拿 2 张写 1 , 拿 1 张写 2 , 这样每种牌的牌数就变为了3,3,3,4, 可以凑出 3 套牌, 剩下 2 张空白牌不能再帮助小明凑出一套。
评测用例规模与约定
对于 30% 的数据, 保证 0n≤2000;
对于 100% 的数据, 保证 ai,bi≤2n;m≤n2 。
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
暴力解法:
- #include <iostream>
- using namespace std;
- int n,m;
- long long a[200005];
- long long b[200005];
- long long ans;
- int main(){
- long long min=1e16;
- cin>>n>>m;
- for(int i=0;i<n;i++){
- cin>>a[i];
- if(min>a[i]){
- min=a[i];
- }
- }
- for(int i=0;i<n;i++){
- cin>>b[i];
- }
- ans=min;
- for(int i=0;i<n;i++){
- a[i]=a[i]-min;
- }
- while(1){
- for(int i=0;i<n;i++){
- if(a[i]==0){
- if(b[i]>0&&m>0) {
- m--;
- b[i]--;
- a[i]++;
-
- }else{
- cout<<ans;
- return 0;
- }
- }
- if(i==n-1){
- ans++;
- }
- a[i]--;
-
- }
- }
- cout<<ans;
- return 0;
- }

二分法:
- #include<iostream>
- #include<algorithm>
- using namespace std;
-
-
- long long n,m,l,r;
- long long a[200005];
- long long b[200005];
- long long kk;
-
- bool check(long long x){
- long long s = 0;
- for (int i = 0; i < n; i++) { //判断x套牌可以凑出来不
- if (x - a[i] <= b[i]) {
- s += max(x - a[i],kk );
- }
- else return false;
- }
- if (s <= m) return true;
- return false;
- }
-
- int main(){
- cin>>n>>m;
- for(int i=0;i<n;i++){ //输入,以最小值为左指针
- cin>>a[i];
- l = min(l, a[i]);
- }
- for(int i=0;i<n;i++){
- cin>>b[i];
- r=max(r,a[i]+b[i]); //以可以达到的最大数目为右指针
- }
- int ans;
- while(l<=r){
- long long mid=(l+r)/2; //二分查找可以凑成几套牌
- if(check(mid)){
- ans=mid;
- l=mid+1;
- }else{
- r=mid-1;
- }
- }
- cout<<ans<<endl;
- return 0;
- }
D:最大数字
问题描述
给定一个正整数 N 。你可以对 N 的任意一位数字执行任意次以下 2 种操 作:
-
将该位数字加 1 。如果该位数字已经是 9 , 加 1 之后变成 0 。
-
将该位数字减 1 。如果该位数字已经是 0 , 减 1 之后变成 9 。
你现在总共可以执行 1 号操作不超过 A 次, 2 号操作不超过 B 次。 请问你最大可以将 NN 变成多少?
输入格式
第一行包含 3 个整数: N,A,B 。
输出格式
一个整数代表答案。
样例输入
123 1 2
样例输出
933
样例说明
对百位数字执行 2 次 2 号操作, 对十位数字执行 1 次 1 号操作。
评测用例规模与约定
对于 30% 的数据, 0≤A,B≤10
对于 100% 的数据, 0≤A,B≤100
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
- #include <iostream>
- #include <cmath>
- using namespace std;
- string n;
- long long ans;
- int a,b;
- void dfs(int x,long long an){ //a代表每次遍历的数
- int t=n[x]-'0'; //位数转为int
- if(n[x]){ //防止为空
- int c=min(a,9-t);
- a-=c;
- dfs(x+1,an*10+t+c);
- a+=c;
- if(b>t){
- b=b-t-1;
- dfs(x+1,an*10+9);
- b=b+t+1;
- }
- }else{
- ans=max(ans,an);
- }
- }
- int main(){
- cin>>n>>a>>b;
- dfs(0,0); //0号字符
-
- cout<<ans;
- return 0;
- }

E:出差
问题描述
A 国有 N 个城市, 编号为 1…N 。小明是编号为 1 的城市中一家公司的员 工, 今天突然接到了上级通知需要去编号为 N 的城市出差。
由于疫情原因, 很多直达的交通方式暂时关闭, 小明无法乘坐飞机直接从 城市 1 到达城市 N, 需要通过其他城市进行陆路交通中转。小明通过交通信息 网, 查询到了 M 条城市之间仍然还开通的路线信息以及每一条路线需要花费的 时间。
同样由于疫情原因, 小明到达一个城市后需要隔离观察一段时间才能离开 该城市前往其他城市。通过网络, 小明也查询到了各个城市的隔离信息。(由于 小明之前在城市 1 , 因此可以直接离开城市 1 , 不需要隔离)
由于上级要求, 小明希望能够尽快赶到城市 N, 因此他求助于你, 希望你 能帮他规划一条路线, 能够在最短时间内到达城市 N 。
输入格式
第 1 行: 两个正整数N,M,N 表示 A 国的城市数量, M 表示末关闭的路 线数量
第 2 行: N 个正整数, 第 i 个整数 Ci 表示到达编号为i 的城市后需要隔离 的时间
第 3 …M+2 行: 每行 3 个正整数,u,v,c, 表示有一条城市 uu 到城市 v的 双向路线仍然开通着, 通过该路线的时间为 c
输出格式
第 1 行: 1 个正整数, 表示小明从城市 1 出发到达城市 N 的最短时间(到 达城市 N, 不需要计算城市 N 的隔离时间)
样例输入
- 4 4
- 5 7 3 4
- 1 2 4
- 1 3 5
- 2 4 3
- 3 4 5
样例输出
13
样例说明

评测用例规模与约定
对于 100% 的数据, 1≤N≤1000,1≤M≤10000,1≤Ci≤200,1≤u,v≤ N,,1≤c≤1000
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
最短路径采用Dijkstra算法会快一点;
- #include <iostream>
- #include <cstring>
- #include <cmath>
- using namespace std;
- int n,m; //n个城市,m条路线
- int geli[10005]; //到每个城市的隔离时间
- int luxian[10005][10005];
- int juli[10005]; //到一点的最短距离
- bool vis[10005];
- int dj(){
- memset(juli,0x3f3f3f3f,sizeof(juli));
- juli[1]=0; //距离起点为0
- geli[1]=0; //出自己城市不隔离
- geli[n]=0; //到达终点不需要隔离
- for(int i=1;i<=n;i++){ //剔除n个
- int s=-1;
- for(int j=1;j<=n;j++){
- if(!vis[j]&&((s==-1)||(juli[j]<juli[s]))){
- s=j; //第一次s为1,之后每一次寻找与前一个想通的城市
- }
- }
- vis[s]=1;
- for(int j=1;j<=n;j++){
-
- juli[j]=min(juli[j],juli[s]+luxian[s][j]+geli[s]);
-
- }
- }
- return juli[n];
- }
- int main(){
- cin>>n>>m;
- for(int i=1;i<=n;i++){
- cin>>geli[i];
- }
- memset(luxian,0x3f3f3f3f,sizeof(luxian)); //无穷大
- for(int i=1;i<=n;i++){
- luxian[i][i]=0; //自己到自己为0
- }
- for(int i=0;i<m;i++){
- int a,b,c;
- cin>>a>>b>>c;
- luxian[a][b]=luxian[b][a]=min(c,luxian[a][b]);
- }
- int ans=dj();
- cout<<ans;
- return 0;
- }
-
F:费用报销
问题描述
小明在出差结束后返回了公司所在的城市, 在填写差旅报销申请时, 粗心 的小明发现自己弄丢了出差过程中的票据。
为了弥补小明的损失, 公司同意小明用别的票据进行报销, 但是公司财务 要求小明提交的票据中任意两张的日期差不小于 K 天, 且总金额不得超过实际 差旅费用 M 。
比如财务要求 K=7 时, 若小明提交了一张 1 月 8 日的票据, 小明就不能 提交 1 月 2 日至 1 月 14 日之间的其他票据, 1 月 1 日及之前和 1 月 15 日及之 后的票据则可以提交。
公司的同事们一起给小明凑了 N 张票据, 小明现在想要请你帮他整理一 下, 从中选取出符合财务要求的票据, 并使总金额尽可能接近 M 。
需要注意, 由于这些票据都是同一年的, 因此 12 月底的票据不会影响到 1 月初票据的提交。这一年不是闰年。
输入格式
第 1 行: 3 个整数, N,M,K
第 2…N+1 行: 每行 3 个整数 mi,di,vi, 第 i+1 行表示第 i 张票据时间 的月份 mi 和日期 di,vi 表示该票据的面值
输出格式
第 1 行: 1 个整数, 表示小明能够凑出的最大报销金额
样例输入
- 4 16 3
- 1 1 1
- 1 3 2
- 1 4 4
- 1 6 8
样例输出
10
样例说明
选择 1 月 3 日和 1 月 6 日的票据
评测用例规模与约定
对于 100% 的评测用例, 1≤N≤1000,1≤M≤5000,1≤K≤50,1≤mi≤ 12,,1≤di≤31,1≤vi≤400
日期保证合法。
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
动态规划问题, 先将n张票据以结构体保存下来,然后转化为数组,但是一天可能有好几张票据,因此我们要将一天票据进行比较。然后利用递推公式:
选i票据:ans[i] ans[i-k]+面值[i] 前提小于等于m'
不选i票据:ans[i] ans[i-1]
因此:ans[i]=max(ans[i-k]+面值[i],ans[i-1])
然后就是在于一天中每个票据挨个比较
- #include <iostream>
- #include <vector>
- #include <cmath>
- using namespace std;
- int n,m,k; //n代表n个票据,m钱,k天
- int piao1[400];
- int ans[500];
- vector<int> piao2[400];
- int month12[12]={31,28,31,30,31,30,31,31,30,31,30,31};
- struct piao{
- int month;
- int day;
- int qian;
- };
- piao a[1005];
- int getday(int x,int y){
- int ans=y;
- for(int i=0;i<x-1;i++){
- ans+=month12[i];
- }
- return ans;
- }
- int main(){
- cin>>n>>m>>k;
- for(int i=1;i<=n;i++){
- cin>>a[i].month>>a[i].day>>a[i].qian;
- } //输入结构体
- int daymax=0;
- for(int i=1;i<=n;i++){
- int day=getday(a[i].month,a[i].day);
- if(piao1[day]){
- piao2[day].push_back(a[i].qian);
- }else{
- piao1[day]=a[i].qian;
- }
- daymax=max(day,daymax); //全转为天数,重合的装在vector里
- }
-
- for(int i=1;i<=daymax;i++){ //遍历每天的票据
- if(piao1[i]==0) {
- ans[i]=ans[i-1]; //这一天没有票,等于上一天的值
- }else{
- if(piao2[i].size()==0){ //这一天只有一张票
- if(ans[i-1]<=m){
- ans[i]=ans[i-1];
- }
- if(ans[i-k]+piao1[i]<=m){
- ans[i]=max(ans[i],ans[i-k]+piao1[i]);
- }
- }else{
- if(ans[i-1]<=m){
- ans[i]=ans[i-1]; //这一天有多张票
- }
- if(ans[i-k]+piao1[i]<=m){
- ans[i]=max(ans[i],ans[i-k]+piao1[i]);
- }
- int len=piao2[i].size();
- for(int j=0;j<len;j++){
- if(ans[i-k]+piao2[i][j]<=m){
- ans[i]=max(ans[i],ans[i-k]+piao2[i][j]);
- }
- }
- }
- }
- }
- cout<<ans[daymax];
- return 0;
- }

G:故障
问题描述
在软件或系统开发中, 我们会遇到各种各样的故障。为了从故障现象反推 故障原因, 工程师们会总结一种叫做相关性矩阵的二维表格, 来表示故障原因 与故障现象之间的关系。比如:

其中每行表示一种故障原因, 每一列表示一种故障现象。该矩阵表示故障 原因 AA 可能产生故障现象 2、3、4, 故障原因 BB 可能产生故障现象 1、3。
在实际开发过程中, 如果出现了故障原因, 工程师就可以根据故障现象, 去计算每种故障原因产生的概率, 并按照概率大小对故障原因进行排查, 以达 到快速定位故障原因的目的。
现在, 我们假设系统开发中同一时间只会出现一种故障原因, 并且故障原 因引起各故障现象是独立事件。举个例子来说:
假设系统现在发生了故障原因 A, 有 1/3的概率出现故障现象 2 , 有 1/4 的概 率出现故障现象 3 , 有 1/2的概率出现故障现象 4。由于 3 种现象是独立发生的, 因此有 1/3*1/4*1/2 的概率同时出现故障 2、3、4。
约定若相关性矩阵中没有 ' x ' 记号, 则表示该故障原因一定不会产生某故 障现象, 比如故障原因 A, 一定不会产生故障现象 1。
根据历史经验数据, 我们统计得到了每一种故障原因出现的概率以及每一 种故障原因对应的故障现象产生概率。
现在已知系统出现的故障现象, 求问各个故障原因发生的概率。
输入格式
第 1 行: 2 个正整数 N,M,N 表示故障原因的个数(编号 1…N ), M 表 示故障现象的个数 (编号 1 1…M)
第 2 行: N 个整数, 第 i 个数表示故障原因 i 产生的概率 Pi.
第 3…N+2 行: 每行 M 个整数, 第 i+2 行第 j 个整数 Pij 表示故障原 因 i 出现故障现象 j 的概率 (百分比).
第 N+3 行: 1 个正整数 K, 表示目前出现的故障现象数量
第 N+4 行: K 个正整数, 依次为当前出现的故障现象编号, 不会重复
输出格式
第 1…N 行: 按概率从高到低输出每种故障原因及其可能的概率, 若出现 概率相同则优先输出编号小的故障原因。第 1 个数为故障原因编号, 第 2 个数 为故障概率 (百分比), 保留 2 位小数。
样例输入
- 3 5
- 30 20 50
- 0 50 33 25 0
- 30 0 35 0 0
- 0 0 0 25 60
- 1
- 3
样例输出
- 2 56.89
- 1 43.11
- 3 0.00
评测用例规模与约定
对于所有测试用例, 1≤N≤40,1≤M≤20,0≤Pi≤100,Σ(Pi)=100, 0≤Pij≤100,
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
这个题敢不敢再写得长一点,看题目半小时过去了,概率题;
就是这个算法,概率论的题,还好我们开过这门课,呜呜呜呜呜。
- #include <iostream>
- #include <stdio.h>
- #include <algorithm>
- #include <cmath>
- using namespace std;
- int n,m; //n行,m列
- int yuanyin[450];
- int p1[450][450];
- int k;
- int guzhang[4500];
- int vis2[450];
- int vis1[450];
- double dange[450];
- int id[450];
- bool cmp(int a,int b){
- if(fabs(dange[a]-dange[b])>1e-8){
- return dange[a]>dange[b]; //当不相等时返回大的,否则返回id值小的
- }else{
- return a<b;
- }
- }
- int main(){
- cin>>n>>m;
- for(int i=1;i<=n;i++){
- cin>>yuanyin[i];
- }
- for(int i=1;i<=n;i++){
- for(int j=1;j<=m;j++){
- cin>>p1[i][j];
- }
- }
- cin>>k;
- for(int i=1;i<=k;i++){
- cin>>guzhang[i];
- vis1[guzhang[i]]=1; //标记故障
- }
- double num=0;
- for(int i=1;i<=n;i++){
- dange[i]=1; //便于乘
- for(int j=1;j<=m;j++){
- if(vis1[j]){ //此点是故障点
- dange[i]=(double)dange[i]*p1[i][j]/100.0;
- }else{
- dange[i]=(double)dange[i]*(100-p1[i][j])/100.0;
- }
- }
- dange[i]=(double)dange[i]*yuanyin[i]/100.0;
- num+=dange[i];
- }
- if(fabs(num)<1e-9){
- for(int i = 1 ; i <= n ; i ++){
- printf("%lld 0.00\n" , i) ;
- }
- return 0 ;
- }
-
- for(int i=1;i<=n;i++){ //很巧妙的排序,对id排序,然后输出
- id[i]=i;
- dange[i]=dange[i]*100.0/num;
- }
- sort(id+1,id+1+n,cmp); //根据dange的值排id
- for(int i=1;i<=n;i++){
- printf("%lld %0.2lf\n",id[i],dange[id[i]]);
- }
- return 0;
- }

H:机房
问题描述
这天, 小明在机房学习。
他发现机房里一共有 n 台电脑, 编号为 1 到 n, 电脑和电脑之间有网线连 接, 一共有 n−1 根网线将 n 台电脑连接起来使得任意两台电脑都直接或者间 接地相连。
小明发现每台电脑转发、发送或者接受信息需要的时间取决于这台电脑和 多少台电脑直接相连, 而信息在网线中的传播时间可以忽略。比如如果某台电脑 用网线直接连接了另外 d 台电脑, 那么任何经过这台电脑的信息都会延迟 d 单 位时间 (发送方和接收方也会产生这样的延迟, 当然如果发送方和接收方都是 同一台电脑就只会产生一次延迟)。
小明一共产生了 m 个疑问: 如果电脑 ui 向电脑 vi 发送信息, 那么信息从 ui 传到 vi 的最短时间是多少?
输入格式
输入共 n+m 行, 第一行为两个正整数 n,m 。
后面 n−1 行, 每行两个正整数 x,y 表示编号为 x 和 y 的两台电脑用网线 直接相连。
后面 mm 行, 每行两个正整数 ui,vi 表示小明的第i 个疑问。
输出格式
输出共 m 行, 第 i 行一个正整数表示小明第 ii 个疑问的答案。
样例输入
- 4 3
- 1 2
- 1 3
- 2 4
- 2 3
- 3 4
- 3 3
样例输出
- 5
- 6
- 1
样例说明
这四台电脑各自的延迟分别为 2,2,1,1 。
对于第一个询问, 从 2 到 3 需要经过 2,1,3, 所以时间和为 2+2+1=5 。
对于第二个询问, 从 3 到 4 需要经过 3,1,2,4, 所以时间和为 1+2+2+1=6。
对于第三个询问, 从 3 到 3 只会产生一次延迟, 所以时间为 1 。
评测用例规模与约定
对于 30% 的数据, 保证n,m≤1000;
对于 100% 的数据, 保证n,m≤100000 。
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
小编这题只会偏偏分,AC需要LCA加DFS加树的前缀和。我们看看大佬的代码吧,大体就是建一个数,统计每个节点到根节点的延时,然后通过LCA寻找询问两个点的最近公共祖先,算出最小延时。
- #include<bits/stdc++.h>
- using namespace std;
- typedef long long LL;
- typedef pair<int,int> PII;
- const int N=100010;
-
- unordered_map<int,vector<int>> gra;
- int n,m;
- //单个点的出度
- int d[N];
- //记录点i到根节点的延迟
- int w[N];
- //并查集数组
- int q[N];
- //记录答案
- int res[N];
- int st[N];
- //存下查询
- vector<PII> query[N];
- //并查集查询
- int find(int x){
- if(x!=q[x]) q[x]=find(q[x]);
- return q[x];
- }
-
- void dfs(int u,int fa)
- {
- w[u]+=d[u];
- for(auto g:gra[u]){
- if(g==fa) continue;
- w[g]+=w[u];
- dfs(g,u);
- }
- }
-
- void tarjan(int u)
- {
- st[u]=1;
- for(auto j:gra[u]){
- if(!st[j])
- {
- tarjan(j);
- q[j]=u;
- }
- }
- for(auto item: query[u]){
- int y=item.first,id=item.second;
- if(st[y]==2){
- int anc=find(y);
- res[id]=w[y]+w[u]-w[anc]*2+d[anc];
- }
- }
- st[u]=2;
- }
- int main()
- {
- cin>>n>>m;
- for(int i=0;i<n-1;++i){
- int a,b;
- scanf("%d%d",&a,&b);
- gra[a].push_back(b);
- gra[b].push_back(a);
- d[a]++,d[b]++;
- }
- for(int i=0;i<m;++i){
- int a,b;
- scanf("%d%d",&a,&b);
- if(a!=b){
- query[a].push_back({b,i});
- query[b].push_back({a,i});
- }else{
- res[i]=d[a];
- }
- }
- dfs(1,-1);
- for(int i=1;i<=n;++i) q[i]=i;
- tarjan(1);
- for(int i=0;i<m;++i) printf("%d\n",res[i]);
- return 0;
- }
I:齿轮
问题描述
这天, 小明在组装齿轮。
他一共有 n 个齿轮, 第 i 个齿轮的半径为 ri, 他需要把这 n 个齿轮按一定 顺序从左到右组装起来, 这样最左边的齿轮转起来之后, 可以传递到最右边的 齿轮, 并且这些齿轮能够起到提升或者降低转速 (角速度) 的作用。
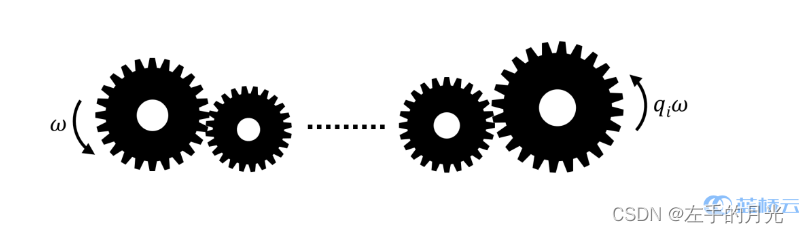
小明看着这些齿轮, 突然有 QQ 个疑问:能否按一定顺序组装这些齿轮使得 最右边的齿轮的转速是最左边的齿轮的 qi 倍?
输入格式
输入共 Q+2 行, 第一行为两个正整数 n,Q, 表示齿轮数量和询问数量。 第二行为 n 个正整数 r1,r2,…,rn, 表示每个齿轮的半径。
后面 Q 行, 每行一个正整数 qi 表示询问。
输出格式
Q 行, 对于每个询问, 如果存在至少一种组装方案满足条件, 输出 'YES', 否则输出 'NO '。
样例输入
- 5 3
- 4 2 3 3 1
- 2
- 4
- 6
样例输出
- YES
- YES
- NO
样例说明
询问 1 方案之一 : 23341
询问 2 方案之一:42331
询问 3 没有方案
评测用例规模与约定
对于 15% 的数据, 保证 n,Q≤100;
对于 30% 的数据, 保证 n,Q≤2000;
对于100% 的数据, 保证 n,Q≤2×105;ri,qi≤2×105 。
运行限制
| 语言 | 最大运行时间 | 最大运行内存 |
|---|---|---|
| C++ | 1s | 256M |
| C | 1s | 256M |
| Java | 3s | 256M |
| Python3 | 5s | 256M |
暴力做法:
- #include <iostream>
- #include <algorithm>
-
- using namespace std;
-
-
- int n,q;
- int banjing[200005];
- int xunwen[200005];
- bool st[200005];
- int main(){
- cin>>n>>q;
- for(int i=1;i<=n;i++){
- cin>>banjing[i];
- }
- for(int i=1;i<=q;i++){
- cin>>xunwen[i];
- }
- sort(banjing,banjing+n+1);
- int len=0;
- for(int i=1;i<=n;i++){
- for(int j=i+1;j<=n;j++){
- if(banjing[j]%banjing[i]==0){
- int b=banjing[j]/banjing[i];
- st[b]=1;
- len++;
- }
- }
- }
- for(int i=1;i<=q;i++){
- if(n==1&&xunwen[i]==1){
- cout<<"YES"<<endl;
- }else if(st[xunwen[i]]){
- cout<<"YES"<<endl;
- }else{
- cout<<"NO"<<endl;
- }
- }
- return 0;
- }

寻找因式:
- #include <iostream>
- #include <algorithm>
- #include <unordered_set>
- using namespace std;
- unordered_set<int> s;
- int n,q;
- int banjing[200005];
- bool st[200005];
- int main(){
- ios_base::sync_with_stdio(false); //提高cin和cout效率
- cin.tie(0);
- cin>>n>>q;
- for(int i=1;i<=n;i++){
- cin>>banjing[i];
- }
- sort(banjing,banjing+n+1);
-
- for(int i=1;i<=n;i++){
- int v=banjing[i];
- for(int j=1;j*j<=v;j++){
- if(v%j==0){
- if(s.find(j)!=s.end()){
- st[v/j]=1;
- }
- if(s.find(v/j)!=s.end()){
- st[j]=1;
- }
- }
- }
- s.insert(banjing[i]);
- }
- for(int i=1;i<=q;i++){
- int xunwen;
- cin>>xunwen;
- if(n==1&&xunwen==1){
- cout<<"YES"<<'\n';
- }else if(st[xunwen]){
- cout<<"YES"<<'\n';
- }else{
- cout<<"NO"<<'\n';
- }
- }
- return 0;
- }
J:搬砖
问题描述
这天,小明在搬砖。
他一共有 n 块砖, 他发现第 i 砖的重量为 wi, 价值为 vi 。他突然想从这些 砖中选一些出来从下到上堆成一座塔, 并且对于塔中的每一块砖来说, 它上面 所有砖的重量和不能超过它自身的价值。
他想知道这样堆成的塔的总价值(即塔中所有砖块的价值和)最大是多少。
输入格式
输入共 n+1 行, 第一行为一个正整数 nn, 表示砖块的数量。
后面 n 行, 每行两个正整数 wi,vi 分别表示每块砖的重量和价值。
输出格式
一行, 一个整数表示答案。
样例输入
- 5
- 4 4
- 1 1
- 5 2
- 5 5
- 4 3
样例输出
10
样例说明
选择第 1、2、4 块砖, 从上到下按照2、1、4 的顺序堆成一座塔, 总价值 为 4+1+5=10
评测用例规模与约定
对于 20% 的数据, 保证 n≤10;
对于 100% 的数据, 保证n≤1000;wi≤20;vi≤20000 。
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
排序后,背包动态规划
- #include <iostream>
- #include <algorithm>
- using namespace std;
- int n;
- int w;
- int ans;
- struct zhuan{
- int jiazhi;
- int zhongliang;
- bool operator<(const zhuan&rhd)const {
- return jiazhi+zhongliang<rhd.jiazhi+rhd.zhongliang;
- }
- };
- zhuan zhuant[1005];
- int f[1010][50005];
- int main() {
- cin>>n;
- for(int i=1;i<=n;i++){
- cin>>zhuant[i].zhongliang>>zhuant[i].jiazhi;
- w+=zhuant[i].zhongliang;
- }
- sort(zhuant+1,zhuant+n+1);
- for(int i=1;i<=n;i++){
- for(int j=0;j<=w;j++){
- f[i][j]=f[i-1][j]; //不选
- if(j>=zhuant[i].zhongliang && j-zhuant[i].zhongliang<=zhuant[i].jiazhi)
- {
- f[i][j]=max(f[i][j],f[i-1][j-zhuant[i].zhongliang]+zhuant[i].jiazhi);
-
- }
- ans=max(ans,f[i][j]);
- }
- }
- cout<<ans;
- return 0;
- }




