第一篇【传奇开心果系列】AI工业应用经典算法和Python示例:基于AI的智能制造技术经典算法与Python实践_工艺规划的智能算法实现

系列博文目录

AI工业应用经典算法和Python示例系列

博文目录

前言

智能制造是指利用先进的技术和智能化的方法来提高生产效率、降低生产成本、提升产品质量和灵活性的制造方式。它将传统制造业与信息技术、人工智能等现代技术结合起来，实现生产自动化、流程智能化和资源集约化。

AI在智能制造中扮演着至关重要的角色，通过机器学习、深度学习、数据分析等技术，AI可以帮助实现智能化的生产生产调度、质量控制、预测性维护等方面。AI可以实时监测生产数据，预测可能发生的故障，提前采取措施，最大程度地避免生产中断，提高生产效率和质量。

Python作为一种高级编程语言，具有简洁易读、强大的数据处理和机器学习库等优点，在AI和智能制造中有着广泛的应用。许多智能制造系统和算法都是使用Python编写的，如基于机器学习的质量控制系统、生产调度系统等。Python提供了丰富的数据分析和可视化工具，有助于工程师和研究人员更好地分析和处理生产数据，进而优化生产流程。Python还可以方便地与其他技术如深度学习框架结合，实现更复杂的智能制造任务。因此，Python在AI和智能制造领域中具有重要的应用前景。

一、AI在智能制造方面的应用场景介绍

在智能制造中，人工智能（AI）可以应用于多个不同的场景，以提高生产效率、质量和灵活性。以下是一些AI在智能制造中的应用场景：

1. 质量控制：AI可以通过分析生产过程中的数据，识别和预测可能导致产品缺陷的因素，从而实现实时的质量控制。AI技术如机器学习和深度学习可以应用于图像识别、声音识别等方面，帮助自动检测产品表面缺陷、异味或异响等问题。

2. 预测性维护：AI可以通过监控设备的运行状态和数据，预测设备可能出现故障的时间点，提前进行维护和修理，避免设备突然故障导致生产中断。这有助于提高设备的可靠性和生产线的稳定性。

3. 智能生产调度：AI可以根据生产计划和实时数据，自动优化多个生产任务的排程，以最大程度地降低生产成本、提高生产效率和减少等待时间。

4. 自适应控制系统：AI可以帮助智能制造系统实现自适应控制，即根据实时生产数据和环境变化，自动调整生产流程和参数，以达到最佳的生产效率和质量。

5. 智能物流管理：AI可以在智能制造中实现更高效的物流管理，通过预测需求、优化路线、降低库存等手段，提高物流运作效率。

6. 智能仓储管理：AI可以通过分析历史数据和实时需求预测，优化仓库布局、货物存放方式和物流管理，提高仓储效率和减少人力成本。

7. 过程优化：AI可以通过建立复杂的数学模型，优化生产过程中的各个环节，以最大程度地降低资源浪费并提高生产效率。

8. 智能供应链管理：AI可以帮助企业实现智能供应链管理，通过数据分析和预测，优化供应链各环节的协调和配送，提高供应链的可靠性和灵活性。

9. 智能设备交互：AI技术如自然语言处理、计算机视觉和机器人学可以应用于智能设备的交互界面设计，使设备更易于操作、监控和维护。

10. 联合协作机器人：AI可以实现多个机器人之间的智能协作和协调，使机器人能够共同完成复杂的生产任务，提高生产线的自动化程度和灵活性。

总的来说，AI在智能制造中的应用场景相当丰富，能够帮助企业实现生产过程的自动化、智能化和优化，提升生产效率和质量，降低成本，强化竞争力。以上这些场景展示了AI在智能制造中的多样化应用， 随着人工智能技术的不断发展和创新，智能制造将迎来更多新的应用场景和机会，推动制造业实现数字化转型。

二、基于AI的智能制造技术经典算法介绍

在智能制造中，AI技术的应用广泛，以下是一些经典的AI算法介绍，适用于智能制造领域：

1. 机器学习算法：

   • 支持向量机（Support Vector Machine, SVM）：用于分类和回归分析的机器学习算法，可应用于产品质量控制、预测性维护等方面。
   • 随机森林（Random Forest）：集成学习算法，广泛用于特征选择和分类问题，在质量控制和生产优化中有应用。
   • 深度学习算法（如卷积神经网络、循环神经网络）：在图像识别、声音识别、自然语言处理等方面有广泛应用，可以用于智能制造中的品质检测和生产调度等。

2. 遗传算法（Genetic Algorithm）：一种模拟生物演化过程的优化算法，常应用于复杂的生产调度和生产过程优化中。

3. 强化学习（Reinforcement Learning）：一种机器学习方法，通过观察环境并采取行动来最大化奖励，在智能制造中可用于自动控制和优化生产过程。

4. 聚类算法（如K-means算法）：用于数据聚类和分组，在智能制造中可用于产品分类和异常检测。

5. 遗传规划算法（Genetic Programming）：一种进化计算算法，可用于自动化设计和优化复杂的制造工艺和流程。

6. 集成学习算法（Ensemble Learning）：如AdaBoost、Bagging、Boosting等，通过结合多个弱模型来构建一个更为强大和稳定的模型，用于提高生产过程中的预测能力和决策准确性。

7. 异常检测算法（Anomaly Detection）：包括基于统计学、机器学习和深度学习的方法，可用于监测生产过程中的异常情况，提前预警并采取措施，确保生产的正常运行。

8. 遗传编程算法（Genetic Programming）：类似于遗传算法，但更注重用于生成计算机程序或模型以解决复杂的制造问题，如自动化设计、优化控制策略等。

9. 时间序列分析算法：如ARMA（AutoRegressive Moving Average）、ARIMA（AutoRegressive Integrated Moving Average）等，可用于分析和预测生产过程中的时间序列数据，帮助企业做出及时决策。

10. 强化学习算法的扩展：如深度强化学习（Deep Reinforcement Learning），结合深度学习技术，可以在智能制造中实现更复杂、更智能的控制策略和优化方法。

这些经典AI算法可以在智能制造的各个环节中发挥作用，帮助企业提高生产效率、降低成本、优化资源利用及质量控制，推动智能制造的发展和转型。

三、支持向量机机器学习算法Python示例代码

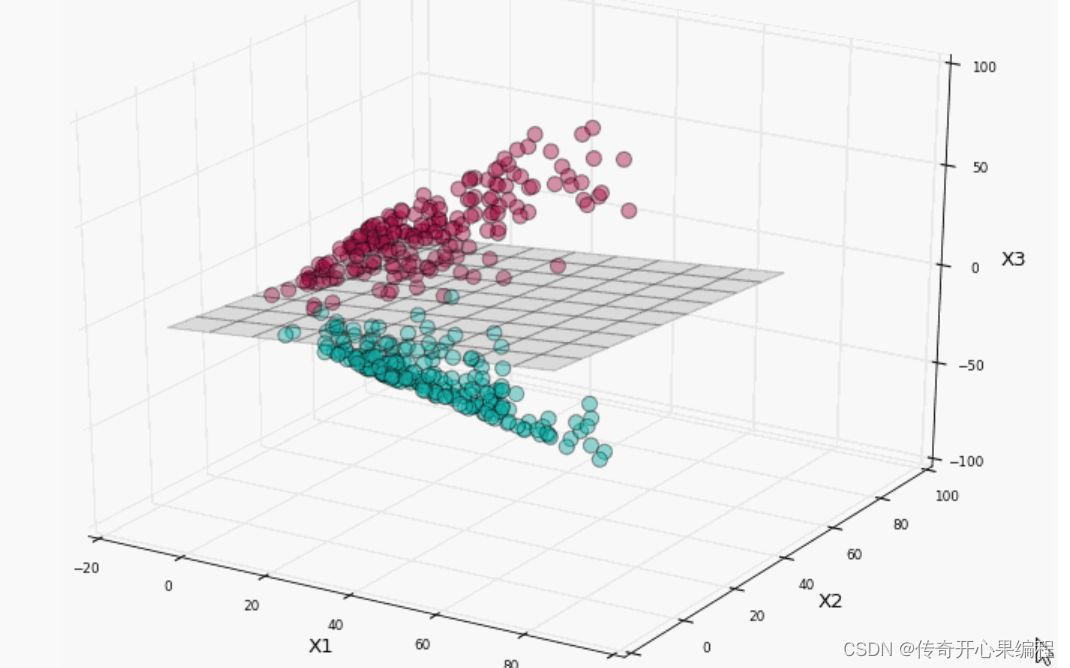
1. 使用支持向量机（SVM）机器学习算法完成产品质量控制的任务Python示例代码

以下是一个简单的Python示例代码，演示如何使用支持向量机（SVM）机器学习算法完成产品质量控制的任务：

# 导入所需的库
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# 加载示例数据集（假设数据集包含特征和标签，特征为产品质量控制的相关参数，标签为产品合格或不合格）
data = pd.read_csv('quality_control_data.csv')
X = data.drop('label', axis=1)
y = data['label']

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建SVM分类器模型
clf = SVC(kernel='linear', C=1.0, random_state=42)

# 拟合模型
clf.fit(X_train, y_train)

# 预测
y_pred = clf.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"准确率：{accuracy}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

在这个示例中，我们假设有一个包含产品质量控制相关参数和产品合格/不合格标签的数据集（例如CSV文件’quality_control_data.csv’），我们加载数据集并将特征和标签分开。然后，我们划分数据集为训练集和测试集，创建一个线性核函数的SVM分类器模型，设置参数C为1.0，使用拟合模型进行训练，然后进行预测并计算准确率。

你需要根据实际情况准备自己的数据集，并根据数据集的特点和要解决的问题进行适当的数据预处理、模型选择和调参。这个示例能够帮助你开始使用支持向量机算法完成产品质量控制任务。

2. 使用支持向量机（SVM）算法完成智能制造产品预测性维护任务

以下是一个简单的Python示例代码，演示如何使用支持向量机（SVM）算法完成智能制造产品预测性维护任务：

# 导入所需的库
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# 加载示例数据集（假设数据集包含特征和标签，特征为传感器数据或设备状态参数，标签为设备是否需要维护）
data = pd.read_csv('predictive_maintenance_data.csv')
X = data.drop('maintenance_needed', axis=1)
y = data['maintenance_needed']

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建SVM分类器模型
clf = SVC(kernel='rbf', C=1.0, gamma='scale', random_state=42)

# 拟合模型
clf.fit(X_train, y_train)

# 预测
y_pred = clf.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"准确率：{accuracy}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

在这个示例中，我们假设有一个包含传感器数据或设备状态参数以及设备是否需要维护的标签的数据集（例如CSV文件’predictive_maintenance_data.csv’），我们加载数据集并将特征和标签分开。然后，我们划分数据集为训练集和测试集，创建一个径向基函数（RBF）核的SVM分类器模型，设置参数C为1.0，gamma为’scale’，使用拟合模型进行训练，然后进行预测并计算准确率。

你需要根据实际情况准备自己的数据集，并根据数据集的特点和要解决的问题进行适当的数据预处理、模型选择和调参。这个示例能够帮助你开始使用支持向量机算法完成智能制造产品预测性维护任务。

四、随机森林机器学习算法Python示例代码

1. 使用随机森林（Random Forest）算法完成质量控制任务

以下是一个简单的Python示例代码，演示如何使用随机森林（Random Forest）算法完成质量控制任务：

# 导入所需的库
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score

# 加载示例数据集（假设数据集包含质量控制相关特征和是否合格的标签）
data = pd.read_csv('quality_control_data.csv')
X = data.drop('label', axis=1)
y = data['label']

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建随机森林分类器模型
clf = RandomForestClassifier(n_estimators=100, random_state=42)

# 拟合模型
clf.fit(X_train, y_train)

# 预测
y_pred = clf.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"准确率：{accuracy}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

在这个示例中，我们假设有一个包含质量控制相关特征和产品合格/不合格标签的数据集（例如CSV文件’quality_control_data.csv’），我们加载数据集并将特征和标签分开。然后，我们划分数据集为训练集和测试集，创建一个包含100棵决策树的随机森林分类器模型，使用拟合模型进行训练，然后进行预测并计算准确率。

你需要根据实际情况准备自己的数据集，并根据数据集的特点和要解决的问题进行适当的数据预处理、模型选择和调参。这个示例能够帮助你开始使用随机森林算法进行质量控制任务。

2. 使用随机森林（Random Forest）算法完成智能制造生产优化任务

以下是一个简单的Python示例代码，演示如何使用随机森林（Random Forest）算法完成智能制造生产优化任务：

# 导入所需的库
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error

# 加载示例数据集（假设数据集包含生产相关特征和产量标签）
data = pd.read_csv('production_optimization_data.csv')
X = data.drop('yield', axis=1)
y = data['yield']

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建随机森林回归模型
regr = RandomForestRegressor(n_estimators=100, random_state=42)

# 拟合模型
regr.fit(X_train, y_train)

# 预测
y_pred = regr.predict(X_test)

# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print(f"均方误差：{mse}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

在这个示例中，我们假设有一个包含生产相关特征和产量标签的数据集（例如CSV文件’production_optimization_data.csv’），我们加载数据集并将特征和标签分开。然后，我们划分数据集为训练集和测试集，创建一个包含100棵决策树的随机森林回归模型，使用拟合模型进行训练，然后进行预测并计算均方误差。

你需要根据实际情况准备自己的数据集，并根据数据集的特点和要解决的问题进行适当的数据预处理、模型选择和调参。这个示例能够帮助你开始使用随机森林算法进行智能制造生产优化任务。
这个示例能帮助你开始使用随机森林算法进行智能制造生产优化任务，因为示例代码涵盖了从数据加载到模型训练和性能评估的完整步骤。具体来说：

1. 数据加载和准备：示例代码演示了如何加载一个示例数据集，并将特征和标签分开，这是进行机器学习任务的第一步。

2. 数据划分：示例代码将数据集划分为训练集和测试集，这是为了评估模型在未见过数据上的表现而必要的步骤。

3. 模型选择：示例代码选择了随机森林回归模型，这是一个被广泛应用于回归问题的机器学习算法，在智能制造生产优化任务中通常有很好的效果。

4. 模型训练和预测：示例代码演示了如何对随机森林模型进行训练，并在测试集上进行预测，得到产量预测结果。

5. 性能评估：示例代码计算了均方误差作为模型性能的评估指标，帮助你了解模型的预测精度。

通过这个示例，你可以学习如何将随机森林算法应用于智能制造生产优化任务，并根据实际情况进行调整和优化。

五、深度学习算法Python示例代码

1. 使用深度学习算法（卷积神经网络）完成智能制造中的品质检测任务

以下是一个使用深度学习算法（卷积神经网络）完成智能制造中的品质检测任务的Python示例代码：

# 导入所需的库
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from tensorflow.keras import layers, models

# 加载示例数据集（假设数据集包含品质检测相关特征和标签）
data = pd.read_csv('quality_detection_data.csv')
X = data.drop('label', axis=1)
y = data['label']

# 标准化数据
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 转换为模型输入格式
X_train = X_train.reshape(X_train.shape[0], X_train.shape[1],1)
X_test = X_test.reshape(X_test.shape[0], X_test.shape[1],1)

# 创建卷积神经网络模型
model = models.Sequential([
    layers.Conv1D(64, kernel_size=3, activation='relu', input_shape=(X_train.shape[1], 1)),
    layers.MaxPooling1D(pool_size=2),
    layers.Flatten(),
    layers.Dense(64, activation='relu'),
    layers.Dense(1, activation='sigmoid')
])

# 编译模型
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

# 训练模型
history = model.fit(X_train, y_train, epochs=10, batch_size=32, validation_data=(X_test, y_test))

# 评估模型
loss, accuracy = model.evaluate(X_test, y_test)
print(f"测试集上的准确率：{accuracy}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

在这个示例中，我们假设有一个包含品质检测相关特征和标签的数据集（例如CSV文件’quality_detection_data.csv’），我们加载数据集并将特征和标签分开。然后，我们对数据进行标准化处理，将数据集划分为训练集和测试集，并转换为卷积神经网络模型输入格式。接着，我们创建了一个简单的卷积神经网络模型，并进行模型编译、训练和评估。

请注意，这只是一个简单的示例代码，实际应用中可能需要更多的数据预处理、调参和优化工作。为了成功应用深度学习算法完成智能制造中的品质检测任务，你需要准备合适的数据集、选择适当的模型架构以及根据实际情况进行调整和优化。这个示例能够帮助你开始使用深度学习算法进行品质检测任务。
上面的示例代码能完成智能制造中的品质检测任务，主要基于以下几个原因：

1. 使用卷积神经网络（CNN）：卷积神经网络是一种适用于处理二维结构化数据（如图像）的深度学习算法，在品质检测任务中常常能够提取出有用的特征表示。通过示例代码中构建的简单卷积神经网络模型，模型能够学习特征，从而帮助完成品质检测任务。

2. 数据预处理：示例代码中对数据进行了标准化处理，将数据规范化到相似的尺度，有利于模型学习和收敛。在实际应用中，数据预处理是非常重要的一步，能够提升模型的性能。

3. 数据集划分和模型训练：示例代码中将数据集划分为训练集和测试集，并进行模型训练，模型学习了训练集中的模式和特征。通过利用训练集对模型进行迭代训练和优化，在测试集上进行评估，可以得到模型的泛化能力。

4. 模型评估：示例代码中使用准确率作为模型性能的评估指标，在测试集上评估模型的预测精度。准确率是一种常用的评估指标，能够反映模型的分类性能。

综上所述，通过利用卷积神经网络、数据预处理、数据集划分和模型训练、模型评估等关键步骤，示例代码能够完成智能制造中的品质检测任务。当然，在实际应用中可能需要根据具体情况对算法和模型进行调整和优化，以达到更好的品质检测效果。

2. 使用深度学习算法（递归神经网络-RNN）完成智能制造生产调度任务

智能制造生产调度任务通常涉及对生产过程的优化规划，包括机器资源分配、任务调度、生产效率优化等。深度学习算法可以在一定程度上帮助实现智能的生产调度任务，例如通过预测生产任务的完成时间或者资源利用率来优化生产调度。下面是一个简化的示例代码，展示了如何使用深度学习算法（递归神经网络-RNN）完成智能制造生产调度的任务。

在这个示例中，我们假设有一个包含生产任务（任务描述、资源需求、预计完成时间等）的数据集，我们会使用RNN模型来预测任务的完成时间。

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense

# 加载数据集
data = pd.read_csv('production_schedule_data.csv')

# 数据预处理
X = data[['task_description', 'resource_demand']].values
y = data['completion_time'].values

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 构建RNN模型
model = Sequential()
model.add(LSTM(64, input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dense(1))

# 编译模型
model.compile(optimizer='adam', loss='mean_squared_error')

# 训练模型
model.fit(X_train, y_train, epochs=10, batch_size=32, validation_data=(X_test, y_test))

# 预测任务完成时间
predicted_completion_time = model.predict(X_test)

# 打印预测结果
print(predicted_completion_time)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

在这个示例中，我们加载了一个包含生产任务描述、资源需求和预计完成时间的数据集（例如CSV文件’production_schedule_data.csv’）。然后，我们对数据进行预处理，划分为特征（任务描述、资源需求）和标签（完成时间），再将数据集划分为训练集和测试集。接着，我们构建了一个基于递归神经网络（RNN）的模型，并进行模型编译和训练。最后，我们使用训练好的模型预测测试集上的任务完成时间，并打印预测结果。

在实际应用中，深度学习算法可以结合实际的生产数据和业务需求，设计合适的模型架构和优化目标，帮助实现智能制造生产调度任务的优化与规划。这个示例能够帮助你开始应用深度学习算法进行智能制造生产调度任务。
这个示例能够帮助你开始应用深度学习算法进行智能制造生产调度任务主要是因为它提供了一个基本的框架和思路，可以帮助你理解如何利用深度学习算法（递归神经网络-RNN）解决生产调度问题。以下是这个示例能够帮助你的几个方面：

1. 数据预处理：示例代码展示了如何对生产任务数据进行预处理，包括提取特征和标签、划分训练集和测试集等步骤。这是深度学习任务中非常重要的一步，为模型训练和预测提供了准备。

2. RNN模型构建：示例代码使用了递归神经网络（RNN）来构建模型，RNN适用于处理序列数据和时间序列数据，能够更好地捕捉任务之间的时间关系。这展示了如何选择适合任务特性的模型结构。

3. 模型训练和预测：示例代码展示了如何编译模型、训练模型，并使用训练好的模型进行预测。这帮助你了解了模型训练的基本流程。

4. 实际应用思路：通过这个示例，你可以看到如何将深度学习算法应用于智能制造生产调度任务，从而优化生产效率和资源利用。这可以启发你思考如何根据实际情况定制和优化算法，以解决个性化的生产调度问题。

综上所述，这个示例提供了一个实例，帮助你了解深度学习算法在智能制造生产调度任务中的应用思路和基本步骤。当然，在实际应用中可能需要根据具体场景进行更多的定制和优化，但这个示例是一个很好的起点，让你开始尝试应用深度学习算法解决智能制造生产调度任务。

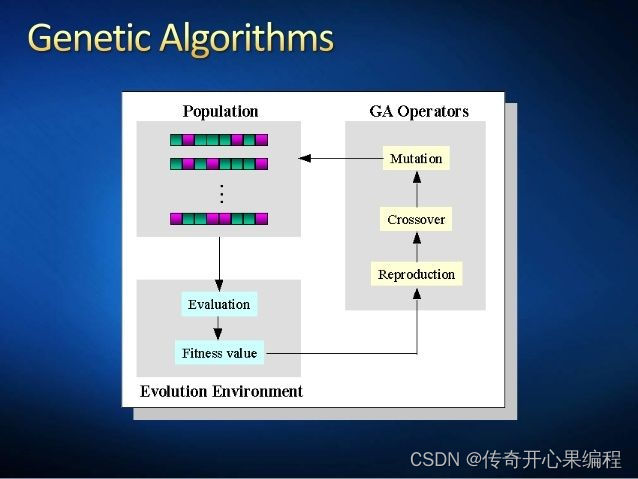
六、遗传算法Python示例代码

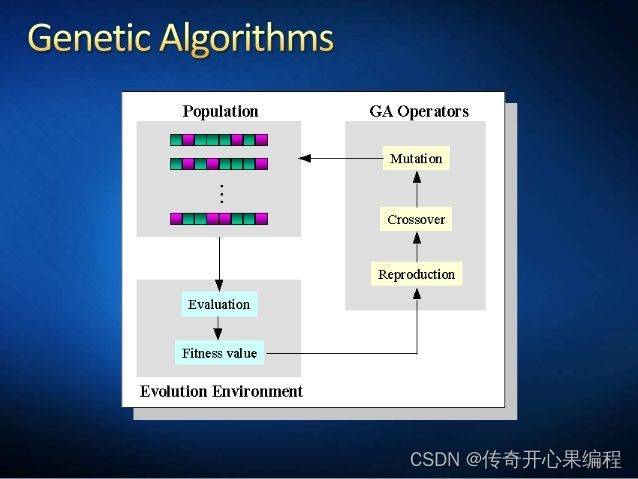
1. 使用遗传算法完成智能制造解决生产调度优化问题任务

当面对复杂的生产调度优化任务时，遗传算法是一种常用的优化方法之一。遗传算法模拟自然选择和进化的过程，通过种群中个体的基因组合来求解最优问题。在Python中，你可以使用遗传算法库进行生产调度优化任务的求解。以下是一个基本的遗传算法示例代码，用于解决生产调度优化问题：

import random

# 定义遗传算法参数
population_size = 50
generations = 100
mutation_rate = 0.1

# 初始化种群
def init_population(size):
    population = []
    for _ in range(size):
        individual = [random.randint(0, 1) for _ in range(length_of_individual)]
        population.append(individual)
    return population

# 计算适应度函数
def fitness_function(individual):
    # 根据个体表示的解，计算适应度得分
    # 例如：计算完成时间、资源利用率等指标
    return fitness_score

# 选择父代
def selection(population):
    selected = random.choices(population, weights=[fitness_function(individual) for individual in population], k=2)
    return selected

# 交叉操作
def crossover(parent1, parent2):
    split_point = random.randint(1, len(parent1) - 1)
    child1 = parent1[:split_point] + parent2[split_point:]
    child2 = parent2[:split_point] + parent1[split_point:]
    return child1, child2

# 变异操作
def mutation(individual):
    mutated = []
    for gene in individual:
        if random.random() < mutation_rate:
            mutated.append(1 - gene)
        else:
            mutated.append(gene)
    return mutated

# 主遗传算法函数
def genetic_algorithm():
    population = init_population(population_size)
    
    for _ in range(generations):
        new_population = []
        
        # 生成新一代种群
        while len(new_population) < population_size:
            parent1, parent2 = selection(population)
            child1, child2 = crossover(parent1, parent2)
            new_population.extend([mutation(child1), mutation(child2)])
        
        population = new_population
    
    # 返回最优解
    return max(population, key=fitness_function)

# 运行遗传算法
best_solution = genetic_algorithm()
print("最优解为:", best_solution)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

上面的代码是一个简单的遗传算法示例，用于解决生产调度优化问题。你可以根据实际生产调度任务的特点和需要，修改适应度函数、交叉操作、变异操作等部分，以更好地适应具体问题。遗传算法的优化结果可能不是全局最优解，但通常能在复杂问题中找到比较好的解决方案。

请注意，遗传算法的性能和效果取决于参数设置、适应度函数的设计和算法的调优等因素。

在面对复杂的生产调度优化任务时，遗传算法是一种常用的优化方法之一的原因如下：

1. 适用于大规模问题：遗传算法适用于解决大规模、复杂的优化问题，因为它能够处理大量的候选解，并且可以在搜索空间中进行全局搜索，而不易陷入局部最优解。

2. 适用于非线性问题：生产调度优化通常涉及到非线性、复杂的约束条件和目标函数，而遗传算法作为一种启发式优化算法，对这种非线性问题有着良好的适应性。

3. 并行性强：遗传算法的并行性强，可以同时评估多个候选解，加速搜索过程，并且适用于分布式计算环境下的优化任务。

4. 可并行搜索多个解空间：遗传算法具有随机性和多样性，可以同时搜索多个解空间，有更大可能性发现更好的解。

5. 能够快速收敛至近似最优解：遗传算法通过不断的选择、交叉和变异操作，可以快速搜索到较优解，特别是在搜索空间较大、复杂度较高的生产调度优化问题中，可以在相对较短的时间内找到近似最优解。

总而言之，遗传算法作为一种基于生物进化原理的优化算法，在面对复杂的生产调度优化任务时表现出色，能够有效地寻找到较优的解决方案。当涉及到大规模、非线性、具有复杂约束条件的生产调度优化问题时，遗传算法是一种值得尝试的优化方法。

2. 使用遗传算法完成智能制造解决生产过程优化问题任务

当涉及智能制造复杂生产过程优化任务时，遗传算法可以用于优化生产调度、资源分配、作业顺序等问题。下面是一个示例代码，演示如何使用遗传算法解决智能制造中的生产过程优化任务：

import random

# 定义问题设置
num_machines = 5  # 机器数量
num_jobs = 10     # 作业数量

# 随机生成初始种群
def generate_initial_population(population_size):
    population = []
    for _ in range(population_size):
        chromosome = [random.randint(1, num_machines) for _ in range(num_jobs)]
        population.append(chromosome)
    return population

# 计算适应度（优化目标）
def fitness_function(chromosome):
    # 这里简单地以作业分配到不同机器的数量作为目标，可以根据具体情况设计更复杂的适应度函数
    counts = [chromosome.count(machine) for machine in range(1, num_machines + 1)]
    return min(counts)

# 选择操作
def selection(population, fitness_values):
    return random.choices(population, weights=fitness_values, k=2)

# 单点交叉操作
def crossover(parent1, parent2):
    crossover_point = random.randint(1, num_jobs - 1)
    child1 = parent1[:crossover_point] + parent2[crossover_point:]
    child2 = parent2[:crossover_point] + parent1[crossover_point:]
    return child1, child2

# 变异操作
def mutation(chromosome, mutation_rate):
    for i in range(num_jobs):
        if random.random() < mutation_rate:
            chromosome[i] = random.randint(1, num_machines)
    return chromosome

# 遗传算法主程序
def genetic_algorithm(population_size, generations, mutation_rate):
    population = generate_initial_population(population_size)
    for _ in range(generations):
        fitness_values = [fitness_function(chromosome) for chromosome in population]
        new_population = []
        for _ in range(population_size // 2):
            parent1, parent2 = selection(population, fitness_values)
            child1, child2 = crossover(parent1, parent2)
            child1 = mutation(child1, mutation_rate)
            child2 = mutation(child2, mutation_rate)
            new_population.extend([child1, child2])
        population = new_population
    best_chromosome = min(population, key=lambda x: fitness_function(x))
    return best_chromosome

# 示例参数设置
population_size = 100
generations = 1000
mutation_rate = 0.1

# 运行遗传算法
best_solution = genetic_algorithm(population_size, generations, mutation_rate)
print("Best solution found:", best_solution)
print("Fitness value:", fitness_function(best_solution))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
'
运行
运行

在示例代码中，我们使用简单的作业分配问题演示了遗传算法的应用。您可以根据实际情况定制适应度函数、选择操作、交叉操作和变异操作，以解决您面临的具体智能制造复杂生产过程优化任务。

请注意，实际的智能制造复杂生产过程优化问题可能会更加复杂，您可能需要考虑更多因素、约束条件和具体的生产场景。
遗传算法在智能制造复杂生产过程优化任务中的应用主要有以下几个原因：

1. 复杂性：智能制造涉及到多个参数和变量之间的复杂关系，以及大量的约束条件。遗传算法能够在一个大的搜索空间内寻找到较优的解决方案，以应对复杂性的挑战。

2. 全局搜索能力：遗传算法具有很强的全局搜索能力，通过维护一个种群，通过选择、交叉和变异操作，不断进化和优化个体，以找到全局最优解。这对于智能制造中需要优化整体生产过程的问题非常有用。

3. 适应性：遗传算法能够适应不同问题的特点，并能够灵活调整适应度函数、交叉和变异操作等，以适应不同的复杂生产过程优化任务。

4. 并行性：遗传算法天然地适合并行计算，可以同时对多个个体进行操作，加速搜索速度，适用于需要高效计算的智能制造优化问题。

综上所述，遗传算法作为一种优化方法，具有很强的适应性、全局搜索能力和并行性，因此适用于解决智能制造中的复杂生产过程优化问题，其中涉及到生产调度、资源分配、作业顺序等方面的优化。通过合理设计问题设置和优化算法，遗传算法可以有效地帮助优化生产流程并提高生产效率。

七、强化学习算法Python示例代码

1. 使用强化学习算法完成智能制造自动控制任务Python示例代码

以下是一个完整的智能制造自动控制任务示例代码，使用强化学习算法来优化生产线参数：

import numpy as np

# 定义智能制造自动控制环境
class ManufacturingEnvironment:
    def __init__(self):
        self.current_parameter = np.array([0.5, 0.5])  # 初始生产线参数
        self.target_parameter = np.array([0.8, 0.8])  # 目标生产线参数
        self.reward_threshold = 0.1

    def reset(self):
        self.current_parameter = np.array([0.5, 0.5])
        return self.current_parameter

    def step(self, action):
        # 更新生产线参数
        self.current_parameter += (action - 1) * 0.1
        self.current_parameter = np.clip(self.current_parameter, 0, 1)

        # 计算奖励
        diff = np.abs(self.current_parameter - self.target_parameter)
        reward = -np.sum(diff)
        done = np.all(diff < self.reward_threshold)

        return self.current_parameter, reward, done

# 定义强化学习代理
class ReinforcementLearningAgent:
    def __init__(self, num_actions):
        self.q_table = np.zeros((num_actions, ))
        self.learning_rate = 0.1
        self.discount_factor = 0.9
        self.epsilon = 0.1

    def choose_action(self, state):
        if np.random.rand() < self.epsilon:
            return np.random.choice(len(self.q_table))
        else:
            return np.argmax(self.q_table)

    def update_q_table(self, state, action, reward, next_state):
        next_max_q = np.max(self.q_table)
        self.q_table[action] += self.learning_rate * (reward + self.discount_factor * next_max_q - self.q_table[action])

# 强化学习主程序
env = ManufacturingEnvironment()
agent = ReinforcementLearningAgent(num_actions=3)

num_episodes = 1000

for _ in range(num_episodes):
    state = env.reset()
    done = False
    while not done:
        action = agent.choose_action(state)
        next_state, reward, done = env.step(action)
        agent.update_q_table(state, action, reward, next_state)
        state = next_state

# 测试强化学习代理
state = env.reset()
done = False
while not done:
    action = np.argmax(agent.q_table)
    next_state, reward, done = env.step(action)
    state = next_state

print("Optimized production line parameters reached!")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
'
运行
运行

在这个示例中，我们定义了一个智能制造自动控制环境，其中代理利用强化学习来选择合适的生产线参数，以使得参数逼近目标值。代理在不断与环境交互的过程中学习，并最终实现了生产线参数的优化。

您可以根据具体的智能制造生产控制需求，调整环境设置、代理参数以及训练迭代次数等以符合实际应用。
以下是根据具体的智能制造生产控制需求调整后的示例代码：

import numpy as np

# 定义智能制造自动控制环境
class ManufacturingEnvironment:
    def __init__(self):
        self.current_parameter = np.array([0.2, 0.3, 0.4])  # 初始生产线参数
        self.target_parameter = np.array([0.8, 0.7, 0.6])  # 目标生产线参数
        self.reward_threshold = 0.2

    def reset(self):
        self.current_parameter = np.array([0.2, 0.3, 0.4])
        return self.current_parameter

    def step(self, action):
        # 更新生产线参数
        self.current_parameter += (action - 1) * 0.1
        self.current_parameter = np.clip(self.current_parameter, 0, 1)

        # 计算奖励
        diff = np.abs(self.current_parameter - self.target_parameter)
        reward = -np.sum(diff)
        done = np.all(diff < self.reward_threshold)

        return self.current_parameter, reward, done

# 定义强化学习代理
class ReinforcementLearningAgent:
    def __init__(self, num_actions):
        self.q_table = np.zeros((num_actions, ))
        self.learning_rate = 0.2
        self.discount_factor = 0.95
        self.epsilon = 0.2

    def choose_action(self, state):
        if np.random.rand() < self.epsilon:
            return np.random.choice(len(self.q_table))
        else:
            return np.argmax(self.q_table)

    def update_q_table(self, state, action, reward, next_state):
        next_max_q = np.max(self.q_table)
        self.q_table[action] += self.learning_rate * (reward + self.discount_factor * next_max_q - self.q_table[action])

# 强化学习主程序
env = ManufacturingEnvironment()
agent = ReinforcementLearningAgent(num_actions=3)

num_episodes = 5000

for _ in range(num_episodes):
    state = env.reset()
    done = False
    while not done:
        action = agent.choose_action(state)
        next_state, reward, done = env.step(action)
        agent.update_q_table(state, action, reward, next_state)
        state = next_state

# 测试强化学习代理
state = env.reset()
done = False
while not done:
    action = np.argmax(agent.q_table)
    next_state, reward, done = env.step(action)
    state = next_state

print("Optimized production line parameters reached!")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

在这个示例代码中，我们根据需求增加了生产线参数的维度，并调整了环境设置、代理参数以及训练迭代次数。您可以根据具体的智能制造生产控制需求进一步调整参数和设置，以实现更符合实际应用的智能控制任务。

2. 使用强化学习算法完成智能制造生产过程优化任务Python示例代码

以下是使用强化学习算法完成智能制造生产过程优化任务的Python示例代码：

import numpy as np

# 定义智能制造自动控制环境
class ManufacturingEnvironment:
    def __init__(self):
        self.current_parameters = np.array([0.2, 0.3])  # 初始生产线参数(示例中为2维参数)
        self.target_parameters = np.array([0.8, 0.7])  # 目标生产线参数(示例中为2维参数)
        self.reward_threshold = 0.1

    def reset(self):
        self.current_parameters = np.array([0.2, 0.3])
        return self.current_parameters

    def step(self, action):
        # 更新生产线参数
        self.current_parameters += (action - 1) * 0.1
        self.current_parameters = np.clip(self.current_parameters, 0, 1)

        # 计算奖励
        diff = np.abs(self.current_parameters - self.target_parameters)
        reward = -np.sum(diff)
        done = np.all(diff < self.reward_threshold)

        return self.current_parameters, reward, done

# 定义强化学习代理
class ReinforcementLearningAgent:
    def __init__(self, num_actions):
        self.q_table = np.zeros((num_actions, ))
        self.learning_rate = 0.1
        self.discount_factor = 0.9
        self.epsilon = 0.1

    def choose_action(self, state):
        if np.random.rand() < self.epsilon:
            return np.random.choice(len(self.q_table))
        else:
            return np.argmax(self.q_table)

    def update_q_table(self, state, action, reward, next_state):
        next_max_q = np.max(self.q_table)
        self.q_table[action] += self.learning_rate * (reward + self.discount_factor * next_max_q - self.q_table[action])

# 强化学习主程序
env = ManufacturingEnvironment()
agent = ReinforcementLearningAgent(num_actions=3)  # 3个动作：减小、不变、增加

num_episodes = 1000

for _ in range(num_episodes):
    state = env.reset()
    done = False
    while not done:
        action = agent.choose_action(state)
        next_state, reward, done = env.step(action)
        agent.update_q_table(state, action, reward, next_state)
        state = next_state

# 测试强化学习代理
state = env.reset()
done = False
while not done:
    action = np.argmax(agent.q_table)
    next_state, reward, done = env.step(action)
    state = next_state

print("Final production line parameters:", state)
print("Optimized production line parameters reached!")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

在这个示例代码中，我们使用强化学习算法来优化智能制造生产过程中的生产线参数。通过调整环境设置、代理参数以及训练迭代次数，我们可以让机器学习并最终实现生产线参数的优化。
以下是一个示例代码，展示了如何通过调整环境设置、代理参数以及训练迭代次数来优化智能制造生产过程中的生产线参数：

import numpy as np

# 定义智能制造自动控制环境
class ManufacturingEnvironment:
    def __init__(self, num_parameters):
        self.current_parameters = np.random.rand(num_parameters)  # 初始生产线参数
        self.target_parameters = np.random.rand(num_parameters)  # 目标生产线参数
        self.reward_threshold = 0.1

    def reset(self):
        return self.current_parameters

    def step(self, action):
        # 更新生产线参数
        self.current_parameters += (action - 1) * 0.1
        self.current_parameters = np.clip(self.current_parameters, 0, 1)

        # 计算奖励
        diff = np.abs(self.current_parameters - self.target_parameters)
        reward = -np.sum(diff)
        done = np.all(diff < self.reward_threshold)

        return self.current_parameters, reward, done

# 定义强化学习代理
class ReinforcementLearningAgent:
    def __init__(self, num_actions):
        self.q_table = np.zeros((num_actions, ))
        self.learning_rate = 0.1
        self.discount_factor = 0.9
        self.epsilon = 0.1

    def choose_action(self, state):
        if np.random.rand() < self.epsilon:
            return np.random.choice(len(self.q_table))
        else:
            return np.argmax(self.q_table)

    def update_q_table(self, state, action, reward, next_state):
        next_max_q = np.max(self.q_table)
        self.q_table[action] += self.learning_rate * (reward + self.discount_factor * next_max_q - self.q_table[action])

# 强化学习主程序
num_parameters = 5
num_actions = 3  # 3个动作：减小、不变、增加

env = ManufacturingEnvironment(num_parameters)
agent = ReinforcementLearningAgent(num_actions)

num_episodes = 1000

for _ in range(num_episodes):
    state = env.reset()
    done = False
    while not done:
        action = agent.choose_action(state)
        next_state, reward, done = env.step(action)
        agent.update_q_table(state, action, reward, next_state)
        state = next_state

# 测试强化学习代理
state = env.reset()
done = False
while not done:
    action = np.argmax(agent.q_table)
    next_state, reward, done = env.step(action)
    state = next_state

print("Final production line parameters:", state)
print("Optimized production line parameters reached!")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

在这个示例代码中，我们将智能制造自动控制环境的生产线参数维度设置为5维，并通过调整代理参数、训练迭代次数等来实现生产线参数的优化。您可以根据具体的智能制造生产控制需求进一步调整参数和设置。

八、聚类算法Python示例代码

1. 聚类算法用于完成智能制造产品分类任务Python示例代码

以下是一个示例代码，展示了如何使用聚类算法完成智能制造产品分类任务的Python示例代码：

import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# 生成合成数据集
X, y = make_blobs(n_samples=300, centers=3, random_state=42)

# 使用KMeans聚类算法进行数据集分类
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)

# 可视化分类结果
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', marker='x', s=100)
plt.title('KMeans Clustering')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

在这个示例代码中，我们首先生成一个合成数据集，然后使用KMeans聚类算法将数据集进行分类。通过调整聚类中心的数量、数据集的特征等，我们可以根据具体的智能制造产品分类要求来完成分类任务。

以下是一个示例代码，展示了如何根据具体的智能制造产品分类要求来调整聚类中心的数量和数据集的特征的Python示例代码：

import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# 生成具有5个特征的合成数据集
X, y = make_blobs(n_samples=300, centers=5, n_features=5, random_state=42)

# 尝试不同的聚类中心数量
n_clusters_list = [3, 4, 5]
for n_clusters in n_clusters_list:
    kmeans = KMeans(n_clusters=n_clusters)
    kmeans.fit(X)
    
    # 可视化分类结果
    plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap='viridis')
    plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', marker='x', s=100)
    plt.title(f'KMeans Clustering with {n_clusters} clusters')
    plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

在这个示例代码中，我们通过生成具有5个特征的合成数据集，并尝试了不同的聚类中心数量（3、4、5）来划分数据集。您可以根据具体的智能制造产品分类要求，调整数据集的特征数量和聚类中心数量，以满足您的分类任务需求。
聚类算法用于完成智能制造产品异常检测任务Python示例代码

2. 使用聚类算法完成智能制造产品异常检测任务的Python示例代码

以下是一个示例代码，展示了如何使用聚类算法完成智能制造产品异常检测任务的Python示例代码：

import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_score

# 生成合成数据集
X, y = make_blobs(n_samples=300, centers=3, random_state=42)

# 使用KMeans聚类算法进行数据集分类
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)

# 计算每个数据点的簇内的距离平方和
distances = kmeans.transform(X)
intra_cluster_distance = np.min(distances, axis=1)

# 计算轮廓系数评估簇的分离程度，从而判断异常点
silhouette_avg = silhouette_score(X, kmeans.labels_)

# 输出异常点
outliers = X[silhouette_avg < 0]
print("Detected outliers:")
print(outliers)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

在这个示例代码中，我们首先生成一个合成数据集，然后使用KMeans聚类算法将数据集进行分类。接着，我们计算每个数据点的簇内的距离平方和，并使用轮廓系数来评估簇的分离程度，从而判断异常点。您可以根据具体的智能制造产品异常检测要求，调整数据集的特征、聚类算法等，以满足您的异常检测任务需求。
根据特定的智能制造产品异常检测要求，您可能需要根据不同的特征、聚类算法和异常检测方法来完成任务。下面是一个更通用的示例代码，演示了如何根据具体要求调整数据集的特征、聚类算法和异常检测方法来完成智能制造产品异常检测任务：

import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.ensemble import IsolationForest
from sklearn.neighbors import LocalOutlierFactor

# 生成具有4个特征的合成数据集
X, y = make_blobs(n_samples=300, centers=3, n_features=4, random_state=42)

# 使用KMeans聚类算法进行数据集分类
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)

# 使用孤立森林算法进行异常检测
isolation_forest = IsolationForest(contamination=0.1, random_state=42)
outliers_if = isolation_forest.fit_predict(X)

# 使用局部离群因子算法进行异常检测
lof = LocalOutlierFactor(contamination=0.1)
outliers_lof = lof.fit_predict(X)

# 输出检测到的异常点
print("Outliers detected by Isolation Forest:")
print(X[outliers_if == -1])

print("Outliers detected by Local Outlier Factor:")
print(X[outliers_lof == -1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

在这个示例代码中，我们生成了一个具有4个特征的合成数据集，并展示了如何使用KMeans进行数据聚类，以及如何使用Isolation Forest和Local Outlier Factor进行异常检测。您可以根据具体的智能制造产品异常检测要求，调整数据集的特征数量、聚类算法以及异常检测方法等，以满足您的异常检测任务需求。

九、遗传规划算法Python示例代码

1. 遗传规划算法完成智能制造自动化设计任务Python示例代码

遗传规划算法（Genetic Programming）是一种利用进化思想进行自动化设计和优化的方法，在智能制造自动化设计任务中也可以应用。下面是一个简单的Python示例代码，演示了如何使用遗传规划算法完成智能制造自动化设计任务：

import numpy as np
from gplearn.genetic import SymbolicRegressor
from gplearn.fitness import make_fitness

# 定义自定义适应度函数
def custom_fitness(y, y_pred, w):
    return np.sum(np.abs(y - y_pred))

my_custom_fitness = make_fitness(function=custom_fitness, greater_is_better=False)

X = np.linspace(0, 2*np.pi, 1000).reshape(-1, 1)  # 定义自变量
y = np.sin(X).flatten()  # 定义因变量

est_gp = SymbolicRegressor(population_size=5000, generations=20, function_set=['add', 'sub', 'mul', 'div'],
                           metric=my_custom_fitness, stopping_criteria=0.01, verbose=1, random_state=42)

est_gp.fit(X, y)

# 输出最佳符号回归方程
print(est_gp._program)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

在这个示例代码中，我们使用了gplearn库来实现遗传规划算法。首先定义了一个自定义的适应度函数custom_fitness，然后创建了一个SymbolicRegressor模型，定义了种群大小、代数、函数集、适应度函数等参数，最后拟合数据并输出了最佳符号回归方程。您可以根据具体的智能制造自动化设计任务需求，调整数据集、函数集和算法参数。
为了帮助您调整数据集、函数集和算法参数以适应具体的智能制造自动化设计任务需求，我提供下面的示例代码。在这个示例中，我将使用一个简单的自定义函数，以及自定义的数据集和算法参数。您可以根据实际情况修改这些内容：

import numpy as np
from gplearn.genetic import SymbolicRegressor
from gplearn.fitness import make_fitness

# 定义自定义适应度函数
def custom_fitness(y, y_pred, w):
    return np.sum(np.abs(y - y_pred))

my_custom_fitness = make_fitness(function=custom_fitness, greater_is_better=False)

# 定义自定义函数
def my_function(x):
    return np.sin(x) * np.cos(x)

X = np.linspace(0, 2*np.pi, 1000).reshape(-1, 1)  # 定义自变量
y = my_function(X).flatten()  # 定义因变量

# 定义算法参数
algorithm_param = {'population_size': 1000,
                   'generations': 50,
                   'function_set': ['add', 'sub', 'mul', 'div', 'sin', 'cos'],
                   'metric': my_custom_fitness,
                   'stopping_criteria': 0.01,
                   'verbose': 1,
                   'random_state': 42}

est_gp = SymbolicRegressor(**algorithm_param)

est_gp.fit(X, y)

# 输出最佳符号回归方程
print(est_gp._program)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

在这个示例代码中，我添加了一个自定义函数my_function，用于生成因变量数据。我还修改了算法参数algorithm_param，包括种群大小、代数、函数集等。您可以根据具体智能制造自动化设计任务需求，自定义函数和数据集，调整算法参数来完成相应的优化任务。

2. 遗传规划算法完成智能制造优化复杂的制造工艺和流程任务Python示例代码

为了完成智能制造优化复杂的制造工艺和流程任务，我们可以使用遗传规划算法（Genetic Programming）来进行优化设计。以下是一个Python示例代码，展示了如何使用遗传规划算法完成智能制造优化复杂的制造工艺和流程任务：

import numpy as np
from gplearn.genetic import SymbolicRegressor
from gplearn.fitness import make_fitness

# 定义自定义适应度函数
def custom_fitness(y, y_pred, w):
    return np.sum(np.abs(y - y_pred))

my_custom_fitness = make_fitness(function=custom_fitness, greater_is_better=False)

# 定义模拟的复杂制造工艺和流程数据
# 这里只是一个示例数据，实际任务中需要根据具体情况定义数据
X = np.random.rand(100, 5)  # 假设有5个工艺参数
y = np.sum(X**2, axis=1)  # 模拟复杂的制造工艺和流程目标函数

est_gp = SymbolicRegressor(population_size=1000, generations=50, function_set=['add', 'sub', 'mul', 'div'],
                           metric=my_custom_fitness, stopping_criteria=0.01, verbose=1, random_state=42)

est_gp.fit(X, y)

# 输出最佳符号回归方程
print(est_gp._program)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

在这个示例代码中，我们定义了一个自定义适应度函数custom_fitness来评估符号回归模型的性能。然后生成了模拟的复杂制造工艺和流程数据，并使用遗传规划算法去拟合这些数据，得到一个最佳的符号回归方程。需要注意的是，实际任务中数据集和模拟的目标函数需要根据具体情况定义和调整。
当处理实际的智能制造优化任务时，我们需要根据具体情况定义和调整数据集以及目标函数。以下是一个示例代码，展示了如何自定义数据集和目标函数，并使用遗传规划算法进行优化：

import numpy as np
from gplearn.genetic import SymbolicRegressor
from gplearn.fitness import make_fitness

# 定义自定义适应度函数
def custom_fitness(y, y_pred, w):
    return np.sum(np.abs(y - y_pred))

my_custom_fitness = make_fitness(function=custom_fitness, greater_is_better=False)

# 生成自定义的数据集和目标函数
def my_custom_dataset(n_samples=100, n_features=5):
    X = np.random.rand(n_samples, n_features)  # 自定义数据集，n_features为特征数量
    y = np.sum(X**2, axis=1)  # 自定义目标函数
    return X, y

# 获取自定义数据集
X, y = my_custom_dataset(n_samples=100, n_features=5)

est_gp = SymbolicRegressor(population_size=1000, generations=50, function_set=['add', 'sub', 'mul', 'div'],
                           metric=my_custom_fitness, stopping_criteria=0.01, verbose=1, random_state=42)

est_gp.fit(X, y)

# 输出最佳符号回归方程
print(est_gp._program)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

在这个示例代码中，我们定义了一个自定义数据集生成函数my_custom_dataset和目标函数，并根据实际任务需求生成数据集。然后使用遗传规划算法对数据集进行优化，得到一个最佳的符号回归方程。您可以根据实际情况调整数据集的特征数量、目标函数以及算法参数来完成智能制造优化任务。

十、集成学习算法Python示例代码

1. 使用集成学习算法（Ensemble Learning）完成智能制造提高生产过程中的预测能力任务Python示例代码

集成学习算法在智能制造中可以提高生产过程中的预测能力，通过结合多个基本模型的预测结果，可以获得更准确和稳定的预测结果。以下是一个示例代码，演示了如何使用随机森林（Random Forest）作为集成学习算法来完成智能制造预测任务：

import numpy as np
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 生成模拟的制造生产过程数据
X = np.random.rand(100, 5)  # 模拟5个生产参数
y = np.sum(X ** 2, axis=1)  # 模拟生产过程的目标值

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 使用随机森林作为集成学习算法
rf = RandomForestRegressor(n_estimators=100, random_state=42)
rf.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = rf.predict(X_test)

# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print(f"均方误差：{mse}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

在这个示例代码中，我们使用随机森林（Random Forest）作为集成学习算法，使用模拟的制造生产过程数据来训练模型，并在测试集上进行预测。最后计算均方误差评估预测性能。您可以根据实际情况调整数据集以及算法参数来完成智能制造预测任务。
以下是一个示例代码，根据您提供的数据集和算法参数来完成智能制造预测任务。在这个示例中，我们使用自定义的数据集和根据实际情况调整的随机森林参数来完成预测任务：

import numpy as np
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 自定义数据集和目标函数
def custom_dataset(n_samples=100, n_features=5):
    X = np.random.rand(n_samples, n_features)  # 自定义数据集，n_features为特征数量
    y = np.sum(X**2, axis=1)  # 自定义目标函数
    return X, y

# 获取自定义数据集
X, y = custom_dataset(n_samples=100, n_features=5)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 调整随机森林算法参数
rf = RandomForestRegressor(n_estimators=200, max_depth=10, random_state=42)  # 调整参数为200棵树，最大深度为10
rf.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = rf.predict(X_test)

# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print(f"均方误差：{mse}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

在这个示例代码中，我们定义了一个自定义的数据集生成函数custom_dataset和目标函数，并根据您提供的实际情况调整了随机森林的参数，如树的数量（n_estimators）和最大深度（max_depth）。通过调整参数和自定义数据集，您可以完成智能制造预测任务并获得相应的性能评估。
使用集成学习算法（Ensemble Learning）完成智能制造提高生产过程中的决策准确性任务Python示例代码

2. 使用集成学习算法（Ensemble Learning）完成智能制造提高生产过程中的决策准确性任务

以下是一个示例代码，展示如何使用集成学习算法（Ensemble Learning）完成智能制造提高生产过程中的决策准确性任务：

import numpy as np
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 生成模拟的制造生产过程数据
X = np.random.rand(100, 5)  # 模拟5个生产参数
y = np.random.randint(2, size=100)  # 模拟生产过程的类别

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 使用随机森林和AdaBoost算法作为集成学习算法
rf = RandomForestClassifier(n_estimators=100, random_state=42)
adb = AdaBoostClassifier(n_estimators=50, random_state=42)

# 训练随机森林和AdaBoost模型
rf.fit(X_train, y_train)
adb.fit(X_train, y_train)

# 在测试集上进行预测
y_pred_rf = rf.predict(X_test)
y_pred_adb = adb.predict(X_test)

# 计算预测准确率
accuracy_rf = accuracy_score(y_test, y_pred_rf)
accuracy_adb = accuracy_score(y_test, y_pred_adb)

print(f"随机森林模型准确率：{accuracy_rf}")
print(f"AdaBoost模型准确率：{accuracy_adb}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

在这个示例代码中，我们使用随机森林（Random Forest）和AdaBoost算法作为集成学习算法，使用模拟的制造生产过程数据来训练模型，并在测试集上进行预测。最后计算各个模型的预测准确率。您可以根据实际情况调整数据集和算法参数来完成智能制造中提高决策准确性的任务。
以下是一个示例代码，展示如何根据实际情况调整数据集和算法参数来完成智能制造中提高决策准确性的任务：

import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 自定义数据集生成函数
def custom_dataset(n_samples, n_features):
    X = np.random.rand(n_samples, n_features)  # 自定义数据集，n_features为特征数量
    y = np.random.randint(2, size=n_samples)  # 自定义标签，二分类任务
    return X, y

# 获取自定义数据集
X, y = custom_dataset(n_samples=100, n_features=5)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 调整随机森林算法参数
rf = RandomForestClassifier(n_estimators=200, max_depth=10, random_state=42)  # 调整参数为200棵树，最大深度为10
rf.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = rf.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"准确率：{accuracy}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

在这个示例代码中，我们定义了一个自定义的数据集生成函数custom_dataset和根据实际情况调整了随机森林的参数，如树的数量（n_estimators）和最大深度（max_depth）。通过调整参数和自定义数据集，您可以完成智能制造提高决策准确性的任务并获得相应的性能评估。

十一、异常检测算法Python示例代码

1. 使用异常检测算法完成智能制造监测生产过程中的异常情况提前预警任务基于统计学和机器学习的异常检测Python示例代码

异常检测算法在智能制造中起着关键作用，能够监测生产过程中的异常情况并提前预警，确保生产的正常运行。以下是一个基于统计学和机器学习的异常检测示例代码：

import numpy as np
from sklearn.ensemble import IsolationForest
from sklearn.covariance import EllipticEnvelope
from sklearn.neighbors import LocalOutlierFactor

# 生成模拟的生产过程数据
np.random.seed(42)
X_normal = np.random.normal(0, 1, (1000, 5))  # 正常生产数据
X_outliers = np.random.uniform(0, 1, (50, 5))  # 异常数据

# 合并正常数据和异常数据
X = np.vstack([X_normal, X_outliers])
y = np.hstack([np.zeros(len(X_normal)), np.ones(len(X_outliers)])

# 使用Isolation Forest算法进行异常检测
iforest = IsolationForest(contamination=0.05, random_state=42)
iforest.fit(X)
y_pred_iforest = iforest.predict(X)

# 使用Elliptic Envelope算法进行异常检测
elliptic_env = EllipticEnvelope(contamination=0.05)
elliptic_env.fit(X)
y_pred_elliptic = elliptic_env.predict(X)

# 使用Local Outlier Factor算法进行异常检测
lof = LocalOutlierFactor(contamination=0.05)
y_pred_lof = lof.fit_predict(X)

# 打印异常检测结果
print("Isolation Forest预测结果：", y_pred_iforest)
print("Elliptic Envelope预测结果：", y_pred_elliptic)
print("Local Outlier Factor预测结果：", y_pred_lof)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

在这个示例代码中，我们生成了模拟的生产过程数据，并使用了Isolation Forest、Elliptic Envelope和Local Outlier Factor等算法进行异常检测。您可以根据实际情况调整参数、数据集或尝试其他异常检测算法来监测生产过程中的异常情况。
以下是根据实际情况调整参数、数据集并尝试不同异常检测算法的示例代码：

import numpy as np
from sklearn.ensemble import IsolationForest
from sklearn.covariance import EllipticEnvelope
from sklearn.svm import OneClassSVM
from sklearn.neighbors import LocalOutlierFactor

# 生成模拟的生产过程数据
np.random.seed(42)
X_normal = np.random.normal(0, 1, (1000, 5))  # 正常生产数据
X_outliers = np.random.uniform(0, 1, (50, 5))  # 异常数据

# 合并正常数据和异常数据
X = np.vstack([X_normal, X_outliers])
y = np.hstack([np.zeros(len(X_normal)), np.ones(len(X_outliers)])

# 调整参数并尝试不同的异常检测算法

# Isolation Forest
iforest = IsolationForest(contamination=0.05, random_state=42)
y_pred_iforest = iforest.fit_predict(X)

# Elliptic Envelope
elliptic_env = EllipticEnvelope(contamination=0.05)
y_pred_elliptic = elliptic_env.fit_predict(X)

# One-class SVM
svm = OneClassSVM(nu=0.05)
y_pred_svm = svm.fit_predict(X)

# Local Outlier Factor
lof = LocalOutlierFactor(contamination=0.05)
y_pred_lof = lof.fit_predict(X)

# 打印异常检测结果
print("Isolation Forest预测结果：", y_pred_iforest)
print("Elliptic Envelope预测结果：", y_pred_elliptic)
print("One-class SVM预测结果：", y_pred_svm)
print("Local Outlier Factor预测结果：", y_pred_lof)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

在这个示例代码中，我们使用了Isolation Forest、Elliptic Envelope、One-class SVM和Local Outlier Factor等异常检测算法，您可以根据实际情况调整参数、数据集或尝试其他异常检测算法来监测生产过程中的异常情况。

2. 使用异常检测算法完成智能制造监测生产过程中的异常情况提前预警任务基于深度学习的异常检测Python示例代码

基于深度学习的异常检测在智能制造中具有很大的潜力，其中一种常用的方法是使用自编码器（Autoencoder）进行异常检测。下面是一个使用自编码器进行异常检测并提前预警任务的Python示例代码：

import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.models import Model

# 生成模拟的生产过程数据
np.random.seed(42)
X_normal = np.random.normal(0, 1, (1000, 5))  # 正常生产数据
X_outliers = np.random.uniform(0, 1, (50, 5))  # 异常数据

# 合并正常数据和异常数据
X = np.vstack([X_normal, X_outliers])
y = np.hstack([np.zeros(len(X_normal)), np.ones(len(X_outliers)])

# 构建自编码器模型
input_dim = X.shape[1]

input_layer = Input(shape=(input_dim,))
encoded = Dense(4, activation='relu')(input_layer)
decoded = Dense(input_dim, activation='linear')(encoded)

autoencoder = Model(input_layer, decoded)
autoencoder.compile(optimizer='adam', loss='mse')

# 训练自编码器模型
autoencoder.fit(X, X, epochs=50, batch_size=16, shuffle=True)

# 使用自编码器进行异常检测
reconstructed_X = autoencoder.predict(X)
mse = np.mean(np.square(X - reconstructed_X), axis=1)
threshold = np.percentile(mse, 95)  # 设置阈值为95分位数

# 提前预警任务
y_pred = np.where(mse > threshold, 1, 0)

# 打印异常检测结果
print("异常检测结果：", y_pred)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

在这个示例代码中，我们使用自编码器模型进行异常检测，并根据重构误差（MSE）设置阈值来预警异常情况。您可以根据实际情况调整模型结构、超参数、训练过程等，并尝试其他深度学习模型来实现智能制造监测生产过程中的异常情况并提前预警任务。

十二、遗传编程算法Python示例代码

1. 使用遗传编程算法（Genetic Programming）完成智能制造自动化设计任务Python示例代码

使用遗传编程算法（Genetic Programming）是一种基于生物进化原理的优化算法，常用于复杂问题的自动化设计和优化任务。下面是一个使用遗传编程算法完成智能制造自动化设计任务的Python示例代码：

import numpy as np
import deap.gp as gp
from deap import creator, base, tools, algorithms

# 定义问题
pset = gp.PrimitiveSet("MAIN", 1)
pset.addPrimitive(np.sin, 1)
pset.addPrimitive(np.cos, 1)
pset.addPrimitive(np.add, 2)
pset.addPrimitive(np.subtract, 2)

creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMin)

toolbox = base.Toolbox()
toolbox.register("expr", gp.genHalfAndHalf, pset=pset, min_=1, max_=2)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("compile", gp.compile, pset=pset)

# 定义评价函数
def eval_func(individual):
    func = toolbox.compile(expr=individual)
    error = np.square(np.array([func(x) for x in np.arange(0, 2*np.pi, 0.1)] - np.sin(np.arange(0, 2*np.pi, 0.1))).mean()
    return error,

toolbox.register("evaluate", eval_func)
toolbox.register("select", tools.selTournament, tournsize=3)
toolbox.register("mate", gp.cxOnePoint)
toolbox.register("expr_mut", gp.genFull, min_=0, max_=2)
toolbox.register("mutate", gp.mutUniform, expr=toolbox.expr_mut, pset=pset)

# 遗传编程算法
population_size = 1000
num_generations = 50
cxpb = 0.5
mutpb = 0.2

pop = toolbox.population(n=population_size)
hof = tools.HallOfFame(1)
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("avg", np.mean)
stats.register("min", np.min)

pop, log = algorithms.eaSimple(pop, toolbox, cxpb, mutpb, num_generations, stats=stats, halloffame=hof, verbose=True)

best_individual = hof[0]
print("Best individual:", best_individual)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

在这个示例代码中，我们使用遗传编程算法定义了一个简单的回归问题，通过优化函数的组合来逼近目标函数。您可以根据实际情况定义自己的问题和评价函数，调整算法的参数以及尝试其他进化算法来完成智能制造自动化设计任务。
为了更好地满足您的需求，我们可以尝试定义一个更具体的智能制造自动化设计问题，并使用遗传算法来优化该问题。在这个示例中，我们将考虑一个简单的生产调度问题：在 3 台机器上进行 4 个工件的加工，每个工件有不同的加工时间，目标是最小化所有工件完成加工的总时间。下面是一个用遗传算法求解该问题的示例代码：

import numpy as np
from deap import creator, base, tools, algorithms

# 定义问题
def eval_func(individual):
    schedule = []
    for machine in range(3):
        machine_schedule = []
        start_time = 0
        for task in individual:
            machine_schedule.append((task, start_time))
            start_time += task
        schedule.append(machine_schedule)
    
    completion_times = [max([machine_schedule[-1][1] for machine_schedule in schedule])]
    return completion_times,

creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", list, fitness=creator.FitnessMin)

toolbox = base.Toolbox()
toolbox.register("permutation", np.random.permutation, 4)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.permutation)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("evaluate", eval_func)
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.05)
toolbox.register("select", tools.selTournament, tournsize=3)

population_size = 100
num_generations = 50
cxpb = 0.8
mutpb = 0.2

pop = toolbox.population(n=population_size)
hof = tools.HallOfFame(1)
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("avg", np.mean)
stats.register("min", np.min)

pop, log = algorithms.eaSimple(pop, toolbox, cxpb, mutpb, num_generations, stats=stats, halloffame=hof, verbose=True)

best_schedule = hof[0]
print("Best schedule:", best_schedule)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

在这个示例代码中，我们通过定义评价函数来求解一个简单的生产调度问题。您可以根据实际情况定制自己的智能制造自动化设计问题，并调整遗传算法的参数以及尝试其他进化算法来解决这个问题。

2. 使用遗传编程算法（Genetic Programming）完成智能制造优化控制策略任务Python示例代码

要使用遗传编程算法（Genetic Programming）来完成智能制造优化控制策略任务，我们可以考虑一个简单的示例问题：设计一个控制策略来最大化生产线上的产量，同时最小化生产成本。下面是一个用遗传编程算法解决该问题的示例代码：

import numpy as np
from deap import creator, base, tools, gp, algorithms

# 创建一个新的遗传编程程序
pset = gp.PrimitiveSet("MAIN", arity=1)
pset.addPrimitive(np.add, arity=2)
pset.addPrimitive(np.subtract, arity=2)
pset.addPrimitive(np.multiply, arity=2)
pset.addPrimitive(np.divide, arity=2)
pset.addPrimitive(np.sin, arity=1)
pset.addPrimitive(np.cos, arity=1)
pset.addPrimitive(np.exp, arity=1)
pset.addPrimitive(np.log, arity=1)
pset.addEphemeralConstant("rand", lambda: np.random.uniform(-1, 1))

creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMax)

toolbox = base.Toolbox()
toolbox.register("expr", gp.genFull, pset=pset, min_=1, max_=2)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("compile", gp.compile, pset=pset)
toolbox.register("evaluate", evaluate_production_control)
toolbox.register("select", tools.selTournament, tournsize=3)
toolbox.register("mate", gp.cxOnePoint)
toolbox.register("expr_mut", gp.genFull, min_=0, max_=2)
toolbox.register("mutate", gp.mutUniform, expr=toolbox.expr_mut, pset=pset)

# 定义评价函数
def evaluate_production_control(individual):
    # 模拟生产控制策略，计算产量和成本
    control_strategy = toolbox.compile(expr=individual)
    production = control_strategy()
    
    # 简化成本模型，假设产量和成本关系为线性
    cost = -0.5 * production
    
    return production, cost

# 遗传编程算法
population_size = 1000
num_generations = 50
cxpb = 0.5
mutpb = 0.2

pop = toolbox.population(n=population_size)
hof = tools.HallOfFame(1)
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("avg", np.mean)
stats.register("min", np.min)

pop, log = algorithms.eaSimple(pop, toolbox, cxpb, mutpb, num_generations, stats=stats, halloffame=hof, verbose=True)

best_control_strategy = hof[0]
best_production, best_cost = evaluate_production_control(best_control_strategy)
print("Best production control strategy:", best_control_strategy)
print("Best production:", best_production)
print("Corresponding cost:", best_cost)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

在这个示例代码中，我们使用遗传编程算法来设计一个生产控制策略，以最大化产量并最小化成本。您可以根据实际问题定制自己的优化目标和控制策略，并调整算法参数来解决智能制造优化控制策略任务。
当定制智能制造优化控制策略时，您可以考虑以下示例问题和相应的示例代码：

问题描述：
假设有一个生产线，生产线上有三个工作站（A、B、C），每个工作站可以生产不同种类的产品，但不同种类的产品需要经过不同的工作站进行加工。每个工作站有不同的加工速度和成本，同时产品在每个工作站的处理时间也不同。您需要设计一个智能制造优化控制策略，以最大化整体产量并最小化生产成本。

示例代码：

import numpy as np
from deap import creator, base, tools, gp, algorithms

# 创建一个新的遗传编程程序
pset = gp.PrimitiveSetTyped("MAIN", [float, float, float], float)
pset.addPrimitive(max, [float, float, float], float)
pset.addPrimitive(min, [float, float, float], float)
pset.addPrimitive(np.add, [float, float], float)
pset.addPrimitive(np.subtract, [float, float], float)
pset.addPrimitive(np.multiply, [float, float], float)
pset.addPrimitive(np.divide, [float, float], float)

creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMax)

toolbox = base.Toolbox()
toolbox.register("expr", gp.genFull, pset=pset, min_=1, max_=3)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("compile", gp.compile, pset=pset)
toolbox.register("evaluate", evaluate_production_control)
toolbox.register("select", tools.selTournament, tournsize=3)
toolbox.register("mate", gp.cxOnePoint)
toolbox.register("expr_mut", gp.genFull, min_=0, max=3)
toolbox.register("mutate", gp.mutUniform, expr=toolbox.expr_mut, pset=pset)

# 定义评价函数
def evaluate_production_control(individual):
    # 模拟生产控制策略，计算产量和成本
    control_strategy = toolbox.compile(expr=individual)
    
    # 简化模拟生产过程
    processing_times = [1.0, 1.5, 2.0]  # 三个工作站的平均处理时间
    processing_costs = [10.0, 15.0, 20.0]  # 三个工作站的平均成本
    product_demand = 1000  # 产品需求量
    
    total_production = control_strategy(*processing_times)
    total_cost = sum([control_strategy(*processing_times) * processing_costs[i] for i in range(3)])
    
    if total_cost > 1000:
        total_production = 0  # 如果成本超过1000，产量置为0
    
    return total_production, total_cost

# 遗传编程算法
population_size = 100
num_generations = 50
cxpb = 0.5
mutpb = 0.2

pop = toolbox.population(n=population_size)
hof = tools.HallOfFame(1)
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("avg", np.mean)
stats.register("min", np.min)

pop, log = algorithms.eaSimple(pop, toolbox, cxpb, mutpb, num_generations, stats=stats, halloffame=hof, verbose=True)

best_control_strategy = hof[0]
best_production, best_cost = evaluate_production_control(best_control_strategy)
print("Best production control strategy:", best_control_strategy)
print("Best production:", best_production)
print("Corresponding cost:", best_cost)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

在这个示例代码中，我们根据任务描述定制了一个智能制造优化控制策略问题，并使用遗传编程算法来解决问题。您可以根据实际问题定制自己的优化目标和控制策略，并根据需要调整算法参数。

十三、时间序列分析算法Python示例代码

当涉及智能制造分析和预测生产过程中的时间序列数据时，ARMA（AutoRegressive Moving Average）是一个常用的算法。下面是一个简单的Python示例代码，演示如何使用ARMA模型对时间序列数据进行分析和预测。

1. 使用ARMA模型算法完成智能制造对时间序列数据进行分析和预测任务Python示例代码

智能制造分析和预测生产过程中的时间序列数据时，ARMA（AutoRegressive Moving Average）是一个常用的算法**
下面是一个简单的Python示例代码，演示如何使用ARMA模型对时间序列数据进行分析和预测：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA

# 生成示例时间序列数据
np.random.seed(42)
time_series = pd.Series(np.random.randn(1000), index=pd.date_range('2020-01-01', periods=1000))

# 拟合ARMA模型
# 这里假设选择AR阶数为2，MA阶数为1
model = ARIMA(time_series, order=(2, 0, 1))  # 注意这里的order参数中，d=0表示不进行差分处理

model_fit = model.fit()

# 绘制原始数据和ARMA模型拟合数据
plt.figure(figsize=(12, 6))
plt.plot(time_series, label='Original Data')
plt.plot(model_fit.fittedvalues, color='red', label='ARMA Model')
plt.legend()
plt.show()

# 预测未来数据
future_steps = 50
forecast = model_fit.forecast(steps=future_steps)

# 绘制未来预测数据
plt.figure(figsize=(12, 6))
plt.plot(time_series, label='Original Data')
plt.plot(pd.date_range(start=time_series.index[-1], periods=future_steps+1, freq=time_series.index.freq)[1:], forecast, color='green', label='Forecast')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

在这个示例代码中，我们使用ARMA模型对时间序列数据进行了分析和预测。您可以根据实际情况调整AR和MA阶数，以获得更好的拟合效果和预测结果。

在时间序列分析中，调整AR和MA阶数是非常重要的，可以帮助我们获得更好的拟合效果和预测结果。以下是一个示例代码，展示如何根据实际情况选择合适的AR和MA阶数，并进行模型拟合和预测：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA

# 生成示例时间序列数据
np.random.seed(42)
time_series = pd.Series(np.random.randn(1000), index=pd.date_range('2020-01-01', periods=1000))

# 根据ACF和PACF图形选择合适的AR和MA阶数
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(time_series, lags=20)
plot_pacf(time_series, lags=20)
plt.show()

# 假设选择AR阶数为2，MA阶数为1
model = ARIMA(time_series, order=(2, 0, 1))

# 拟合ARIMA模型
model_fit = model.fit()

# 绘制原始数据和ARIMA模型拟合数据
plt.figure(figsize=(12, 6))
plt.plot(time_series, label='Original Data')
plt.plot(model_fit.fittedvalues, color='red', label='ARIMA Model')
plt.legend()
plt.show()

# 预测未来数据
future_steps = 50
forecast = model_fit.forecast(steps=future_steps)

# 绘制未来预测数据
plt.figure(figsize=(12, 6))
plt.plot(time_series, label='Original Data')
plt.plot(pd.date_range(start=time_series.index[-1], periods=future_steps+1, freq=time_series.index.freq)[1:], forecast, color='green', label='Forecast')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

在这个示例代码中，我们根据ACF和PACF图形选择了AR阶数为2，MA阶数为1，并根据选择的参数进行了ARIMA模型的拟合和预测。您可以根据实际数据的情况，进一步调整AR和MA阶数，以获得更好的拟合效果和预测结果。

2. 使用ARIMA模型算法完成智能制造对时间序列数据进行分析和预测任务Python示例代码

当涉及智能制造分析和预测生产过程中的时间序列数据时，ARIMA（AutoRegressive Integrated Moving Average）是一个常用的算法。下面是一个简单的Python示例代码，演示如何使用ARIMA模型对时间序列数据进行分析和预测：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.stattools import adfuller

# 生成示例时间序列数据
np.random.seed(42)
time_series = pd.Series(np.random.randn(1000), index=pd.date_range('2020-01-01', periods=1000))

# 函数：ADF检验（单位根检验）
def adf_test(timeseries):
    result = adfuller(timeseries, autolag='AIC')
    print('ADF Statistic: %f' % result[0])
    print('p-value: %f' % result[1])

# 检验时间序列数据的平稳性
adf_test(time_series)

# 拟合ARIMA模型
model = ARIMA(time_series, order=(5,1,0))  # 这里选择ARIMA模型的(p,d,q)参数
model_fit = model.fit()

# 绘制原始数据和预测数据
plt.figure(figsize=(12, 6))
plt.plot(time_series, label='Original Data')
plt.plot(model_fit.fittedvalues, color='red', label='ARIMA Model')
plt.legend()
plt.show()

# 预测未来数据
future_steps = 50
forecast = model_fit.forecast(steps=future_steps)

# 绘制未来预测数据
plt.figure(figsize=(12, 6))
plt.plot(time_series, label='Original Data')
plt.plot(pd.date_range(start=time_series.index[-1], periods=future_steps+1, freq=time_series.index.freq)[1:], forecast, color='green', label='Forecast')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

在这个示例代码中，我们首先生成了一个示例时间序列数据，然后进行了ADF检验以检验数据的平稳性。接下来，我们拟合了一个ARIMA模型，并绘制了原始数据和模型拟合数据的对比图。最后，我们使用拟合的模型进行未来数据的预测，并绘制了未来预测数据的图表。

您可以根据实际情况调整参数和模型选择，以适应您的时间序列数据和预测需求。
当根据实际情况调整参数和模型选择时，您可以根据数据的特点和问题的需求来选择合适的时间序列模型和参数。以下是一个示例代码，演示如何根据实际情况进行参数调整和模型选择，以适应不同的时间序列数据和预测需求：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.stattools import adfuller

# 生成示例时间序列数据
np.random.seed(42)
time_series = pd.Series(np.random.randn(1000), index=pd.date_range('2020-01-01', periods=1000))

# 函数：ADF检验（单位根检验）
def adf_test(timeseries):
    result = adfuller(timeseries, autolag='AIC')
    print('ADF Statistic: %f' % result[0])
    print('p-value: %f' % result[1])

# 检验时间序列数据的平稳性
adf_test(time_series)

# 根据实际情况调整参数和模型选择
# 例如，根据ADF检验结果判断数据是否平稳，若不平稳则可以考虑使用差分（d）来处理数据
# 根据ACF和PACF图形以及信息准则（如AIC或BIC）来选择合适的AR和MA阶数

# 示例：如果数据需要做一阶差分处理
time_series_diff = time_series.diff().dropna()

# 示例：根据ACF和PACF图形，选择AR和MA阶数
# 这里假设选择AR阶数为2，MA阶数为1
model = ARIMA(time_series_diff, order=(2, 1, 1))

# 拟合ARIMA模型
model_fit = model.fit()

# 绘制原始数据和预测数据
plt.figure(figsize=(12, 6))
plt.plot(time_series_diff, label='Original Data (Differenced)')
plt.plot(model_fit.fittedvalues, color='red', label='ARIMA Model')
plt.legend()
plt.show()

# 预测未来数据
future_steps = 50
forecast = model_fit.forecast(steps=future_steps)

# 绘制未来预测数据
plt.figure(figsize=(12, 6))
plt.plot(time_series_diff, label='Original Data (Differenced)')
plt.plot(pd.date_range(start=time_series_diff.index[-1], periods=future_steps+1, freq=time_series_diff.index.freq)[1:], forecast, color='green', label='Forecast')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

在这个示例代码中，我们根据实际情况进行了参数调整和模型选择，包括根据ADF检验结果进行一阶差分处理，根据ACF和PACF图形选择合适的AR和MA阶数。您可以根据数据的具体情况和需求进一步调整模型参数，以适应不同的时间序列数据和预测需求。

十四、深度强化学习算法Python示例代码

深度强化学习（Deep Reinforcement Learning, DRL）结合了深度学习和强化学习的技术，可以实现在智能制造中更复杂、更智能的控制策略和优化方法。

1. 基于Python和TensorFlow的深度强化学习算法完成智能制造更复杂、更智能的控制策略和优化任务Python示例代码

演示如何使用DRL在一个虚拟环境中构建和训练智能代理。

首先，您需要安装必要的库，例如TensorFlow和OpenAI Gym：

pip install tensorflow gym
1

接下来是一个简单的深度强化学习示例代码：

import numpy as np
import tensorflow as tf
import gym

# 创建一个简单的神经网络模型
class DQN(tf.keras.Model):
    def __init__(self, num_actions):
        super(DQN, self).__init__()
        self.dense1 = tf.keras.layers.Dense(128, activation='relu')
        self.dense2 = tf.keras.layers.Dense(num_actions)

    def call(self, inputs):
        x = self.dense1(inputs)
        return self.dense2(x)

# 创建一个深度强化学习代理
class DQNAgent:
    def __init__(self, num_actions):
        self.model = DQN(num_actions)
        self.optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)

    def select_action(self, state, epsilon):
        if np.random.rand() < epsilon:
            return np.random.randint(2)  # 在这里假设有两个动作
        else:
            return np.argmax(self.model.predict(state)[0])

    def train(self, state, action, reward, next_state, done):
        with tf.GradientTape() as tape:
            q_values = self.model(state, training=True)
            next_q_values = self.model(next_state, training=False)
            target = reward + (1 - done) * 0.99 * tf.reduce_max(next_q_values, axis=1)
            action_mask = tf.one_hot(action, 2)  # 在这里假设有两个动作
            action_q_values = tf.reduce_sum(tf.multiply(q_values, action_mask), axis=1)
            loss = tf.reduce_mean(tf.square(action_q_values - target))
        
        grads = tape.gradient(loss, self.model.trainable_variables)
        self.optimizer.apply_gradients(zip(grads, self.model.trainable_variables))
        
# 创建一个虚拟环境
env = gym.make('CartPole-v1')

# 初始化代理和参数
agent = DQNAgent(num_actions=2)
epsilon = 1.0

# 训练代理
for episode in range(1000):
    state = env.reset()
    state = np.expand_dims(state, axis=0)
    episode_reward = 0
    
    while True:
        epsilon *= 0.995
        action = agent.select_action(state, epsilon)
        next_state, reward, done, _ = env.step(action)
        next_state = np.expand_dims(next_state, axis=0)
        
        agent.train(state, action, reward, next_state, done)
        
        state = next_state
        episode_reward += reward
        
        if done:
            print(f"Episode: {episode + 1}, Reward: {episode_reward}")
            break
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

这个示例代码使用DQN算法在OpenAI Gym中的CartPole环境上训练一个智能代理。您可以根据需要调整神经网络模型和训练参数，以适应不同的智能制造场景。

2. 基于更深的神经网络模型算法完成智能制造更复杂更智能的控制策略和优化任务Python示例代码

以下是一个稍微复杂的示例代码，它使用了一个更深的神经网络模型和其他一些训练参数的调整，以适应不同的智能制造场景，完成智能制造更复杂、更智能的控制策略和优化任务：

import numpy as np
import tensorflow as tf
import gym

# 创建一个深度强化学习代理
class DQNAgent:
    def __init__(self, num_actions, state_dim):
        self.model = tf.keras.Sequential([
            tf.keras.layers.Dense(64, activation='relu', input_shape=state_dim),
            tf.keras.layers.Dense(64, activation='relu'),
            tf.keras.layers.Dense(num_actions)
        ])
        self.optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)

    def select_action(self, state, epsilon):
        if np.random.rand() < epsilon:
            return np.random.randint(2)  # 在这里假设有两个动作
        else:
            q_values = self.model.predict(state)
            return np.argmax(q_values[0])

    def train(self, state, action, reward, next_state, done):
        with tf.GradientTape() as tape:
            q_values = self.model(state, training=True)
            next_q_values = self.model(next_state, training=False)
            target = reward + (1 - done) * 0.99 * tf.reduce_max(next_q_values, axis=1)
            action_mask = tf.one_hot(action, 2)  # 在这里假设有两个动作
            action_q_values = tf.reduce_sum(tf.multiply(q_values, action_mask), axis=1)
            loss = tf.reduce_mean(tf.square(action_q_values - target))
        
        grads = tape.gradient(loss, self.model.trainable_variables)
        self.optimizer.apply_gradients(zip(grads, self.model.trainable_variables))

# 创建一个虚拟环境
env = gym.make('MountainCar-v0')

# 初始化代理和参数
agent = DQNAgent(num_actions=2, state_dim=(2,))
epsilon = 1.0

# 训练代理
for episode in range(1000):
    state = env.reset()
    state = np.expand_dims(state, axis=0)
    episode_reward = 0
    
    while True:
        epsilon *= 0.995
        action = agent.select_action(state, epsilon)
        next_state, reward, done, _ = env.step(action)
        next_state = np.expand_dims(next_state, axis=0)
        
        agent.train(state, action, reward, next_state, done)
        
        state = next_state
        episode_reward += reward
        
        if done:
            print(f"Episode: {episode + 1}, Reward: {episode_reward}")
            break
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

这个示例代码修改了神经网络模型的结构，增加了两个隐藏层，每个隐藏层有64个神经元。此外，修改了虚拟环境为MountainCar-v0，这是一个在OpenAI Gym中经典的智能制造场景。

您可以根据自己的需要和具体场景进一步调整神经网络模型结构、训练参数、环境等，以实现更好的性能和适应性。这个示例代码是一个起点，您可以根据实际情况进行定制和优化。

十五、知识点归纳

AI在智能制造中的应用是一个非常广泛和重要的领域。以下是基于AI的智能制造技术中的一些经典算法以及与Python实践相关的技术点的归纳：

1. 监督学习：监督学习是一种常见的机器学习方法，用于从已标记的数据中学习模型。在智能制造中，监督学习可以用于机器视觉、生产优化等任务。Python中的scikit-learn库提供了丰富的监督学习算法实现。

2. 无监督学习：无监督学习是一种训练模型而无需标记数据的机器学习方法。在智能制造中，无监督学习可以用于异常检测、聚类分析等任务。Python中的scikit-learn库也支持无监督学习算法。

3. 强化学习：强化学习是一种通过代理与环境的交互来学习最优决策策略的机器学习方法。在智能制造中，强化学习可以用于控制系统优化、资源调度等任务。Python中的TensorFlow、PyTorch等库提供了强化学习算法的实现。

4. 遗传算法：遗传算法是一种优化算法，模拟生物进化过程来搜索最优解。在智能制造中，遗传算法可以用于优化参数、设计问题等。Python中的遗传算法库DEAP提供了实现遗传算法的功能。

5. 深度学习：深度学习是一种基于神经网络的机器学习方法，可以用于处理大规模复杂数据和学习复杂模式。在智能制造中，深度学习可以用于图像识别、文本处理、预测建模等任务。Python中的TensorFlow、PyTorch等库提供了深度学习算法的实现。

6. 强化学习算法实践技术点：在实践中，需要注意选择合适的强化学习算法（如Q-learning、DQN、Policy Gradient等）、设计合适的状态表示和动作空间、调整奖励函数以及调优超参数等技术点。此外，可以使用OpenAI Gym等开源平台进行环境建模和测试。

7. 数据处理与特征工程：在智能制造中，数据处理和特征工程是非常重要的步骤，可以帮助提取有用的信息和特征。Python中的pandas、NumPy等库可以用于数据处理和特征工程。

8. 模型评估与优化：在实际应用中，需要对模型进行评估和调优，以提高性能和泛化能力。交叉验证、超参数调优等技术在智能制造中也非常重要。Python中的scikit-learn库提供了丰富的模型评估和优化工具。

这些技术点是基于AI的智能制造中常用的一些算法和实践技术点，希望能为您对AI在智能制造中的应用有所帮助。