数学建模--Matlab求解线性规划问题&&两种类型&&实际应用_matlab线性规划问题

1.约束条件的符号一致

（1）约束条件的符号一致的意思就是指的是这个约束条件里面的，像这个下面的实例里面的三个约束条件，都是小于号，这个我称之为约束条件符号一致；

（2）下面的就是上面的这个线性规划问题的代码，我们首先要把这个目标函数的系数矩阵表示出来，就是这个代码里面的第三行的c向量，然后表示这个约束条件的系数矩阵，因为第三个约束条件是x2<=7.因此这个x1前面的系数就是0，b向量表示的就是这个等号右边的数据；

clc,clear;
 
pro=optimproblem("ObjectiveSense","max");
 
c=[4,3];
 
a=[2,1;1,1;0,1];
 
b=[10;8;7];
 
x=optimvar("x",2,"LowerBound",0);
 
pro.Objective=c*x;
 
pro.Constraints=a*x<=b;
 
[s,v]=solve(pro);
 
xx=s.x

 （3）optimvar表示的就是创建优化变量，在这个问题里面，x1和x2就是优化变量，因为这个优化变量的最小值是0，所以在这个代码里面，我们使用这个lowerbound表示的就是最小边界值，2表示的就是这个问题里面的优化变量的数量是两个；

（4）pro就是我们给这个问题起的一个名字，这个名字变量是可以随意命名的，但是这个过程中的名字要保持一致，c*x表示的就是这个目标函数，我们通过这个矩阵的乘法可以得到这个目标函数

（5）注意事项：上面这个里面老师讲解的时候使用的就是乘号，但是我自己认为应该使用点乘的操作，因为之前我们说过这个向量的乘法，应该使用点乘，但是这个如果使用点乘就会报错；

报错的原因就是这优化变量矩阵x表示的就是一个列向量，就是这个x1x2实际上是2行1列的矩阵，这个点乘的时候矩阵的维数（几行几列）必须是一样的，这个也是报错的提示出来的错误信息；

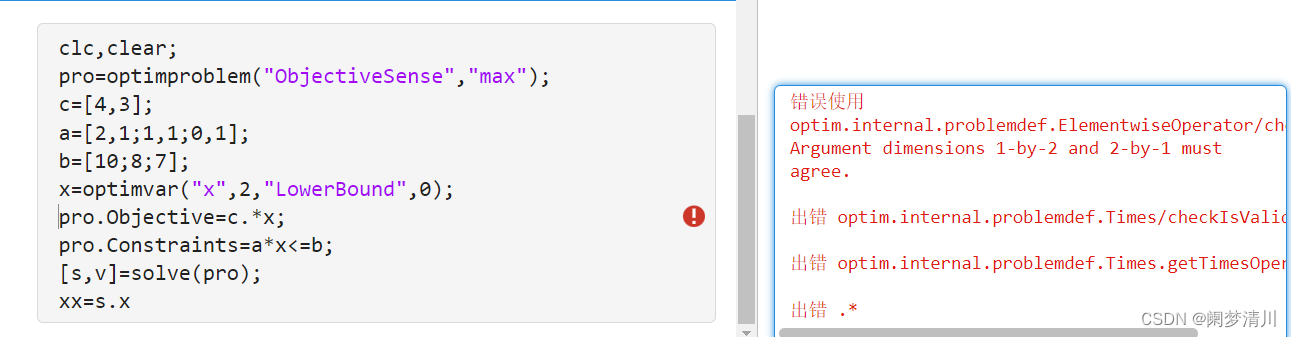
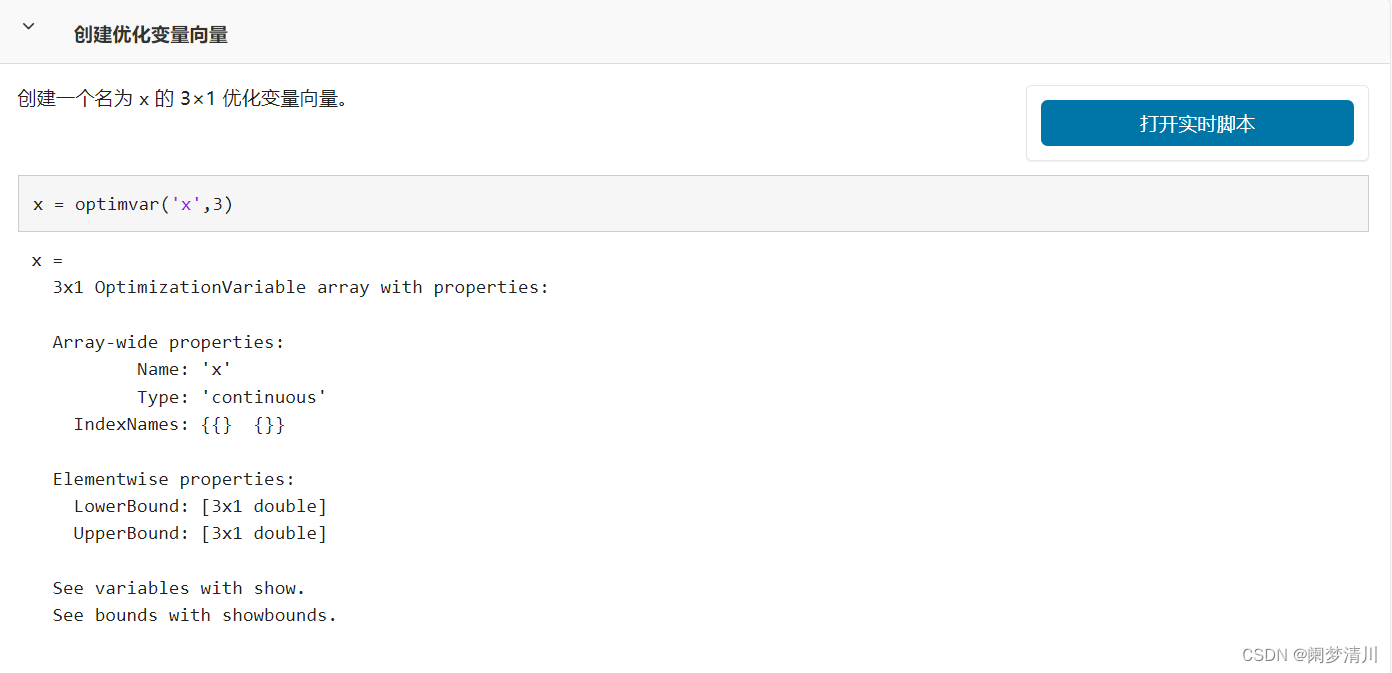
（6）为什么会出现这个情况，我们可以打开这个optimvar函数的帮助文档，这个里面就有一个例子，说的就是这个创建的是3*1的矩阵，因此，我们可以理解为这个函数创建的矩阵默认就是列向量；

实际上这个matlab里面输入一个向量，这个向量会被默认为是行向量，这个和该函数的默认方式还是有所区别的；

 

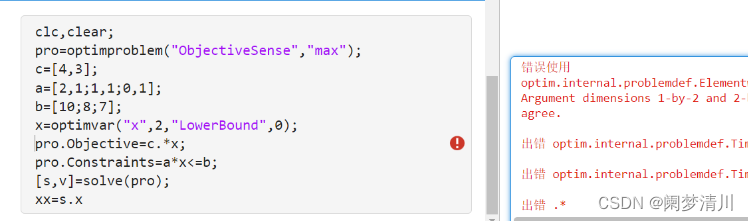
（7）同理这个约束条件，就是a*x<=b这个就是组合之后会出现我们现在的约束条件，使用solve函数解决这个pro问题，返回值两个，一个就是s，即两个优化变量的值，val指的就是这个目标函数的最值；

因为这个求解的是最大值，但是这个默认的是最小值，因此在这个optimproblem函数里面，我们使用到了这个objectsence表示的就是相反的意思，意思就是原来默认的是求解最小值，我们使用这个指令之后就会求解出来这个目标函数的最大值，这个也是不需要我们自己记住的，因为这个在我们键入这个optimproblem之后，这个会默认的显示出来，我们只需要使用tab键补充完整就可以了

 

2.约束条件的符号不一致

（2）这个想必你就已经知道了，这个符号不一致的时候，就是需要我们挨个把这个约束条件给罗列出来，而且这个matlab里面不支持这种符号不相同的方程组，只能放在不同的约束条件里面，无法使用一个约束条件统一表示出来，但是python可以；

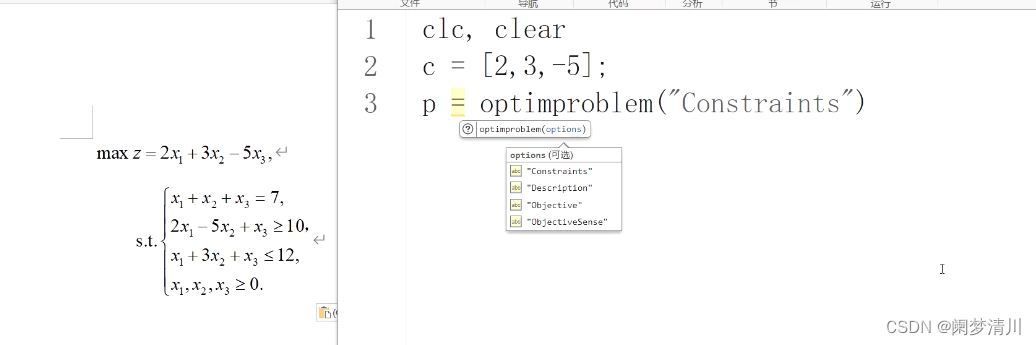
（2）这个约束条件是写出来了3个，sum就是求解这三个优化变量的和，第二个和第三个就是普通的大于小于条件约束，这个变量x1中的1必须加上括号，否则运行的时候这个系统就会报错，表示这个变量无法识别；

 

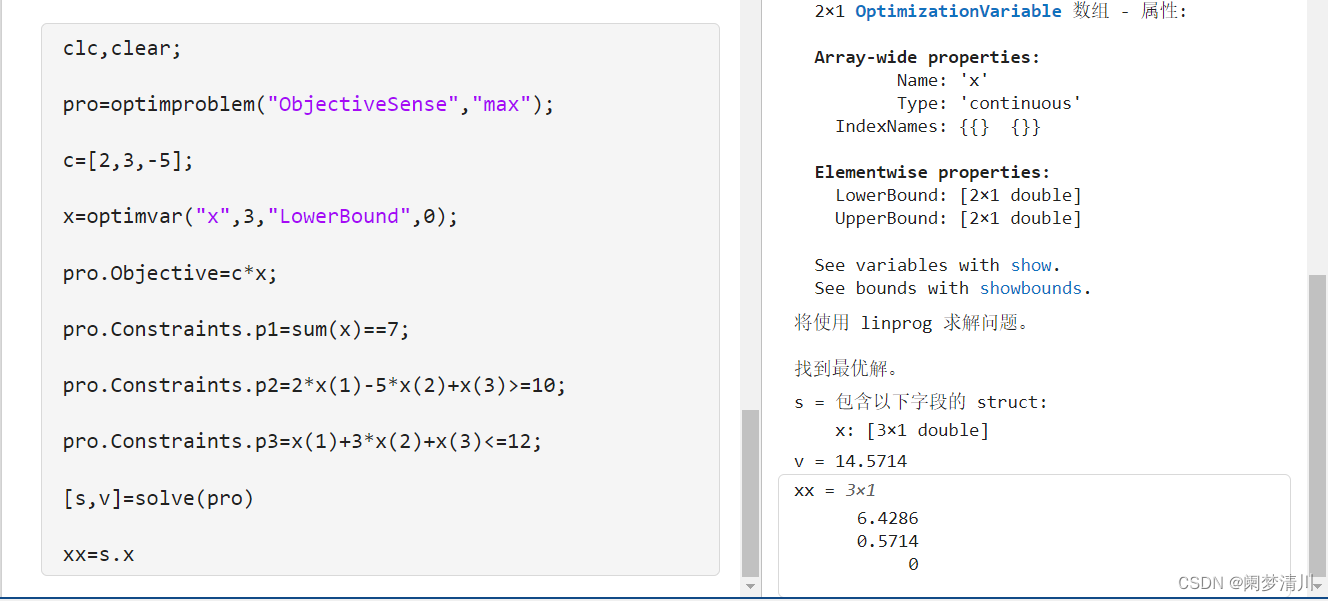
（3）p1,p2,p3就是我们给这个约束条件起的名字，上一个题目是只有一个式子就可以表示这三个约束条件，因此我们只写出来了pro.constraints没有写后面的，但是这个里面我们使用的是多个式子，方便区分，我们必须给这三个约束条件命名；

clc,clear;
 
pro=optimproblem("ObjectiveSense","max");
 
c=[2,3,-5];
 
x=optimvar("x",3,"LowerBound",0);
 
pro.Objective=c*x;
 
pro.Constraints.p1=sum(x)==7;
 
pro.Constraints.p2=2*x(1)-5*x(2)+x(3)>=10;
 
pro.Constraints.p3=x(1)+3*x(2)+x(3)<=12;
 
[s,v]=solve(pro)
 
xx=s.x

3.模型的应用

（1）这个就是一个仓库的租借问题；

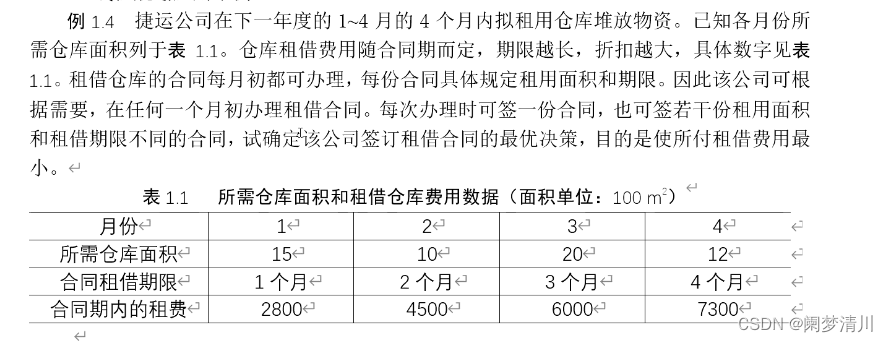
 （2）

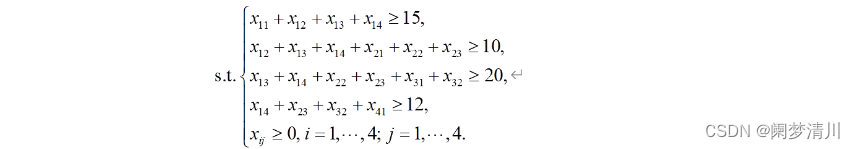
（3）我们通过对于这个模型的分析决定定义4*4的矩阵，这个每一个元素的含义上面有相应的说明，我们使用的就是无符号的，纯数学语言，使用通式进行表示这些变量；

 

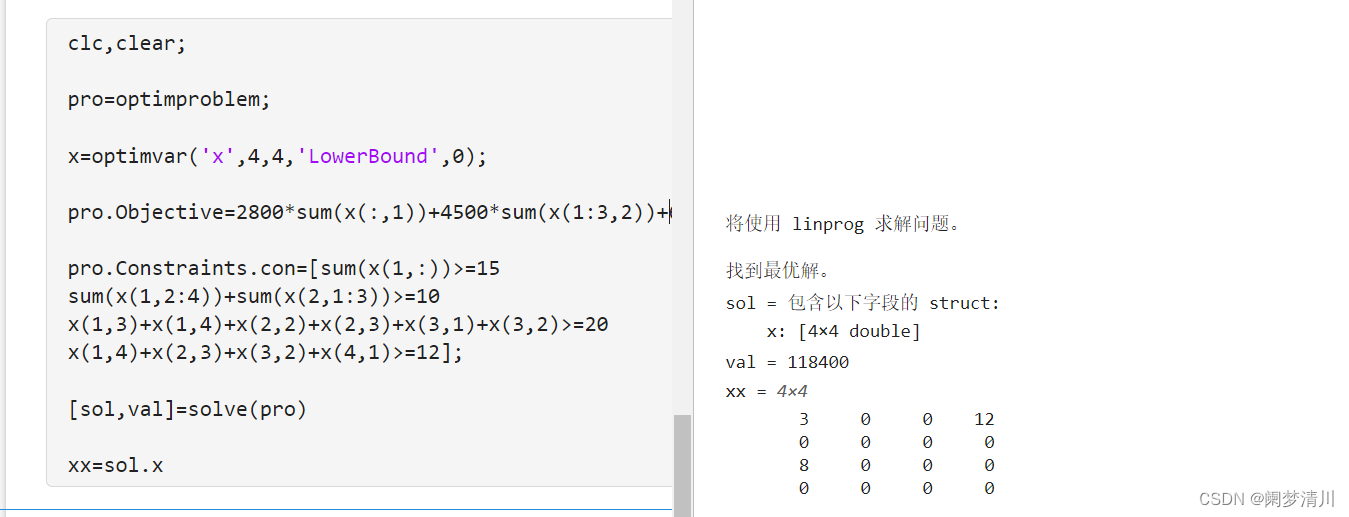
（4）这个里面出现了一种符号，x(1,2:4)表示的就是这个矩阵里面的第一行的第二个，第三个和第四个，前面的sum元素就表示对于这三个元素进行求和；

x(1,:)这个就是取出来第一行的元素，哪些列呢，就是1,2,3,4,5一直到最后，我们就可以使用这个里面的冒号进行标识；

（5） 这个里面的问题会有什么，这个下面的就是我自己遇到的问题，这个目标函数我最开始是写了两行的，就是下面这样的，但是无法求解出来正确的结果，这个不是我们语法问题，而是这个换行的格式问题，我们可以写在一行，也可以使用下面的方法：即把加号放在末尾，加上三个点，系统会识别为蓝色的，这样就可以把这两行的内容连接在一起了；

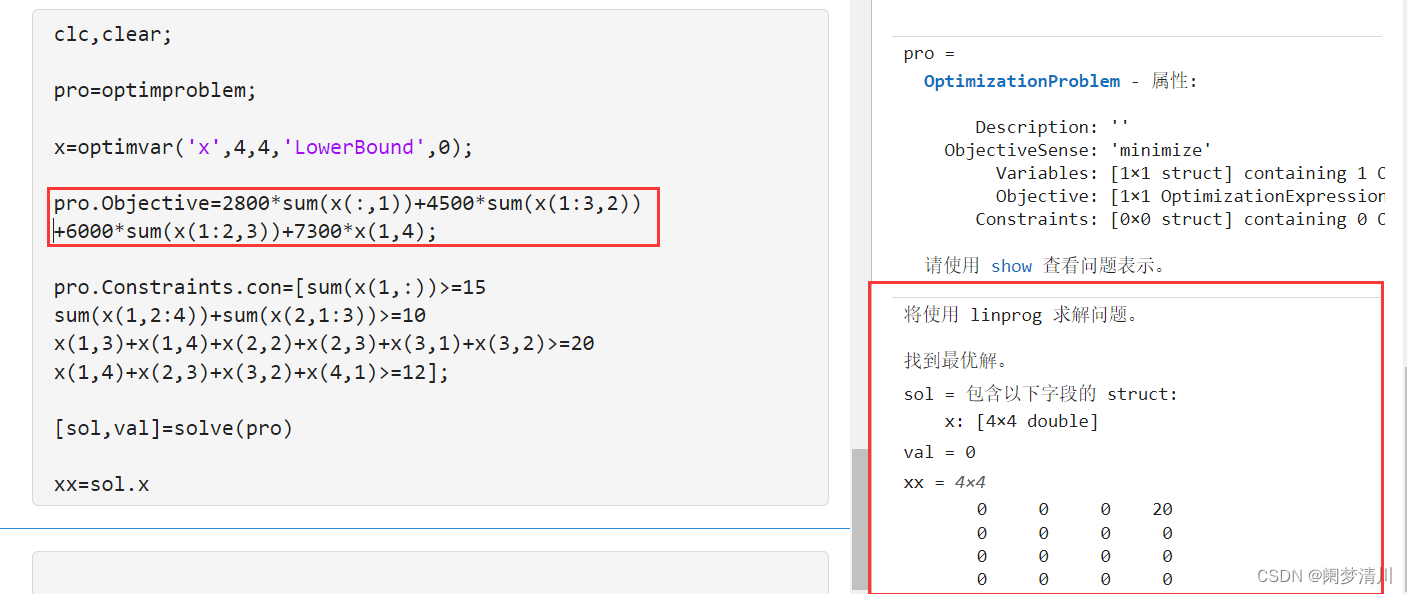
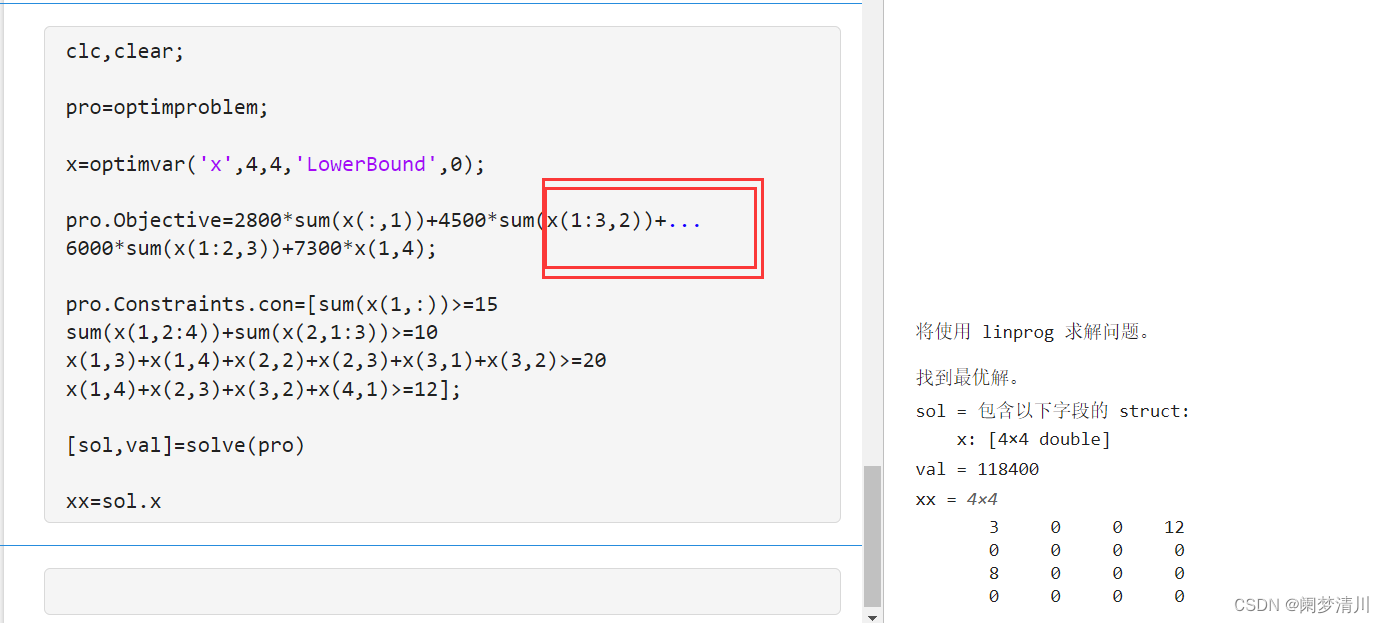
（6）代码自测：

clc,clear;
 
pro=optimproblem;
 
x=optimvar('x',4,4,'LowerBound',0);
 
pro.Objective=2800*sum(x(:,1))+4500*sum(x(1:3,2))+...
6000*sum(x(1:2,3))+7300*x(1,4);
pro.Constraints.con=[sum(x(1,:))>=15
sum(x(1,2:4))+sum(x(2,1:3))>=10
x(1,3)+x(1,4)+x(2,2)+x(2,3)+x(3,1)+x(3,2)>=20
x(1,4)+x(2,3)+x(3,2)+x(4,1)>=12];
 
[sol,val]=solve(pro)
 
xx=sol.x