- 1oracle的merge into操作详解_merge into oracle
- 2docker build 没有网络 执行dockerfile中yum报错 curl#6 - “Could not resolve host: mirrorlist.centos.org 解决方法_curl#6 - "could not resolve host: mirrorlist.cento
- 3校园报修维修小程序,微信小程序报修系统,微信小程序宿舍报修系统毕设作品_校园维修的意义
- 4工业互联网的人工智能与大数据融合应用
- 5大模型训练:文件保存类型与优化策略_大模型训练文件
- 6聚类篇——(三)K-Medoids聚类
- 7(19-2)操作国产大模型:LangChain与百度千帆大模型实践_qianfanllmendpoint
- 8python如何停止子线程_【已解决】python 如何结束子线程呢
- 9100份PHP计算机毕业设计项目推荐(源码+论文+PPT)_php结课项目
- 10Python+OpenCV之图片批处理(一)_opencv批量读取图片python
FPGA - DFT(离散傅里叶变换)—FFT(快速傅里叶变化)_基于fpga的256点dft傅里叶变换verilog实现
赞
踩
一,DFT(离散傅里叶变换原理)
1,DFT(离散傅里叶变换原理)理论简介
在数字信号处理中有一个基本概念:
如果信号在频域是离散的,则该信号在时域就表现为周期性的时间函数;相反,如果信号在时域是离散的,则该信号在频域必然表现为周期性的频率函数。那么如果时域信号不仅是离散的,而且是周期的,那么由于它在时域离散,其频谱必是周期的;如果在时域是周期的,则相应的频谱必是离散的。换句话说,一个离散周期时间序列,它一定具有既是周期又是离散的频谱。还可以得出一个结论:一个域的离散就必然造成另一个域的周期延拓,这种离散变换,本质上都是周期的。
一个连续信号经过理想采样后的表达式为:

其频谱函数Xa(jΩ)是上式的傅里叶变换,容易得出其傅里叶变换为:
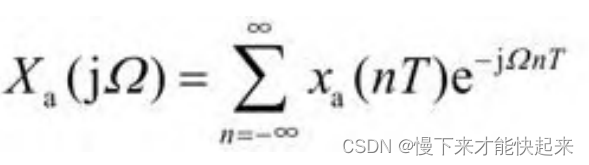
式中,Ω为模拟角频率,单位为rad/s,它与数字角频率ω之间的关系为ω=ΩT。对于数字信号来说,处理的信号其实是一个数字序列。因此,可用x(n)代替xa(nT),同时用X(ejω)代替xa(jω/T),则可以得到时域离散信号的频谱表达式,即:

显然,X(ejω)是以2π为周期的函数。上式也印证了时域离散信号在频域表现为周期性函数的特性。
对于一个长度为N的有限长序列,在频域表现为周期性的连续谱 X(ejω)。如果将有限长序列以N为周期进行延拓,则在频域必将表现为周期性的离散谱X(ejωs),且单个周期的频谱形状与有限长序列相同。因此,可以将X(ejωs)看成在频域对X(ejω)等间隔采样的结果。根据采样理论可知,要想采样后能够不失真地恢复原信号,采样速率必须满足一定的条件。假设时域信号的时间长度为NT,则在频域的一个周期内, 采样点数N0必须大于或等于N。
用离散角频率变量kωs代替 中连续变量ωs,且取N0=N,则有限长序列的频谱表达式为:

令以N为周期的函数 :
![]()
x(n)为序列x(n)以N为周期的延拓,则上式可以写成:
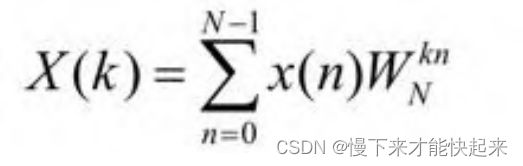
将上式的两边同乘以![]() ,可以得到:
,可以得到:

需要注意的是,上面2个式中的序列均是周期性的无限长序列。虽然是无限长序列,但只要知道该序列中一个周期的内容,序列的其他内容就知道了,所以这种无限长序列实际上只有N个序列值有信息,因此,周期序列与有限长序列有着本质的联系。
由于上面2个式中中只涉及0≤n≤N-1和0≤k≤N-1区间的值。也就是说,只涉及一个周期内的N个样本,因此,也可以用有限长序列x(n)和X(k),即各取一个周期来表示这些关系式。定义有限长序列x(n)和X(k)之间的关系为DFT,即:

2,DFT运算举例
例如,长度为4的有限长序列x1(n)=[1,1,1,1],其DFT运算过程如下:
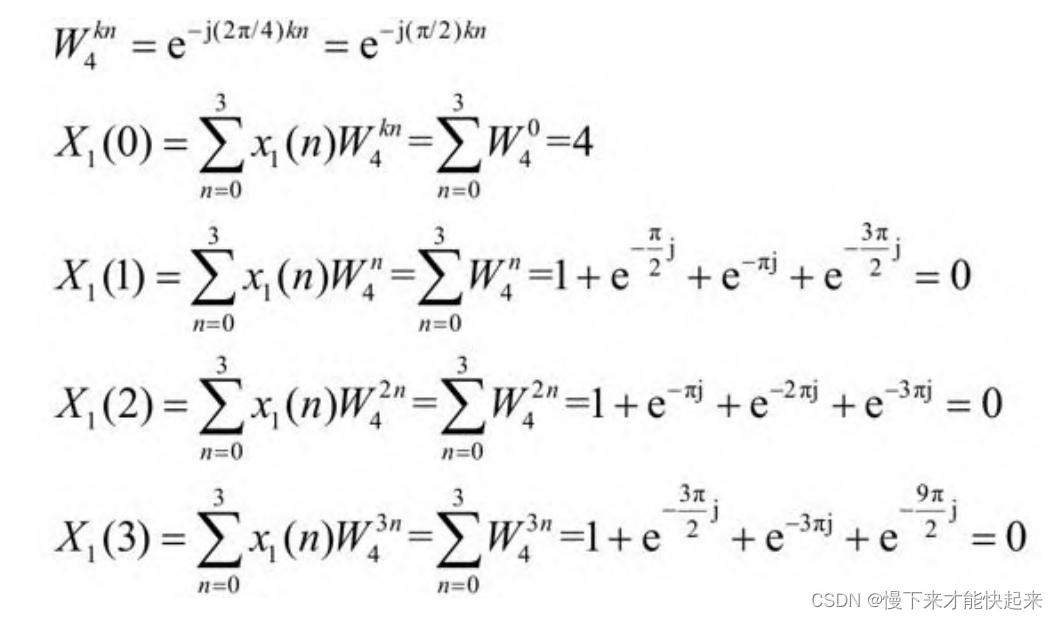
由于序列为全1,相当于对直流信号采样得到的数字信号,则仅存在零频分量(直流信号),不存在其他频率的信号,计算结果与实际情况相符。
例如,长度为4的有限长序列x2(n)=[1,2,3,4],其DFT运算过程如下:

在MATLAB中的 fft()函数可以实现序列的频域变换。可在Matlab中使用“fft([1,1,1,1])”“fft([1,2,3,4])”可得到上面两个序列的DFT结果。
3,DFT运算的常见问题
(1) 栅栏效应和序列补零
利用DFT计算频谱,只能给出频谱在ωk=2πk/N或Ωk=2πk/NT的频率分量,即频谱的采样值,而不可能得到连续的频谱函数。就好像 通过栅栏看信号频谱一样,只能在离散点上得到信号频谱,这种现象称为栅栏效应。
在DFT计算过程中,如果序列长为N个点,则只要计算N点DFT。这意味着对序列x(n)的傅里叶变换在(0,2π)区间只计算N个点的值, 其频率采样间隔为2π/N 。 如 果 序 列 长 度 较 小 , 频 率 采 样 间 隔 ωs=2π/N可能太大,会导致不能直观地说明信号的频谱特性。有一种非常简单的方法能解决这一问题,即对序列的傅里叶变换以足够小的间隔进行采样,令数字频率间隔∆ωk=2π/L,L表示是DFT的点数。显然,要提高数字频率间隔,只需要增加L即可。当序列长度N较小时, 可采用在序列后面增加L-N个零值的办法,对L点序列进行DFT,以满足所需的频率采样间隔。这样可以在保持原来频谱形状不变的情况下, 使谱线加密,即增加频域采样点数,从而可以看到原来看不到的频谱分量。
(2)频谱泄漏和混叠失真
对信号进行DFT计算,首先必须使其变成时间宽度有限的信号,方法是将序列x(n)与时间宽度有限的窗函数ω(n)相乘。例如,选用矩形窗来截断信号,在频域中相当于信号频谱与窗函数频谱的周期卷积。 卷积将造成频谱失真,且这种失真主要表现在原频谱的扩展,这种现象称为频谱泄漏。频谱泄漏会导致频谱扩展,会使信号的最高频率可 能超过采样频率的一半,从而造成混叠失真。频谱混叠 (Aliasing) 指的是在对模拟信号进行数字化采样时,由于采样频率不足,导致原本不同的频率成分在频谱中重叠在一起,造成频谱失真,难以区分不同频率成分的现象。
(3)频率分辨率与DFT参数的选择
在对信号进行DFT分析信号的频谱特征时,通常采用频率分辨率来表征在频率轴上所能得到的最小频率间隔。对于长度为N的DFT,其频率分辨率∆f=fs/N,其中fs为时域信号的采样频率,这里的数据长度N 必须是数据的有效长度。如果在x(n)中有两个频率分别为f1和f2的信 号,则在对x(n)用矩形窗截断时,要分辨这两个频率,必须满足下面的条件。
![]()
DFT时的补零没有增加序列的有效长度,所以并不能提高分辨率; 但补零可以使数据N为2的整数幂次方。补零对原X(k)起到插值作用,一方面克服栅栏效应,平滑谱的外观;另一方面,由于数据截断引起的频谱泄漏,有可能在频谱中出现一些难以确认的谱峰,补零后有可能消除这种现象。
二,FFT(快速傅里叶变换)
1、FFT(快速傅里叶变换)理论简介
快速傅里叶变换(Fast Fourier Transform,FFT)并不是一种新的变换理论,而是离散傅里叶变换(Discrete Fourier Transform, DFT)的一种高效算法。
如何高效呢?简单看一下:
在DFT的运算中。通常x(n)、X(k)和 都是复数,因此 每计算一个X(k)值,必须要进行N次复数乘法和N-1次复数加法。而 X(k)共有N个值(0≤k≤N-1),所以要完成全部DFT的运算要进行N 2次 复数乘法和N(N-1)次复数加法。乘法运算比加法运算复杂,且运算时间更长,所占用的硬件资源也更多,因此可以用乘法运算量来衡量一个算法的运算量。由于复数乘法运算最终是通过实数乘 法运算来完成的,每个复数乘法运算需要4个实数乘法运算,因此完成 全部DFT运算需要进行
次实数乘法运算。所以直接进行DFT运算的计算量太大,因此极大地限制了 DFT的应用。
仔细观察DFT运算过程,会发现系数具有对称性和周期 性,即
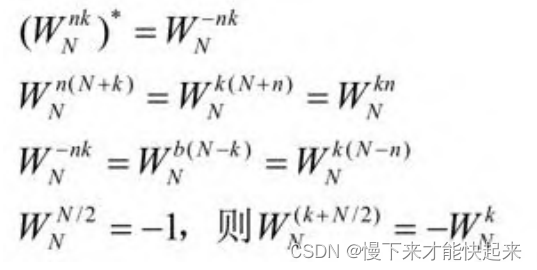
利用系数的周期性,在DFT运算中可以将某些项合并,从而减少DFT的运算量。又由于DFT的复数乘法运算次数与N2成正比,因此N越小越有利,可以利用对称性和周期性将点数大的DFT分解成多个点数小的DFT。FFT算法正是基于这样的基本思路发展起来的。
FFT算法可分为两大类:按时间抽取(Decimation-In-Time, DIT)和按频率抽取(Decimation-In-Frequency,DIF)。为了提高运算速度,将DFT运算逐次分解成点数较小的DFT运算。如果FFT算法是通过逐次分解时间序列x(n)进行的,则这种算法称为按时间抽取FFT算 法;如果FFT算法是通过逐次分解频域序列X(k)进行的,则这种算法称为按频域抽取FFT算法。
2,Xilinx FFT IP核使用详解
Vivado中IP核的配置:
(1)创建工程
打开vivado,新建工程后从IP Catalog找到FFT并双击打开;
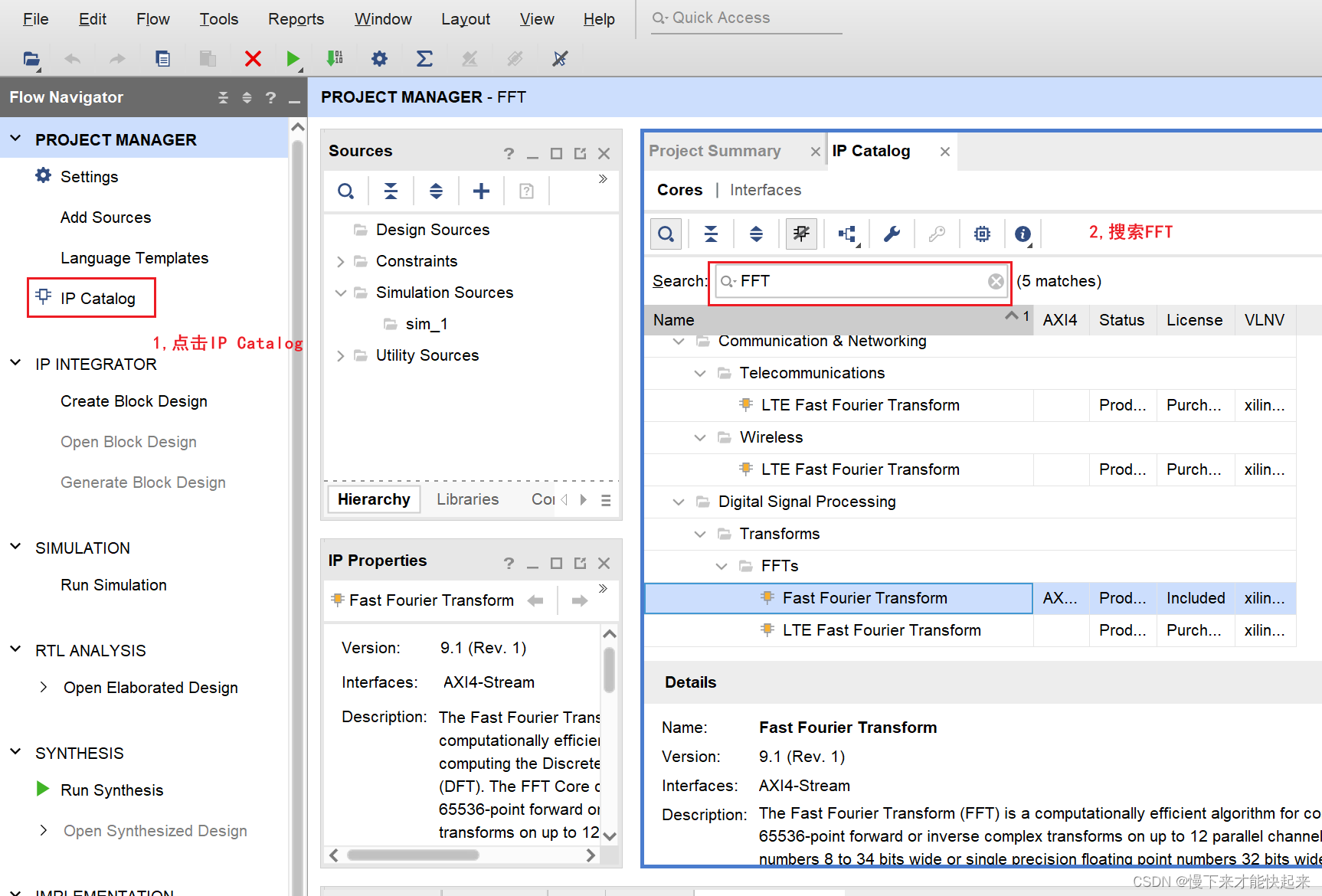
(2)第一页配置
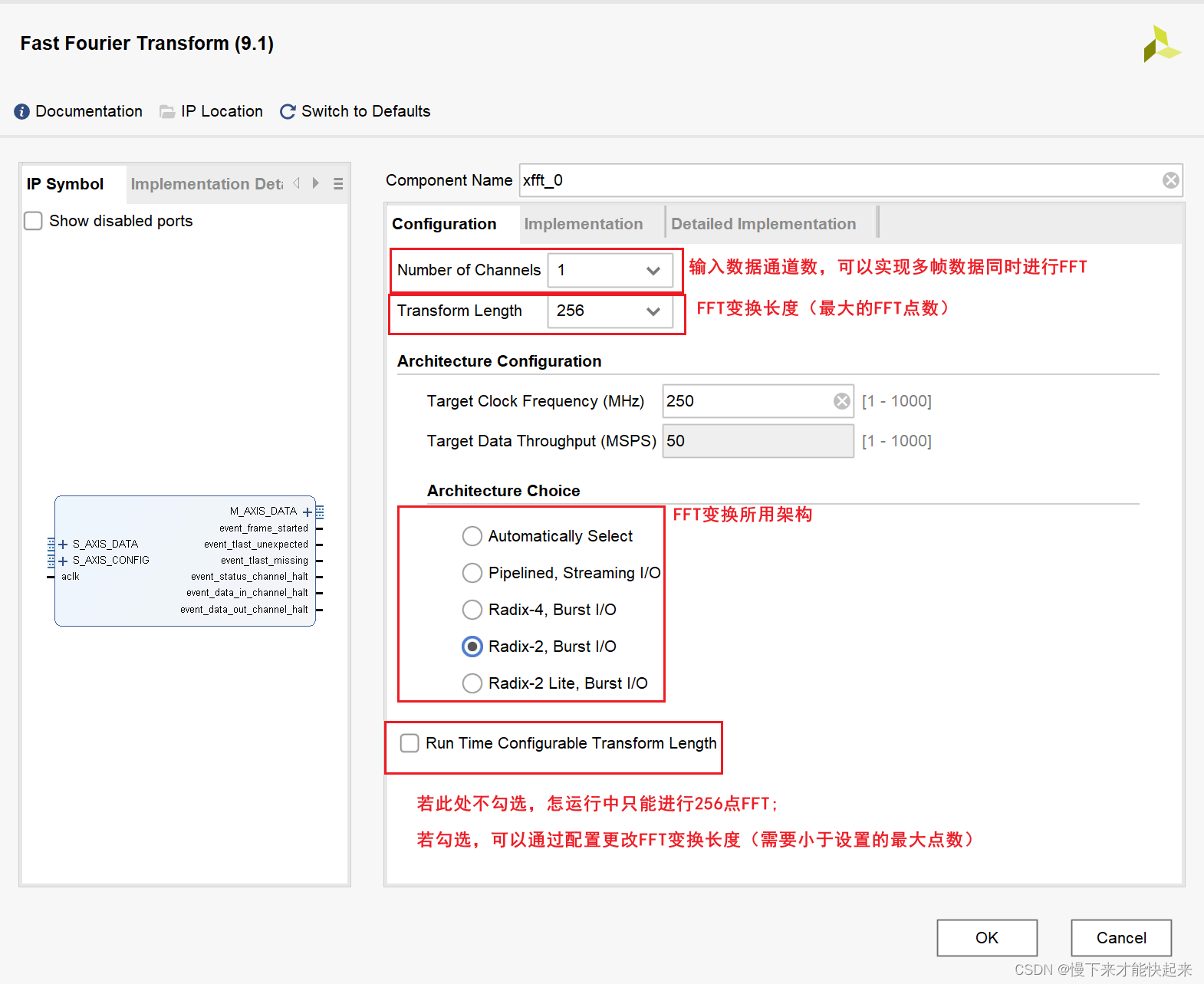
FFT核提供了4种运算结构,用户根据运算速度及硬件资源情况来选择。按运算速度从高到低(资源占用从多到少)的顺序排列,这4种运算结构分别是
- “Pipelined, Streaming I/O”
- “Radix-4, Burst I/O”
- “Radix-2, Burst I/O”
- “Radix-2 Lite, Burst I/O” 。
“Pipelined, Streaming I/O” 可 对 连 续 输 入 数 据 进 行 FFT/IFFT;
“Radix-4, Burst I/O”的数据输入和FFT/IFFT不能同时进行,也就是说,只能先输入数据,再进行FFT/IFFT,完成FFT/IFFT 后,再输入下一段数据,这种结构需要较长的时间来进行FFT/IFFT, 但只需要较少的硬件资源;
“Radix-2, Burst I/O”与“Radix-4, Burst I/O”类似,由于蝶形运算单元较少,可以在牺牲运算速度的前 提下节约硬件资源;
“Radix-2 Lite, Burst I/O”采用的蝶形运算单元比“Radix-2, Burst I/O”更少,可通过分时复用的方式进一步节 约硬件资源。
(3)第二页配置

data format:下拉标签中,对应着FFT IP核支持两种数据类型:
- 定点全精度
- 定点缩减位宽
scaling optios:缩放选项 :
- block floating point :不管输入的格式如何,FFT变化内部都采用浮点,会根据每一级的的数据情况自动缩放。 这个模式的输入输出位宽一致,便于调用。
- scaled :在m_axis_data_tuser中会有5BIT表示每一级的缩放情况,在s_axis_config_data中会有相应的字段配置配置缩放因子.每一级别包含2个stage ,2个bit 表示一级缩放,一般0-3可选,如果log(NFFT)不是2的倍数,则最高一级的缩放只能在0-1之间选取。
- unscaled :不用担心变化过程中会出现溢出,但是输入是32bit的话,输出是64bit。
Aresten: 复位信号要勾选,至少保持两个时钟的低电平。
output odering options: 输出顺序选项。
- nature order: FFT变化后的输出已经调整了顺序,按照xk_index自然顺序列出变化结果,
- bit/digital reserved oder就是按照变化后的顺序直接输出,是倒序输出,需要自己后续处理,
- cyclic perfix insertion :循环前缀插入,一般添加,在进行IFFT后可以根据s_axis_config_data中的CP长度配置自动添加CP。
optional output fileds :选项输出字段,
- xk_index:FFT 变幻的结果索引,在m_axis_data_user中有相应的字段。
- OVFLO是变换中溢出的指示信号,对应event_fft_overflow.
(4)第三页配置
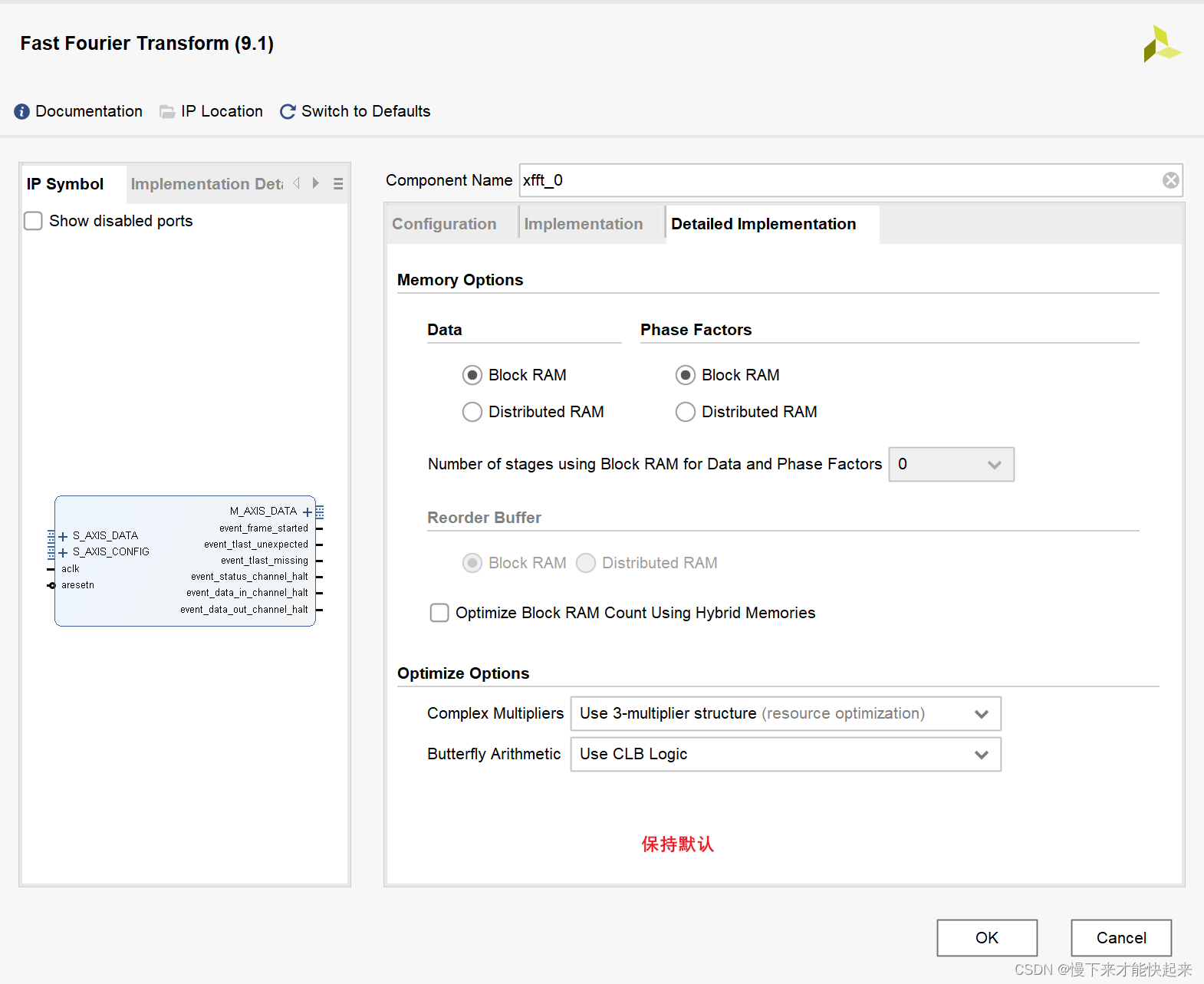
点击ok
(5)端口信号查看
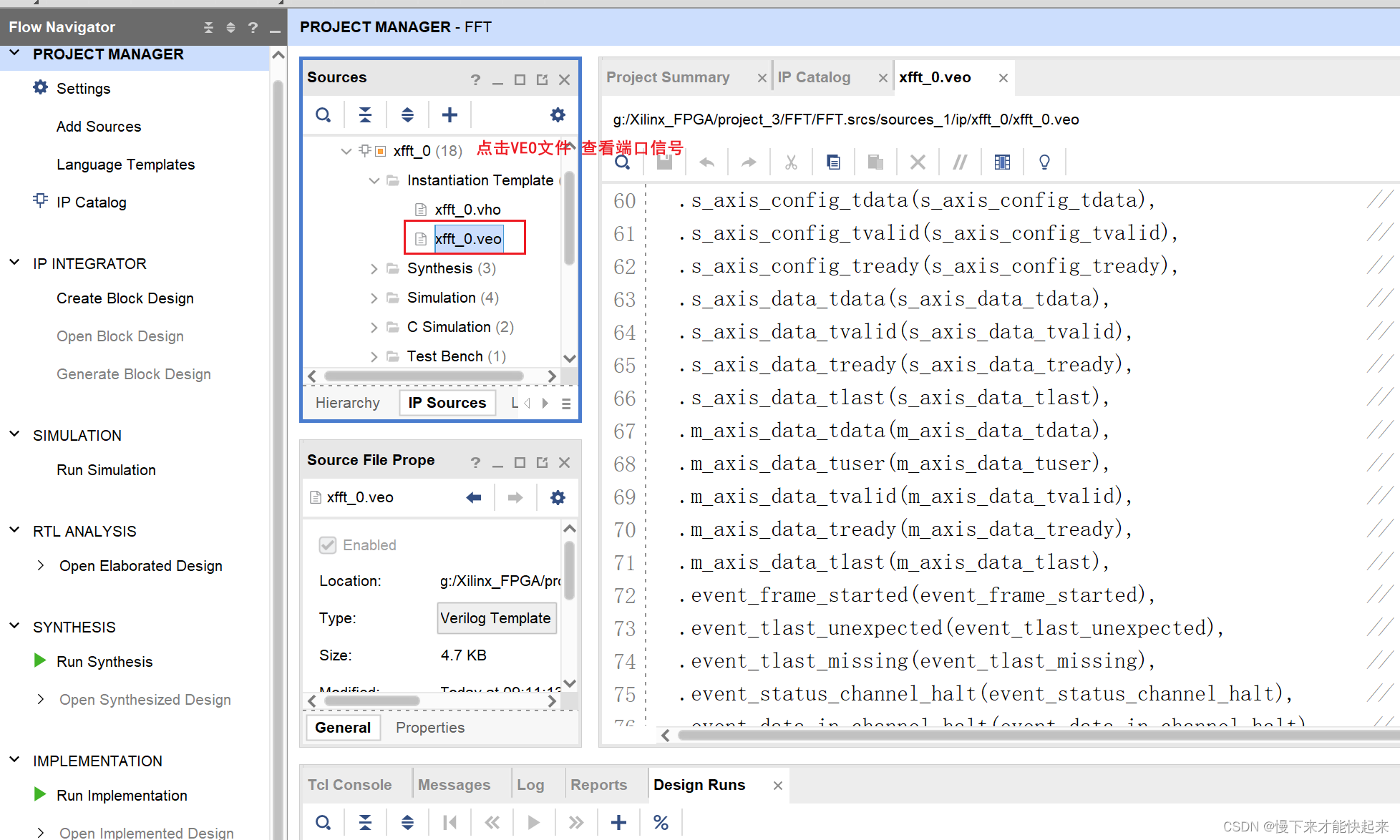

例化代码中真正对数据输入和FFT输出有关系的端口,只有s_axis_config_XXX,s_axis_data_XXX,和m_axis_data_XXX,其中前2个是输入配置,第3个是输出配置。
| s_axis_config_tdata | Input[N:0] | 控制输入模式,进行fft/ifft以及衰减因子的设置,FWD_INV = 1做 fft,FWD_INV = 0做ifft。 |
| s_axis_config_tvalid | Input | 拉高两个时钟周期之后,将端口s_axis_data_tvalid和s_axis_data_tready拉高。 |
| s_axis_config_tready | Output | s_axis_config_tvalid拉高两个时钟周期后,该口给1输出;若干个时钟周期后,自动归零。 |
| s_axis_data_tready | Output | aresetn拉高两个时钟周期后,该口给1输出;此时ip核初始化完成,可进行数据输入。 |
| s_axis_data_tvalid | Input | 当s_axis_data_tready高电平后,将s_axis_data_tvalid拉高L个周期,输入L个数据进行fft;L是FFT的点数。 |
| s_axis_data_tdata | Input[M:0] | 数据输入进行FFT运算。 |
| s_axis_data_tlast | Input | 输入L个数据后拉高,指示最后一个数据。 |
| m_axis_data_tdata | Output[M1:0] | 高位为虚部,低位为实部。 |
| m_axis_data_tvalid | Output | fft结果输出时拉高。 |
| m_axis_data_tuser | Output[M2:0] | 输出fft的地址值,输出值*fs/L为对应频点。 |
| m_axis_data_tready | Input | 保持高电平,保证FFT单元处在计算模式,并且能够输出结算结果。 |
| m_axis_data_tlast | Output | 当fft结果输出到最后一个结果时拉高,紧接着下一个时钟就拉低。 |
3,仿真测试
通过matlab对F(t) = 100 + 50cos(2pi10t) + 50cos(2pi30t) 这个信号以Fs = 100HZ进行采样,采样点数N = 256,采样完成后,将数据转换为16位二进制,并存入txt文件中。matlab程序如下:
- clear
-
- Fs=100; %采样率1ns一个点
- N = 256;
- n = 1:N;
- t = n/Fs;
- % 生成测试信号
- f1 = 10; %
- f2 = 30; %
- s1 = cos(2*pi*f1*t);
- s2 = cos(2*pi*f2*t);
- signalN = 2 + s1 + s2 ;
- data_before_fft = 50*signalN; %系数放大50倍
-
-
- fp = fopen('G:\Xilinx_FPGA\matlab\data_before_fft.txt','w');
- for i = 1:N
- if(data_before_fft(i)>=0)
- temp= dec2bin(data_before_fft(i),16);
- else
- temp= dec2bin(data_before_fft(i)+2^16+1, 16);
- end
- for j=1:16
- fprintf(fp,'%s',temp(j));
- end
- fprintf(fp,'\r\n');
- end
- fclose(fp);
-
- y = fft(data_before_fft,N);
- y = abs(y);
- f = n*Fs/N;
- plot(f,y);
-

得到采样数据,在vivado中新建测试文件:
TB文件如下:
- // -----------------------------------------------------------------------------
- // Author : LGR
- // File : TB_FFT.v
- // Create : 2024-06-25 10:01:24
- // Revise : 2024-06-25 10:17:30
- // Editor : sublime text3, tab size (4)
- // -----------------------------------------------------------------------------
- `timescale 1ns / 1ps
- module TB_FFT();
-
- reg clk ;
- reg rst_n ;
- reg signed [15:0] Time_data_I[255:0] ;
- reg data_finish_flag ;
-
- wire fft_s_config_tready ;
-
- reg signed [31:0] fft_s_data_tdata ;
- reg fft_s_data_tvalid ;
- wire fft_s_data_tready ;
- reg fft_s_data_tlast ;
-
- wire signed [63:0] fft_m_data_tdata ;
- wire signed [7:0] fft_m_data_tuser ;
- wire fft_m_data_tvalid ;
- reg fft_m_data_tready ;
- wire fft_m_data_tlast ;
-
- wire fft_event_frame_started ;
- wire fft_event_tlast_unexpected ;
- wire fft_event_tlast_missing ;
- wire fft_event_status_channel_halt ;
- wire fft_event_data_in_channel_halt ;
- wire fft_event_data_out_channel_halt ;
-
- reg [7:0] count ;
-
- reg signed [25:0] fft_i_out ;
- reg signed [25:0] fft_q_out ;
- reg signed [49:0] fft_abs ;
-
-
- initial begin
- clk = 1'b1;
- rst_n = 1'b0;
- fft_m_data_tready = 1'b1;
- $readmemb("G:/Xilinx_FPGA/matlab/data_before_fft.txt",Time_data_I);
- end
- always #5 clk = ~clk;
- always @ (posedge clk or negedge rst_n) begin
- if(!rst_n) begin
- fft_s_data_tvalid <= 1'b0;
- fft_s_data_tdata <= 32'd0;
- fft_s_data_tlast <= 1'b0;
- data_finish_flag <= 1'b0;
- count <= 8'd0;
- rst_n = 1'b1;
- end
- else if (fft_s_data_tready) begin
- if(count == 8'd255) begin
- fft_s_data_tvalid <= 1'b1;
- fft_s_data_tlast <= 1'b1;
- fft_s_data_tdata <= {Time_data_I[count],16'd0};
- count <= 8'd0;
- data_finish_flag <= 1'b1;
- end
- else begin
- fft_s_data_tvalid <= 1'b1;
- fft_s_data_tlast <= 1'b0;
- fft_s_data_tdata <= {Time_data_I[count],16'd0};
- count <= count + 1'b1;
- end
- end
- else begin
- fft_s_data_tvalid <= 1'b0;
- fft_s_data_tlast <= 1'b0;
- fft_s_data_tdata <= fft_s_data_tdata;
- count <= count;
- end
- end
- always @ (posedge clk) begin
- if(fft_m_data_tvalid) begin
- fft_i_out <= fft_m_data_tdata[24:0];
- fft_q_out <= fft_m_data_tdata[56:32];
- end
- end
- always @ (posedge clk) begin
- fft_abs <= $signed(fft_i_out)* $signed(fft_i_out)+ $signed(fft_q_out)* $signed(fft_q_out);
- end
- //fft ip核例化
- xfft_0 u_fft(
- .aclk(clk), // 时钟信号(input)
- .aresetn(rst_n), // 复位信号,低有效(input)
- .s_axis_config_tdata(8'd1), // ip核设置参数内容,为1时做FFT运算,为0时做IFFT运算(input)
- .s_axis_config_tvalid(1'b1), // ip核配置输入有效,可直接设置为1(input)
- .s_axis_config_tready(fft_s_config_tready), // output wire s_axis_config_tready
- //作为接收时域数据时是从设备
- .s_axis_data_tdata(fft_s_data_tdata), // 把时域信号往FFT IP核传输的数据通道,[31:16]为虚部,[15:0]为实部(input,主->从)
- .s_axis_data_tvalid(fft_s_data_tvalid), // 表示主设备正在驱动一个有效的传输(input,主->从)
- .s_axis_data_tready(fft_s_data_tready), // 表示从设备已经准备好接收一次数据传输(output,从->主),当tvalid和tready同时为高时,启动数据传输
- .s_axis_data_tlast(fft_s_data_tlast), // 主设备向从设备发送传输结束信号(input,主->从,拉高为结束)
- //作为发送频谱数据时是主设备
- .m_axis_data_tdata(fft_m_data_tdata), // FFT输出的频谱数据,[47:24]对应的是虚部数据,[23:0]对应的是实部数据(output,主->从)。
- .m_axis_data_tuser(fft_m_data_tuser), // 输出频谱的索引(output,主->从),该值*fs/N即为对应频点;
- .m_axis_data_tvalid(fft_m_data_tvalid), // 表示主设备正在驱动一个有效的传输(output,主->从)
- .m_axis_data_tready(fft_m_data_tready), // 表示从设备已经准备好接收一次数据传输(input,从->主),当tvalid和tready同时为高时,启动数据传输
- .m_axis_data_tlast(fft_m_data_tlast), // 主设备向从设备发送传输结束信号(output,主->从,拉高为结束)
- //其他输出数据
- .event_frame_started(fft_event_frame_started), // output wire event_frame_started
- .event_tlast_unexpected(fft_event_tlast_unexpected), // output wire event_tlast_unexpected
- .event_tlast_missing(fft_event_tlast_missing), // output wire event_tlast_missing
- .event_status_channel_halt(fft_event_status_channel_halt), // output wire event_status_channel_halt
- .event_data_in_channel_halt(fft_event_data_in_channel_halt), // output wire event_data_in_channel_halt
- .event_data_out_channel_halt(fft_event_data_out_channel_halt) // output wire event_data_out_channel_halt
- );
-
- endmodule


首先fft_s_data_tready 拉高,表示IP核准备好接受数据,然后在下一个时钟将fft_s_data_tvaild拉高。准备向IP核写入数据,count开始计数。

在 fft_s_data_tvaild有效期间,读出txt文件的数据,按顺序写入到fft_s_data_tdata中,当count计数到255,即最后一个数据时,将fft_s_data_tlast信号拉高,代表数据写入完成。
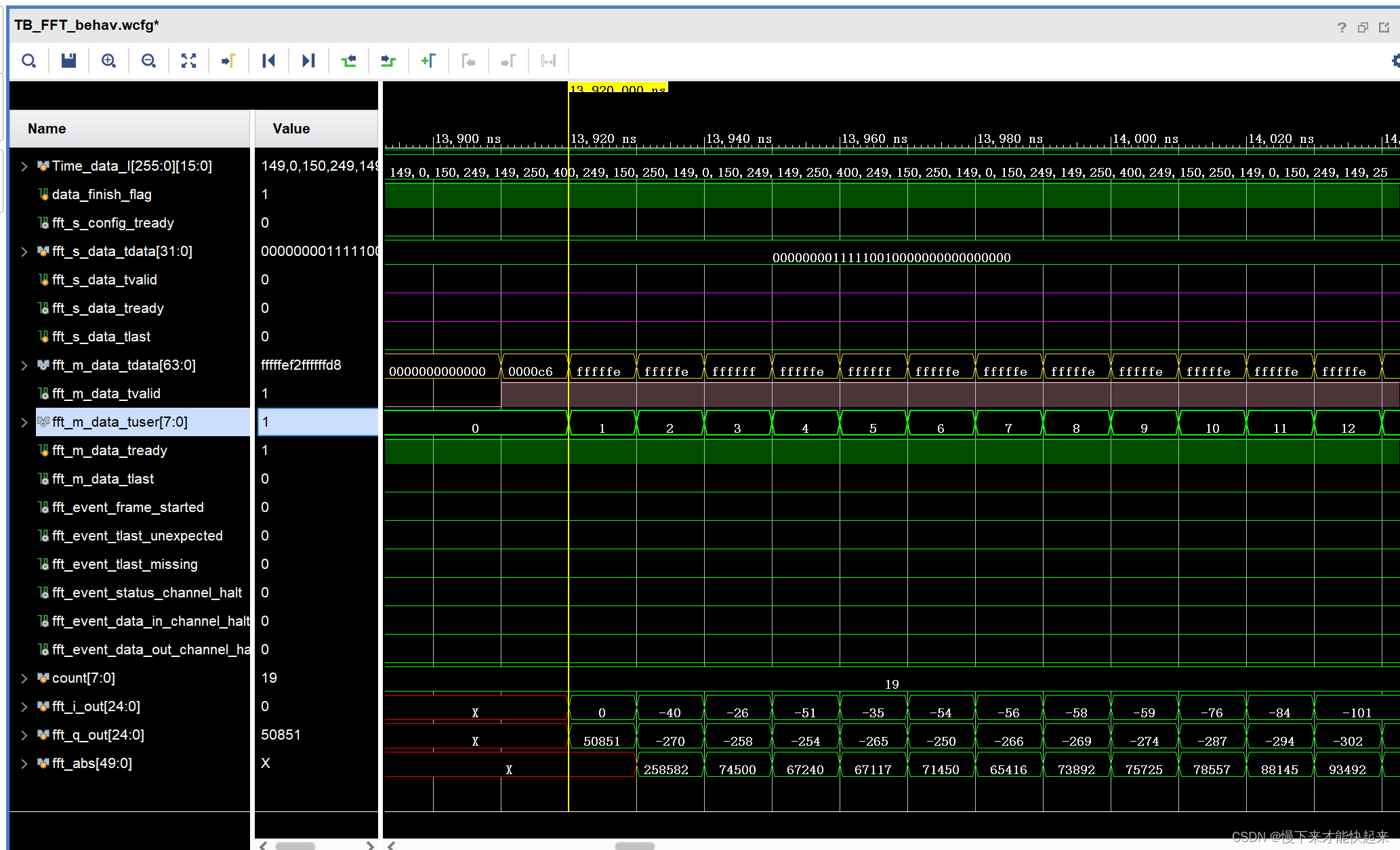
 fft_m_data_tvalid变为高电平,代表fft_m_data_tdata中将输出有效数据,即256点FFT的计算结果。
fft_m_data_tvalid变为高电平,代表fft_m_data_tdata中将输出有效数据,即256点FFT的计算结果。
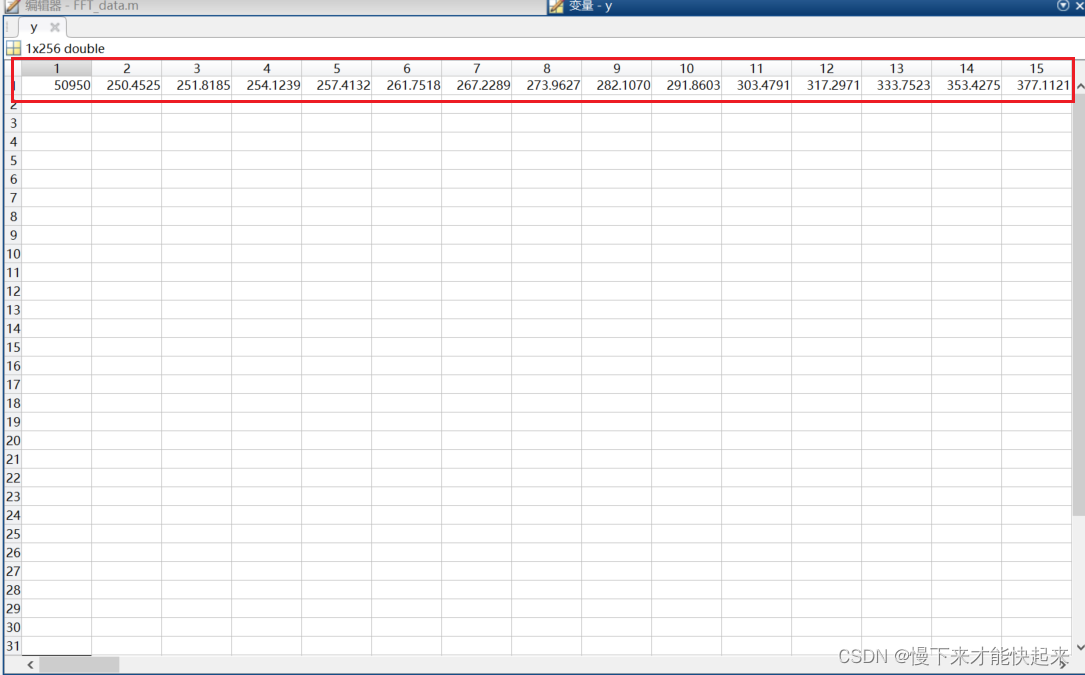
将IP核的计算结果与matlab的计算结果相对比,发现数据略有偏差。
三,总结
以上从原理介绍了DFT(离散傅里叶变换原理),然后再介绍了FFT(快速傅里叶变换)以及IP核的使用,和IP核使用参数以及配置。
参考文献:
[1]朱永前,李霄.在FPGA上实现FFT的高效串行流水线结构[J].火控雷达技术,2023,52(02):61-65.DOI:10.19472/j.cnki.1008-8652.2023.02.010.
[2]侯晓晨,孟骁,陈昊.基于FPGA的混合基FFT算法设计与实现[J].太赫兹科学与电子信息学报,2021,19(02):303-307.
[3]杜勇.Xilinx FPGA 数字信号处理设计[M].电子工业出版社:202003.339.
[4]https://blog.csdn.net/weixin_41594632/article/details/112689545
[5]尹艳清,杨湘杰,李必超,等.基于FPGA的快速傅立叶变换算法的实现[J].电子技术与软件工程,2021,(06):84-85.


