数据挖掘-08-基于Python实现时间序列分析建模(ARIMA 模型）（包括数据和代码）_arima模型应用

0. 数据代码下载

关注公众号：『AI学习星球』
回复：实现时间序列分析建模 即可获取数据下载。
算法学习、4对1辅导、论文辅导或核心期刊可以通过公众号或CSDN滴滴我

---

1. 背景描述

当今世界正处于一个数据信息时代，随着后续互联网的发展各行各业都会产 生越来越多的数据，包括不限于商店、超市、便利店、餐厅等等。那么这里面很 多数据都是随着时间产生的，这就形成了时间序列数据，而且很多时间序列数据都是非平稳时间序列数据。目前对非平稳时间序列分析应用最多的模型就是ARIMA 模型.

2. 预测目的

本项目也是通过 Python 程序来进行数据探索性分析、数据预处理、

构建 ARIMA 时序模型以及如何把模型预测的结果应用于日常的实际生活当中。

3. 数据总览

本次建模数据来源于某公司餐厅销售数据，其主要的数据基本统计概况如下：

数据项：2 项(日期、销量)，如下图所示

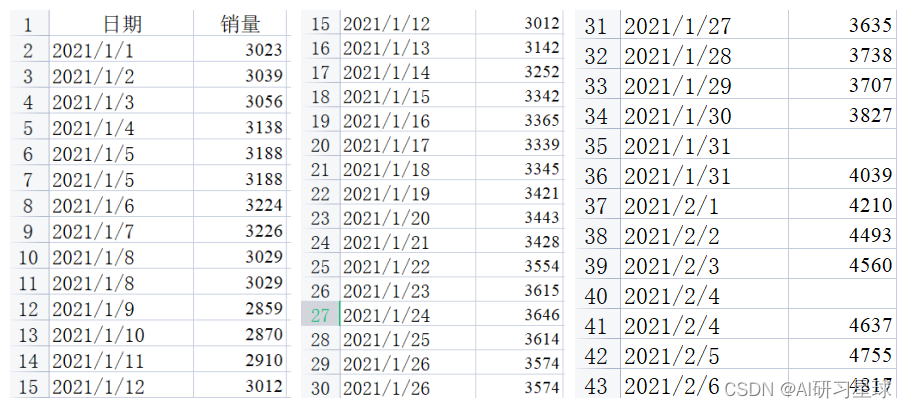
通过观察数据，发现一些空值和一些重复数据，后续章节进行处理。

4. 数据预处理

真实数据中可能包含了大量的缺失值和噪音数据或人工录入错误导致有异常点存在，非常不利于算法模型的训练。数据清洗的结果是对各种脏数据进行对应方式的处理，得到标准的，干净的、连续的数据，提供给数据统计、数据挖掘等使用。数据预处理通常包含数据
清洗、归约、聚合、转换、抽样等方式，数据预处理质量决定了后续数据分析挖掘及建模
工作的精度和泛化价值。

4.1数据描述性统计与清洗

a. 导入程序库

将所用到的程序库导入到 Python 程序中，如图所示。

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.stattools import adfuller as ADF
from statsmodels.graphics.tsaplots import plot_pacf
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.tsa.arima_model import ARIMA
1
2
3
4
5
6
7

b. 读取数据

使用 Pandas 库中 read_excel 方法读取 Excel 数据，并转为DataFrame 类型。

读取数据代码如图所示：

# 读取数据，指定日期列为指标，pandas自动将“日期”列识别为Datetime格式
data = pd.read_excel(discfile)
1
2

c. 查看统计信息和空值

print(data.describe())
print(data.info())
1
2

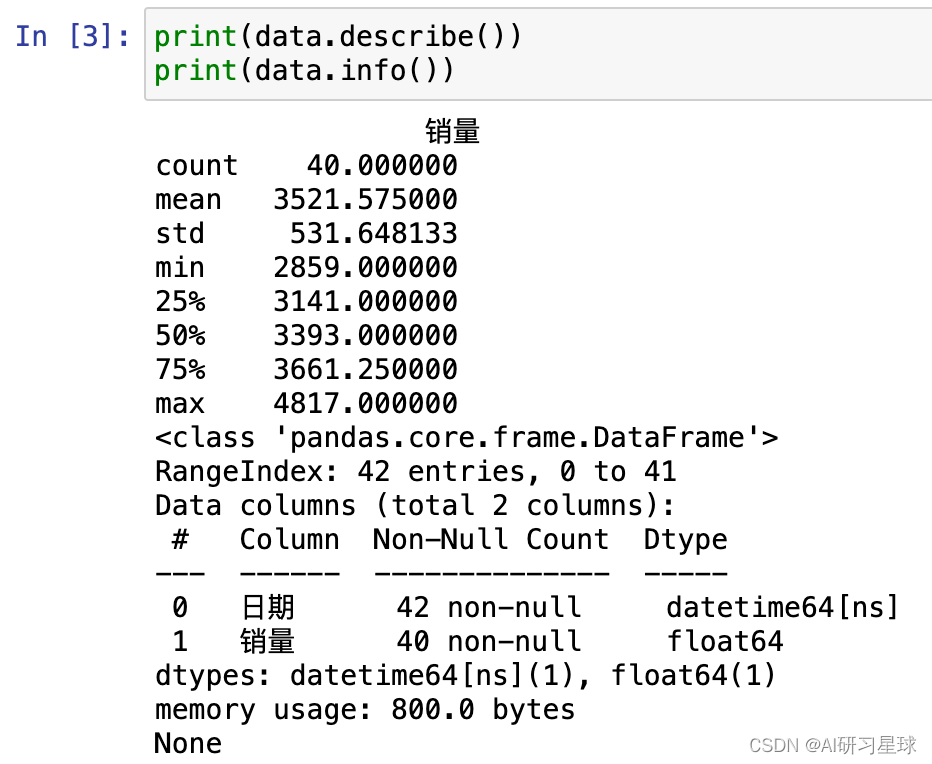
从上图可以看到，数据总数据量 40 条(不包括空值)，以及未去除重复值的平均

值、标准差、最小值、最大值、分位数。另外可以看到销量有 2 条空值。

d. 查看是否有重复数据以及清理重复数据

print(data.duplicated(subset=['日期', '销量']))
data = data.drop_duplicates(subset=['日期', '销量'], keep='first')
1
2

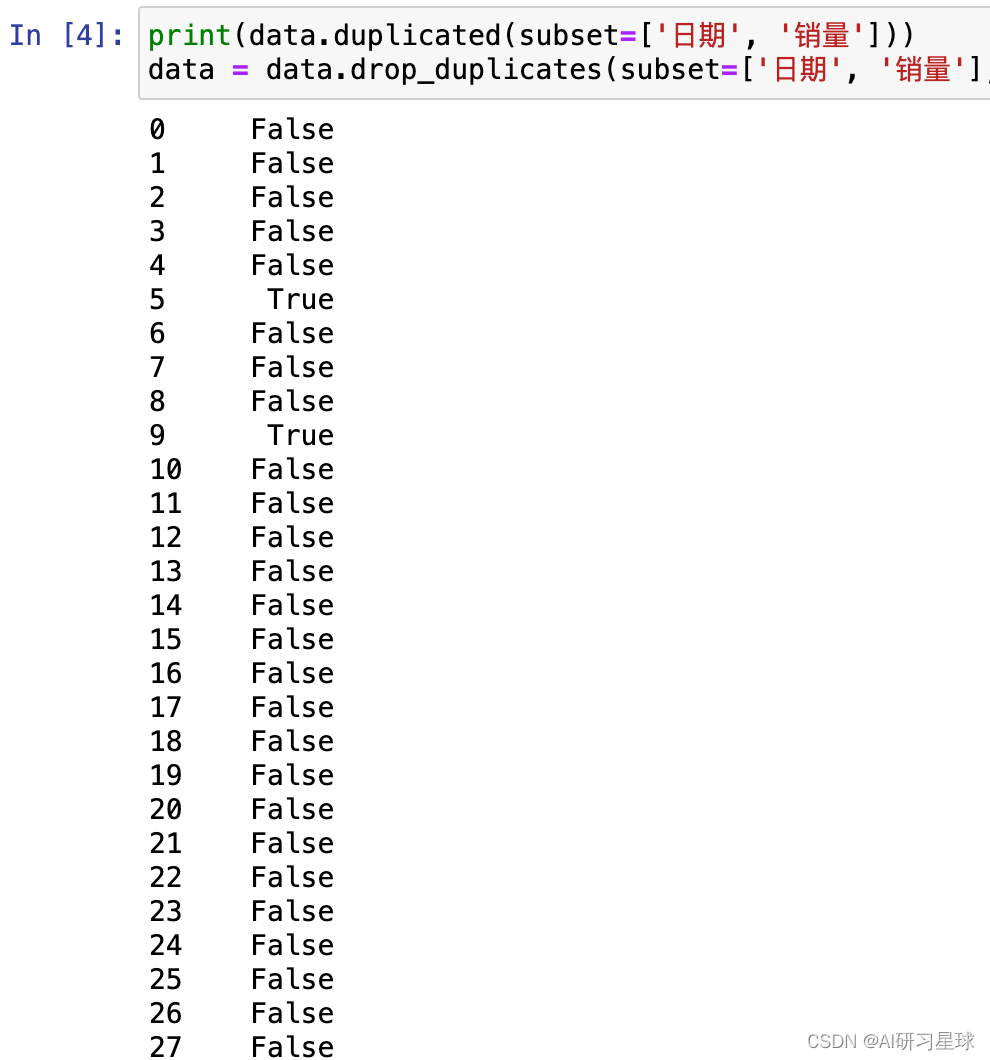
从上图中的部分展示，可以看到是有重复数据，所以使用 drop_duplicates()函
数进行了重复数据清理。

e. 空值清理

本项目涉及 2 条空值数据 直接进行丢弃操作。
空值的处理也可以用均值填充、分位数填充、拉格朗日插值填充等等(根据具体数据处理的需要进行即可)。

data = data.dropna()
1

f. 针对清洗后的数据进行统计分析

print(data.describe())
print(data.info())
1
2

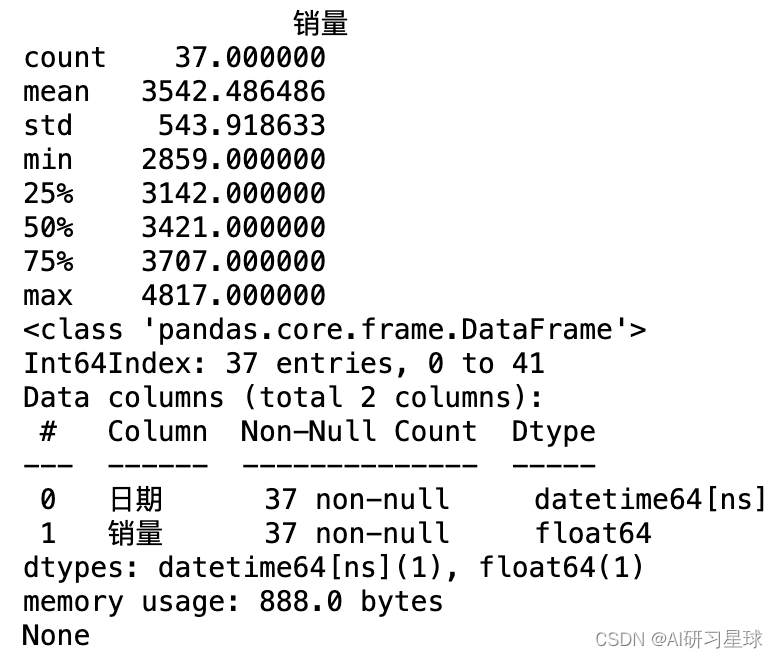
从上图可以看出，清洗后数据量为 37 条，平均值为 3542.49、标准差为 543.92。

5. 探索性数据分析

5.1 数据分析

销量时间序列分析：

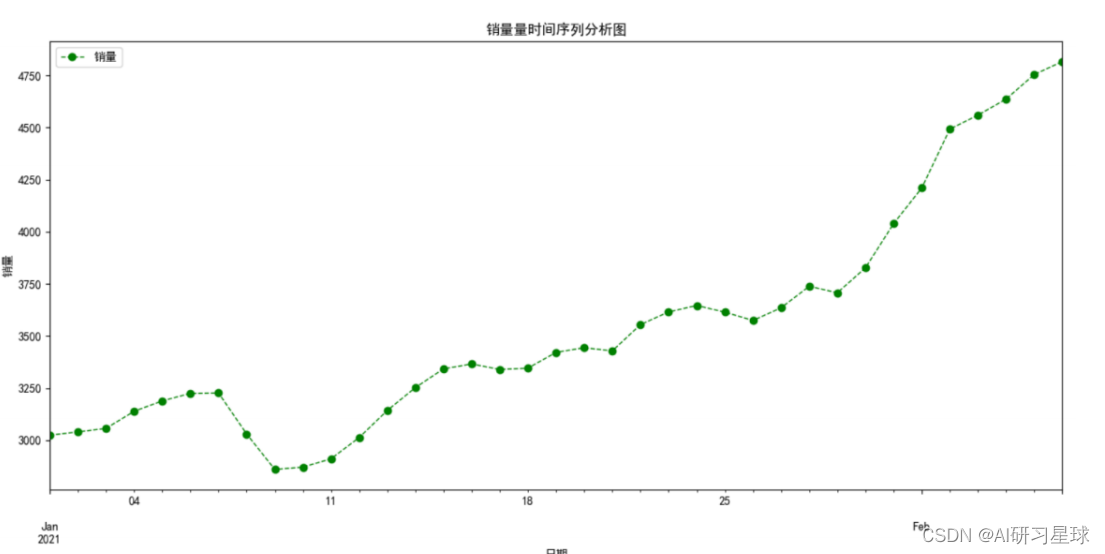
关键代码如下：

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
data.plot(color='green', marker='o', linestyle='dashed', linewidth=1, markersize=6)
plt.ylabel('销量')
plt.title("销量量时间序列分析图")
1
2
3
4
5

6. 构建 ARIMA 时序模型

6.1 ARIMA 模型概念

在自然界中绝大部分序列都是非平稳的。因而非平稳时间序列的分析更普遍、更重要，创造出来的分析方法也更多。

非平稳时间序列的分析方法可以分为确定性因素分解的时序分析和随机时序分析两大类。

• 确定性因素分解的方法把所有序列的变化都归结为 4 个因素（长期趋势、季节变动、循环变动和随机波动）的综合影响，其中长期趋势和季节变动的规律性信息通常比较容易提取，而由随机因素导致的波动则非常难以确定和分析，对随机信息浪费严重会导致模型拟合精度不够理想。

• 随机时序分析法的发展就是为了弥补确定性因素分解方法的不足。根据时间

序列的不同特点，随机时序分析可以建立的模型有 ARIMA 模型、残差自回归模型、季节模型、异方差模型等。

本项目重点介绍 ARIMA 模型对非平稳时间序列进行建模。

差分运算：

1. p 阶差分
   相距一期的两个序列值之间的减法运算称为 1 阶差分运算。

2. k 步差分
   相距 k 期的两个序列值之间的减法运算称为 k 步差分运算。差分运算具有强大的确定性信息提取能力，许多非平稳序列差分后会显示出平稳序列的性质，这时称这个非平稳序列为差分平稳序列。差分平稳序列可以使用 ARMA 模型进行拟合。ARIMA 模型的实质就是差分运算与 ARMA 模型的组合。

6.2 序列平稳性检验

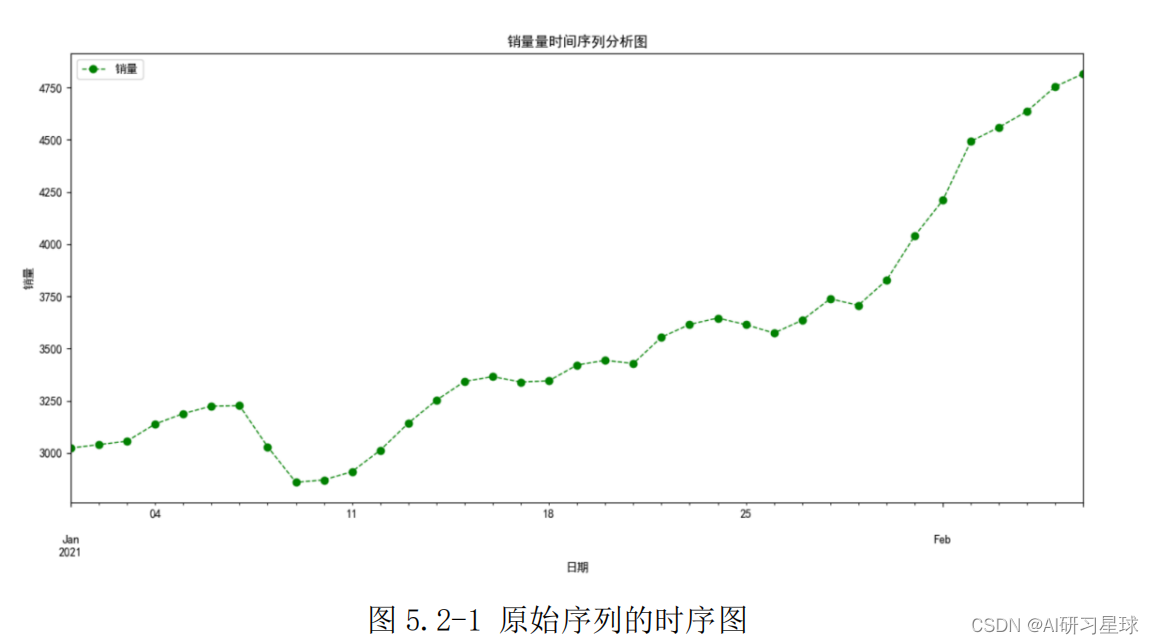
此图显示该序列具有明显的单调递增趋势，可以判断为非平稳序列。

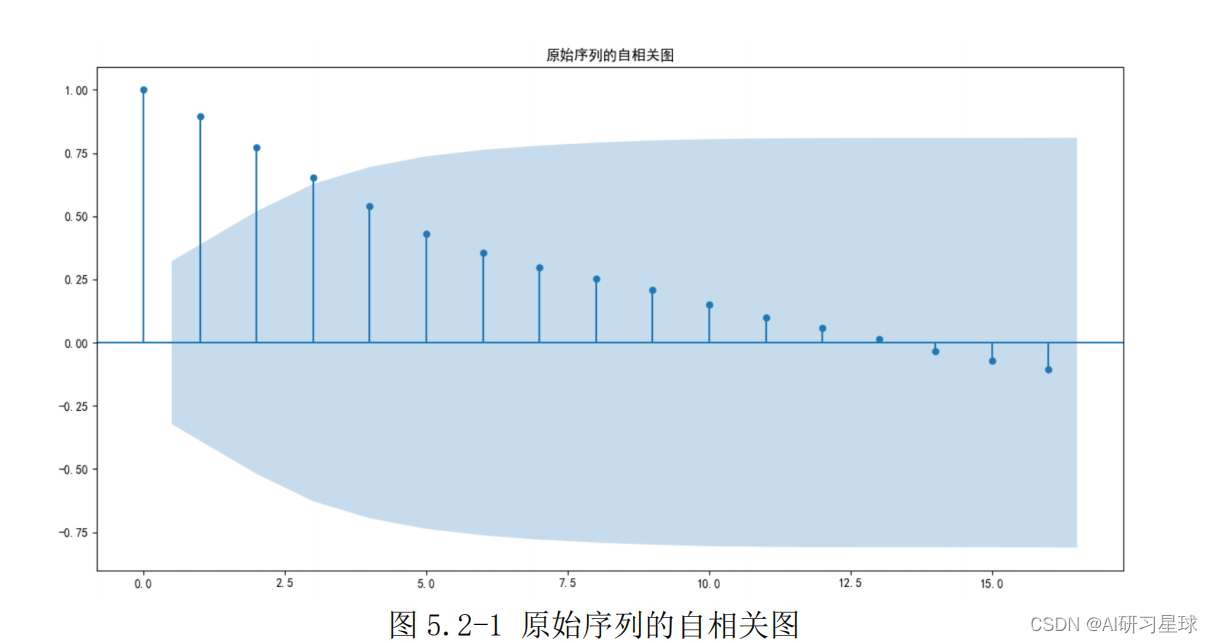
此图的自相关图显示自相关系数长期大于零，说明序列间具有很强的长期相关性。

此表单位根检验统计量对应的 p 值显著大于 0.05，最终将该序列判断为非平稳序列（非平稳序列一定不是白噪声序列）。

6.3 对原始序列进行一阶差分，并进行平稳性和白噪声检验

a. 对一阶差分后的序列再次做平稳性判断。

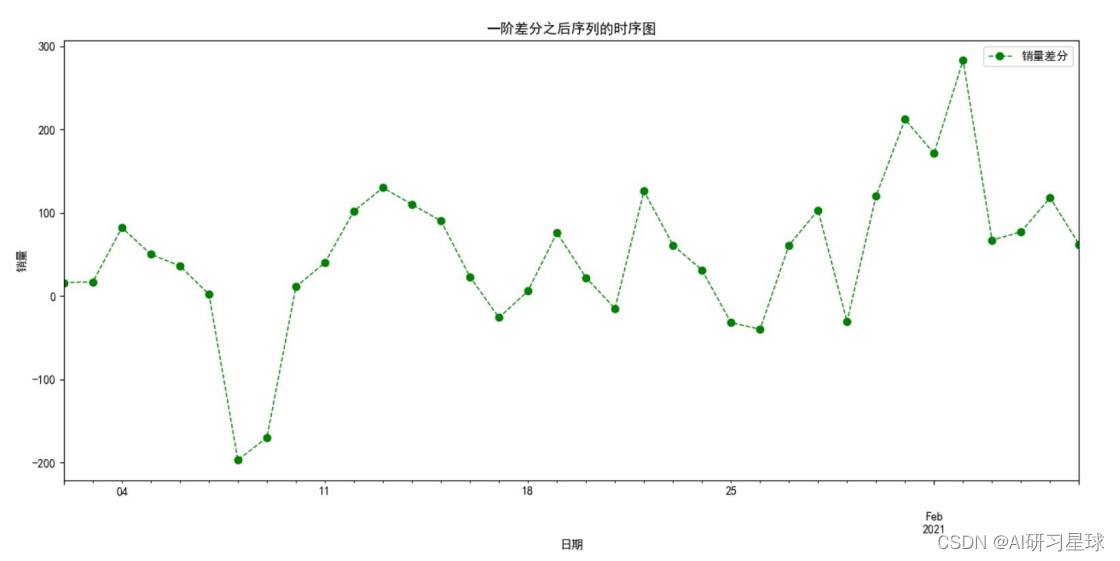
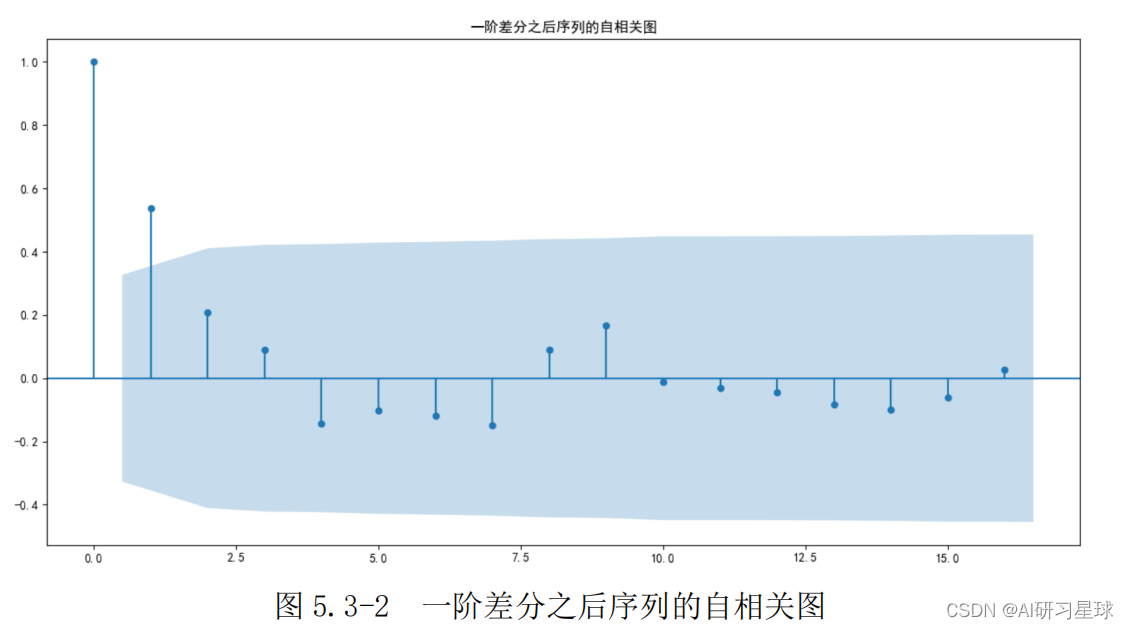
结果显示，一阶差分之后序列的时序图在均值附近比较平稳地波动、自相关图有很强的短期相关性、单位根检验 p 值小于 0.05，所以一阶差分之后的序列是平稳序列。

b. 对一阶差分后的序列做白噪声检验

此表输出的 p 值远小于 0.05，所以一阶差分之后的序列是平稳非白噪声序列.

6.4 对一阶差分后的序列拟合 ARMA 模型

下面进行模型定阶。模型定阶就是确定 p 和 q。

第一种方法：人为识别

根据图 5-25 进行模型定阶。

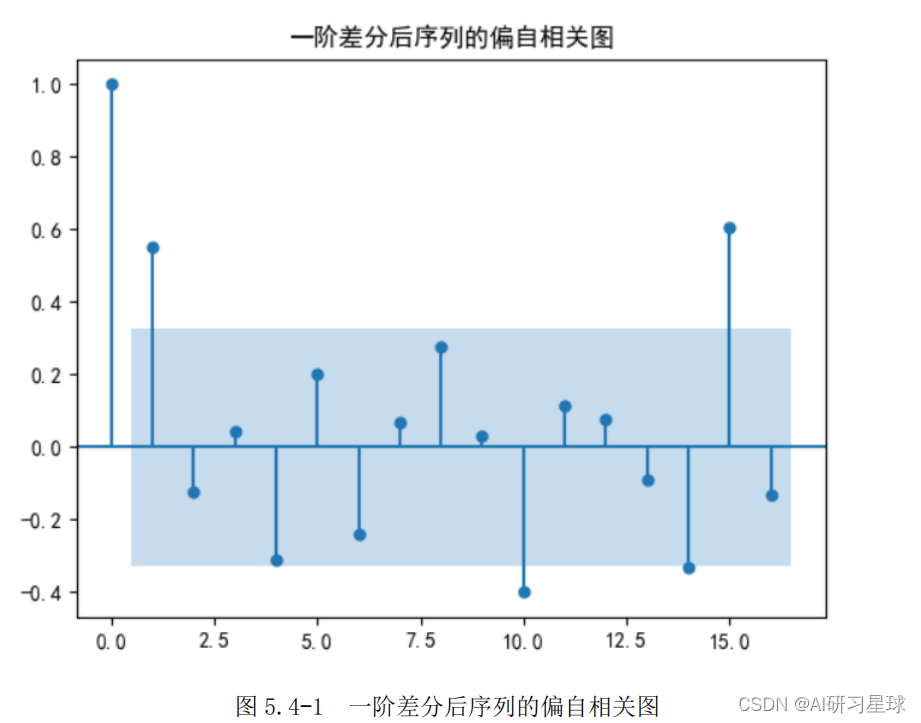
一阶差分后自相关图显示出 1 阶截尾，偏自相关图显示出拖尾性，所以可以考虑用 MA(1)模型拟合 1 阶差分后的序列，即对原始序列建立 ARIMA(0，1，1)模型。

第二种方法：相对最优模型识别。

计算 ARMA(p，q) 当 p 和 q 均小于等于 3 的所有组合的 BIC 信息量，取其中BIC 信息量达到最小的模型阶数。

计算完成 BIC 矩阵如下：

当 p 值为 0、q 值为 1 时，最小 BIC 值为 422.510082。p、q 定阶完成。

用 AR(1)模型拟合一阶差分后的序列，即对原始序列建立 ARIMA(0，1，1)模型。虽然两种方法建立的模型是一样的，但模型是非唯一的。ARIMA(1，1，0)和ARIMA(1，1，1)这两个模型也能通过检验。下面对一阶差分后的序列拟合 AR(1)

模型进行分析:
1）参数检验和参数估计见下表:

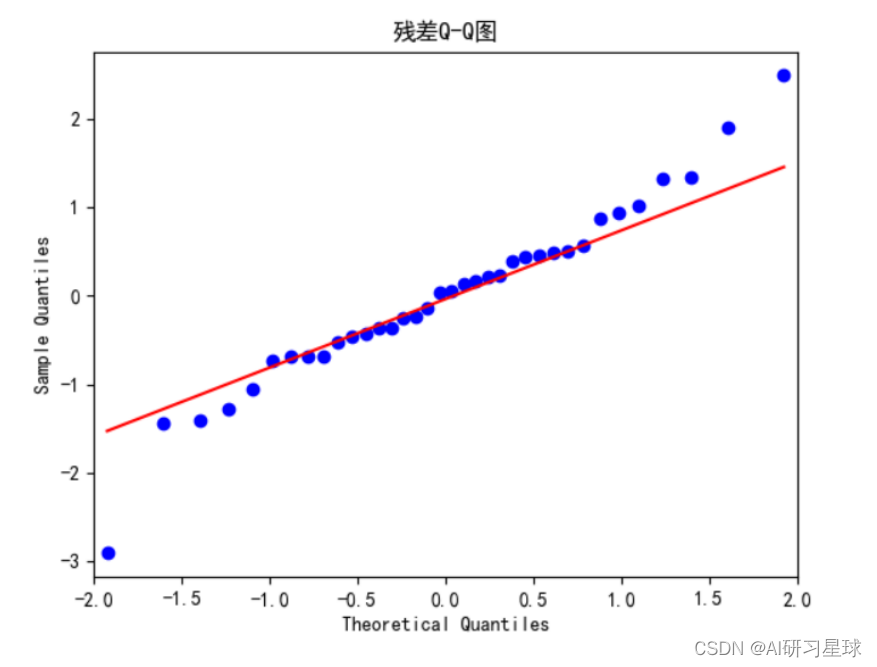
2）模型检验之残差检验：



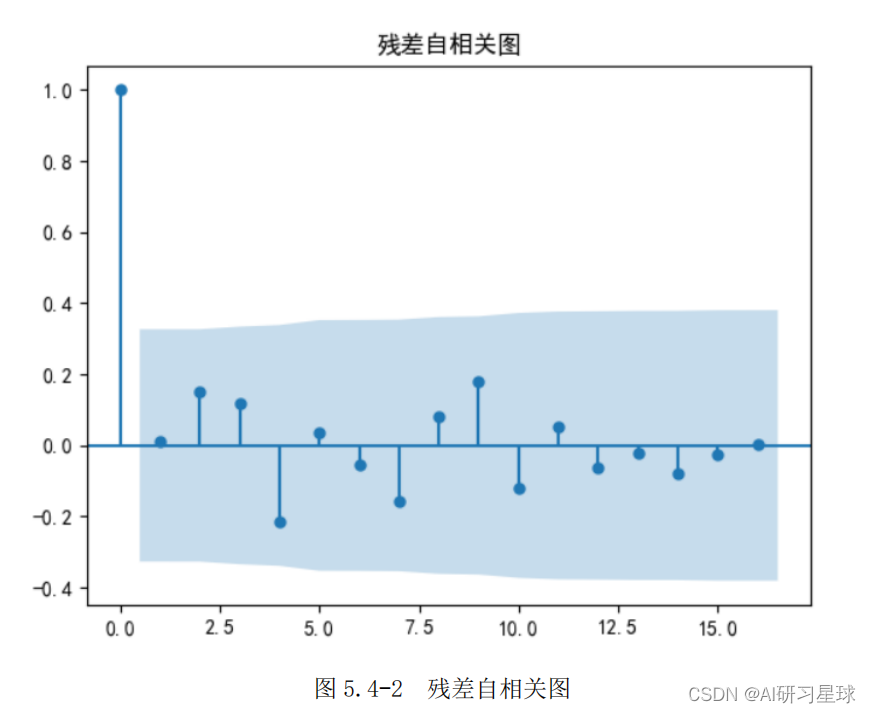
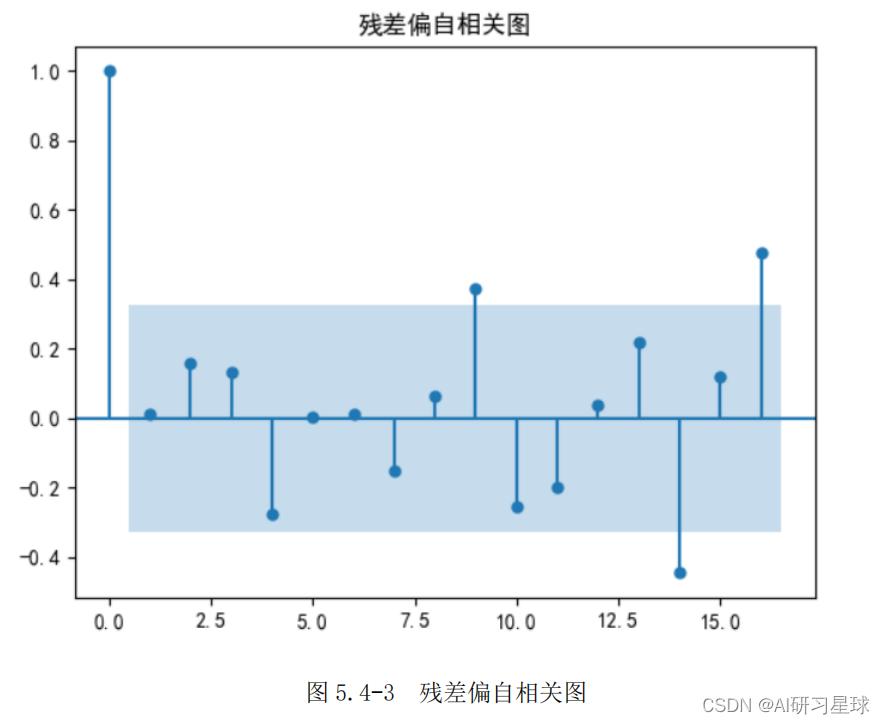
D-W 检验：

• DW 值显著的接近于 0 或４时，则存在自相关性，而接近于２时，则不存在（一阶）自相关性。
• D-W 检验的结果为：1.9735。因此，模型预测的残差不存在自相关性性，这说明拟合的模型预测效果很好。
• 残差序列的白噪声检验结 果为： (array([0.00390439]), array([0.95017654]))，可以看出 p 值为 0.9502， P>0.05.说明原假设成立。

6.5 ARIMA 模型预测

应用 ARIMA(0，1，1)对表某餐厅的销售数据做为期 5 天的预测，结果如下表所示：

需要说明的是，利用模型向前预测的时期越长，预测误差将会越大，这是时间预测的典型特点。
代码如下

# 参数初始化
discfile = 'data.xlsx'
forecastnum = 5

# 读取数据，指定日期列为指标，pandas自动将“日期”列识别为Datetime格式
data = pd.read_excel(discfile)
print(data.describe())
print(data.info())

print(data.duplicated(subset=['日期', '销量']))
data = data.drop_duplicates(subset=['日期', '销量'], keep='first')
data = data.dropna()
print(data.describe())
print(data.info())
data = data.set_index('日期')
print(data.head())

# 时序图

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
data.plot(color='green', marker='o', linestyle='dashed', linewidth=1, markersize=6)
plt.ylabel('销量')
plt.title("销量量时间序列分析图")
plt.show()

# 自相关图

plot_acf(data)
plt.title("原始序列的自相关图")
plt.show()

# 平稳性检测

print(u'原始序列的ADF检验结果为：', ADF(data[u'销量']))
# 返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore

# 差分后的结果
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
D_data.plot(color='green', marker='o', linestyle='dashed', linewidth=1, markersize=6)  # 时序图
plt.title("一阶差分之后序列的时序图")
plt.ylabel('销量')
plt.show()
plot_acf(D_data)  # 自相关图
plt.title("一阶差分之后序列的自相关图")
plt.show()

print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分']))  # 平稳性检测

# 白噪声检验

print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1))  # 返回统计量和p值

plot_pacf(D_data)  # 偏自相关图
plt.title("一阶差分后序列的偏自相关图")
plt.show()

# 定阶
data[u'销量'] = data[u'销量'].astype(float)
pmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
qmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
bic_matrix = []  # BIC矩阵
for p in range(pmax + 1):
    tmp = []
    for q in range(qmax + 1):
        try:  # 存在部分报错，所以用try来跳过报错。
            tmp.append(ARIMA(data, (p, 1, q)).fit().bic)
        except:
            tmp.append(None)
    bic_matrix.append(tmp)

bic_matrix = pd.DataFrame(bic_matrix)  # 从中可以找出最小值
print('BIC矩阵：')
print(bic_matrix)

tmp_data = bic_matrix.values
tmp_data = tmp_data.flatten()
s = pd.DataFrame(tmp_data, columns=['value'])
s = s.dropna()
print('BIC最小值：', s.min())
s.to_excel('tmp.xlsx')

p, q = bic_matrix.stack().idxmin()  # 先用stack展平，然后用idxmin找出最小值位置。
print(u'BIC最小的p值和q值为：%s、%s' % (p, q))

model = ARIMA(data, (p, 1, q)).fit()  # 建立ARIMA(0, 1, 1)模型
print('模型报告为：\n', model.summary2())
print('模型报告为：\n', model.summary())
resid = model.resid
# 自相关图
plot_acf(resid)
plt.title("残差自相关图")
plt.show()
# 偏自相关图
plot_pacf(resid)
plt.title("残差偏自相关图")
plt.show()
# 线性即正态分布
qqplot(resid, line='q', fit=True)
plt.title("残差Q-Q图")
plt.show()
# 解读：残差服从正态分布，均值为零，方差为常数
print('D-W检验的结果为：', sm.stats.durbin_watson(resid.values))
print('残差序列的白噪声检验结果为：', acorr_ljungbox(resid, lags=1))  # 返回统计量、P值

print('预测未来5天，其预测结果、标准误差、置信区间如下：\n', model.forecast(5))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107

7. 实际应用

通过上面的预测结果分析得到，此模型能够在误差允许的范围内进行预测未来的销量，可以将此模型应用于实际生产中，帮助企业更好地备货。

---

0. 数据代码下载

关注公众号：『AI学习星球』
回复：实现时间序列分析建模 即可获取数据下载。
算法学习、4对1辅导、论文辅导或核心期刊可以通过公众号或CSDN滴滴我