- 1PYQT组件的应用详解
- 2素数求和问题_请进行程序设计,找出n个输入数据中的所有素数,对其进行求和运算。输入说明:输入数
- 3HarmonyOS学习,灵活运用工程结构及应用程序结构
- 4ChatGPT学习-如何向ChatGPT提问_怎么问chatgpt问题
- 5【s5p6818】fastboot驱动安装
- 6jquery——get方法解析xml文件和json文件和getjson_jquery xml get
- 7讯飞 AIUI 集成_讯飞 aiui tpp
- 8Java验证对象的属性值是否都为空_便利集合校验集合里面对象的几个属性为空
- 9LSTM网络结构_lstm隐藏层神经元个数
- 10小程序 祝福小工具源码分享_点香祈福小程序源代码
旋转位置编码RoPE总结_rope位置编码
赞
踩
旋转位置编码RoPE总结
前言
Rotary Position Embedding (RoPE)可谓是今年Transformer模型改进中的一大热门内容,在大模型时代,RoPE在LLaMA、ChatGLM、Palm中得到应用,并证明其有效性。RoPE的诞生可以追溯到2021年,由苏剑林大神在《RoFormer: Enhanced Transformer with Rotary Position Embedding》首次提出,通过一种旋转矩阵的方式构建绝对位置编码表示相对位置,有效地改善了传统位置编码不能很好地捕捉相对位置的问题,同时也为长度外推提供了可扩展性。
基础知识
位置编码
位置编码的出现追溯到2017年Transformer刚刚提出之时。不同于RNN系列网络的递归特性,后者能够根据不同时间步自动捕获序列数据的先后状态,而Transformer以Attention+FFN为基本模块,如果仅使用特征Embedding模型会将每个位置的token都平等对待,无法分辨出先后关系。拿一个简单的BERT分类任务来说,将输入句子转换为不带位置信息的tokens序列,然后做Embedding输入到网络,进过多层Attention+FFN模块后每个token都获得了其它token的相关信息,最终隐层输出后一般是len维上mean_pooling、max_pooling或直接取cls进行映射。上述整个过程模型只是获得了句子的每个token依赖上下文的内容编码,而没有融入位置信息。这就意味着如果把原句子的token序列随机打乱输入BERT后,分类结果也是一样的!这显然不合理。上述情况可以理解为“词袋式编码”。
因此Transformer系列模型的输入一般是需要加入位置特征的,这样能够确保输入序列的位置关系耦合性,而不是仅仅的词袋信息。
现有方案
绝对位置编码
Sinusoidal编码
Sinusoidal编码即基于正余弦的绝对位置编码,也是Transformer论文上提出的原生编码方式。它通过在Embedding阶段将输入向量直接与正余弦信息相加,正余弦计算公式如下:
f
(
x
,
i
)
=
W
t
(
x
+
p
i
)
,
t
∈
{
q
,
k
,
v
}
p
i
,
k
=
{
s
i
n
(
i
/
1000
0
2
t
/
d
)
k
=
2
t
c
o
s
(
i
/
1000
0
2
t
/
d
)
k
=
2
t
+
1
f(x, i) =W_t(x+ p_i),t\in \{q,k,v\} \\ p_{i,k} =
通过这种三角函数式的递进位置编码,模型能够分辨出每个token的绝对位置,也能进一步推断出token之间的相对位置。原理在于三角函数的和角公式特性:
s
i
n
(
A
+
B
)
=
s
i
n
A
⋅
c
o
s
B
+
c
o
s
A
⋅
s
i
n
B
c
o
s
(
A
+
B
)
=
c
o
s
A
⋅
c
o
s
B
−
s
i
n
A
⋅
s
i
n
B
sin(A+B) = sinA·cosB + cosA·sinB \\ cos(A+B)=cosA·cosB-sinA·sinB
sin(A+B)=sinA⋅cosB+cosA⋅sinBcos(A+B)=cosA⋅cosB−sinA⋅sinB
假设位置M、N两个token,其中N>M,二者相差P,则根据上述公式:
s
i
n
N
=
s
i
n
(
M
+
P
)
=
s
i
n
M
⋅
c
o
s
P
+
c
o
s
M
⋅
s
i
n
P
=
(
s
i
n
M
c
o
s
M
)
⋅
(
c
o
s
P
s
i
n
P
)
c
o
s
N
=
c
o
s
(
M
+
P
)
=
c
o
s
M
⋅
c
o
s
P
−
s
i
n
M
⋅
s
i
n
P
=
(
c
o
s
M
s
i
n
M
)
⋅
(
c
o
s
P
−
s
i
n
P
)
sin N= sin(M+P)\\ =sinM·cosP + cosM·sinP \\ =
对于sin变换,能够清晰地看出位置N和query的位置M之间的关系,前者相比后者的位置多P个距离,相当于多乘了
(
c
o
s
P
s
i
n
P
)
参数式编码
建立在如下假设上:位置编码也要根据向量表示去调整,而不是仅仅遵从某种分布的固定值。为此提出可训练式位置编码,将位置信息用max_length * dim的矩阵表示,同样是在Embedding阶段嵌入,但是具有梯度、可更新的。这种编码为模型提供一种可自适应的模式,但不像正余弦编码那样直观地反映相对关系,或者说这种编码方式让tokens之间几乎独立,模型很难捕获相对位置。
相对位置编码
提出动机
绝对位置编码为特征向量添加位置向量,使模型获得每个token的绝对位置信息,通过正弦的和角公式原理有效推理出相对位置关系。但存在两个问题:①虽然Sinosoidal式编码能够反映出相对位置,但在Self-Attention的q、k查询机制下性能依然有限,因为不同的m、n位置所推理的相对编码可能受m、n本身影响,需要探索一种完全不受m、n影响的更通用的编码表示;②绝对位置编码的嵌入一般发生在Embedding阶段,而现代的Transformer、BERT或GPT等结构的模型往往包含更深的网络层,仅在Embedding嵌入位置信息,随着网络的前向迭代很容易衰减甚至消失。
方案一
因而相对位置编码便产生了,相对位置编码最早可见谷歌的《Self-Attention with Relative Position Representations》工作,里面提出一种作用在Attention计算时的位置嵌入方式。首先来回顾一下Transformer中标准Attention的计算方法,公式如下:
q
i
=
x
i
⋅
W
Q
k
i
=
x
i
⋅
W
K
v
i
=
x
i
⋅
W
V
α
i
,
j
=
s
o
f
t
m
a
x
(
q
i
⋅
k
j
T
d
)
o
i
=
∑
j
α
i
,
j
⋅
v
j
q_i = x_i · W_Q \\ k_i = x_i· W_K \\ v_i = x_i · W_V \\ \alpha_{i, j} = softmax(\frac {q_i·k_j^T}{\sqrt d}) \\ o_i = \sum_j \alpha_{i,j} · v_j
qi=xi⋅WQki=xi⋅WKvi=xi⋅WVαi,j=softmax(d
qi⋅kjT)oi=j∑αi,j⋅vj
在绝对位置编码下,上面的
x
x
x如果是在Transformer的第一层,则需要首先做绝对位置嵌入
x
i
=
x
i
′
+
p
i
x_i=x'_i + p_i
xi=xi′+pi.
而对于相对位置编码,无需做这种嵌入,而是在Attention score上增加惩罚,如下:
α
i
,
j
=
s
o
f
t
m
a
x
(
q
i
⋅
(
k
i
T
+
R
i
,
j
K
)
d
)
o
i
=
∑
j
α
i
,
j
⋅
(
v
j
+
R
i
,
j
V
)
\alpha_{i, j} = softmax(\frac {q_i·(k_i^T + R_{i,j}^K)}{\sqrt d}) \\ o_i = \sum_j \alpha_{i,j}· (v_j + R_{i,j}^V)
αi,j=softmax(d
qi⋅(kiT+Ri,jK))oi=j∑αi,j⋅(vj+Ri,jV)
其中
R
i
,
j
R_{i,j}
Ri,j便是相对位置信息,其大小只与(i-j)的取值有关,而与i、j分别取值多少无关。计算如下:
R
i
,
j
=
p
[
c
l
i
p
(
i
−
j
,
M
I
N
,
M
A
X
)
]
R_{i,j} = p[clip(i-j, MIN, MAX)]
Ri,j=p[clip(i−j,MIN,MAX)]
p是位置编码映射矩阵,clip是截断函数,确保任意输入都限制在MIN和MAX之间。这样一来,x的向量表示便和它所在的具体位置解耦,仅在Attention互动时考虑k、v的相对位置,更符合文本理解的习惯。
方案二
2019年,XLNET作为一种自回归编码器引起人们关注,在20+任务上超越BERT而给人留下深刻印象。XLNET的新颖之处不仅在于魔改BERT的结构为AR式,采用了PLM、双流注意力等全新的思路,还沿用了Transformer-XL的相对位置编码方法。这种方法将相对位置计算分解为四个部分,为便于理解和对比,首先我们给出带绝对位置编码的Attention计算展开式:
q
i
⋅
k
i
T
=
x
i
W
Q
W
K
T
x
j
T
+
x
i
W
Q
W
K
T
p
j
T
+
p
i
W
Q
W
K
T
x
j
T
+
p
i
W
Q
W
K
T
p
j
T
q_i·k_i^T = x_i W_QW_K^Tx_j^T + x_i W_QW_K^Tp_j^T + p_i W_QW_K^Tx_j^T +p_i W_QW_K^Tp_j^T
qi⋅kiT=xiWQWKTxjT+xiWQWKTpjT+piWQWKTxjT+piWQWKTpjT
而Transformer-XL则改动如下:
q
i
⋅
k
i
T
=
x
i
W
Q
W
K
T
x
j
+
x
i
W
Q
W
K
T
R
i
−
j
T
+
u
W
Q
W
K
T
x
j
T
+
v
W
Q
W
K
T
R
i
−
j
T
q_i·k_i^T = x_i W_QW_K^Tx_j + x_i W_QW_K^TR_{i-j}^T + u W_QW_K^Tx_j^T +v W_QW_K^TR_{i-j}^T
qi⋅kiT=xiWQWKTxj+xiWQWKTRi−jT+uWQWKTxjT+vWQWKTRi−jT
其中R_{i-j}是相对位置向量,不能训练,论文中强调是采用Transformer一样的Sinusoidal生成方法;u、v是可训练的缺省向量。上述展开式分别做如下说明:
- Part 1: 基于内容的“寻址”,即没有添加原始位置编码的原始分数;
- Part 2: 基于内容的位置偏置,即相对于当前内容的位置偏差;
- Part 3: 全局的内容偏置,用于衡量key的重要性。文中认为对一个token的Attention计算时,q一样时会影响对k的评价,因此单独使用一项k编码以解耦q的影响;
- Part 4: 全局的位置偏置,作用与3类似。
还有一点值得注意的是,Transformer-XL的编码并未作用在v上,这点和方案一也不同,计算时直接使用了v的特征。
RoPE原理及实现
理论部分
假设两个词嵌入向量
x
q
x_q
xq、
x
k
x_k
xk,分别存在于位置m、n,则它们的位置编码向量如下:
q
m
=
f
q
(
x
q
,
m
)
k
n
=
f
k
(
x
k
,
n
)
q_m=f_q(x_q, m) \\ k_n=f_k(x_k, n)
qm=fq(xq,m)kn=fk(xk,n)
由于Attention计算的内积形式
q
m
T
k
n
q_m^Tk_n
qmTkn,因此首先假设内积运算下的恒等关系如下:
q
m
T
k
n
=
<
f
q
(
x
q
,
m
)
,
f
k
(
x
k
,
n
)
>
=
g
(
x
q
,
x
k
,
n
−
m
)
q_m^Tk_n=<f_q(x_q, m), f_k(x_k, n)>=g(x_q, x_k, n-m)
qmTkn=<fq(xq,m),fk(xk,n)>=g(xq,xk,n−m)
由于
x
q
,
x
k
x_q, x_k
xq,xk都是不依赖位置的纯Embedding表示,上述恒等式代表
q
m
T
k
n
q_m^Tk_n
qmTkn只与(n-m)有关,即(n-m)恒定时保持一致结果;
其次需要保证token在位置0时,不存在任何位置信息,即满足如下公式:
q
=
f
q
(
x
q
,
0
)
k
=
f
k
(
x
k
,
0
)
q=f_q(x_q, 0) \\ k=f_k(x_k, 0)
q=fq(xq,0)k=fk(xk,0)
因此现在需要寻找一种编码方案
f
q
,
f
k
f_q, f_k
fq,fk. 首先假设向量维度大小为2,利用向量在2D空间中的几何意义及其在复数下的表示,分解上述公式为复数的指数形式,如下:

其中R和
θ
\theta
θ分别表示复数的实部和虚部,代入得到:

同时由于位置0的约束条件,又有:

接下来令m=n的情况,有:
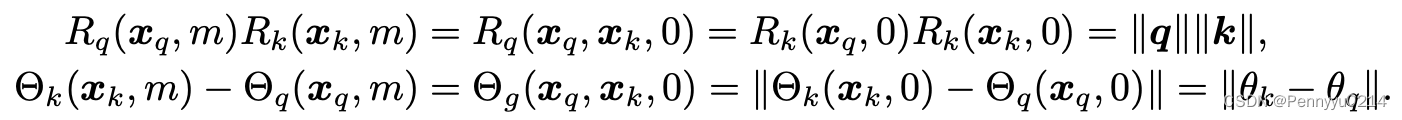
上述公式的意义为,如果两个token处于一个位置,那么应有距离为0的相对位置表示,同时也应与两个token在位置0时的表示一致。上式进一步推导如下:
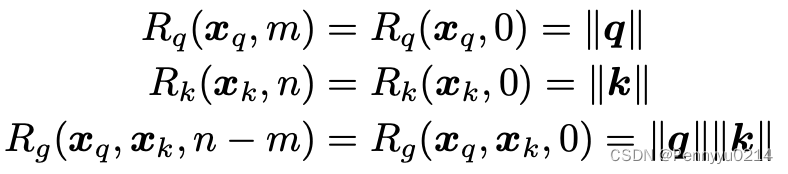
可以解释为R是和位置信息无关的,而
θ
\theta
θ和Q、K也无关,因此给出下式:
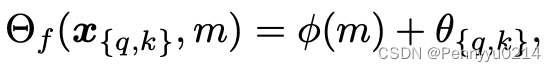
其中
ϕ
\phi
ϕ是word embedding,将
Θ
f
(
x
{
q
,
k
}
,
m
)
−
θ
{
q
,
k
}
\Theta_f(x_{\{q, k\}},m)-\theta_{\{q,k\}}
Θf(x{q,k},m)−θ{q,k}表示为一种位置m的函数。进一步地,令n=m+1,上式变为:
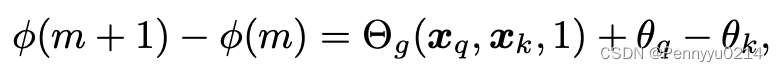
由于RHS是一个与m无关的常数,连续整数输入的φ(m)产生一个算术级数:

总结上述推导形式如下:
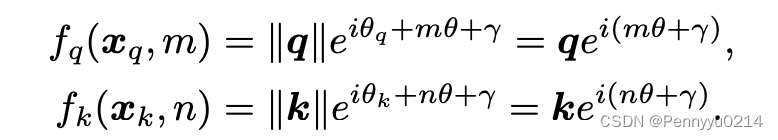
为了满足位置0的情况,定义:
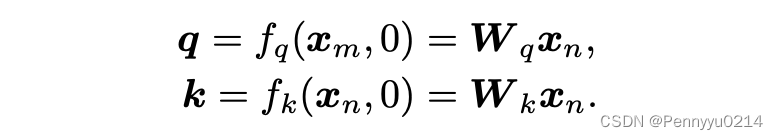
设
γ
=
0
\gamma=0
γ=0,得到最终表示形式:
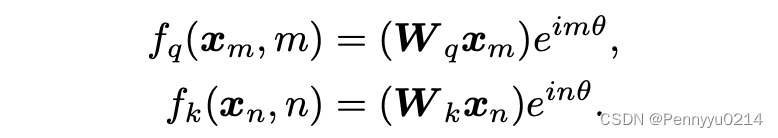
到此,RoPE的理论推导部分结束了。
高效实现
本节我们从RoPE最终实现的角度讨论它的原理和意义,首先给出论文3.4.2的旋转矩阵乘积实现,如下所示:
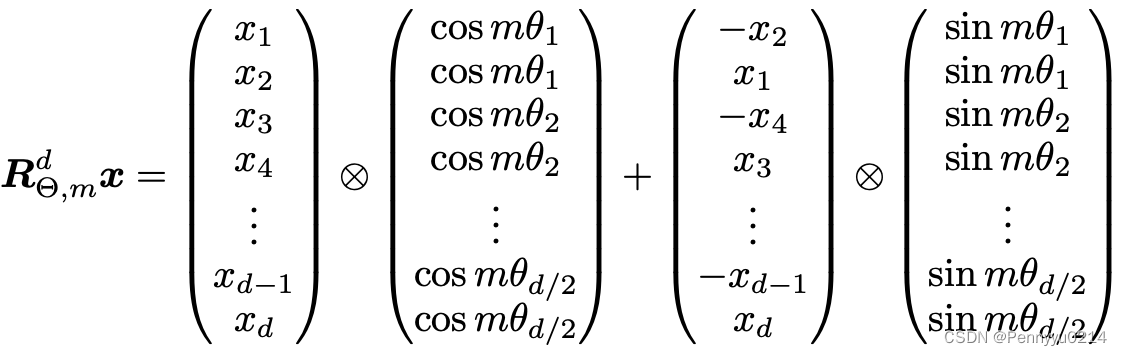
对于
m
θ
i
m\theta_i
mθi,有
m
θ
i
=
m
1000
0
2
i
/
d
m\theta_i = \frac {m}{10000^{2i/d}}
mθi=100002i/dm
我们从中也能看出,其实最终实现时就做了两步:1、最后一维重组(两两结合);2、三角函数乘积(第一项乘cos,第二项乘sin)。至于复数在这里面起什么作用呢?实际做上述计算时利用了复数乘积(特征虚数 * 三角函数虚数)以达到高效的目的,这点在下文探讨RoPE代码实现时会进一步说明。
几何意义
讲到这里,我们基本掌握了旋转位置编码的实现过程了。但这背后的原理还是不太清楚,旋转位置编码是怎么通过融入绝对位置信息实现相对位置表示的呢?旋转的思想体现在哪里?本节我们从平面坐标旋转的角度剖析RoPE,感受它的绝妙之处。
首先,我们假设向量隐层维度为2,即前文实现可以简化为:
R
Θ
,
m
d
x
=
(
x
1
x
2
)
⊗
(
c
o
s
m
θ
1
c
o
s
m
θ
1
)
+
(
−
x
2
x
1
)
⊗
(
s
i
n
m
θ
1
s
i
n
m
θ
1
)
R_{\Theta, m}^d x=
上式进一步表示为:
R
Θ
,
m
d
x
=
(
x
1
⋅
c
o
s
m
θ
1
−
x
2
⋅
s
i
n
m
θ
1
x
1
⋅
s
i
n
m
θ
1
+
x
2
⋅
c
o
s
m
θ
1
)
=
(
c
o
s
m
θ
1
,
−
s
i
n
m
θ
1
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
(
x
1
x
2
)
R_{\Theta, m}^d x=
不知读者看出来了吗,上式第二行的改写形式体现了向量旋转的思想,回顾下高中的平面坐标向量旋转公式:在平面直角坐标系中,对于向量(x, y),将其沿逆时针方向旋转角度
α
\alpha
α之后得到的
(
x
′
,
y
′
)
(x', y')
(x′,y′)可以计算为:
x
′
=
x
⋅
c
o
s
α
−
y
⋅
s
i
n
α
y
′
=
x
⋅
s
i
n
α
+
y
⋅
c
o
s
α
x' = x \sdot cos \ \alpha - y \sdot sin \ \alpha \\ y' = x \sdot sin \ \alpha + y \sdot cos \ \alpha
x′=x⋅cos α−y⋅sin αy′=x⋅sin α+y⋅cos α
如果是顺时针旋转,则计算变为:
x
′
=
x
⋅
c
o
s
α
+
y
⋅
s
i
n
α
y
′
=
−
x
⋅
s
i
n
α
+
y
⋅
c
o
s
α
x' = x \sdot cos \ \alpha +y \sdot sin \ \alpha \\ y' = -x \sdot sin \ \alpha + y \sdot cos \ \alpha
x′=x⋅cos α+y⋅sin αy′=−x⋅sin α+y⋅cos α
上述公式转写为矩阵乘法分别为:
(
x
′
y
′
)
=
(
c
o
s
α
,
−
s
i
n
α
s
i
n
α
,
c
o
s
α
1
)
(
x
y
)
可以看出,上式1和RoPE的计算一致,因此RoPE可以理解为将特征向量逆时针旋转
m
θ
1
m\theta_1
mθ1的角度。我们再来分析
q
T
k
q^Tk
qTk的情况,当q、k都获得RoPE编码后,计算如下:
q
=
R
m
q
′
k
=
R
n
k
′
q
T
k
=
(
R
m
q
′
)
T
R
n
k
′
=
q
′
T
R
m
T
R
n
k
′
=
q
′
T
(
R
m
T
R
n
)
k
′
=
q
′
T
(
c
o
s
m
θ
1
,
−
s
i
n
m
θ
1
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
T
(
c
o
s
n
θ
1
,
−
s
i
n
n
θ
1
s
i
n
n
θ
1
,
c
o
s
n
θ
1
)
k
′
q = R_mq' \\ k = R_nk' \\ q^Tk = (R_mq')^TR_nk' = q'^TR_m^TR_nk' = q'^T(R_m^TR_n)k' = \\q'^T
相信读者看出来了,左边的
(
c
o
s
m
θ
1
,
−
s
i
n
m
θ
1
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
T
q
m
T
k
n
=
<
f
q
(
x
q
,
m
)
,
f
k
(
x
k
,
n
)
>
=
g
(
x
q
,
x
k
,
n
−
m
)
q_m^Tk_n=<f_q(x_q, m), f_k(x_k, n)>=g(x_q, x_k, n-m)
qmTkn=<fq(xq,m),fk(xk,n)>=g(xq,xk,n−m)
我们再来看pos等于0的情况,即token处于位置开头时,能不能满足假设。设m=0,则
(
c
o
s
m
θ
1
,
−
s
i
n
m
θ
1
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
=
(
c
o
s
0
,
−
s
i
n
0
s
i
n
0
,
c
o
s
0
)
=
(
1
,
0
0
,
1
)
看出来矩阵变成了单位矩阵,则乘以特征向量后不会有任何变化,满足了假设:
q
=
f
q
(
x
q
,
0
)
k
=
f
k
(
x
k
,
0
)
q=f_q(x_q, 0) \\ k=f_k(x_k, 0)
q=fq(xq,0)k=fk(xk,0)
再来看m=n的情况,同样是代入公式,有:
q
T
k
=
q
′
T
(
c
o
s
m
θ
1
,
−
s
i
n
m
θ
1
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
T
(
c
o
s
n
θ
1
,
−
s
i
n
n
θ
1
s
i
n
n
θ
1
,
c
o
s
n
θ
1
)
k
′
=
q
′
T
(
c
o
s
m
θ
1
,
−
s
i
n
m
θ
1
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
T
(
c
o
s
m
θ
1
,
−
s
i
n
m
θ
1
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
k
′
q^Tk = \\q'^T
我们发现:
q
′
T
(
c
o
s
m
θ
1
,
−
s
i
n
m
θ
1
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
T
(
c
o
s
m
θ
1
,
−
s
i
n
m
θ
1
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
k
′
=
q
′
T
(
c
o
s
m
θ
1
,
s
i
n
m
θ
1
−
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
(
c
o
s
m
θ
1
,
−
s
i
n
m
θ
1
s
i
n
m
θ
1
,
c
o
s
m
θ
1
)
k
′
=
q
′
T
(
c
o
s
2
m
θ
1
+
s
i
n
2
m
θ
1
,
−
c
o
s
m
θ
1
⋅
s
i
n
m
θ
1
+
s
i
n
m
θ
1
⋅
c
o
s
m
θ
1
−
s
i
n
m
θ
1
⋅
c
o
s
m
θ
1
+
c
o
s
m
θ
1
⋅
s
i
n
m
θ
1
,
(
−
s
i
n
m
θ
1
)
2
+
c
o
s
2
m
θ
1
)
k
′
=
q
′
T
(
1
,
0
0
,
1
)
k
′
=
q
′
T
k
q'^T
同样满足假设:
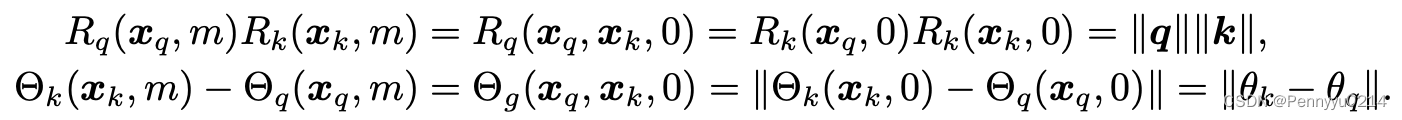
至此RoPE的原理剖析结束,旋转位置编码的“旋转”思想也展现得充分而深刻。以上推论既能反映RoPE的核心理念,也能解释为什么它具有强外推性(扩展或插值)的原因。
代码实现
LLaMA
本节通过分析RoPE的Pytorch代码来加深理解,将分别介绍RoPE在LLaMA和PaLM上的具体实现过程。首先给出LLaMA上的RoPE嵌入代码:
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
t = torch.arange(end, device=freqs.device) # type: ignore
freqs = torch.outer(t, freqs).float() # type: ignore
freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64
return freqs_cis
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
ndim = x.ndim
assert 0 <= 1 < ndim
assert freqs_cis.shape == (x.shape[1], x.shape[-1])
shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
return freqs_cis.view(*shape)
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
return xq_out.type_as(xq), xk_out.type_as(xk)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
能够看出总共由3个方法构成,分别是precompute_freqs_cis()、apply_rotary_emb()和reshape_for_broadcast()。首先分析precompute_freqs_cis(),一共五行代码,做了如下操作:首先初始化步长为2、长度为dim//2的基数向量,再同长度为L的位置索引向量做笛卡尔积(outer()方法),为后面的三角函数位置编码构建了目标值;polar用于创建极坐标对应的笛卡尔系坐标,代码中以1为绝对值,以freqs为角度,计算过程如下:
p
o
l
a
r
(
x
,
y
)
=
x
⋅
c
o
s
(
y
)
+
x
⋅
s
i
n
(
y
)
⋅
j
polar(x, y) = x\sdot cos(y) + x\sdot sin(y) \sdot j
polar(x,y)=x⋅cos(y)+x⋅sin(y)⋅j
最终freqs_cis大概如下:
(
c
o
s
0
1000
0
0
/
d
+
s
i
n
0
1000
0
0
/
d
⋅
j
,
c
o
s
0
1000
0
2
/
d
+
s
i
n
0
1000
0
2
/
d
⋅
j
,
.
.
.
c
o
s
1
1000
0
0
/
d
+
s
i
n
1
1000
0
0
/
d
⋅
j
,
c
o
s
1
1000
0
2
/
d
+
s
i
n
1
1000
0
2
/
d
⋅
j
,
.
.
.
.
.
.
,
.
.
.
,
.
.
.
)
再来看apply_rotary_emb(),其实里面分别对q、k执行了相同操作,这里单以q来分析。首先对q做维度变换,将原来dim的维度变换为[dim//2, 2],相当于对dim中的每一个偶数位置p的值,将其与p+1位置的相邻值结合。view_as_complex()方法将结合的二元组转换为复数,如下:
v
i
e
w
_
a
s
_
c
o
m
p
l
e
x
(
x
p
,
x
p
+
1
)
=
x
p
+
x
p
+
1
⋅
j
view\_as\_complex(x_p, x_{p+1}) = x_p + x_{p+1} \sdot j
view_as_complex(xp,xp+1)=xp+xp+1⋅j
reshape_for_broadcast()用于根据xq_变换维度,由于xq_是[B, L, H, dim//2, 1]维,freqs_cis是[L, dim//2]维,因此将freqs_cis扩充为[1, L, 1, dim//2, 1];紧接着xq_ * freqs_cis执行position-wise复数乘积运算,我们考虑[0, m, 0, i, 0]位置两个张量的乘积,首先xq_中对应位置的内容为
[
x
1
+
x
2
⋅
j
]
[x_1 + x_2 \sdot j]
[x1+x2⋅j],freqs_cis为
[
c
o
s
m
1000
0
2
i
/
d
+
s
i
n
m
1000
0
2
i
/
d
⋅
j
]
[cos \frac {m}{10000^{2i/d}} + sin \frac {m}{10000^{2i/d}} \sdot j]
[cos100002i/dm+sin100002i/dm⋅j],二者执行乘积运算结果如下:
[
x
1
+
x
2
⋅
j
]
∗
[
c
o
s
m
1000
0
2
i
/
d
+
s
i
n
m
1000
0
2
i
/
d
⋅
j
]
=
x
1
⋅
c
o
s
m
1000
0
2
i
/
d
+
x
1
⋅
s
i
n
m
1000
0
2
i
/
d
⋅
j
+
x
2
⋅
c
o
s
m
1000
0
2
i
/
d
⋅
j
−
x
2
⋅
s
i
n
m
1000
0
2
i
/
d
=
x
1
⋅
c
o
s
m
1000
0
2
i
/
d
−
x
2
⋅
s
i
n
m
1000
0
2
i
/
d
+
(
x
1
⋅
s
i
n
m
1000
0
2
i
/
d
+
x
2
⋅
c
o
s
m
1000
0
2
i
/
d
)
⋅
j
[x_1 + x_2 \sdot j]*[cos \frac {m}{10000^{2i/d}} + sin \frac {m}{10000^{2i/d}} \sdot j]=x_1\sdot cos \frac {m}{10000^{2i/d}} + x_1\sdot sin \frac {m}{10000^{2i/d}} \sdot j + x_2 \sdot cos \frac {m}{10000^{2i/d}} \sdot j - x_2 \sdot sin \frac {m}{10000^{2i/d}}\\=x_1\sdot cos \frac {m}{10000^{2i/d}} - x_2 \sdot sin \frac {m}{10000^{2i/d}} + (x_1\sdot sin \frac {m}{10000^{2i/d}} + x_2 \sdot cos \frac {m}{10000^{2i/d}}) \sdot j
[x1+x2⋅j]∗[cos100002i/dm+sin100002i/dm⋅j]=x1⋅cos100002i/dm+x1⋅sin100002i/dm⋅j+x2⋅cos100002i/dm⋅j−x2⋅sin100002i/dm=x1⋅cos100002i/dm−x2⋅sin100002i/dm+(x1⋅sin100002i/dm+x2⋅cos100002i/dm)⋅j
将
m
1000
0
2
i
/
d
\frac {m}{10000^{2i/d}}
100002i/dm表示成
m
θ
i
m\theta_i
mθi,上式转写成:
原式
=
x
1
⋅
c
o
s
m
θ
i
−
x
2
⋅
s
i
n
m
θ
i
+
(
x
1
⋅
s
i
n
m
θ
i
+
x
2
⋅
c
o
s
m
θ
i
)
⋅
j
原式=x_1\sdot cos\;m\theta_i - x_2 \sdot sin\; m\theta_i + (x_1\sdot sin \; m\theta_i + x_2 \sdot cos\; m\theta_i) \sdot j
原式=x1⋅cosmθi−x2⋅sinmθi+(x1⋅sinmθi+x2⋅cosmθi)⋅j
相信读者看出来了,上式结果的实部是2i处的旋转位置编码,虚部是2i+1处的旋转位置编码,与前文高效实现的过程一致。最终使用view_as_real()按实部、虚部切分成两个维度,再使用flatten()变形到dim维,就能够与q向量一致了。到此LLaMA的代码讲解结束了,应该说LLaMA的RoPE实现是很符合原始论文思想的,巧妙利用了虚数乘积进行奇数/偶数维编码计算。
PaLM
我们再来分析下PaLM中的代码实现,如下:
import torch
from einops import rearrange
from torch import einsum, nn
...
class RotaryEmbedding(nn.Module):
def __init__(self, dim):
super().__init__()
inv_freq = 1.0 / (10000 ** (torch.arange(0, dim, 2).float() / dim))
self.register_buffer("inv_freq", inv_freq)
def forward(self, max_seq_len, *, device):
seq = torch.arange(max_seq_len, device=device, dtype=self.inv_freq.dtype)
freqs = einsum("i, j->i j", seq, self.inv_freq)
return torch.cat((freqs, freqs), dim=-1)
def rotate_half(x):
x = rearrange(x, "... (j d) -> ... j d", j=2)
x1, x2 = x.unbind(dim=-2)
return torch.cat((-x2, x1), dim=-1)
def apply_rotary_pos_emb(pos, t):
return (t * pos.cos()) + (rotate_half(t) * pos.sin())
class ParallelTransformerBlock(nn.Module):
def __init__(self, dim, dim_head=64, heads=8, ff_mult=4):
super().__init__()
...
self.rotary_emb = RotaryEmbedding(dim_head)
...
def get_rotary_embedding(self, n, device):
if self.pos_emb is not None and self.pos_emb.shape[-2] >= n:
return self.pos_emb[:n]
pos_emb = self.rotary_emb(n, device=device)
self.register_buffer("pos_emb", pos_emb, persistent=False)
return pos_emb
def forward(self, x):
...
positions = self.get_rotary_embedding(n, device)
q, k = map(lambda t: apply_rotary_pos_emb(positions, t), (q, k))
...
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
首先看RotaryEmbedding(),同样init()中的inv_freq是一个基值向量,forward()初始化长度L的索引向量,然后对二者做笛卡尔积运算,代码中使用torch.einsum()表达式方法,'i, j->i j’表示分别输入尺寸为[i]、[j]的向量,做笛卡尔运算得到尺寸为[i, j]的矩阵。最后在-1维做一次拷贝、拼接,这里就和LLaMA不同了,因为PaLM是前dim//2维分别和后dim//2维组合,而LLaMA是相邻的x之间组合。
然后是apply_rotary_pos_emb(),t * pos.cos()代表让q、k分别与cos运算的position做点乘;rotate_half()中,rearrange(x, “… (j d) -> … j d”, j=2)将q或k张量最后一维重排成(j, d)尺寸,且j强制为2,这个操作实质是将dim维度的前后半部分切分,使原来维度为(B, H, N, D)的q或k变为(B, H, N, 2,D//2);unbind()将变换后的张量按-2维度切分为两组(即两个(B, H, N, D//2)的张量x1、x2,分别容纳-2维的第一项、第二项),并将x2取负值后与x1拼接成(B, H, N, D)维度,拼接时-x2在x1前面; r o t a t e _ h a l f ( t ) ∗ p o s . s i n ( ) rotate\_half(t) * pos.sin() rotate_half(t)∗pos.sin()得到变换后特征张量与position的sin运算相乘的结果,与之前的t * pos.cos()相加便得到了最终的旋转位置编码。
为了便于理解,我们使用一组示意图来说明:
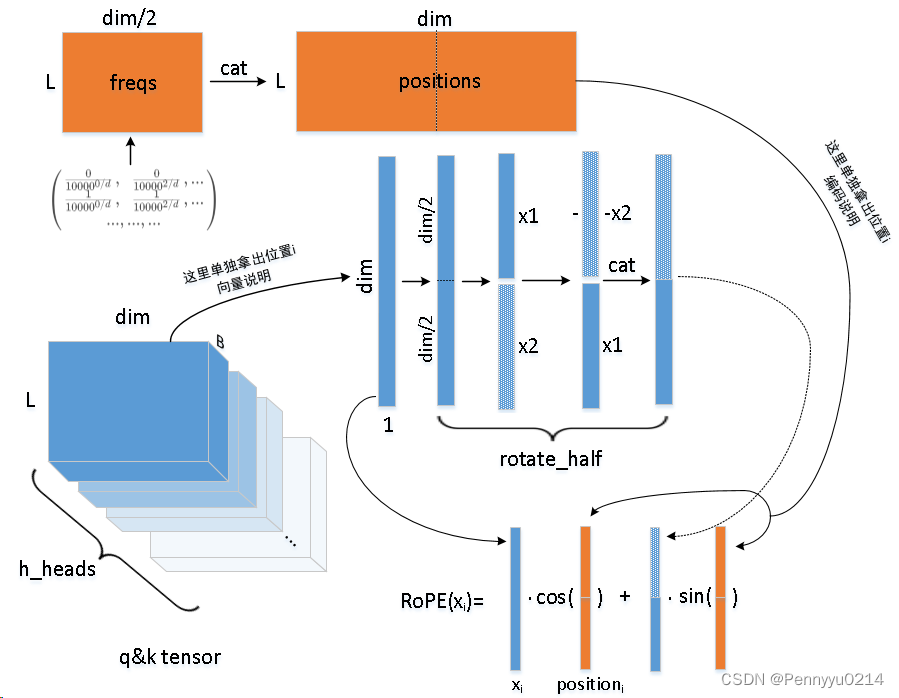
对于输入
x
i
x_i
xi中的某个分量
x
i
,
j
x_{i,j}
xi,j,上述RoPE实现的编码计算为:
R
o
P
E
(
x
i
,
j
)
=
x
i
,
j
⋅
c
o
s
0
1000
0
0
/
d
+
x
i
,
j
+
L
2
⋅
s
i
n
0
1000
0
0
/
d
RoPE(x_{i,j})=x_{i,j} \sdot cos\frac {0}{10000^{0/d}} + x_{i,j+\frac {L}{2}} \sdot sin\frac {0}{10000^{0/d}}
RoPE(xi,j)=xi,j⋅cos100000/d0+xi,j+2L⋅sin100000/d0
不同于LLaMA借助复数的思想,PaLM是直接通过张量变换实现了RoPE,里面涉及到了一些高级操作如rearrange()代替了reshape()变换,使用einsum()计算笛卡尔积等。虽方式不同但编码结果基本一致,唯一的区别就是二者的特征向量组合方法不同,LLaMA是偶数位与比它大一的奇数位,而PaLM则是隐层维度一分为二,每个分量一一对应。这两种实现从神经元的平坦角度讲几乎没有差别的,因为隐层范围内没有“位置编码”,神经元如何分布对模型不造成影响。
RoPE的优点
- RoPE是一种为Self-Attention量身打造的位置编码,针对Attention的点积查询设计了相对位置映射;
- 具有很好的可扩展性,包括采用外扩和内插等方法;
- RoPE编码能够随相对距离的增加而变得不明显(长期衰减性,Long-term decay),即目标token与当前token距离越远,则n-m的差异越大,所造成的旋转角度越大,进而向量的内积也越小。可以用cos和点积的关系理解,向量点积的计算方式如下:
q T k = ∣ ∣ q ∣ ∣ ⋅ ∣ ∣ k ∣ ∣ ⋅ c o s θ q^Tk = ||q||\sdot||k||\sdot cos\;\theta qTk=∣∣q∣∣⋅∣∣k∣∣⋅cosθ
其中为 θ \theta θ原始q、k的夹角。前文讲到距离在RoPE中通过旋转角度反映出来,则融入RoPE后q、k的点积计算为(假设旋转角度为p):
q T k = ∣ ∣ q ∣ ∣ ⋅ ∣ ∣ k ∣ ∣ ⋅ c o s ( θ + p ) q^Tk = ||q||\sdot||k||\sdot cos\;(\theta+p) qTk=∣∣q∣∣⋅∣∣k∣∣⋅cos(θ+p)
在 ∣ ∣ q ∣ ∣ ||q|| ∣∣q∣∣、 ∣ ∣ k ∣ ∣ ||k|| ∣∣k∣∣不变的情况下, q T k q^Tk qTk由 c o s ( θ + p ) cos\;(\theta+p) cos(θ+p)决定。由于相对距离越大则p越大,因此当p的绝对值足够大时会造成cos分布在较小的值,长度衰减性也体现出来了。
长度外推性
长度外推问题(Extrapolating )是验证长度大于训练最大长度的问题,传统的正余弦等绝对/相对位置编码的最大长度有限,超出长度时模型预测就会产生问题。具体地,如果训练时最大长度为512,则下式中i的范围为
i
∈
[
0
,
511
]
且
i
∈
N
+
i\in [0, 511]且i\in N^+
i∈[0,511]且i∈N+,如果预测时来了个长度600的输入,则模型无法编码位置大于512的部分,单靠将i的上界扩展至600也不行。这时一个有效方法是用一些长度在600以上的句子对模型微调,使用新模型在长样本上预测就可行了。但这种方法所带来的效果改善也是依位置编码不同而异,这就是长度外推性。
p
i
,
k
=
{
s
i
n
(
i
/
1000
0
2
t
/
d
)
k
=
2
t
c
o
s
(
i
/
1000
0
2
t
/
d
)
k
=
2
t
+
1
p_{i,k} =
不同的位置编码方案的长度外推性不同,近期的一些实验表明,像Sinusoidal等编码的外推性就不如RoPE,此外还有些工作如ALIBI是在注意力机制上下手,使用局部注意力机制以不受长度增长的影响,它们天然有着良好的外推性。
外推(Extrapolation)
我们针对RoPE的长度外推性展开探讨,目前主流的方案有两个:内插和外推。外推是指在现有位置范围的基础上沿最大位置向外扩展,如原来的i分布在 [ 0 , 511 ] [0, 511] [0,511]之间,如果要扩大一倍长度则在末尾增加 [ 512 , 1023 ] [512, 1023] [512,1023]即可,再用能匹配得上新位置的长句微调即可。但这样做一个问题是会导致Attention score的异常增加,影响到其性能。
内插(Interpolation)
内插就是在原来的离散位置之间插入新值,如原来的i取
[
0
,
511
]
[0, 511]
[0,511]之间的整数,内插方案就是在相邻整数之间插入新值,比如99,100之间插入99.5,这样整个原始长度范围内增加511个十分位为5的小数编码,与原来512的位置构成1023个位置容量,再用长句子微调即可。这篇工作《Extending Context Window of Large Language Models via Positional Interpolation》 正是采用这种位置插值(Position Interpolation, PI)将LLaMA扩展到32k长度,并且仅使用少量微调。


NTK
NTK(Neural Tangent Kernel)方案是最近有人提出的一种改进方法,主要解决内插法会造成位置i分布更加密集,模型难以区分先后顺序、位置大小等问题。具体做法是修改原来的线性插值为非线性,像之前的在0.5位置上插值属于线性插值,而非线性插值改变的不单是数量规模,而是分母上的“基数”,这个基数有可能会影响旋转编码的“转速”,大概的意思是线性插值会导致转速不均匀,而非线性则会带来向量空间的均匀位置变化,使模型更容易适应扩展位置。
对于这点,苏神引入了一个概念—位置
n
n
n的三角函数位置编码,本质上是数字
n
n
n的
β
β
β进制编码。要理解这句话,我们回顾一下对于一个数字n,如果取它的
β
\beta
β进制表示的右起第m位,如何计算呢?我们知道如果取的是右起第0位即最后一位,直接对
β
\beta
β取模即可;而m>0的情况,可以先右移m-1位,再对
β
\beta
β取模,另右移对应的是取整的除法计算,因此对
n
n
n取
β
\beta
β进制表示的右起第m位,有下列计算:
f
l
o
o
r
(
n
β
m
−
1
)
m
o
d
β
floor(\frac {n}{\beta^{m-1}})mod\;\beta
floor(βm−1n)modβ
其中floor代表向下取整,mod在式中代表对
β
\beta
β取余。
我们再来分析RoPE的计算公式,如下图所示。
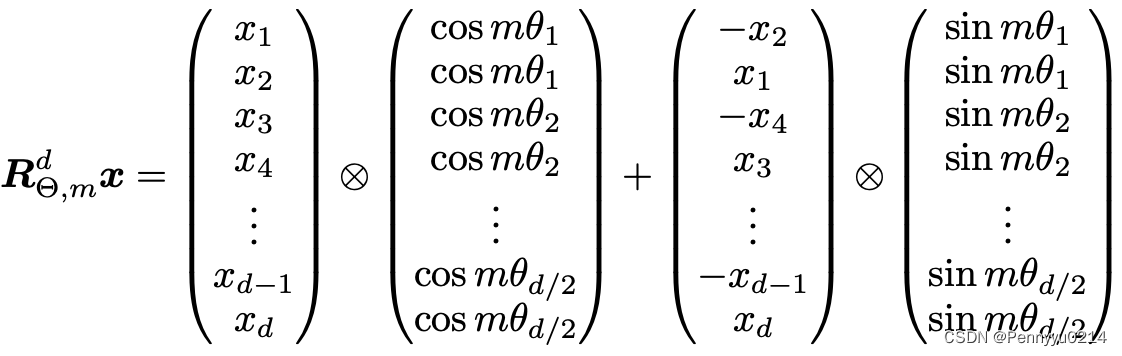
其中对于
m
θ
i
m\theta_i
mθi,有:
m
θ
i
=
m
1000
0
2
i
d
m\theta_i = \frac {m}{10000^{\frac {2i}{d}}}
mθi=10000d2im
其中i是以0开始的,我们记j=i+1,则公式变为:
m
θ
i
=
m
1000
0
2
(
j
−
1
)
d
m\theta_i = \frac {m}{10000^{\frac {2(j-1)}{d}}}
mθi=10000d2(j−1)m
再令
β
=
1000
0
2
d
\beta =10000^{\frac {2}{d}}
β=10000d2,上式变成:
m
θ
i
=
m
β
j
−
1
m\theta_i = \frac {m}{\beta^{j-1}}
mθi=βj−1m
对比前面的数位提取公式,我们看到上述形式与
f
l
o
o
r
(
)
floor()
floor()中完全一致了;对于floor取整,由于一个数取整与否与原来最多相差不超过1,因此一般情况下取整的影响可忽略不计;最后是取模运算,模运算和sin、cos三角函数一样具备周期性,但存在周期不同的情况,对于三角函数的周期是
2
π
2\pi
2π,而
β
=
1000
0
2
d
\beta=10000^{\frac {2}{d}}
β=10000d2,d代表向量维度,假设d取768,则
β
≈
1.02427522
\beta≈1.02427522
β≈1.02427522,意味着外层函数的周期需要与
β
\beta
β一致时才能体现出进制数位的特性,这里确实也令人困惑。
我们暂且忽略周期的影响,在一个理想情况下分析NTK方法的意义。首先设
β
=
4
\beta=4
β=4,这样
1000
0
2
d
=
4
10000^{\frac {2}{d}}=4
10000d2=4,得到
d
=
2
log
10000
4
d=\frac {2}{\log_{10000}^{4}}
d=log1000042(约等于13,相当于隐层维度)。据此分析位置编码与进制数位之间的关系,当
β
=
4
\beta=4
β=4时,
m
θ
i
m\theta_i
mθi计算如下:
m
θ
i
=
m
4
j
−
1
m\theta_i = \frac {m}{4^{j-1}}
mθi=4j−1m
不考虑取整的情况下,如果对
m
θ
i
m\theta_i
mθi取模
m
o
d
4
mod\;4
mod4,即含义是token所在位置m的四进制表示的右起第j位,而j-1又代表当前数值在向量维度中的索引,所以对于位置m的token,其Sinusoidal式的位置编码向量就可以理解为m的
β
\beta
β进制表示。我们用以下示意图来说明,对于
β
=
4
\beta=4
β=4的情况,不同位置(pos)的位置编码表示如下:
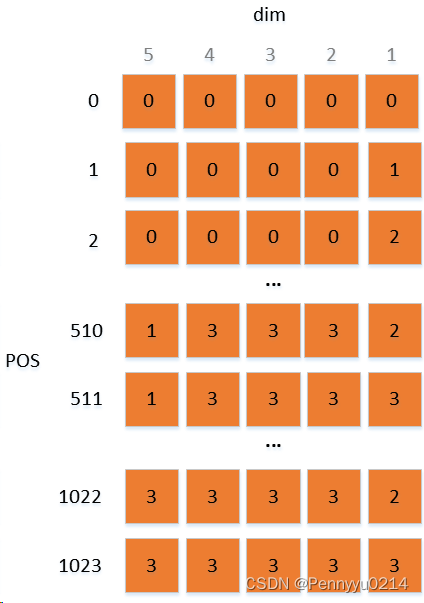
根据以上模型,我们重新考虑长度外推问题。首先是外推,对于原始模型1024的最大输入长度,如果外推到2048的推理长度,可以将m增加到2047并采取少量微调。当m增加后,从上述模型的视角看就是
β
\beta
β进制编码需要增加一位,因为原有的5位只能表示到1023. 这样看来,外推就成了在原有编码的基础上,高位增加一个新值,再进行一个1023长度的编码表示,有种内存的基址+变址寻址的感觉。而对于新的表示为1的基址,模型训练时没有获得相关特征,因此只能微调后使用。但由于基址后的偏移量与原始整体一致,都是1024位,因此也容易获得对齐的位置表征,外推性也得到确保。外推方法图说明如下:
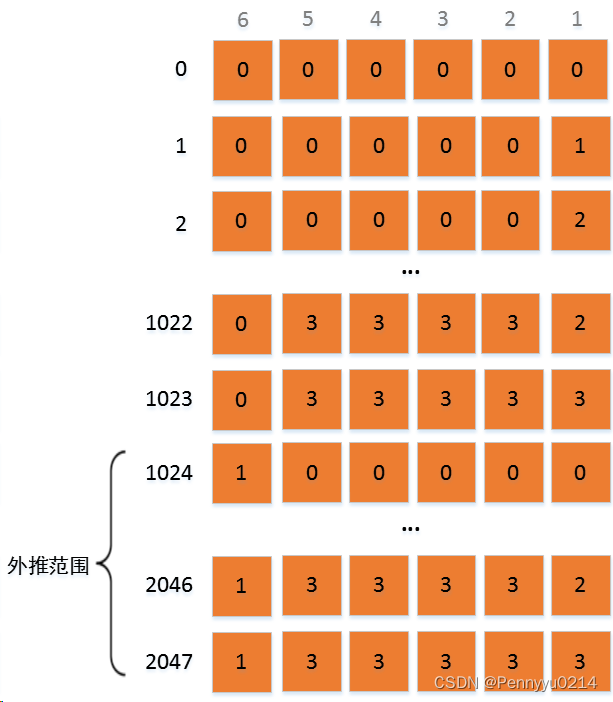
但由于外推将位置编码直接拉到一个模型从未见过的新范围,导致外推不是较好的方案。因此又出现了线性插值法,前文讲过线性插值是在相邻两个位置间的中点插入新位置,如100和101之间,插入100.5作为新位置。我们用上述的四进制表示模型来分析,当插入100.5时,其四进制表示为:
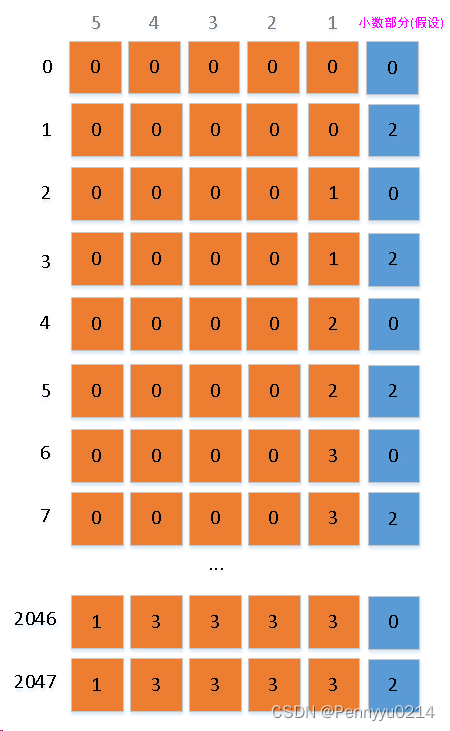
读者看出来了,与外推在高位增加数位的方式不同,内插在低位增加了数位,具体增加了四进制的-1次方指数位表示。这个表示在位置编码中是不直观存在的(因为向量的索引没有-1),上图为了思路清晰扩充了一排小数位,实际中小数位的量也会通过浮点计算反映出来。执行线性内插后原始为1的步长也变成了0.5,这样可以在不改变编码上界(1023)的情况下,通过稠密化表示获得2倍的位置编码。相比外推法,这样做模型会更好地编码长句,无需学习一个新的表示空间,仅从已学到的空间中进一步细化即可。
但是线性插值法依然存在问题,首先就是位置向量稠密化后,造成位置编码过于紧密,模型难以区分的情况,这种情况如果是低精度推理下,效果可能会变得更差;其次是由于Attention对近邻token的依赖性普遍较高,一旦内插导致近邻位置发生改变,对当前token的特征表示影响很大;再次就是转速不均匀,怎么理解转速不均匀呢?我们假设位置的进制表示是一列轮盘,每个轮盘的范围是0~3,轮盘转动一圈后自动复位,并带动下一个轮盘转动一步。首先看不加线性插值的编码进制表示,当位置均匀增加时,轮盘均匀转动,转到最大值时复位并带动下一个轮盘转动一步,以此类推,因此这种转动是匀速的;再看内插效果,同样位置均匀增加时,新增的小数位轮盘一次旋转两步,而转到最大值时,带动个位数的旋转却只有一步,因此不均匀就体现出来了。这种问题在模型训练时,会造成对新编码的适应效率低下问题,导致跳转较大的位置和较小的位置信息量不均衡。
总结起来,一个好的长度外推方案,至少应满足如下两个条件:
- 尽量不要在高位拓展数位,这样会将位置表示扩充到未训练的空间,影响模型效果;
- 外推后要确保位置均匀改变时,新编码的进制表示在各数位上依旧转速均匀,不能出现不同数位上转速失衡情况(后面的混合进制方案表明,由于不同位置编码的使用频率差异,这种转速也要依高、低位而均衡控制)。
或许此时读者应该想到了一个可行方案:既然进制表示的长度不能扩充,能不能扩充一下已有进制即base的范围?当
β
=
4
\beta=4
β=4时,长度5位的进制表示能支持的最大序列长度为1023,如果增加
β
\beta
β,比如扩充
β
\beta
β到6,即按六进制表示位置,则长度5的进制表示最大支持
6
5
=
7776
6^5=7776
65=7776,长度能够扩充到接近8k,同时还保证了上述两个条件:避免高位扩展和转速均匀。这就是NTK长度外推思想的一种直观化解释。以下是原理说明:
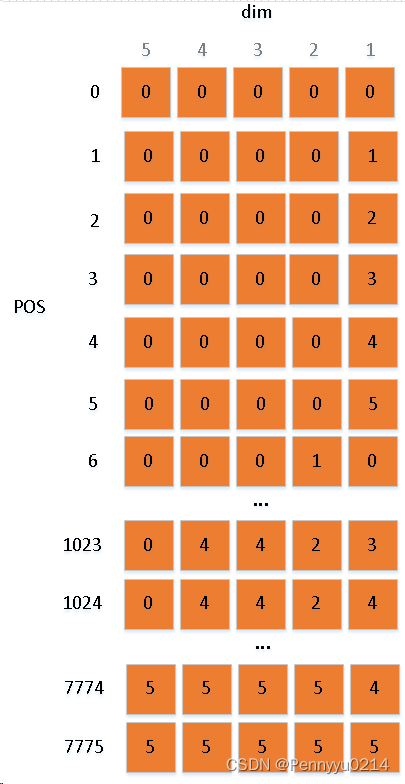
我们看出base扩充后,同样长度进制编码的表示容量提升了,同时进制的旋转步长也是均匀的1值。这种方案相比线性插值能够有效提升长度外推能力。因为在训练阶段,模型是按固定长度、固定转速学习位置编码的,外推时采用扩充base 的方式能够使模型适应同样长度和转速的新编码结构,效率提升同时效果也会更好。
而实际修改时将分母的
β
\beta
β乘上一个大于1的因子
λ
\lambda
λ,使最终外推到的n * k长度的编码等于原始位置n的编码,即可求出
λ
\lambda
λ的值,换句话讲,构建下列等式:
n
β
d
/
2
−
1
=
n
⋅
k
(
λ
⋅
β
)
d
/
2
−
1
\frac {n}{\beta^{d/2-1}}= \frac {n\sdot k}{(\lambda\sdot\beta)^{d/2-1}}
βd/2−1n=(λ⋅β)d/2−1n⋅k
解得
λ
=
k
2
d
−
2
\lambda=k^{\frac {2}{d-2}}
λ=kd−22
即得到在k倍外推下进制因子
λ
\lambda
λ的取值。后来又有了新方案,苏神认为不同相对位置的分布频率不同,存在低位多、高位少的情况,提出混合进制表示以均衡整体位置编码的训练。混合进制表示是指在不同数位上使用不同的base,例如进制序列[2,3,4,5]代表数位上的进制分布,如果整数
m
m
m的混合进制表示为abc,则
m
=
c
+
b
∗
5
+
a
∗
4
∗
5
m = c + b * 5 + a * 4 * 5
m=c+b∗5+a∗4∗5
此外每个数位上的大小应在对应的进制范围内,如c的范围是[0,4]且为整数,b的范围是[0,3]且为整数,a的范围是[0,2]且为整数。混合进制的特点如下:①不同数位的范围不同,如果当前数位+1,则整个数的增量等于后面(低位方向)所有数位的base之积;②存在上限,由于混合进制依赖具体的进制规范,因此能表示的最大数也是进制序列的积-1,即对于序列为[a,b,c,d]的混合进制,其表示的最大值m为:
m
=
∏
i
∈
[
a
,
b
,
c
,
d
]
i
m = \prod_{i\in[a,b,c,d]} i
m=i∈[a,b,c,d]∏i
混合进制的应用较少,比如“上一下四”珠算利用“二五混合进制”的思想,即以序列[2,5]表示一个十进制数,即N=5A+B. 数位提取方法也略有不同,对于
b
=
[
b
1
,
b
2
,
.
.
.
,
b
m
]
b=[b_1,b_2,...,b_m]
b=[b1,b2,...,bm]混合进制表示的数n(如果不超上限),其在第a位(
1
≤
a
≤
m
1≤a≤m
1≤a≤m)上的数位计算为:
f
l
o
o
r
(
n
∏
i
=
m
−
a
+
2
m
b
i
)
m
o
d
b
m
−
a
+
1
floor(\frac {n}{\prod_{i=m-a+2}^{m}b_i})mod\;b_{m-a+1}
floor(∏i=m−a+2mbin)modbm−a+1
在混合进制的位置编码思想中,计算变为:
m
θ
i
=
m
1000
0
2
i
d
⋅
(
λ
1
.
.
.
λ
m
)
m\theta_i=\frac {m}{10000^\frac {2i}{d}\sdot (\lambda_1...\lambda_m)}
mθi=10000d2i⋅(λ1...λm)m
按照外推的目标,分母需要增加到k倍以良好适配,则
λ
1
.
.
.
λ
m
=
k
\lambda_1...\lambda_m=k
λ1...λm=k;同时要均衡地训练每个位置,对此做如下约束:
λ
1
≥
λ
2
≥
λ
3
≥
.
.
.
≥
λ
d
2
≥
1
\lambda_1≥\lambda_2≥\lambda_3≥...≥\lambda_\frac {d}{2}≥1
λ1≥λ2≥λ3≥...≥λ2d≥1
我们分析下这样做的意义,由于位置编码的进制特性,只有较大的位置表示下高位才能得到训练,而较小的位置表示只能训练到低位。而位置的使用也存在频率差异,表现为较大位置使用较少、较小位置使用较多,因此实际训练时高位可能存在训练不充分情况。为了均衡这种差异,需要将高位的表示适当压缩,低位的表示适当扩充,于是就有了由低位到高位递减的混合进制表示方法。混合进制表示中,当位置均匀增加时,低位由于进制base较大而转速较慢,可表示数位较多,能够容纳更多特征,在高频的使用下也能充分学习;而高位由于base较小,可表示数位较少,适用于不常见的长距离表示,无需过多特征。由此实现了均摊思想。
根据上述推论,我们在分析下前文说的线性插值法,前面说过线性插值法在两个已有位置编码之间均匀插入新位置,由此进制表示的小数位扩充一位,但分析时认为小数位存在转速不均匀情况。而从混合位置编码角度看,插入的小数位更新频率最大,但小数位只有‘0,2’两种表示,相当于二进制,表示能力不足以适应极高的使用频率,因此线性插值法的性能提升也存在上限。
对于
λ
\lambda
λ的确定,使用了一个函数来表示:
λ
1
λ
2
.
.
.
λ
m
=
e
a
⋅
m
b
\lambda_1\lambda_2...\lambda_m=e^{a\sdot m^b}
λ1λ2...λm=ea⋅mb
又
λ
1
λ
2
.
.
.
λ
d
2
=
k
\lambda_1\lambda_2...\lambda_{\frac {d}{2}}=k
λ1λ2...λ2d=k,因此
a
(
2
d
)
b
=
l
o
g
k
a(\frac {2}{d})^b=logk
a(d2)b=logk,a和b产生对应关系,实际只需调一个参数,这里没有统一的标准。
实验也表明了上述方案的有效性,有兴趣的小伙伴可以浏览他的原文
[
7
]
^{[7]}
[7]。
后面还提出了很多进一步优化的方法,如基于窗口w的分块方案 [ 8 ] ^{[8]} [8],主要是保护近邻位置的原始编码,只将远距离的位置稠密化,防止Attention计算时近邻token的信息变化,造成解码时出现问题。该方案理论上实现了无线长度外推,有兴趣可以前往原文查看。
参考链接
- Su J , Lu Y , Pan S ,et al.RoFormer: Enhanced Transformer with Rotary Position Embedding[J]. 2021.DOI:10.48550/arXiv.2104.09864.
- 让研究人员绞尽脑汁的Transformer位置编码
- https://link.zhihu.com/?target=https%3A//github.com/lucidrains/PaLM-pytorch/blob/main/palm_pytorch/palm_pytorch.py (RoPE的LLaMA实现)
- https://link.zhihu.com/?target=https%3A//github.com/facebookresearch/llama/blob/main/llama/model.py (RoPE的PaLM实现)
- https://arxiv.org/pdf/2306.15595.pdf
- https://www.reddit.com/r/LocalLLaMA/comments/14lz7j5/ntkaware_scaled_rope_allows_llama_models_to_have/
- https://kexue.fm/archives/9706
- https://kexue.fm/archives/9708


