devbox
笔触狂放9
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

动态规划入门：斐波那契数列模型以及多状态（C++）_c用动态规划法求解斐波那契问题

作者：笔触狂放9 | 2024-04-23 15:20:59

赞

踩

c用动态规划法求解斐波那契问题

斐波那契数列模型以及多状态

动态规划简述

    动态规划(Dynamic programming，简称 DP)是一种解决多阶段决策问题的算法思想。它将问题分解为多个阶段，并通过保存中间结果来避免重复计算，从而提高效率。


动态规划的解题步骤一般分为以下几步：

  1. 思考状态表示，创建dp表(重点)
  2. 分析出状态转移方程(重点)
  3. 初始化
  4. 确定填表顺序
  5. 确定返回值

斐波那契数列模型

1.第 N 个泰波那契数（简单）

链接：第 N 个泰波那契数

  • 题目描述

在这里插入图片描述

  • 做题步骤
  1. 状态表示

面对动态规划问题，我们一般有两种状态表示：

  1. 以某一个位置为起点，……
  2. 以某一个位置为终点，……

我们一般优先考虑第1种表示，但如果第1种无法解决就考虑第2种。

在这里插入图片描述

  1. 状态转移方程
    这个题目直接告诉了我们状态转移方程：dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

  2. 初始化
    泰波那契数的第0、1、2个是特殊的，不满足状态转移方程，因此我们需要初始化这三个位置为0、1、1

  3. 填表顺序
    保证填当前状态时，所需状态已经计算过，填表顺序很明显是从左往右

  4. 返回值
    根据状态表示，假设要求的是第n个，返回的应该是dp[n]

  • 代码实现
class Solution {
public:
    int tribonacci(int n) 
    {
        //对于第0、1、2单独处理
        if(n == 0) 
            return 0;
        if(n == 1 || n == 2)
            return 1;
        //dp[i]：第i个泰波那契数
        vector<int> dp(n + 1);
        dp[0] = 0; dp[1] = 1; dp[2] = 1; 
           
        for(int i = 3; i < n + 1; i++)
        {
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
        }
        return dp[n];
        //空间复杂度：O(N)
        //时间复杂度：O(N)
    }
};

//不知道大家有没有发现向后填表的过程其实只需要前置的3个状态
//其余的状态都是多余的，我们可以用有限的变量来保存这些状态，这样就实现了空间优化
//这种优化方式被称为“滚动数组”
//经过优化原O(N)->O(1) O(N^2)->O(N)
//但这并不是动态规划讲解的要点，所以我只会把两种优化情况的代码给出

// class Solution {
// public:
//     int tribonacci(int n) 
//     {
//         if(n == 0) 
//             return 0;
//         if(n == 1 || n == 2)
//             return 1;

//         int t1 = 0;
//         int t2 = 1;
//         int t3 = 1;
//         int ret = 0;
           
//         for(int i = 3; i < n + 1; i++)
//         {
//             ret = t1 + t2 + t3;
//             t1 = t2;
//             t2 = t3;
//             t3 = ret;
//         }
//         return ret;
//     }
// };

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53

2.三步问题（简单）

链接：三步问题

  • 题目描述
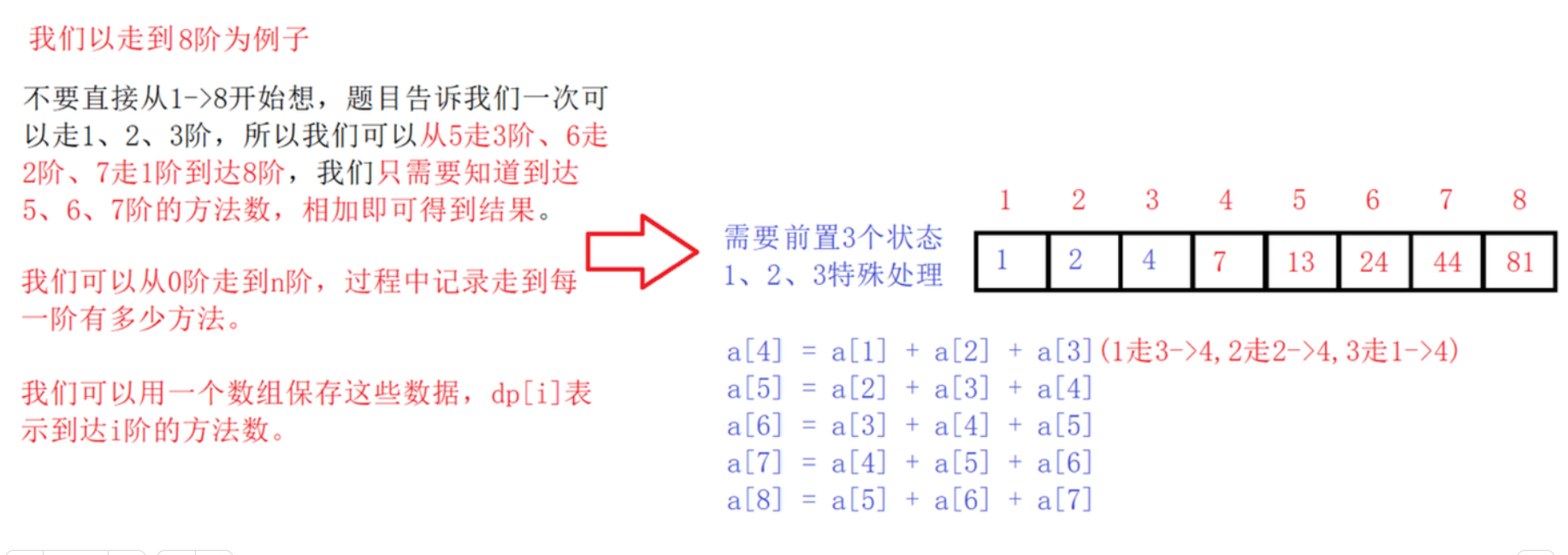
    在这里插入图片描述

  • 做题步骤

  1. 状态表示
    在这里插入图片描述

  2. 状态转移方程
    到达i阶可以转换成先到达i - 3、i - 2、i - 1阶，三者相加得到结果，所以状态转移方程为：dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]。

  3. 初始化
    为了保证填表不越界，我们把到达1、2、3阶的方法初始化。

  4. 填表顺序
    保证填当前状态时，所需状态已经计算过，填表顺序从左往右。

  5. 返回值
    根据状态表示，假设要求的是n阶，返回的应该是dp[n]

  • 代码实现
class Solution {
public:
    int waysToStep(int n) 
    {
        //1、2、3阶特殊处理
        if(n == 1) return 1;
        if(n == 2) return 2;
        if(n == 3) return 4;

        //dp[i]表示到达i阶的方法数
        vector<int> dp(n+1); //多开一个空间，可以让下标和层数对应
        dp[1] = 1; dp[2] = 2; dp[3] = 4;
        const int mod = 1e9 + 7;  //有可能超出，需要取模

        for(int i = 4; i < n + 1; i++)
        {
            dp[i] = ((dp[i-1] + dp[i-2]) % mod + dp[i-3]) % mod;
        }
        return dp[n];
        //时间复杂度：O(N)
        //空间复杂度：O(N)
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23

3.使⽤最⼩花费爬楼梯（简单）

链接：使⽤最⼩花费爬楼梯

  • 题目描述
    在这里插入图片描述

  • 做题步骤

  1. 状态表示
    这个题目的思路和第2题很相似，要到达终点n阶，我们可以从n - 1阶走一步、n - 2阶走两步到终点，从中选择费用最低的一方(从当前阶离开需要支付离开费用)；至于到达n - 1、n - 2阶的最低费用，我们可以以n - 1、n - 2层为终点进行分析，依此类推。到达终点的过程需要到达每一层的最低费用，我们可以用一个dp表存储，dp[i]表示到达下标i台阶所需要的最低费用。

  2. 状态转移方程
    到达i阶的最低花费可以转换为min(到达i - 1阶的最低花费 + 走出这一阶的花费， 到达i - 2阶的最低花费 + 走出这一阶的花费)，所以状态转移方程为：dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])。

  3. 初始化
    由转移方程可知更新某个状态需要前置的两个状态，为了确保填表时不越界，单独处理走到0、1阶的最低花费。

  4. 填表顺序
    保证填当前状态时，所需状态已经计算过，填表顺序从左往右。

  5. 返回值
    根据状态表示，假设数组有n个元素(终点是n阶)，返回的应该是dp[n]

  • 代码实现
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) 
    {      
        //dp[i] 表示到这一层的最小花费
        int n = cost.size();
        vector<int> dp(n + 1);
        //一开始就可以在0或1阶，花费为0，vector默认给0，不用处理

        for(int i = 2; i < n + 1; i++)
        {
            dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);
        }

        return dp[n];
        //空间复杂度：O(N)
        //时间复杂度：O(N)
    }
};

// //第二种写法：反着来，以某个位置为起点，……
// class Solution {
// public:
//     int minCostClimbingStairs(vector<int>& cost) 
//     {      
//         //dp[i]：这一层为起点，到终点的最低花费
//         int n = cost.size();
//         vector<int> dp(n + 1);
//         dp[n] = 0;
//         dp[n - 1] = cost[n - 1];
//         for(int i = n - 2; i >= 0; i--)
//         {            
//             dp[i] = min(dp[i + 1] + cost[i], dp[i + 2] + cost[i]);
//         }

//         return min(dp[0], dp[1]);
//     }
// };

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38

4.解码方法（中等）

链接：解码方法

  • 题目描述
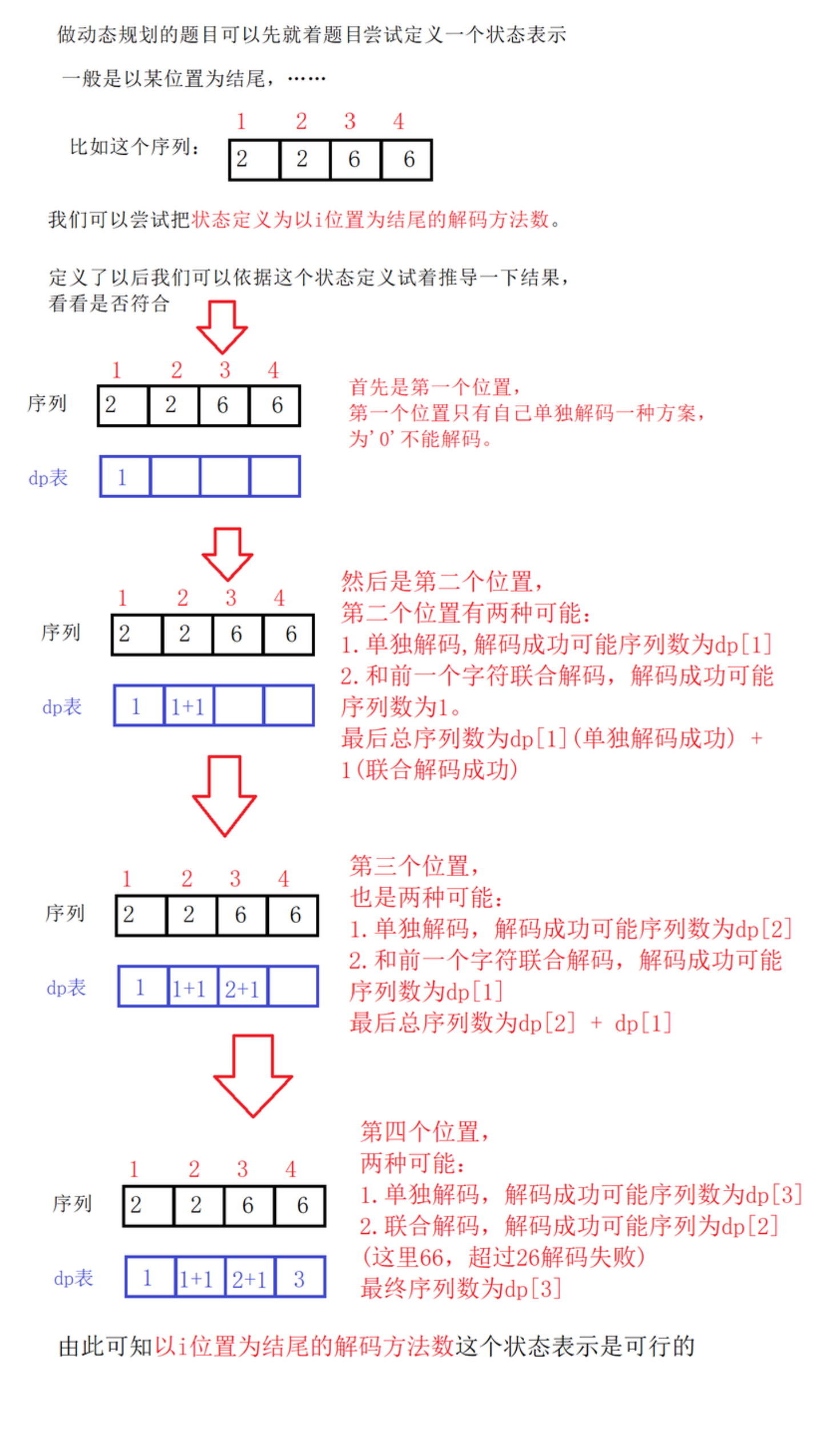
    在这里插入图片描述

  • 做题步骤

  1. 状态表示
    在这里插入图片描述

  2. 状态表示
    除去第一位，每个位置都有单独解码和联合解码两种方式，n位置的状态转移方程为：dp[n] = dp[n - 1]（单独解码成功）+ dp[n - 2]（联合解码成功）

  3. 初始化
    依据状态转移方程，某位置状态需要前置的两个状态，为了避免越界，我们需要单独处理第1、2个位置，但观察上面的分析过程，可以发现第2个位置和其它位置一样也有两种解码可能，我们可以在dp表前面多加个虚拟节点并初始为1，这样就只需要处理第1个位置了。（看图看图）

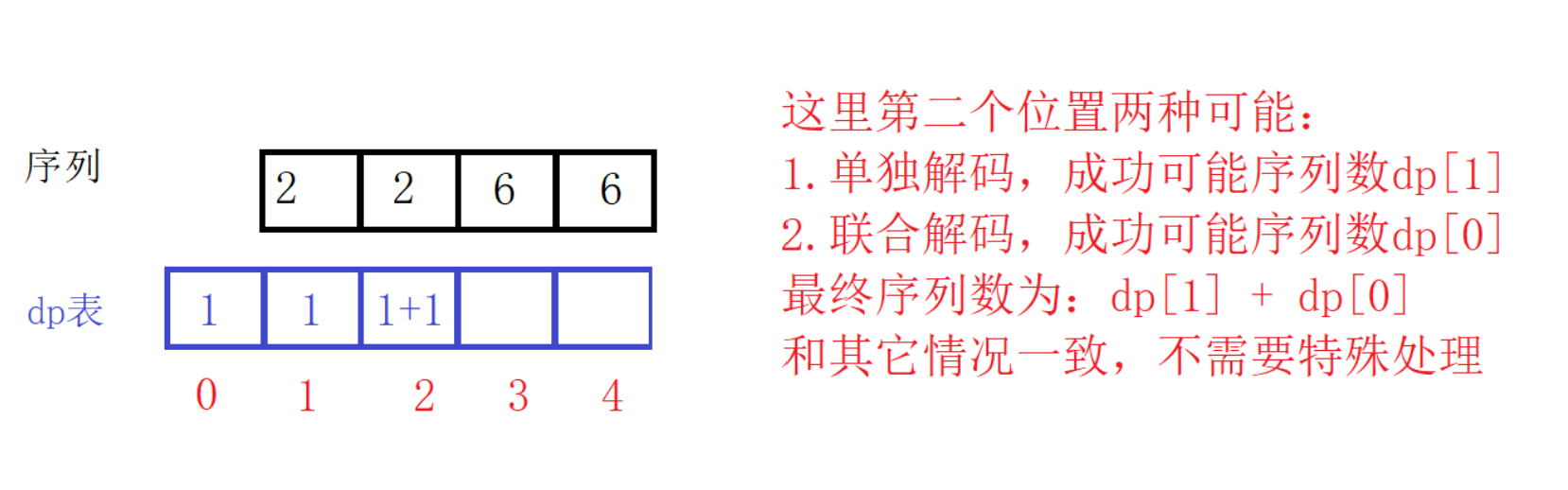
在这里插入图片描述

  1. 填表顺序
    保证填当前状态时，所需状态已经计算过，填表顺序从左往右。

  2. 返回值
    依据状态定义，假设序列长度为n，返回的应该是以n位置为结尾的解码可能数，即dp[n]。

  • 代码实现
class Solution {
public:
    int numDecodings(string s) 
    {
        int n = s.size();
        //dp[i]表示以i位置为结尾的解码可能数
        vector<int> dp(n + 1);
        //第一个位置就为0，最终结果已经是0
        if(s[0] == '0')
            return 0;
        //初始化虚拟节点和第1个位置
        dp[1] = dp[0] = 1;
        
        for(int i = 2; i < n + 1; i++)
        {
            //单独解码
            if(s[i - 1] != '0')                      
                dp[i] += dp[i-1];
            
            //联合解码（联合解码小于10说明存在前导0，无法联合解码）
            int com = (s[i - 2] - '0') * 10 + (s[i - 1] - '0');
            if(com >= 10 && com <= 26)                       
                dp[i] += dp[i-2];

            //都失败的情况是'00'，最终结果已经是0，这里可不加
            //两个连续的0，后面全都是0
            if(dp[i] == 0)
                return 0;        
        }

        return dp[n];
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33

简单多状态

1.打家劫舍（中等）

链接：打家劫舍

  • 题目描述
    在这里插入图片描述

  • 做题步骤

  1. 状态表示
    依据前面的做题经验，我们可以把状态表示为以i位置为结尾的最大偷窃金额，但每个位置有偷和不偷两种选择，所以可以把状态再进行细化：状态f表示以i位置为结尾并偷窃本位置的最大金额；状态g表示以i位置为结尾但不偷窃本位置的最大金额。

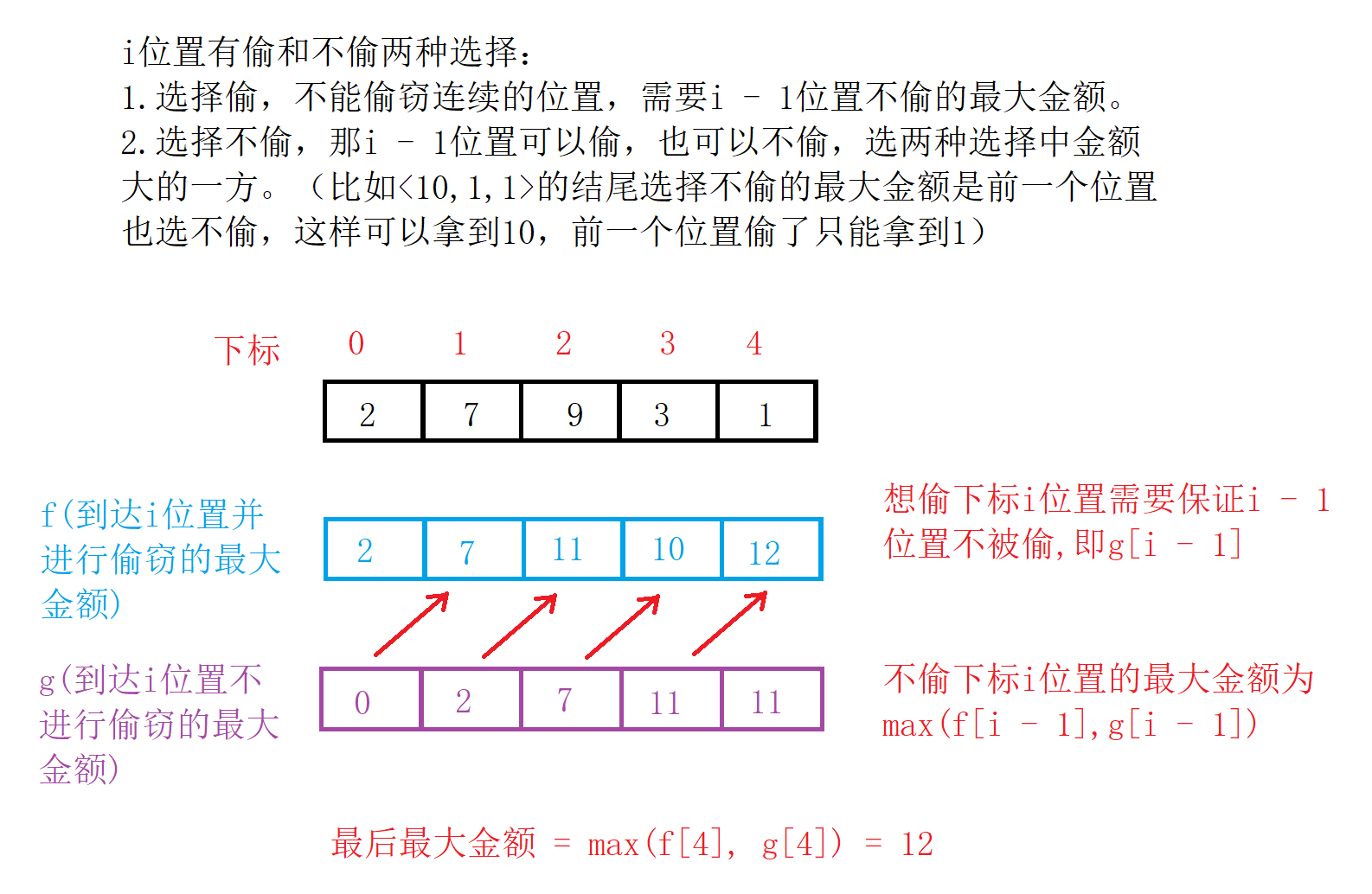
在这里插入图片描述

  1. 状态转移方程
    由前面的分析可知，要偷i位置(f)需要i - 1位置不偷(g)的最大金额，不偷i位置就选择i - 1位置偷和不偷两种选择中大的一方，所以状态转移方程为：
    (1) f[i] = g[i - 1] + nums[ i ] (本位置可偷金额)；
    (2) g[i] = max(g[i - 1], f[i - 1])

  2. 初始化
    由状态转移方程可知当今状态需要前一个状态，为保证填表时不越界，单独处理第一个位置：f[0] = nums[0]，g[0] = 0。

  3. 填表顺序
    保证填当前状态时，所需状态已经计算过，填表顺序从左往右。

  4. 返回值
    把自己代入成小偷，相邻位置不能同时偷的情况下是需要进行选择的，但偷的过程中不知道后面房子的价值，只能走一步看一步，保证每一步都是最好的，偷到最后一定是最优结果。假设数组有n个元素，返回值为max(f[n - 1], g[n - 1])。

  • 代码实现
class Solution {
public:
    int rob(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> f(n); //f[i]表示到底这个位置并偷窃的最大金额
        auto g = f;  //g[i]表示到达这个位置不偷窃的最大金额
        f[0] = nums[0]; //初始化f[0],g[0]默认0不用处理
        for(int i = 1; i < n; i++)
        {
            f[i] = g[i - 1] + nums[i];
            g[i] = max(g[i - 1], f[i - 1]);
        }
        return max(f[n - 1], g[n - 1]);
        //空间复杂度：O(N)
        //时间复杂度：O(N)
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18

2.打家劫舍II（中等）

链接：打家劫舍II

  • 题目描述
    在这里插入图片描述

  • 做题步骤

  1. 状态表示
    这个题和前一个题唯一的不同只有首尾成环这一个点，我们延用上个题目的状态表示：状态f表示以i位置为结尾并偷窃本位置的最大金额；状态g表示以i位置为结尾但不偷窃本位置的最大金额。
    处理成环问题，最直接的思路就是拆解。
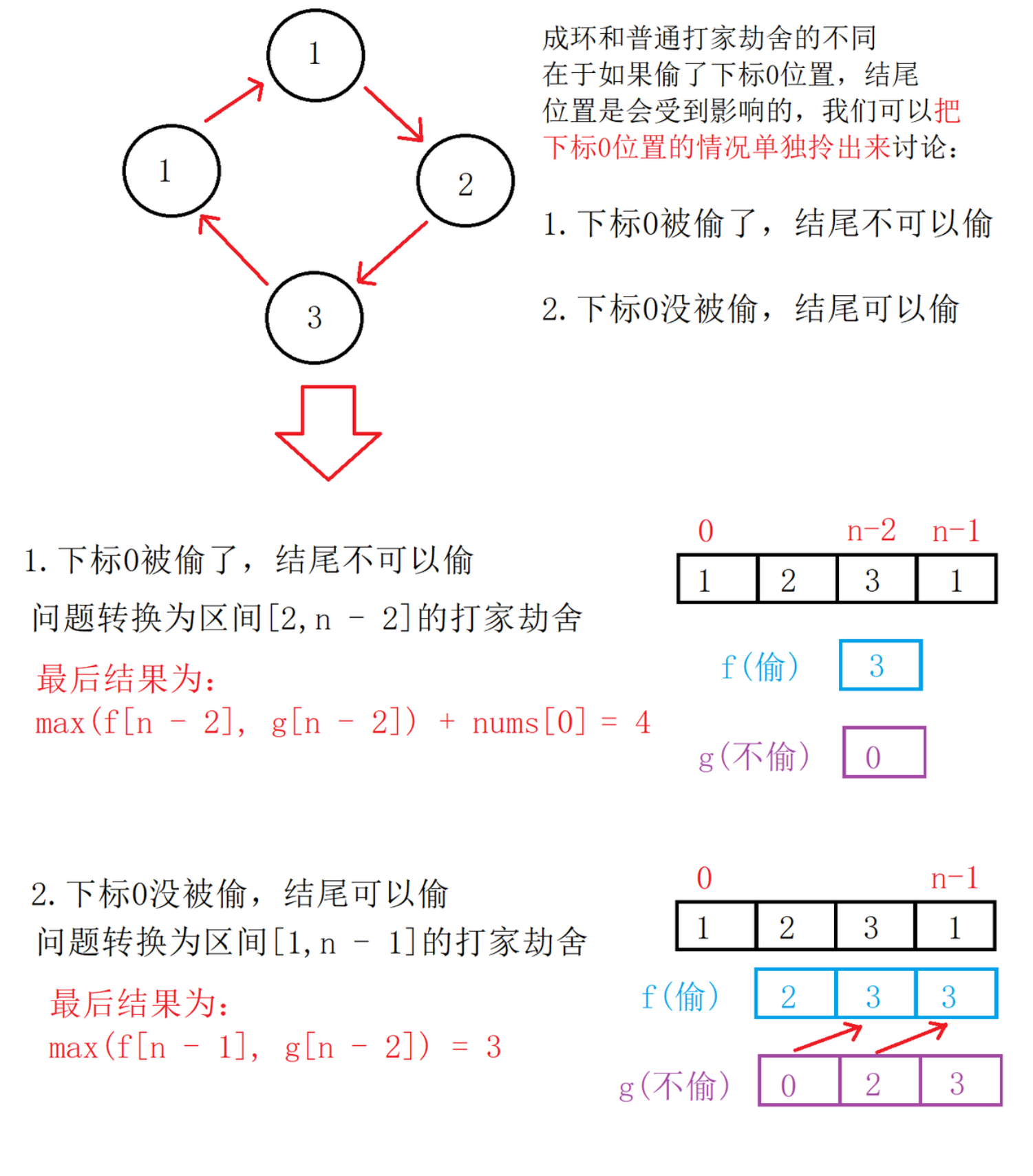
    在这里插入图片描述

  2. 状态转移方程
    和上一道题目一致，状态转移方程为：
    (1) f[i] = g[i - 1] + nums[ i ] (本位置可偷金额)；
    (2) g[i] = max(g[i - 1], f[i - 1])

  3. 初始化
    和上一道题目一致。

  4. 填表顺序
    从左往右。

  5. 返回值
    _rob函数表示指定区间的打家劫舍，返回值为：
    max(nums[0] + _rob(nums, 2, n - 2), _rob(nums, 1, n - 1))。

  • 代码实现
class Solution {
public:
    int _rob(vector<int>& nums, int left,int right) 
    {
        //区间不存在返回0
        if(left > right)
            return 0;
        int n = nums.size();
        
        vector<int> f(n);  //到这个屋子偷的最大金额
        auto g = f; //到这个屋子不偷的最大金额
        f[left] = nums[left];

        for(int i = left + 1; i <= right; i++)
        {
            f[i] = g[i - 1] + nums[i];
            g[i] = max(f[i - 1],g[i - 1]);
        }
        return max(f[right],g[right]);
    }
    int rob(vector<int>& nums) 
    {
        int n = nums.size();
        return max(nums[0] + _rob(nums, 2, n - 2), _rob(nums, 1, n - 1));
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26

3.粉刷房子（中等）

链接：粉刷房子

  • 题目描述
    在这里插入图片描述

  • 做题步骤

  1. 状态表示
    依据经验和题目要求，我们可以把状态定义为把第i号房子粉刷成j颜色的最小花费。
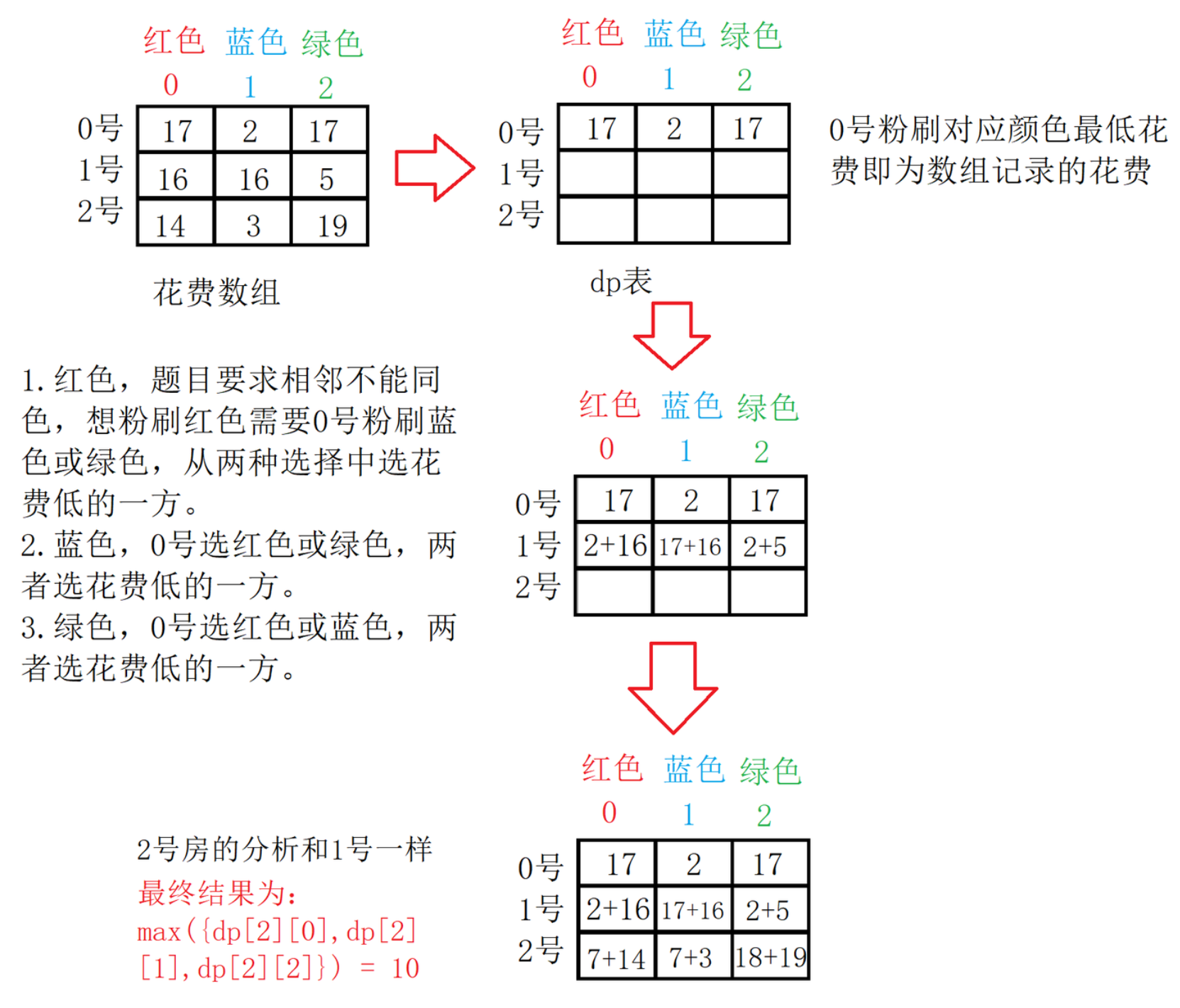
    在这里插入图片描述

  2. 状态转移方程
    状态转移方程为(0是红色、1是蓝色、2是绿色)：
    (1)dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + cost[i][0]（花费）
    (2)dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + cost[i][1]
    (3)dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + cost[i][2]

  3. 初始化
    为了保证填表不越界，我们要初始化第一行的值，但是那样太麻烦了，我们可以多开一行并初始化0，这样就不用单独处理第一行了。（注意和cost数组的下标对应关系）

  4. 填表顺序
    从上往下，每一行从左往右。

5.返回值
依据状态表示，假设最后的房子是i号，返回值为min({dp[n][0], dp[n][1], dp[n][2]})。

  • 代码实现
class Solution {
public:
    int minCost(vector<vector<int>>& costs)
    {
        int n = costs.size();
        //dp[i][j]表示第i号房子粉刷成j颜色的最低花费
        //其中0表示红色，1表示蓝色，2表示绿色
        vector<vector<int>> dp(n + 1, vector<int>(3));
        //空间多开一行并初始化0，不用单独处理第一行

        for (int i = 1; i < n + 1; i++)
        {
            dp[i][0] = costs[i - 1][0] + min(dp[i - 1][1], dp[i - 1][2]);
            dp[i][1] = costs[i - 1][1] + min(dp[i - 1][0], dp[i - 1][2]);
            dp[i][2] = costs[i - 1][2] + min(dp[i - 1][0], dp[i - 1][1]);
        }
        return min({dp[n][0], dp[n][1], dp[n][2]});
        //时间复杂度：O(N)
        //空间复杂度：O(N)
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21

4.删除并获得点数（中等）

链接：删除并获得点数

  • 题目描述
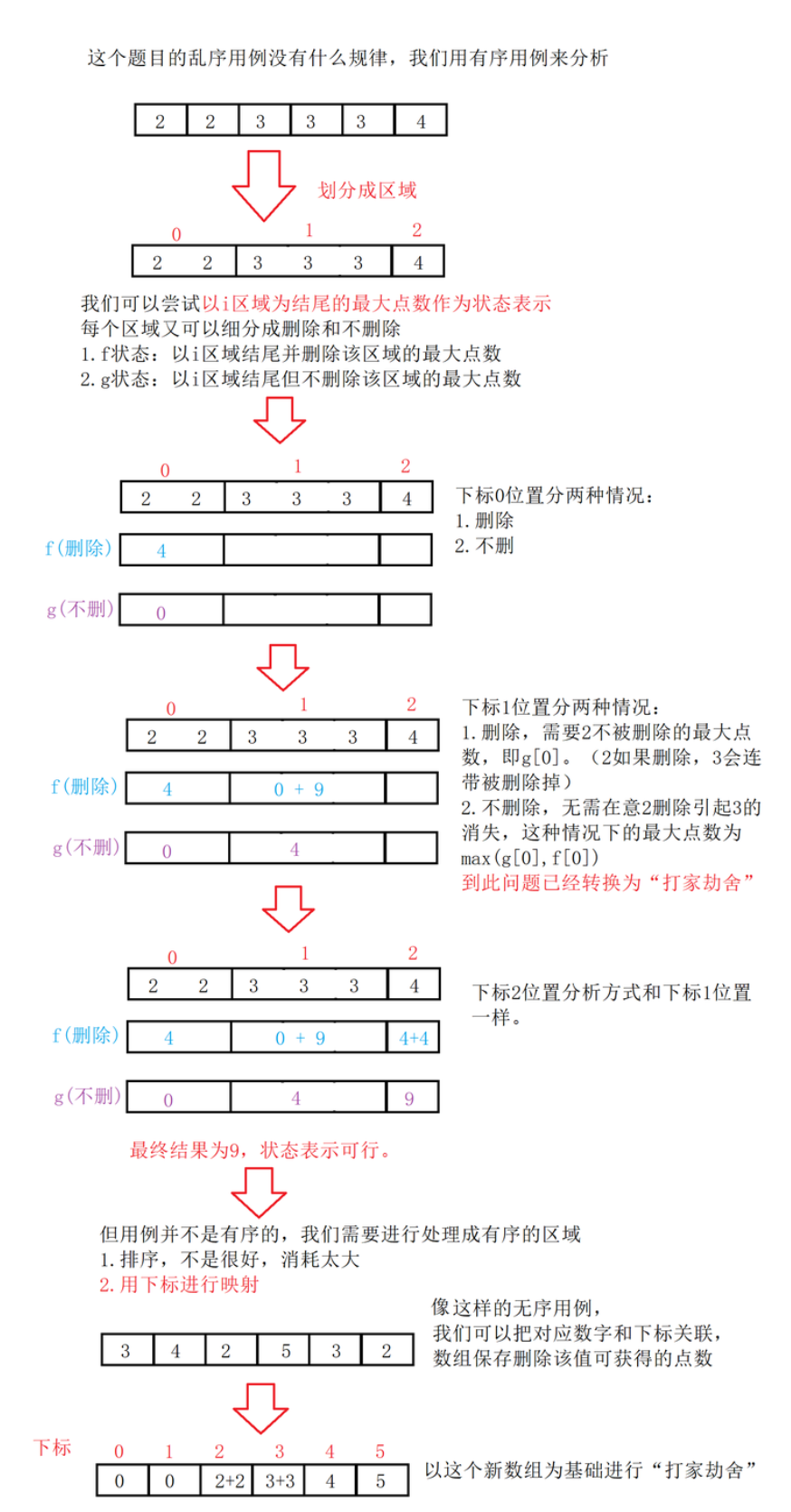
    在这里插入图片描述

  • 做题步骤

  1. 状态表示
    在这里插入图片描述

  2. 状态转移方程
    这个题就是变形的“打家劫舍”，转移方程一致：
    (1) f[i] = g[i - 1] + v[ i ] (删除本位置可得点数)；
    (2) g[i] = max(g[i - 1], f[i - 1])

  3. 初始化
    数组转化完成后dp表不需要处理。

  4. 填表顺序
    从左往右。

  5. 返回值
    返回值为max(f[N - 1],g[N - 1])

  • 代码实现
class Solution {
public:
    int deleteAndEarn(vector<int>& nums)
    {
        int n = nums.size();
    
        //创建数组进行映射
        //题目中1 <= nums[i] <= 10000
        const int N = 10001;
        int v[N] = {0};
        for(auto val : nums)
            v[val] += val;

        //“打家劫舍”
        vector<int> f(N); //f[i]表示以i区域为结尾并且删除本区域的最大点数
        auto g = f;  //g[i]表示以i区域为结尾但不删除本区域的最大点数
        for (int i = 1; i < N; i++)
        {
            f[i] = g[i - 1] + v[i];
            g[i] = max(f[i - 1], g[i - 1]);
        }
        
        return max(f[N - 1],g[N - 1]);
        //时间复杂度：O(N)
        //空间复杂度：O(1)
    }
};


//上面的写法简洁一些，但无论数据量多少都会遍历10000次
//可以记录数组的最大、最小值，来加快速度
// class Solution {
// public:
//     int deleteAndEarn(vector<int>& nums)
//     {
//         int n = nums.size();
//         vector<int> v(10001);
//         //先遍历一次
//         int _max = nums[0];
//         int _min = nums[0];
//         for (int i = 0; i < n; i++)
//         {
//             v[nums[i]] += nums[i];
//             _max = max(_max, nums[i]);
//             _min = min(_min, nums[i]);
//         }

//         vector<int> f(10001);
//         auto g = f;
//         for (int i = _min; i <= _max; i++)
//         {
//             f[i] = g[i - 1] + v[i];
//             g[i] = max(f[i - 1], g[i - 1]);
//         }
        
//         return max(f[_max],g[_max]);
//     }
// };

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58

5.买卖股票的最佳时期含⼿续费（中等）

链接：买卖股票的最佳时期含⼿续费

  • 题目描述
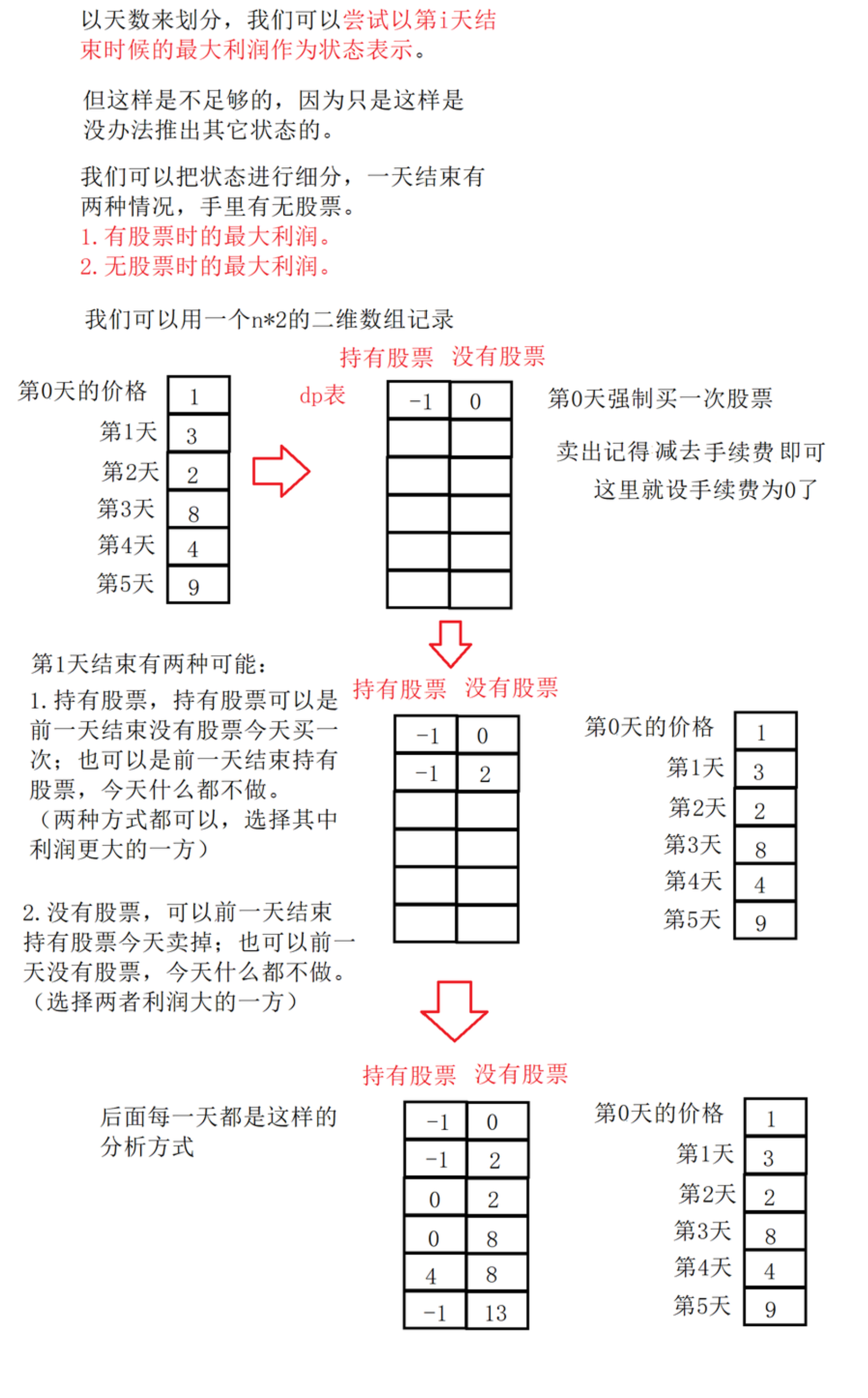
    在这里插入图片描述

  • 做题步骤

  1. 状态表示
    在这里插入图片描述

dp[i][j]：第i天结束时处于j状态的最大利润。

  1. 状态转移方程，0表示结束有股票，1表示结束没有股票，fee是手续费，prices[i]表示第i天的股票价格
    (1)dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])
    (2)dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee)

  2. 初始化
    初始化第0天状态即可，dp[0][0] -= prices[0];。

  3. 填表顺序
    从上到下。

  4. 返回值
    返回值为：max(dp[n - 1][1], dp[n - 1][0])。

  • 代码实现
class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) 
    {
        int n = prices.size();
        //dp[i][j]:第i天结束处于j状态的最大利润
        vector<vector<int>> dp(n, vector<int>(2));
        //这种解法买入还是卖出交手续费都一样(反正买入了一定会卖出)
        dp[0][0] -= prices[0];

        for(int i = 1; i < n; i++)
        {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        }
        return max(dp[n - 1][1], dp[n - 1][0]);
        //时间复杂度：O(N)
        //空间复杂度：O(N)
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20

6.买卖股票的最佳时机含冷冻期（中等）

链接：买卖股票的最佳时机含冷冻期

  • 题目描述
    在这里插入图片描述

  • 做题步骤

  1. 状态表示
    在这里插入图片描述

  2. 状态转移方程
    0是买入（有股票）、1是可交易、2是冷冻，prices[i]表示第i天的股票价格，状态转移方程为：
    (1)dp[i][0] = max(dp[i - 1][1] - prices[i], dp[i - 1][0])
    (2)dp[i][1] = max(dp[i - 1][2], dp[i - 1][1])
    (3)dp[i][2] = dp[i - 1][0] + prices[i]

  3. 初始化
    当前天的三种状态需要前一天的状态，所以初始化dp表的第一行
    dp[0][0]：想该天结束后处于买入状态，必须把股票买了，dp[0][0] = -prices[i]；
    dp[0][1]：什么都不干，dp[0][1] = 0；
    dp[0][2]：想该天结束处于冷冻，在同一天买入和卖出，dp[0][2] = 0；

  4. 填表顺序
    从上到下。

  5. 返回值
    最大值应该手中没有股票，假设数组有n个元素，最大值为max(dp[n - 1][1], dp[n - 1][ 2 ])。

  • 代码实现
class Solution {
public:
    int maxProfit(vector<int>& prices) 
    {
        int n = prices.size();
        //dp[i][j]：第i天结束后处于j状态时的最大利润
        vector<vector<int>> dp(n, vector<int>(3));
        //初始化
        dp[0][0] -= prices[0];

        for(int i = 1; i < n; i++)
        {
            dp[i][0] = max(dp[i - 1][1] - prices[i], dp[i - 1][0]);
            dp[i][1] = max(dp[i - 1][2], dp[i - 1][1]);
            dp[i][2] = dp[i - 1][0] + prices[i];
        }
        
        return max(dp[n - 1][2],dp[n - 1][1]);
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20

7.买卖股票的最佳时机III（困难）

链接：买卖股票的最佳时机III

  • 题目描述
    在这里插入图片描述

  • 做题步骤

  1. 状态表示
    在这里插入图片描述

  2. 状态转移方程
    由前面的分析可知，状态转移方程为：
    (1)f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i])
    (2)if(j >= 1) g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i])
      else g[i][j] = g[i - 1][j]

  3. 初始化
    需要i = 0的状态，初始化第一行。
    (1)处于第一行的时候只有f[0][0]和g[0][0]存在，f[0][0] = -prices[0]，g[0][0] = 0。
    (2)为了避免不存在的状态干扰取max值，我们把不存在的状态统一初始化为 INT_MIN / 2。（INT_MIN会越界，尽可能小就行）

  4. 填表顺序
    从上往下填每一列，从左往右填每一行。

  5. 返回值
    返回最后一行的最大值即可。

  • 代码实现
class Solution {
public:
    //可能会越界,取INT_MIN的一半
    const int INF = INT_MIN / 2;
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        //dp[i][j]表示在第i天结束后完成j次交易，处于""状态下的最大利润
        vector<vector<int>> f(n, vector<int>(3, INF));  //买入
        auto g = f;  //可交易
        //初始化
        f[0][0] = -prices[0];
        g[0][0] = 0;

        for (int i = 1; i < n; i++)
        {
            for(int j = 0; j < 3; j++)
            {
                f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                //j == 0的时候前置状态f[i - 1][j - 1]不存在
                if(j >= 1)
                    g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
            }                                    
        }
        return max({g[n - 1][0], g[n - 1][1], g[n - 1][2]});
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27

8.买卖股票的最佳时机IV（困难）

这个题目的思考方式和第7题完全一致，大家可以先自己试着做一下。
链接：买卖股票的最佳时机IV

  • 代码实现
class Solution {
public:
    const int INF = INT_MIN / 2;
    int maxProfit(int k, vector<int>& prices) 
    {           
        int n = prices.size();
        //n天最多完成n / 2次交易，k不能超过这个值
        k = min(k, n / 2);
        //买入
        //dp[i][j]表示在第i天结束后完成j次交易，处于""状态下的最大利润
        vector<vector<int>> f(n, vector<int>(k + 1, INF));
        //卖出
        auto g = f;
        //初始化(先买再说)
        f[0][0] = -prices[0];
        g[0][0] = 0;

        for (int i = 1; i < n; i++)
        {
            for(int j = 0; j <= k; j++)
            {
                f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if(j >= 1)
                    g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
            }                                    
        }
        int ret = g[n - 1][0];
        //把利润最大的那个找出来
        for(int j = 1; j <= k; j++)
        {
            ret = max(ret, g[n - 1][j]);
        }
        return ret;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/474588
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号