翻译: 什么是ChatGPT 通过图形化的方式来理解 Transformer 架构 深度学习二

合集 ChatGPT 通过图形化的方式来理解 Transformer 架构

1. 翻译: 什么是ChatGPT 通过图形化的方式来理解 Transformer 架构 深度学习一
2. 翻译: 什么是ChatGPT 通过图形化的方式来理解 Transformer 架构 深度学习二
3. 翻译: 什么是ChatGPT 通过图形化的方式来理解 Transformer 架构 深度学习三
4. 翻译: 什么是ChatGPT 通过图形化的方式来理解 Transformer 架构 深度学习四
5. 翻译: 什么是ChatGPT 通过图形化的方式来理解 Transformer 架构 深度学习五
6. 翻译: 什么是ChatGPT 通过图形化的方式来理解 Transformer 架构 深度学习六
   

在本章中,我们将深入探讨

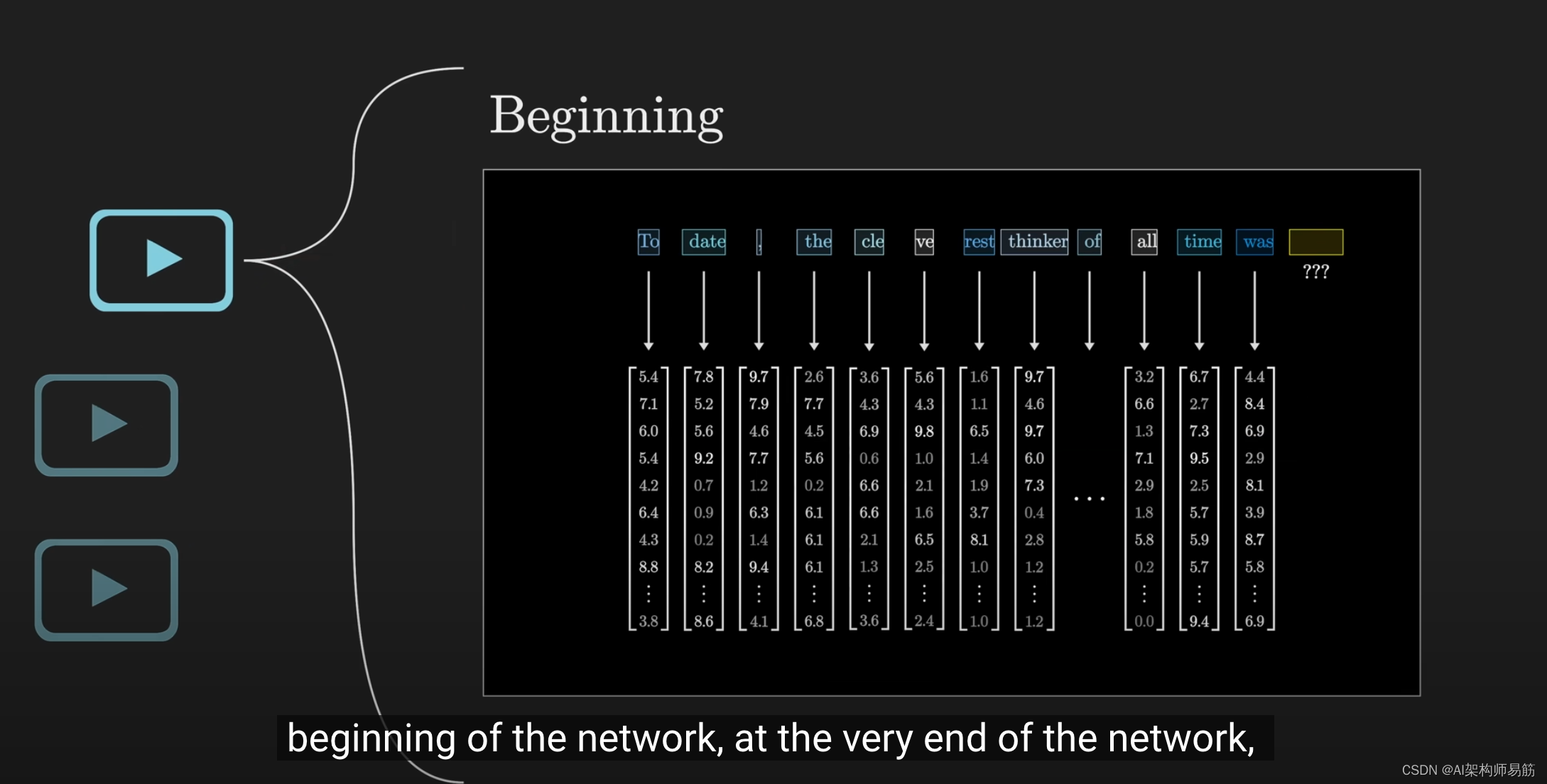
网络的开始和

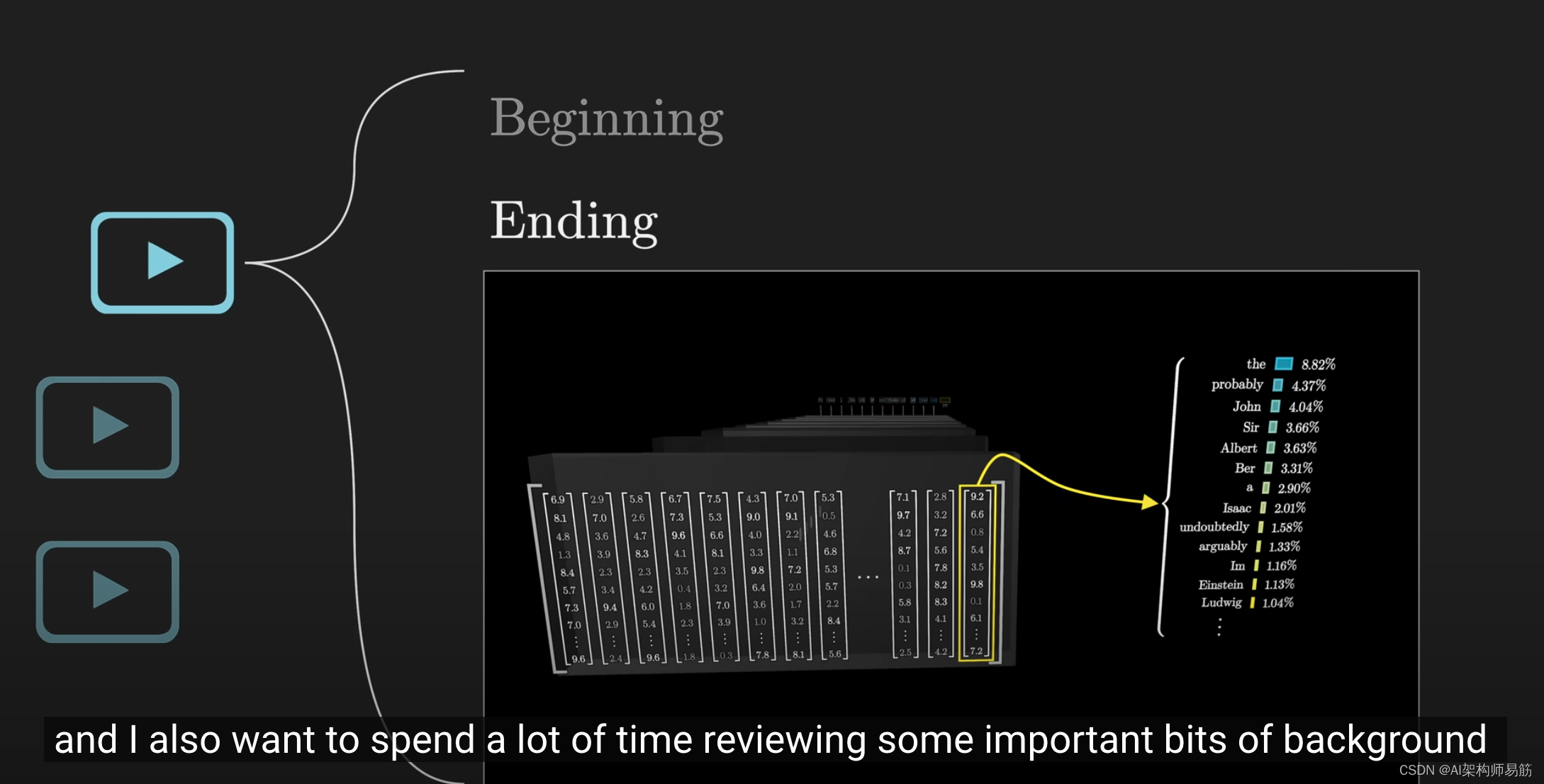
结束阶段发生的情况,

我将花大量时间回顾一些重要的背景知识,这些知识是熟悉Transformer的机器学习工程师的基础知识。

如果你已经熟悉背景知识,迫不及待地想了解更多,你可以跳到下一节,重点将放在Transformer的核心部分——注意力模块上。

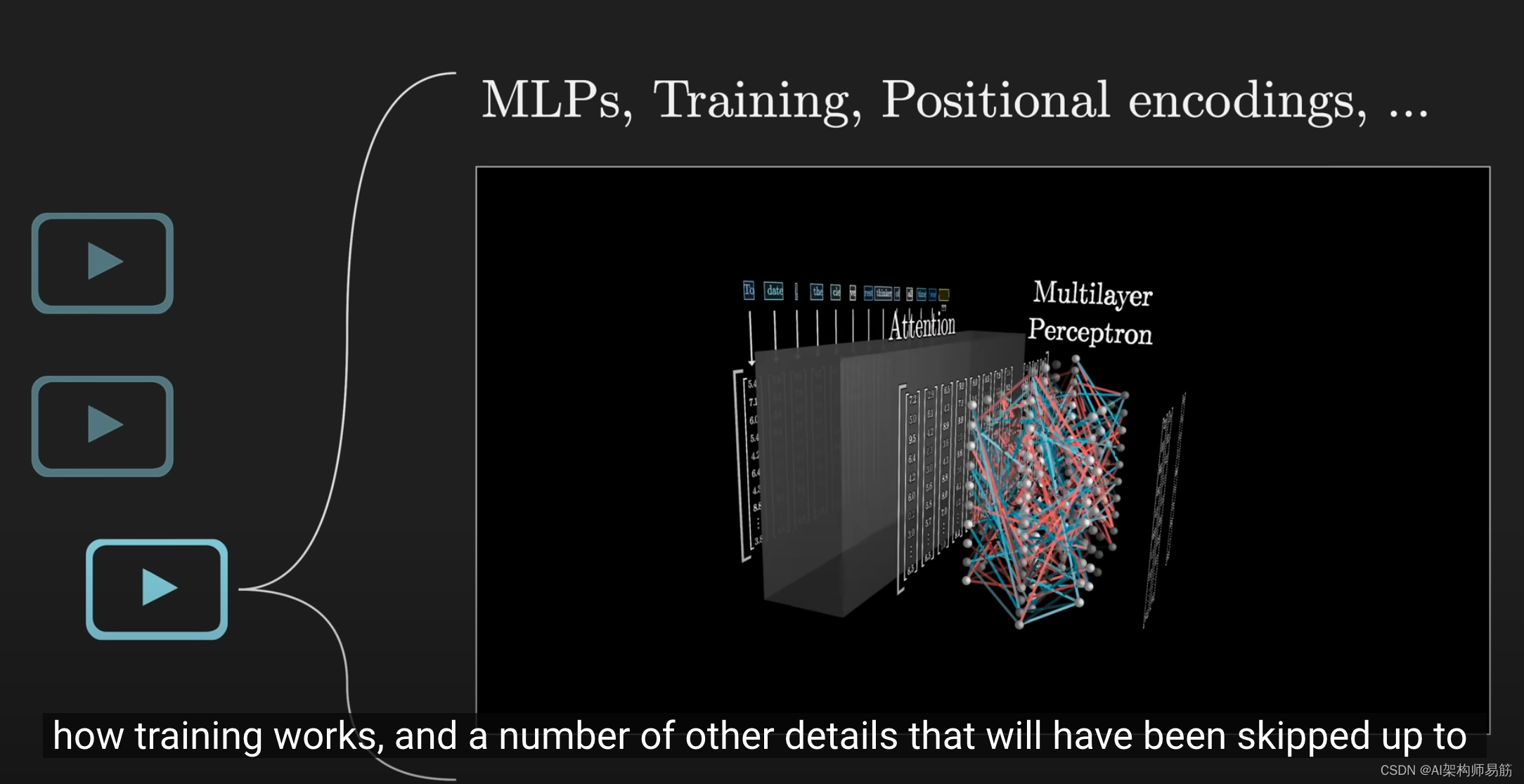
之后,我将更详细地介绍多层感知器模块、训练过程以及之前省略的一些其他细节。

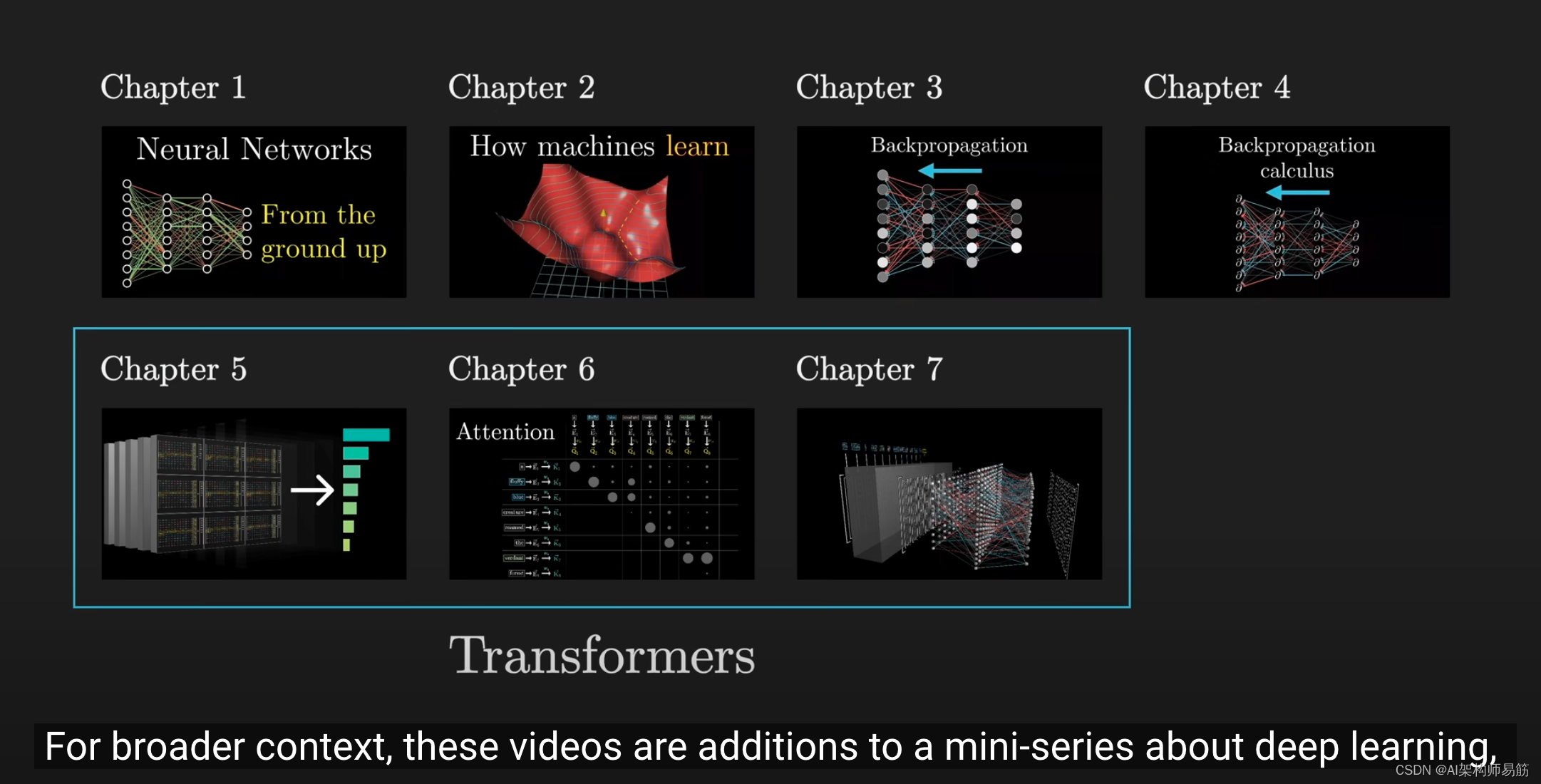
对于背景信息,这些视频是对我们深度学习课程系列的补充,你不一定要按顺序观看,

但在深入研究Transformer之前,我认为确保我们对深度学习的基本概念和架构有共同的理解很重要。

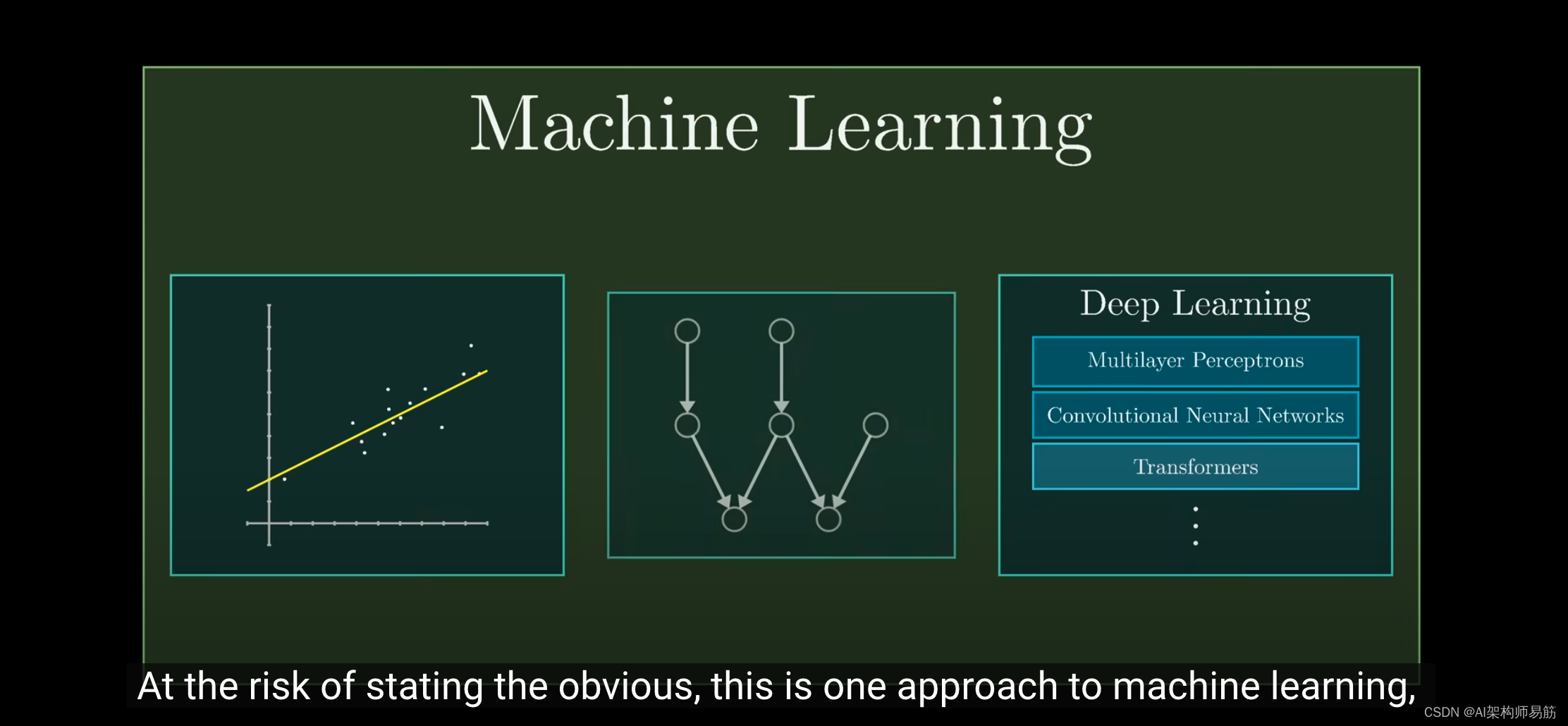
这里要明确的是,

机器学习是一种使用数据来指导模型行为模式的方法。

具体来说,你可能需要一个函数,它接受一个图像,输出一个词描述,

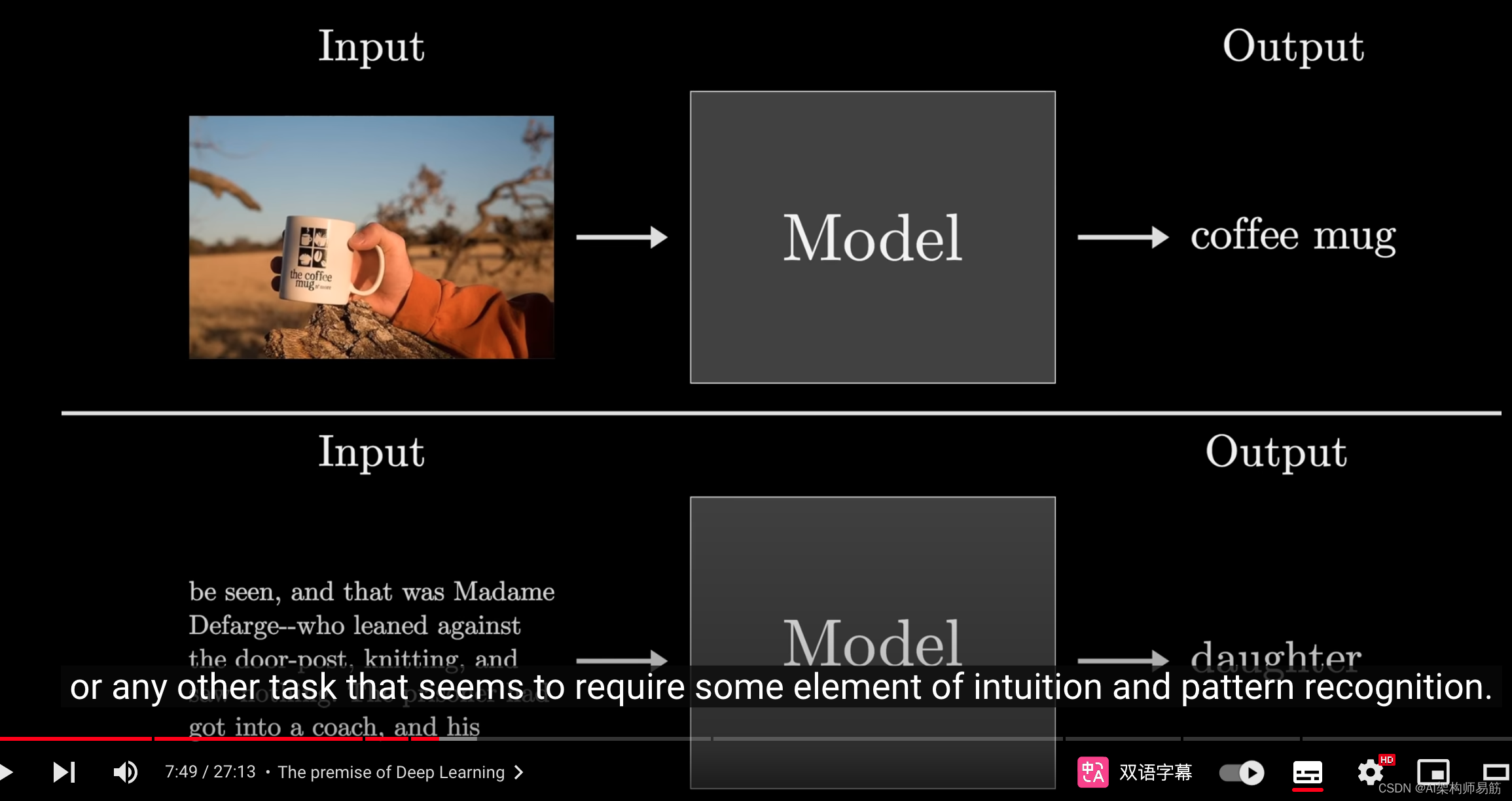
或者为给定的文本预测下一个词,

或者其他需要直觉和模式识别的任务,

虽然我们现在已经习惯了,但机器学习的核心思想是,我们不再试图编写固定的程序来完成这些任务,这是人们在人工智能最早期会做的事情。

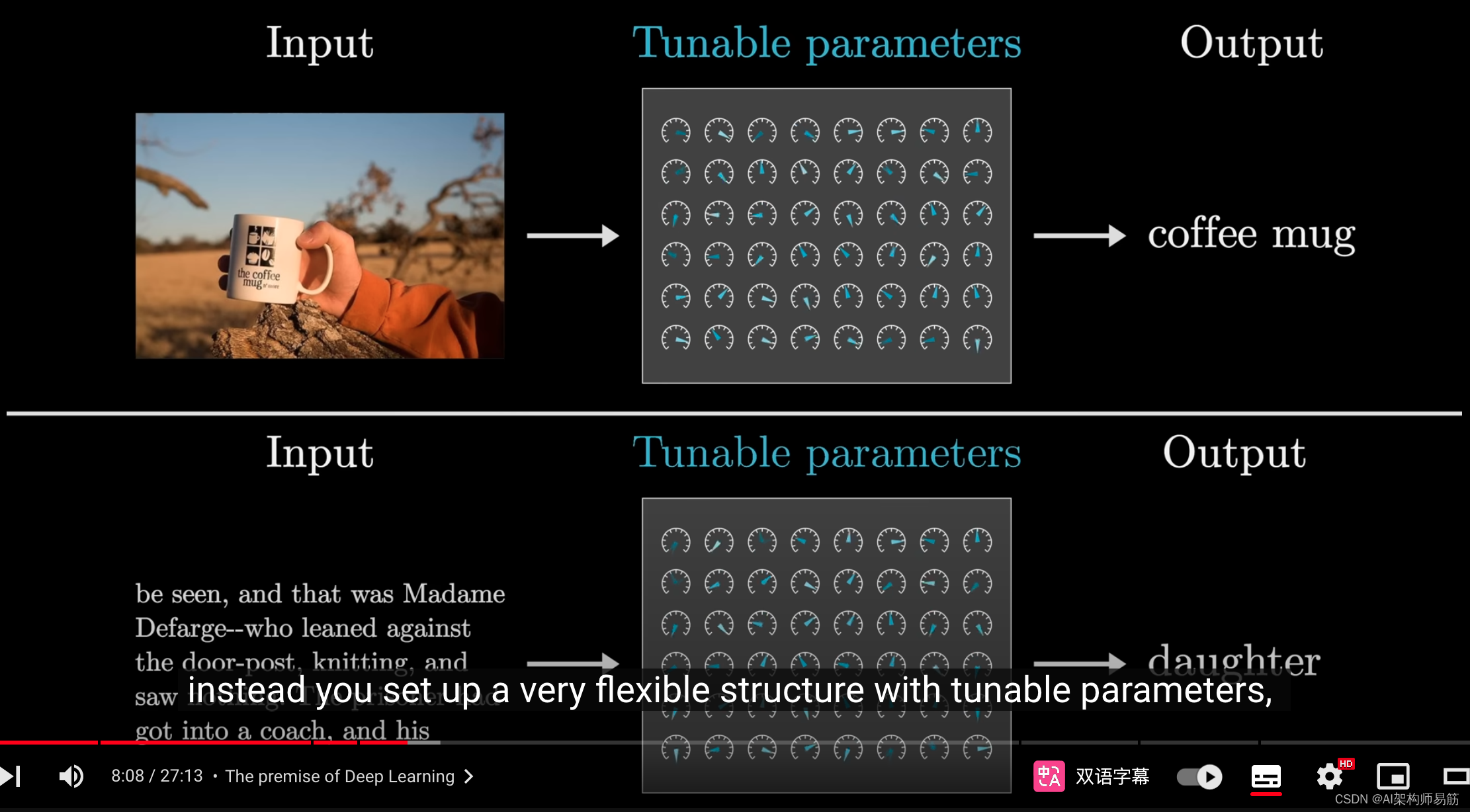
相反,构建一个具有可调参数的灵活结构,就像一系列旋钮和调节器,

然后通过学习大量实例输入和期望输出来调整和微调参数值,从而模拟这种直觉行为。

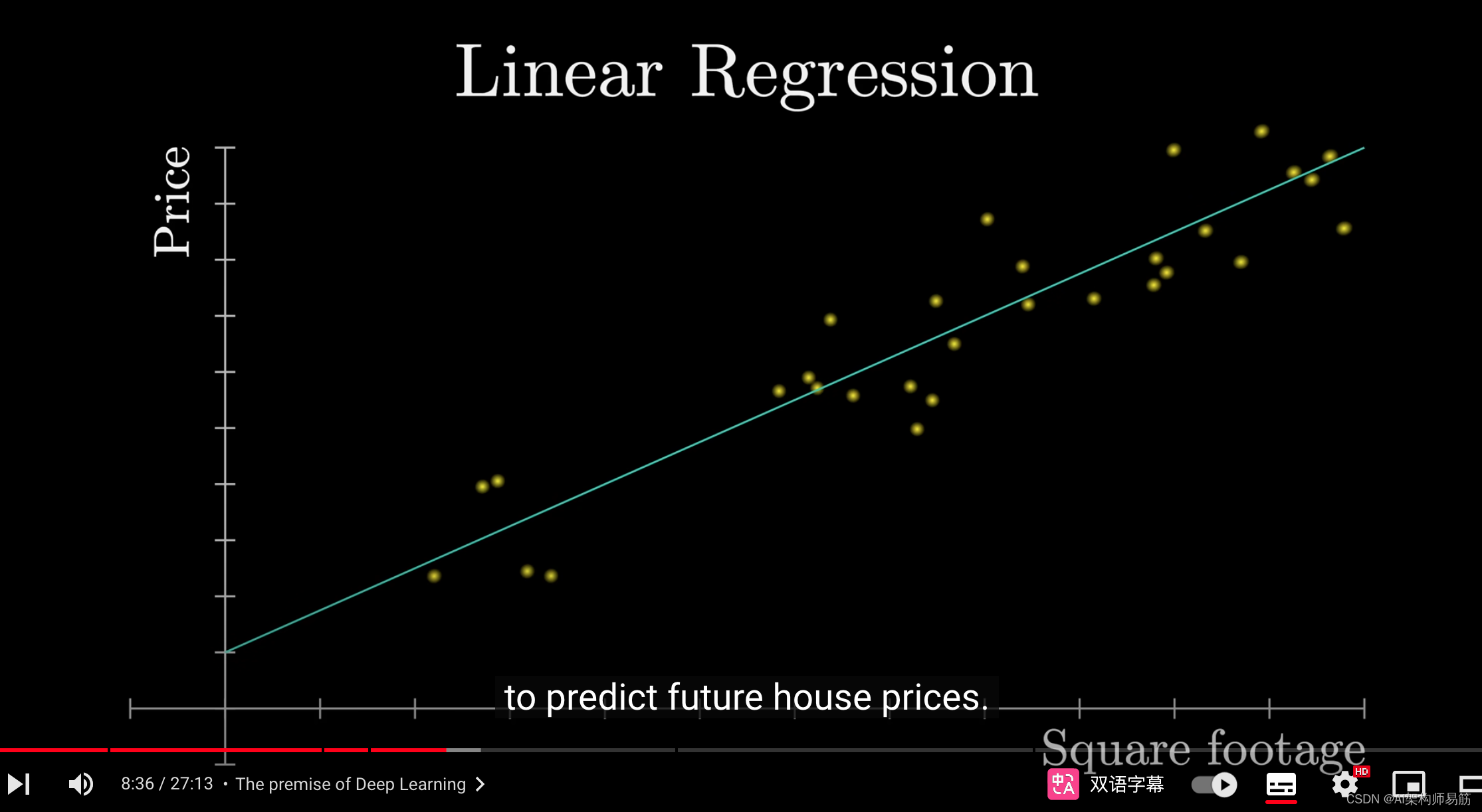
例如,可能最直观的入门机器学习模型是线性回归,你将输入和输出视为单个数字,如房屋面积和价格,你要做的就是找到最适合这些数字的直线。这用于预测未来的房价。

这条线由两个连续的参数组成,即斜率和y截距。

线性回归的目标是确定这些参数以尽可能接近地匹配数据。

不用说,深度学习模型会更加复杂。

例如,GPT-3有1750亿个参数,而不仅仅是两个。

然而,重要的是要注意,你不能简单地构建一个具有许多参数的大型模型就能有效工作,这样做可能会导致模型严重过拟合训练数据,或者极难训练。

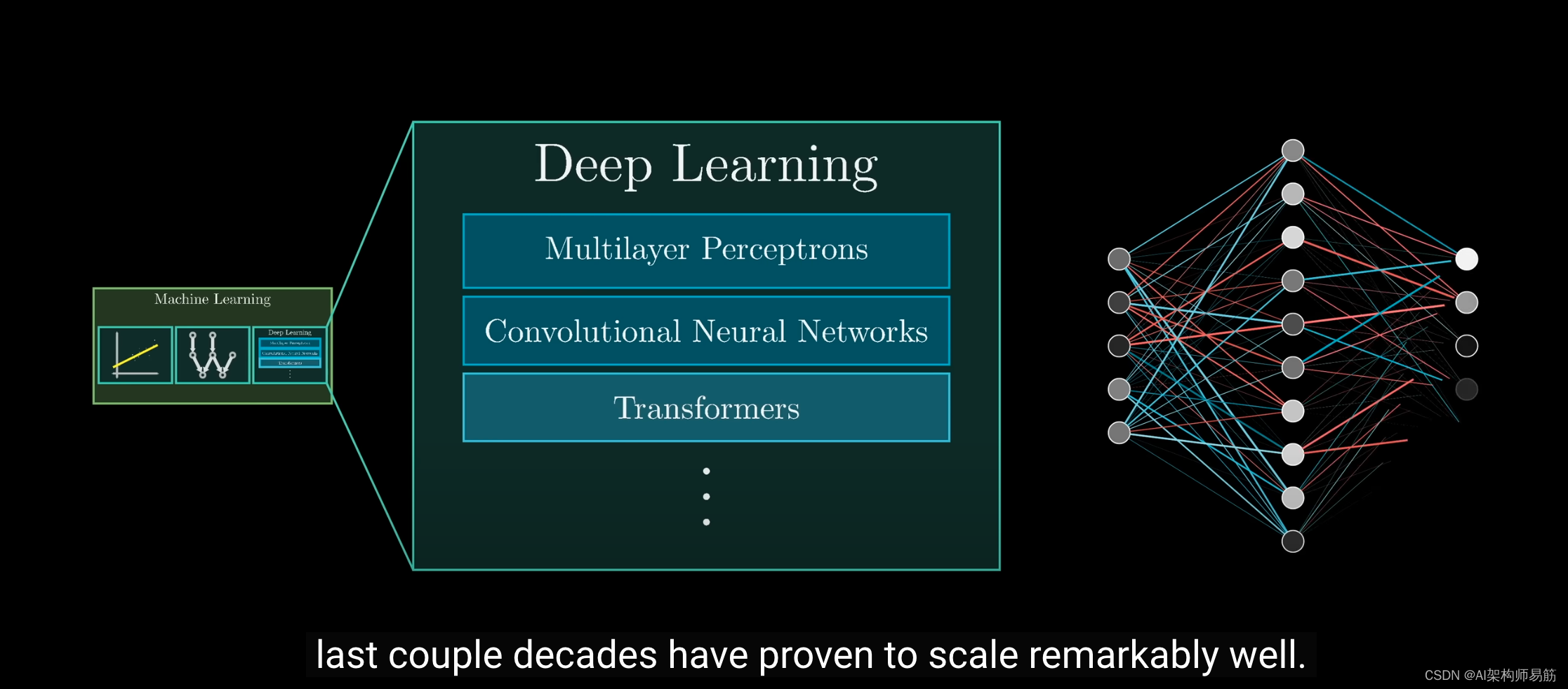
深度学习包括一系列在过去几十年中已被证明在扩展能力方面表现出色的模型类别。

它们成功的关键在于,它们都使用相同的训练算法:反向传播,我们在前面的章节中已经介绍过。

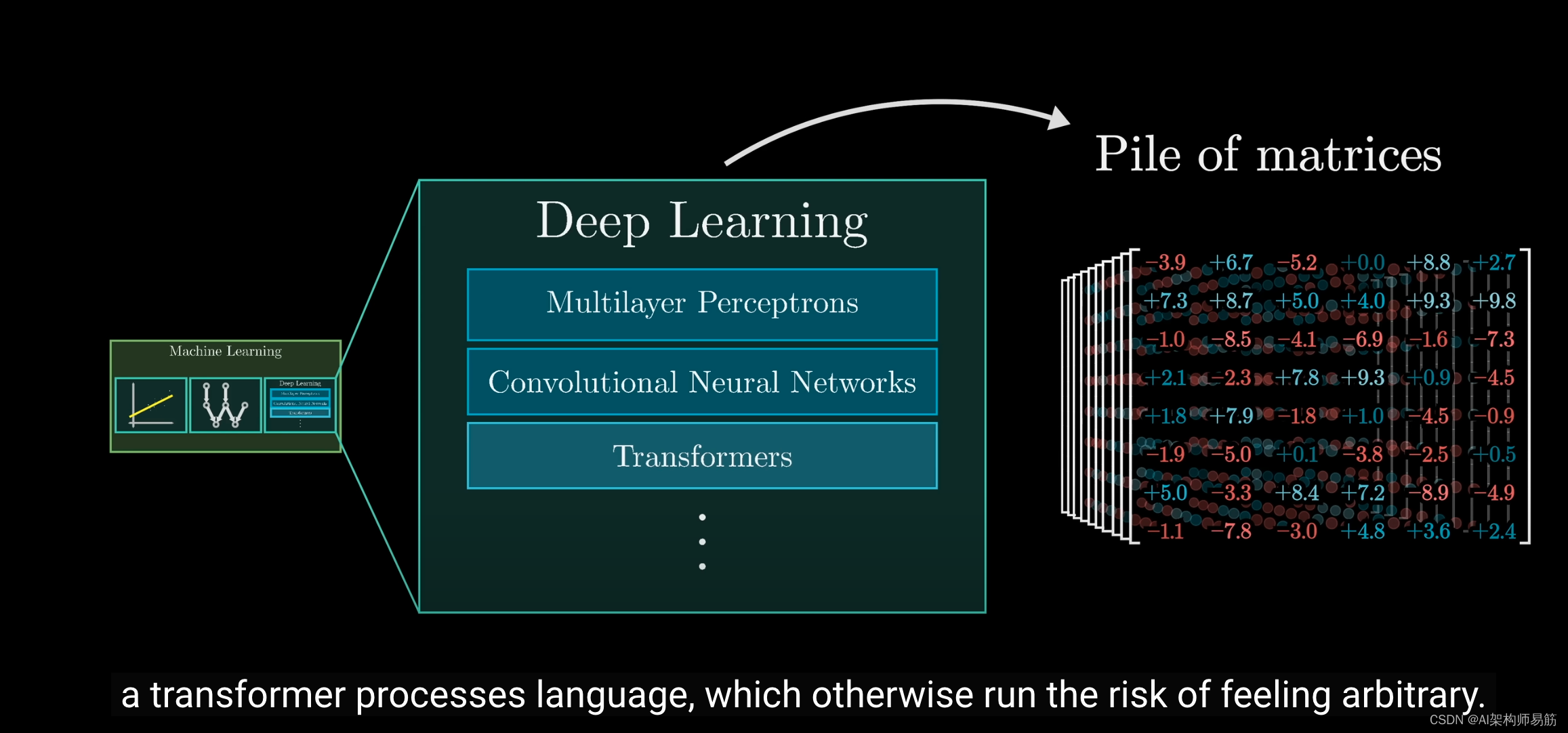
你需要理解的是,为了让这个训练算法在大规模应用中很好地工作,模型必须遵循特定的结构。

如果你了解这个结构的一些知识,你将更好地理解Transformer如何处理语言以及其背后的逻辑,否则某些设计选择可能看起来有点随意。

首先,无论你要构建什么样的模型,输入必须是一个实数数组。

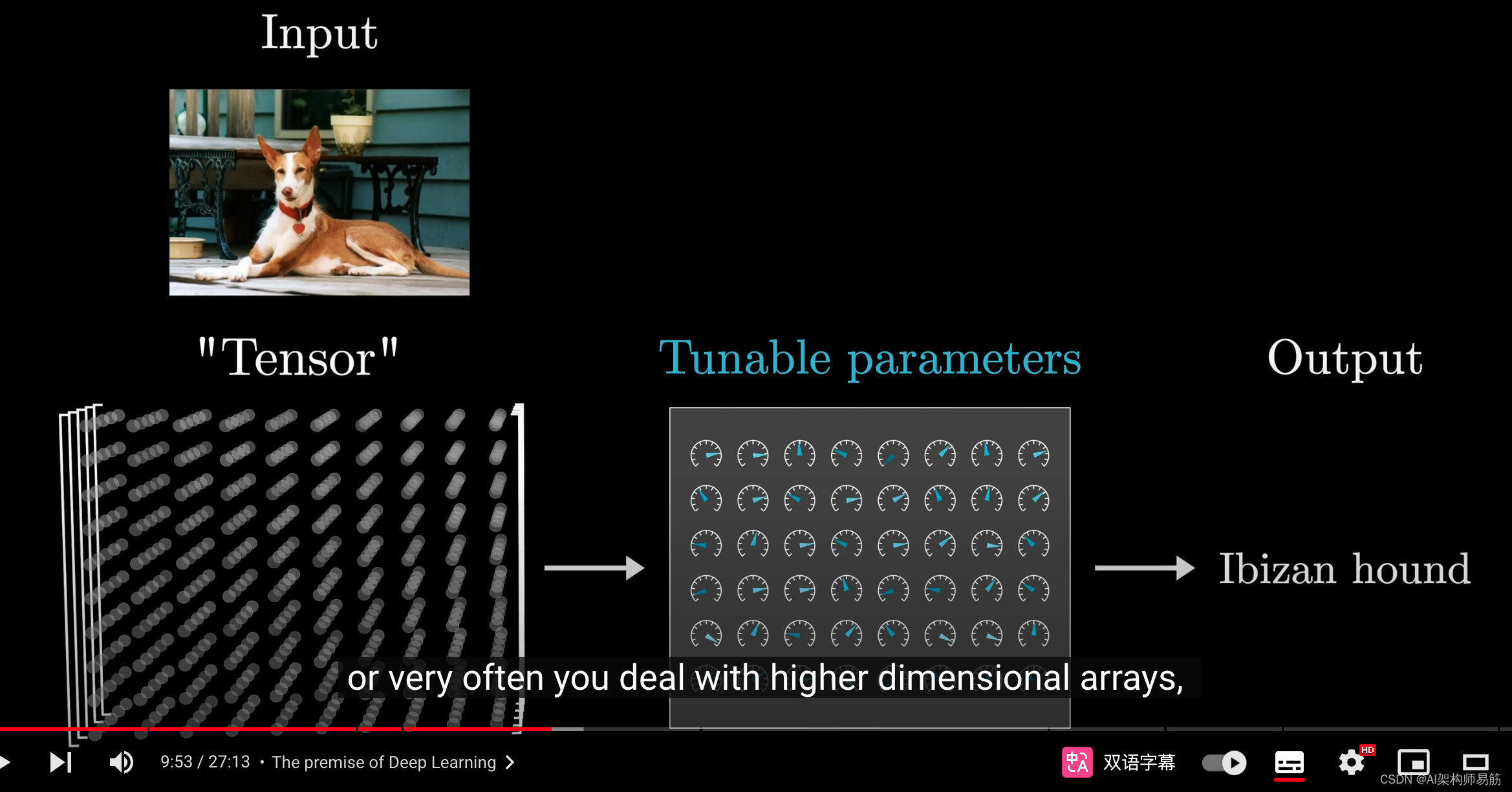
这可能只是一个数字列表,或者是一个二维数组,或者更常见的是一个更高维的数组,这个通用术语叫做张量(tensor)。

这些输入通常通过多个不同的层逐步转换,每一层形成一个实数数组,直到最后一层,你可以将其视为输出层。

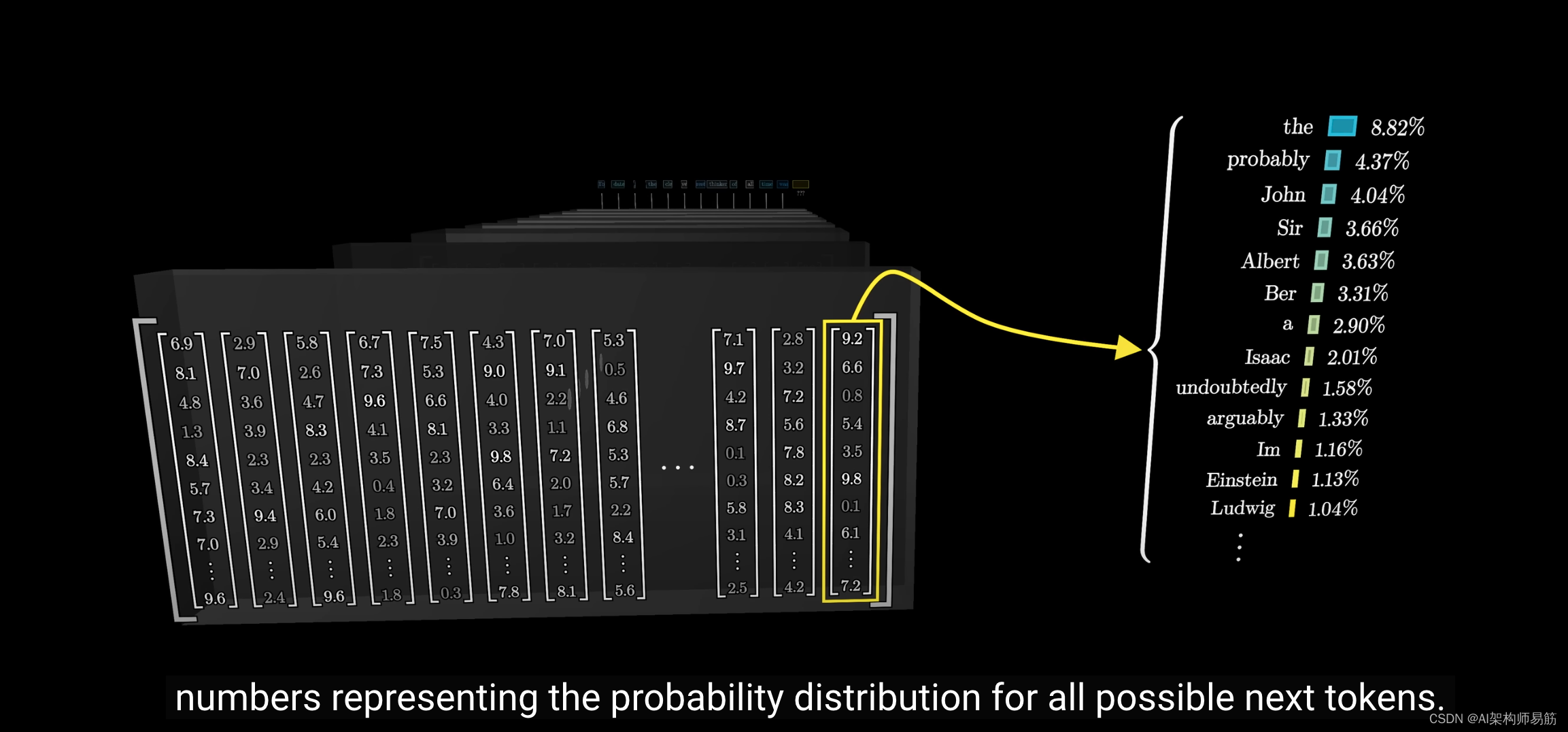
例如,我们文本处理模型的最终输出层是一个数字列表,表示所有可能的下一个词的概率分布。

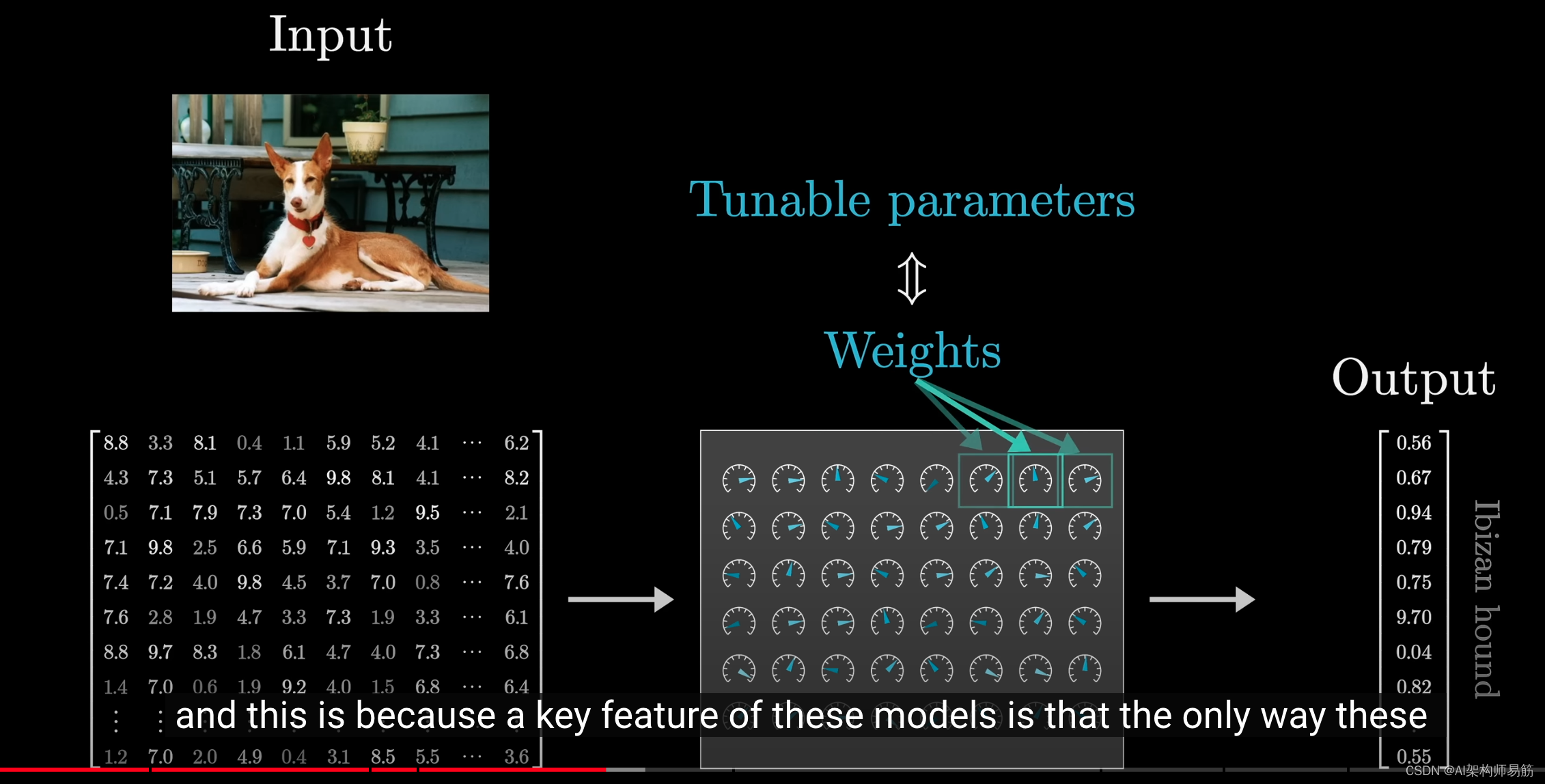
在深度学习领域,这些模型的参数通常被称为权重(weight)。

这样称呼的原因是,这些模型的核心特征之一是,这些参数与正在处理的数据交互的唯一方式是通过加权求和。

虽然模型中穿插了一些非线性函数,但它们并不依赖于这些参数。

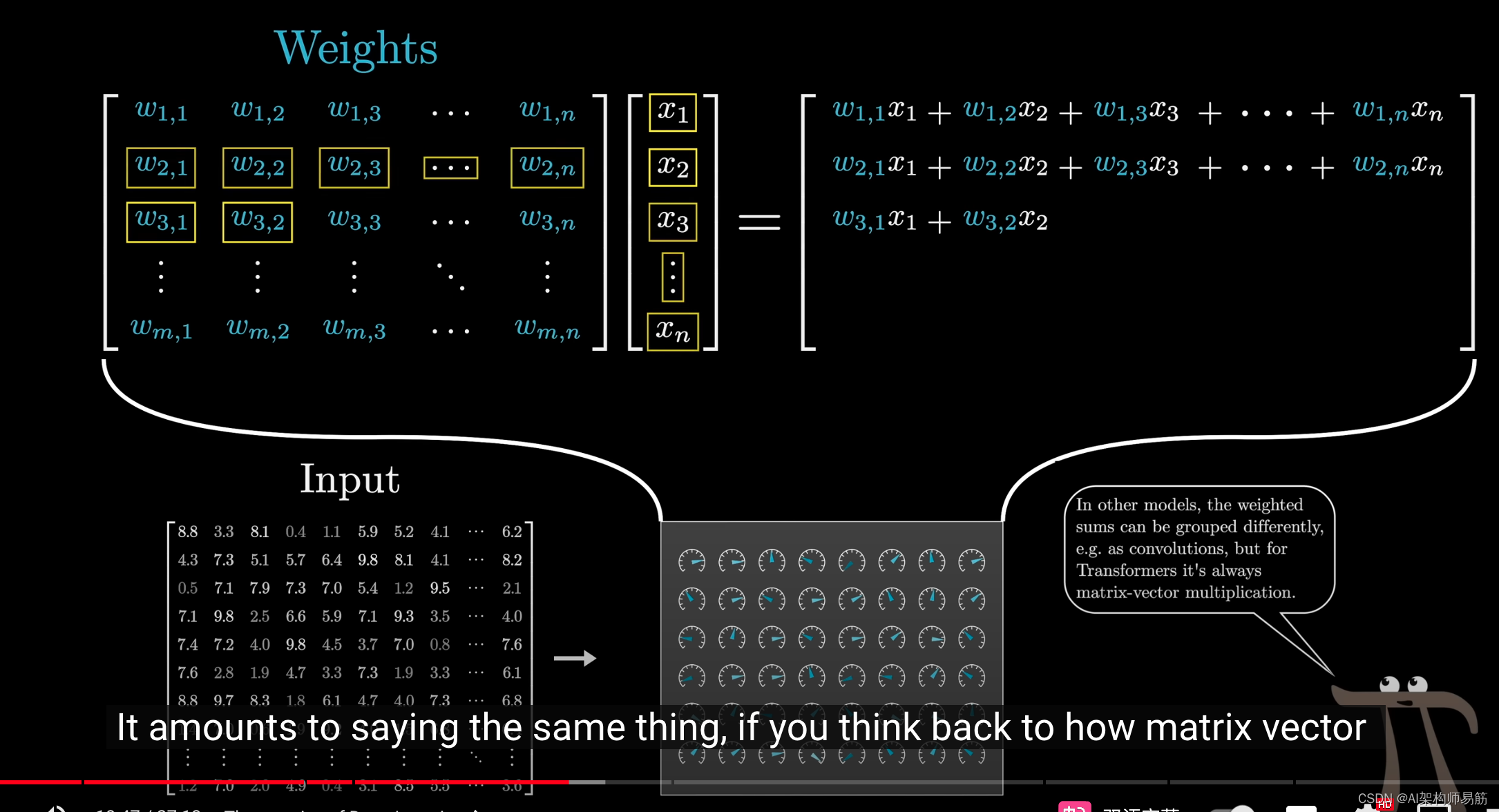
总的来说,我们不会直接以裸露的形式看到这些权重,而是看到它们被封装为矩阵向量乘积的不同部分。

如果你回想一下矩阵向量乘法的工作原理,输出的每个部分都像是权重的总和。

一种更直观的方式是将这些可调参数填充的矩阵,

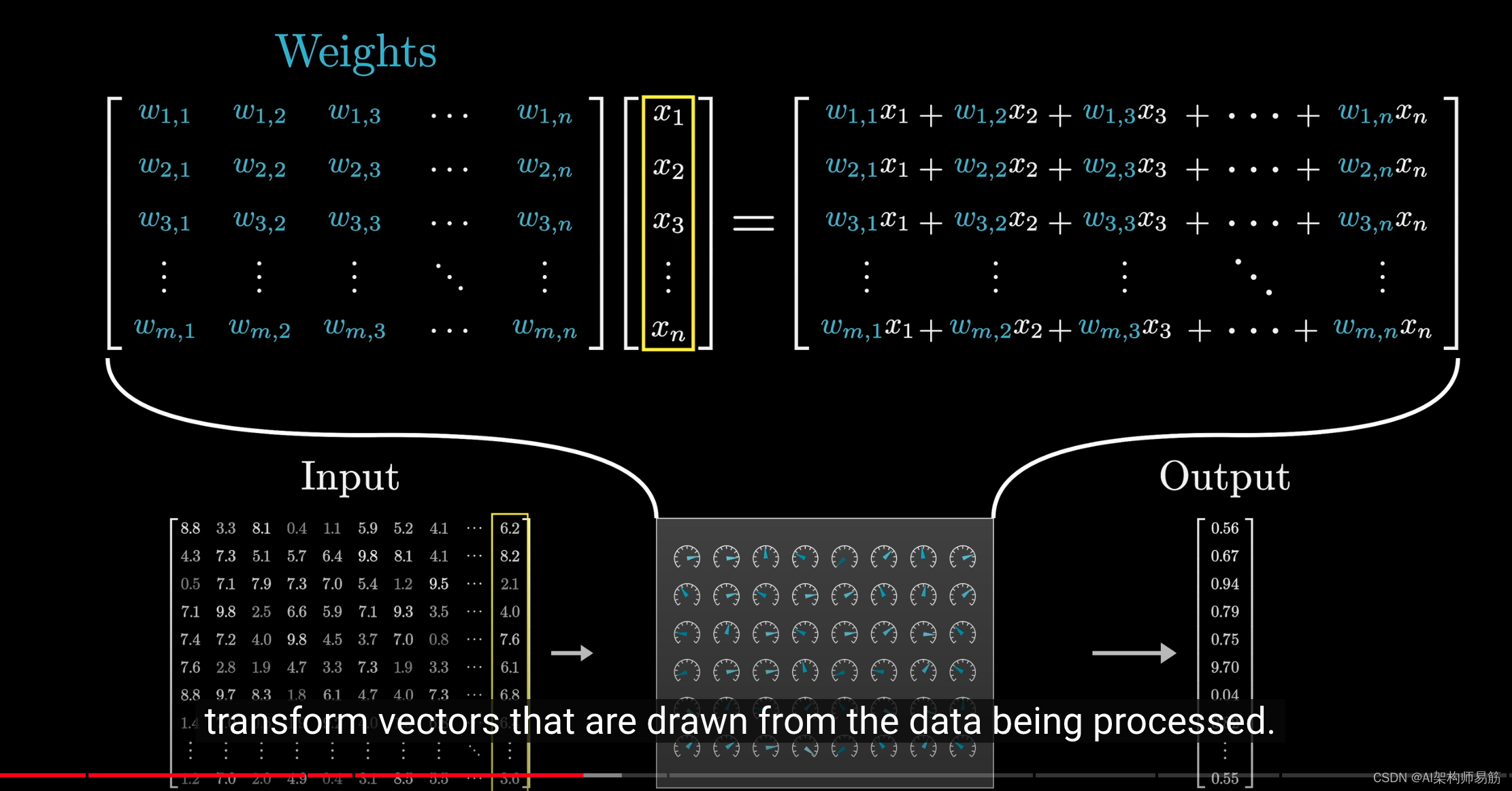
视为对正在处理的数据进行向量变换的工具。

参考

https://youtu.be/wjZofJX0v4M?si=DujTHghH5dYM3KpZ