【深大算法设计与分析-实验二-分治法求最近点对】_算法设计与分析python空间最小距离点对分治算法

---

实验要求与内容

 掌握分治法思想，学会最近点对问题求解方法。

1. 对于平面上给定的N个点，给出所有点对的最短距离，即，输入是平面上的N个点，输出是N点中具有最短距离的两点。

2. 要求随机生成N个点的平面坐标，应用蛮力法编程计算出所有点对的最短距离。

3. 要求随机生成N个点的平面坐标，应用分治法编程计算出所有点对的最短距离。

4. 分别对N=100000—1000000，统计算法运行时间，比较理论效率与实测效率的差异，同时对蛮力法和分治法的算法效率进行分析和比较。

5. 如果能将算法执行过程利用图形界面输出，可获加分。

二．实验步骤与结果

1）数据准备：利用python的随机数库生成（10，100，1000，10000，100000，1000000）规模的不重复的随机整型数，然后将这些整型数乘上一个大小在（0.8，1.2）随机的浮点数得到点集合的横坐标，以同样的方式得到点集的中坐标，将这些点放入到point数组中。

for i in [10, 100, 1000, 10000, 100000, 1000000]:
    point_x = random.sample(range(1, i + 1), i)
    point_y = random.sample(range(1, i + 1), i)
    point = []
    for j in range(i):
        radio_x = round(random.uniform(0.8, 1.2), 3)
        radio_y = round(random.uniform(0.9, 1.1), 3)
        temp = [float(point_x[j]) * radio_x, float(point_y[j]) * radio_y]
        point.append(temp)

---

2）暴力穷举法

        暴力法既是遍历所有的点对，然后直接输出查找的最小距离。

        a. 算法流程

        

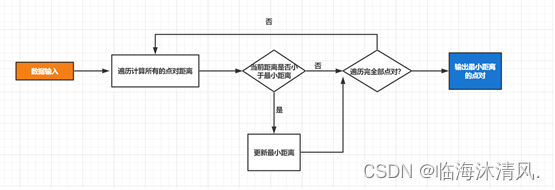
        b. 时间复杂度分析

        遍历所有的点对，则可以将点对集看成是一张无向完全图，查找最小的距离既是找图中最短的边。因为无向完全图的变数是n(n-1)/2，所以计算次数既是n(n-1)/2，所以暴力法的时间复杂度为O(n²)。

3）分治法

        遍历所有的点对，则可以将点对集看成是一张无向完全图，查找最小的距离既是找图中最短的边。因为无向完全图的变数是n(n-1)/2，所以计算次数既是n(n-1)/2，所以暴力法的时间复杂度为O(n²)。

a. 算法思路：

1.将点对沿着x轴方向进行排序

    2.判断n的大小：

        N = 1时返回999999；

        N = 2时直接返回这两个点对的距离；

        N > 2时将点对分成（n/2）的两个部分，重复2的过程

    3.找到子问题的解并将子问题按照y轴方向排好序

    4.找到横坐标范围在[point[mid].x–min_dist, point[mid].x+min_dist]的所有点(异侧点)

    5.将4中的点与六个基准点比较找到最小的距离

b. 算法流程

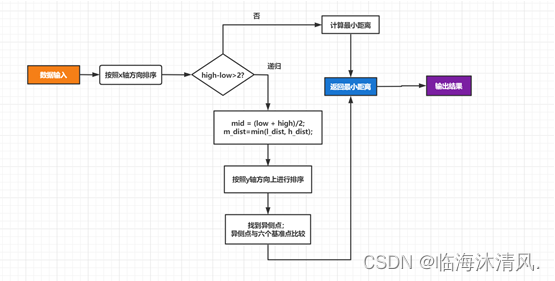
c. 流程解释：

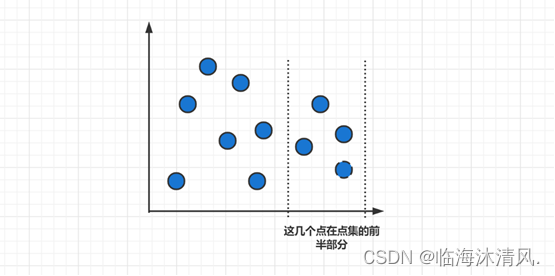
    1.为什么要对点对的横坐标进行排序？

    因为我们点对是随机生成的并且我们的分治法是采用二分法将点对分成两个子部份的，如果没有对点对进行x轴方向的排序，有50%的概率我们点对集合中前半部分的点在x轴的后半部分，如下方图4所示），这样的话我们就不能对点对集合进行正确的划分。

     2. n的规模不同时计算方法不同

 点数大于2时，将其划分成点数较少的情况再来计算。

3.点集划分后的情况：

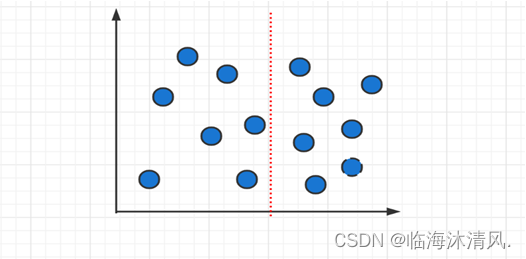
假设点集中拥有最小距离的两个点为p1,p2，则他们的分布情况有三种：

    P1,p2都在左侧：

    P1,p2都在右侧；

    P1,p2在异侧

    对于前面两种情况，我们可以在递归过程中的规模判断时解决，所以我们重点讨论第三种情况。我们在直线L两边分别扩展d，得到边界区域Y，Y’是区域Y中的点按照y坐标值排序后得到的点集。

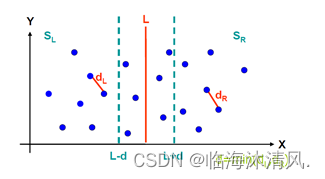
 为什么要对y进行排序？ 因为在这个矩形区域内我们要判断最小距离的点对是否存在，我们采取的方法是与六个基准点进行比较，如果不排序的话我们无法优化查找过程，实践复杂度达不到我们想要的效果。

4. 分界区域内点对的查找

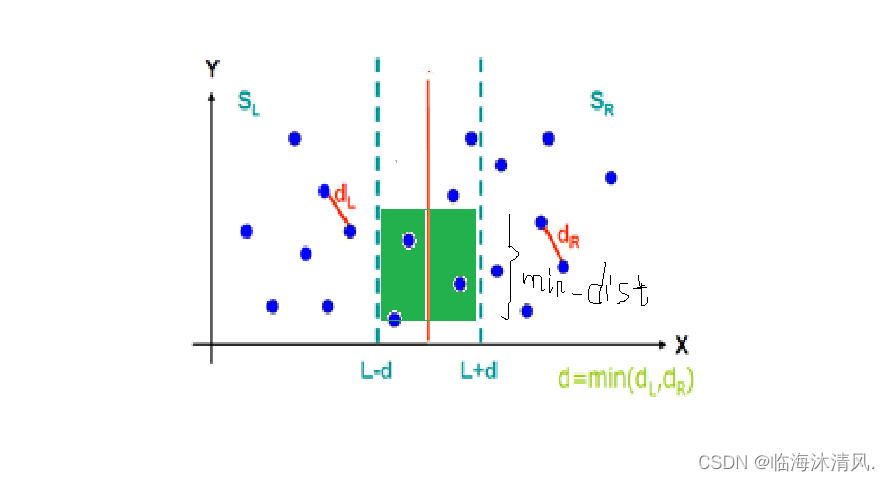
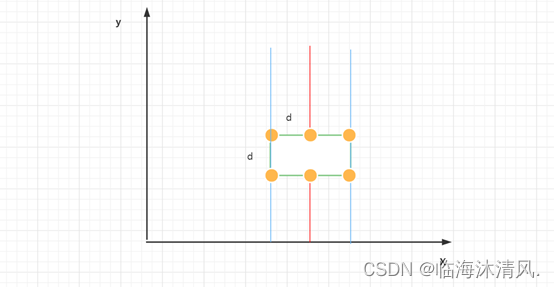
    我们对Y`区域内的点进行检擦，因为该区域内的点已经按Y方向排好了序，如果区域内存在比当前最小距离海小的点对，那么他一定位于绿色的方框内。因为绿色矩形的高为min_dist，如果最小的距离的点对不位于里面，则他们之间的距离一定大于min_dist，所以他们就一定不是最小的距离点对。然后对于图8中绿色区域内的左半边矩形，因为SL中所有点之间最小距离为d，依鸽笼原理，该正方形内最多有4个点（如下图）。类似地，SR中也最多有4个点可以位于该d×d的正方形内。又因为两个正方形存在一条边完全重合，故有两个点为同一个点，因此在判断时只需判断每个点与其余6个基准点间距离关系即可。

d. 时间复杂度分析

    1.我们在递归过程中对子问题的点对进行了y方向的排序，我们的排序方法是类似与归并排序，将有序的两个子部分点对合并成一个有序的点对，因此我们可以知道合并操作中比较的交换次数满足

                                                      (high − low) / 2≤ n ≤high − low

所以对于每次规模为n = high – low的合并操作，时间复杂度为O(n)。又因为单个点对6个基准点的枚举操作是O(1),所以n个点的枚举时间为O(n)。

    我们假设程序的总耗时为T(n)，因为我们对x轴进行排序调用的是快速排序，且每层递归调用花费的时间为t(n)，所以

                                      ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​ T(n) = t(n) + O(nlogn)

    又因为

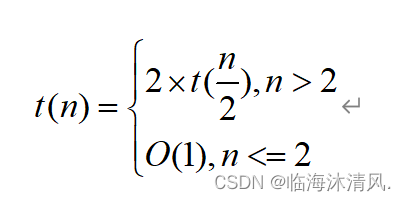
 最终计算得，程序的时间复杂度为 O(nlogn)。

4）算法正确型检验

    在小规模数据上检验算法的正确性。检测用的数据为10组规模为100的随机浮点数

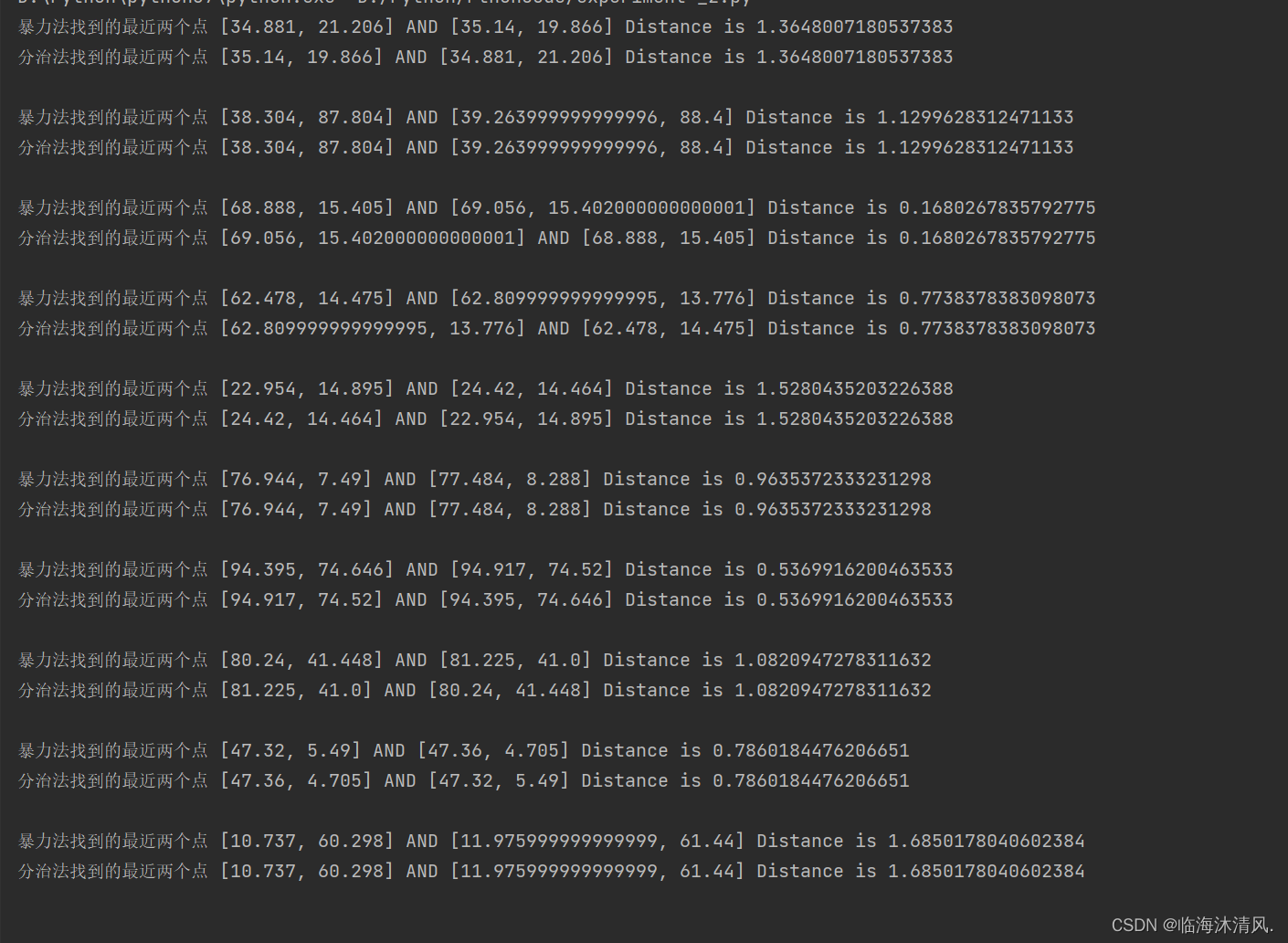
 经过测试，暴力枚举发和分治法的算法正确性达到要求。

5）算法性能分析

    a. 分治法

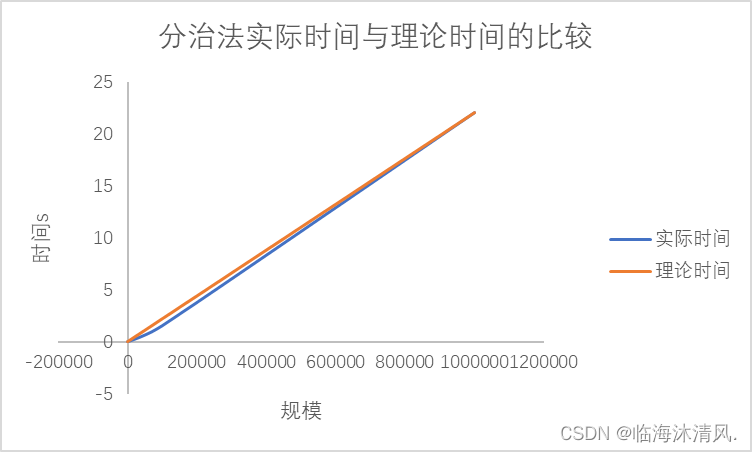
    在实际时间开销与理论时间开销比较中本文选取1000000规模时的实际时间作为基准点

    分治法的算法时间复杂度为O(nlogn)，并且分治法在计算过程中递归调用函数和开辟空间会消耗一定的时间，故当我与1000000规模点对最为基准点时，实际时间与理论实践误差较大。并且图中我们看到，分治法在中小规模数据时求解速度很快；当数据规模较大时理论时间与实际时间的误差更小。

b. 暴力法

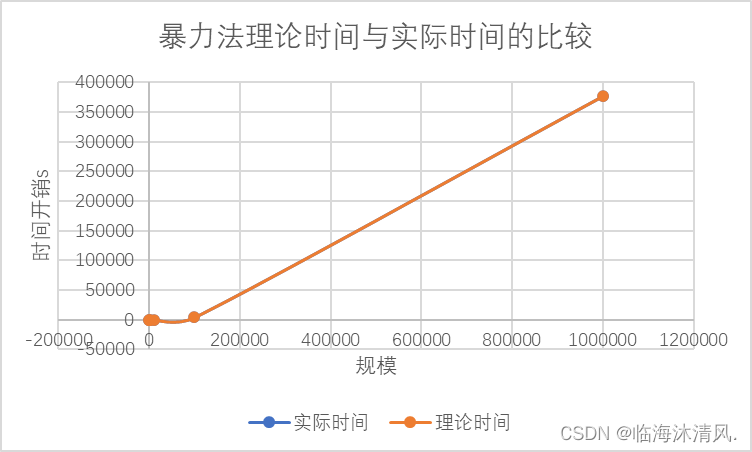
    在实际时间开销与理论时间开销比较中本文选取1000000规模时的实际时间作为基准。

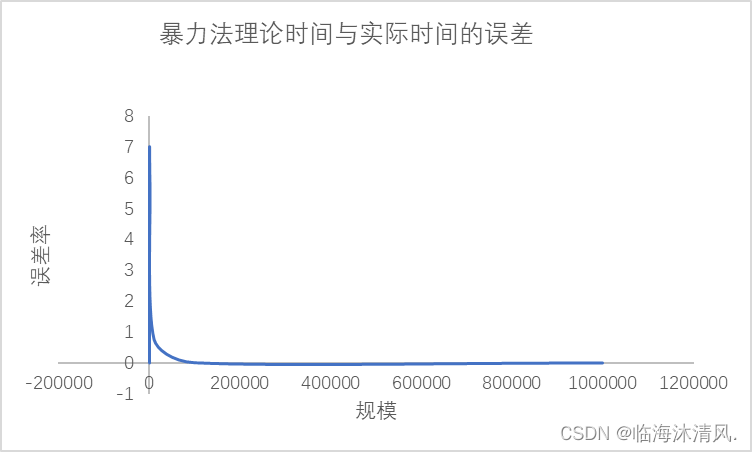
    暴力法的时间复杂度为O(n²)，并且在该算法过程中没有递归、开辟空间等其他时间开销，所以选取1000000规模的数据作为基准点时拟合效果理想。

c. 分治法和暴力法的性能分析

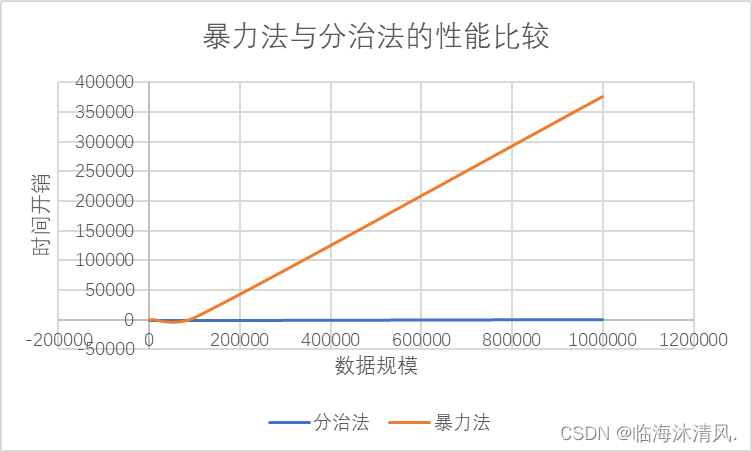
    在图中我们可以看到，在数据规模大于100000时，分治法的性能显著优于暴力法，在数据规模较小（n<100）时暴力法优于分治法。

d. 算法改进

二维平面上两点的距离公式为

                   

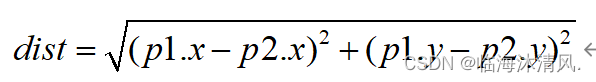
我们可以在比较的过程中先不打dist开方，直接用平方和来比较，最后再把最终结果开方，这样我么可以减少开方的运算次数，降低算法运行时间。

在暴力法中的测试

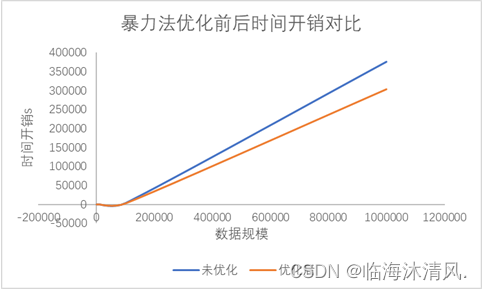
由图中可以看出，优化后暴力法的平均降低20%的时间开销。

---

总结

通过本次实验，了解掌握了分支算法。

代码链接