热门标签
热门文章
- 1通过pycharm创建Django新项目_pycharm创建django app
- 2GitHub的原理及应用详解(一)
- 3word中装订线位置_Word教程:文档”双面打印“全攻略,解决打印难题!
- 4使用SwitchHosts和GitHub520自动更新 github.com的hosts_switchhosts 自动更新google地址
- 5初阶数据结构之双向链表详解
- 6Android Studio 解决编译报错 Could not download aapt2-windows.jar
- 7堆排序
- 8二分查找最坏查找次数_快速入门二分查找
- 9NLP学习笔记(四) Seq2Seq基本介绍_seq2seq模型说的时间步是什么意思
- 10初学者必须弄懂的一些基本FPGA设计概念(1)_fpga 设计
当前位置: article > 正文
Logistic模型
作者:笔触狂放9 | 2024-05-27 04:48:14
赞
踩
logistic模型
文章内容部分参考自:
(9条消息) 数学建模——人口预测模型公有木兮木恋白的博客-CSDN博客数学建模人口预测模型
logistic回归应用指南 - 知乎 (zhihu.com)
一、模型概述

非线性最小二乘估计
- clc, clear
-
- a=textread('data4.txt'); %把原始数据保存在纯文本文件data4.txt中
-
- x=a([2:2:6],:)'; %提出人口数据
-
- x=nonzeros(x); %去掉后面的零,并变成列向量
-
- t=[1790:10:2000]';
-
- t0=t(1); x0=x(1);
-
- fun=@(cs,td)cs(1)./(1+(cs(1)/x0-1)*exp(-cs(2)*(td-t0))); %cs(1)=xm,cs(2)=r
-
- cs=lsqcurvefit(fun,rand(2,1),t(2:end),x(2:end),zeros(2,1))
-
- xhat=fun(cs,[t;2010]) %预测已知年代和2010年的人口

二、logistic回归应用
logistic回归是一种广义的线性回归分析模型,常用于疾病诊断、经济预测等领域,主要用途为寻找危险因素(寻找某一疾病的危险因素)、预测(不同自变量情况下,某病或某种情况的发生概率)和判别(判断某人属于某病或某种情况的概率有多大),在疾控项目中较多涉及寻找危险因素,因此,本文主要以寻找危险因素进行举例说明。
直接用SPSS软件去分析,操作指南见:
logistic回归应用指南 - 知乎 (zhihu.com)
三、人口预测
1、特点
考虑了人口能够承受的最大值
数据出错时拟合的不够好,必须要有正确的数据才能够拟合
数学模型简单,有一定的公式
2、代码实现
原理
Logistic模型认为人口增长有最大值Xm和人口的固有增长率r0。当人口增长到Xm附近,人口将保持这个水准不会有大的变动,数学公式如下
- dx/dt=r0(1-x/Xm)x
- x(0)=x0
x是人口数量,x0是初始人口数量
解这个方程组得到
x=Xm/(1+(Xm/x0-1)exp(-r0t))3、代码
- clc
-
- clear
-
- closeall
-
- x=[97.42102.36105.78 111.16 116.04 121.71 126.26 134.93 141.24 141.89 143.2 147];%常驻老年人口
-
- n=length(x);
-
- t=0:1:n-1;
-
- rk=zeros(1,n);
-
- rk(1)=(-3*x(1)+4*x(2)-x(3))/2;
-
- rk(n)=(x(n-2)-4*x(n-1)+3*x(n))/2;
-
- fori=2:n-1
-
- rk(i)=(x(i+1)-x(i-1))/2;
-
- end
-
- rk=rk./x;
-
- p=polyfit(x,rk,1);
-
- b=p(2);
-
- a=p(1);
-
- r0=b;
-
- xm=-r0/a;
-
- %输出
-
- pnum=zeros(n,1);
-
- fori=0:1:n-1
-
- pnum(i+1)=xm/(1+(xm/x(1)-1)*exp(-r0*i));
-
- end
-
- year1=2008:2019;
-
- plot(year1,pnum,'r--o',year1,x,'k-*')
-
- xlabel('年份')
-
- ylabel('老年人口数量/万人')
-
- legend('预测老年人口数量','实际老年人口数量')

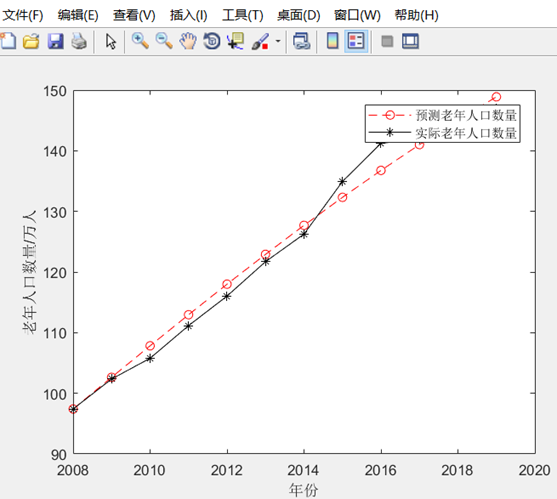
预测
- figure(2)
-
- fnum=zeros(n+16,1);
-
- fori=0:1:n+15
-
- fnum(i+1)=xm/(1+(xm/x(1)-1)*exp(-r0*i));
-
- end
-
- year2=2008:2035;
-
- plot(year2,fnum,'r--o')
-
- xlabel('年份')
-
- ylabel('老年人口数量/万人')
-
- legend('预测老年人口数量')

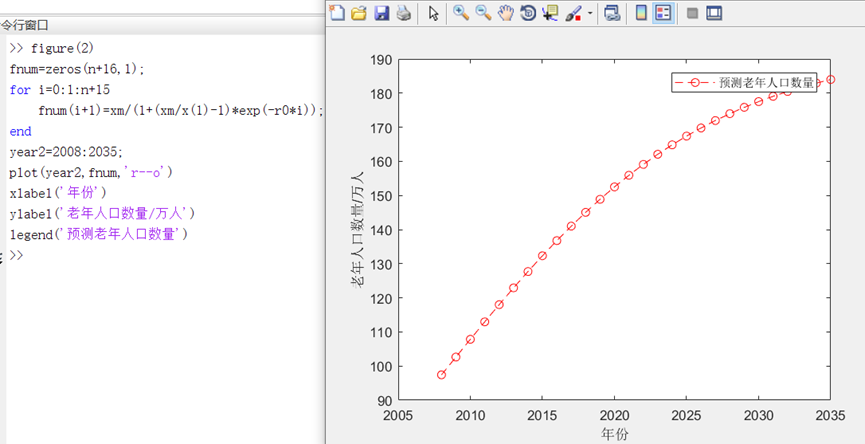
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/笔触狂放9/article/detail/629952
推荐阅读
相关标签


