高阶数据结构[3]图的遍历

图的两种遍历

前言

1.图的遍历

2.图的广度优先遍历

3.图的深度优先遍历

 4.总结

---

 

前言

书接上回，这篇文章将在图的存储结构上学习图的遍历方法。

图的遍历分为两种：1.BFS（Breadth First Search）宽度优先搜索

                                 2.DFS（Depth First Search)深度优先搜索

下面让我们一起来学习吧！ 注意，接下来的讲解基于图的邻接矩阵存储结构。

1.图的遍历

首先我们来了解什么叫做图的遍历，其实图的遍历也是将图的每一个结点进行访问。

 

上面这道经典的面试题就是有关图的遍历。

2.图的广度优先遍历

图的广度优先遍历，是指将同这个结点一层的结点优先遍历完全。 

这样一说大家是否想起来在二叉树遍历中的层序遍历呢！ 实际上，在广度优先遍历中确实能够使用层序遍历的思想进行算法的实现。

如下图，三个抽屉，我们在进行广度优先遍历时，三个抽屉的最外层为同一层，以此类推。

所以在进行广度优先遍历时，我们先走完三个抽屉的最外层再走中间最后走最下面的。

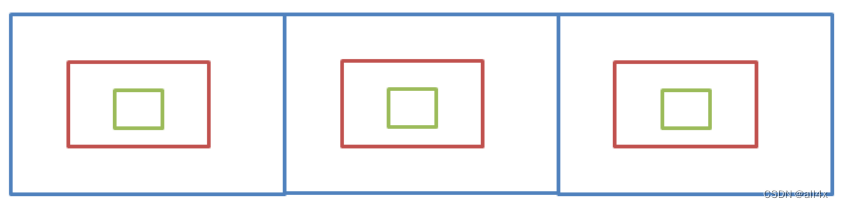
 我们用图来直观感受：

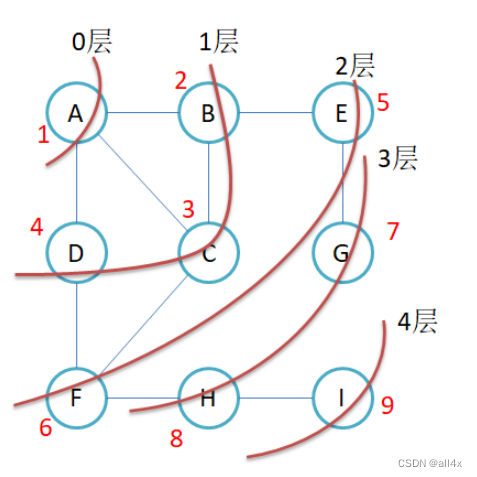
下面我们上代码,对照代码和上面的图我们可以看到，A先入队列，此后A出的时候带入与其相连的B,C,D。这时levelsize更新为3。B再出队列，B出的时候带入与B相连且未入队列的E。B出完，出C，同理带入F。以此类推就可以将上述图像进行广度优先遍历。

	void BFS(const V& src)
		{
			size_t scri = GetVertexIndex(src);
			//使用可变数组和队列进行标记
			queue<int>q;//记载已经遍历的点的下标，遍历过的点入队列.已经遍历的点从队列出来，与其相连的点入队列
			vector<bool>visited(_vertex.size(), false);//标记，来记载哪些顶点已经遍历，false为未遍历，遍历后该处改为true
			q.push(srci);//将遍历的点压入队列
			visited[srci] = true;
			int levelSize = 1;//BFS使用二叉树中层序遍历的思想
			size_t n = _vertexs.size();//_vertex存的是顶点值，即大小
			while (!q.empty())//队列不为空则要出顶点再带入相邻的顶点
			{
				//一层一层的出
				for (int j = 0; j < levelSize; j++)
				{
					int fornt = q.front();//记录队列顶的值
					q.pop();
					cout << fornt << ":" << _vertex[front] << " ";
					for (size_t i = 0; i < n; i++)//将同一层的点压入队列
					{
						if (_martix[front][i] != MAX_W)//说明二者相邻
						{
							if (visited[i] == false)//false则未访问过
							{
								q.push(i);//未访问的下标压入队列
								visited[i] = true;//该点访问过
							}
						}
					}
				}
				cout << endl;
              levelSize = q.size();
			}
			cout << endl;
		}

下面我们使用非层序的方法进行广度优先遍历的实现。这种方法实际上就是每一层基于矩阵的特性，n行n列。

void BFS(const V& scr)//宽搜的普通实现方法
		{
			size_t scri = GetVertexIndex(src);//取得顶点
			//标记队列和数组
			queue<int> q;
			vector<bool>visited(_vertex.size(), false)
				q.push(srci);
			visited[srci] = true;
			size_t n = _vertex.size();
			while (!q.empty())
			{
				int front = q.front();
				q.pop();
				for (int i = 0; i < n; i++)
				{
					if (_matrix[front][i] != MAX_W)
					{
						if (visited[i] == false)
						{
							q.push(i);
							visited[i] = true;
						}
					}
				}
			}
		}

3.图的深度优先遍历

 图的深度优先遍历即从一个点出发一直找到底再返回。还是经典的抽屉。

 

进行DFS时，是先将一个抽屉从最外面找到最里面才找下一个。我们看代码。

 

void _DFS(size_t i, vector<bool>visited)
		{
		
			visited[srci] = true;
			//找与srci相邻但未访问的点进行深度遍历
			for (size_t i = 0; i < n; i++)
			{
				if (_matrix[srci][i] != MAX_W && visited[i] == false)//两个点之间有边，且未访问
				{
					_DFS(i, visited);//递归实现
				}
			}
		}
 
		void DFS(const V& src)
		{
			size_t srci = GetVertexIndex(scr);
			vector<bool> visited(_vertexs.size(), false);
			_DFS(srci, visited);
		}

 4.总结

以上就是对图的遍历方式的讲解，这部分会比较困难，大家耐心学习。下一章节我们将讲解最小生成树的相关问题。