（dfs）（深度优先搜索算法）_dfs算法

目录

1.什么是dfs，以及算法的基础是什么？dfs:深度优先搜索算法，是一种用于遍历或搜索树或图的算法.沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。简单来说就是一条路走到黑，直到没路了，或者找到结果才返回。

2.可运用的问题：有组合问题，切割问题，子集问题，排列问题，棋盘问题这五种基本问题

3.如何去理解深度优先搜索的回溯算法

4.（回溯）样例

1.素数环一个环由n个圈组成，将自然数1-n放入圈内，使得任意相邻圈的两个数之和均为素数。第一个圈的元素均为1。下图为n=6时的一个例子：

2.题目：代码部队

3.题目：迷宫

4.题目：填涂颜色

5.题目：八皇后 Checker Challenge

6.题目：PERKET

7.题目：单词接龙

---

1.什么是dfs，以及算法的基础是什么？
dfs:深度优先搜索算法，是一种用于遍历或搜索树或图的算法.沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。简单来说就是一条路走到黑，直到没路了，或者找到结果才返回。

深度优先搜索算法的基础：递归与回溯

递归与回溯是相辅相成的，有递归就会有回溯，递归函数的下面部分就是回溯的过程以及回溯的逻辑（即递归是回溯的基础）

2.可运用的问题：有组合问题，切割问题，子集问题，排列问题，棋盘问题这五种基本问题

• 组合问题：N个数里面按一定规则找出k个数的集合
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 棋盘问题：N皇后，解数独等等

3.如何去理解深度优先搜索的回溯算法

回溯算法是一个很抽象的东西，但是所有的回溯算法都可以抽象成一个树状结构，可以将其抽象成一个n叉树问题。如果满足递归的条件，树枝可以无限增加，直到找到所需要数据为止，如果不满足，树枝则会折断。树的深度取决于要搜索问题的层数，树的宽度取决于每个节点处理集合的大小。为方便理解，我增加出以下模板：

void 函数名（参数）//回溯算法的参数一般比较多，要根据具体情况进行分析
{
    if(终止条件)
      {
         收集最后节点结果
         return  ;
      }
//单层搜索的逻辑:
    for(集合的元素）//遍历的是集合里的每一个元素，也可能是集合节点的子节点个数
      {
          处理节点
          递归函数
          回溯操作（撤销处理节点的操作）
      }
    return ；
}

4.（回溯）样例

1.素数环
一个环由n个圈组成，将自然数1-n放入圈内，使得任意相邻圈的两个数之和均为素数。第一个圈的元素均为1。下图为n=6时的一个例子：

                                        
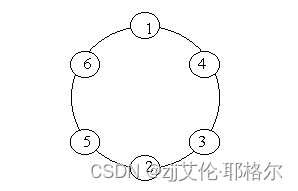
程序样例
输入为一个整数n

• 6
• 8

输出分别为

• 1 4 3 2 5 6
  1 6 5 2 3 4

• 1 2 3 8 5 6 7 4
  1 2 5 8 3 4 7 6
  1 4 7 6 5 8 3 2
  1 6 7 4 3 8 5 2

本题是可以直接套用上述模板来写的，可以仔细思考一。

话不多说，直接上代码，详细解释在代码注释中

#include<stdio.h>
#include<math.h>
int su(int m);        
void huan(int t);
int n;
int a[100]= {0};
int b[100]= {0};
int main() {
	scanf("%d",&n);
	a[0]=1;          //初始化变量
	b[0]=1;
	huan(1);          //从1开始遍列
	return 0;
 
}
 
void huan(int t) {
	int i;
	if(t==n&&su(a[n-1]+a[0])) {            //终止条件有两个，一个是首尾相接是否是素数，一个是圈内元素的个数，需要达到n（由用户输入）
		for(i=0; i<n; i++) {               //输出结果（但是每一次的输出都只是一个满足条件的“树枝”，不满足条件的会被筛掉）
			printf("%d ",a[i]);             //如果该if条件成立，则该“树枝”到头了 
		}
		printf("\n");
	} else {
		for(i=2; i<=n; i++) {
			if(b[i-1]==0) {              //是否被使用
				a[t]=i;                  //给数组a赋值
				b[i-1]=1;                //已经使用，在递归
				if(su(a[t]+a[t-1])) {     //回溯操作（这需要满足条件（为素数））
					huan(t+1);
				}
				b[i-1]=0;                 //递归完，在给第二次循环使用，确保数据不变
			}
		}
	}
}
 
int su(int m) {                  //该函数用于判断是否是素数，是huan函数的一个判断条件，对应模板中的终止条件
	int i;
	if(m<3) return 0;
	else {
		for(i=2; i<=sqrt(m); i++) {
			if(m%i==0) {
				return 0;
				break;
			}
		}
	}
	return 1;
}

2.题目：代码部队

.这一道作者本人好早之前写的题，方法一样。（但是链接一时半会没找到，撮合看吧）

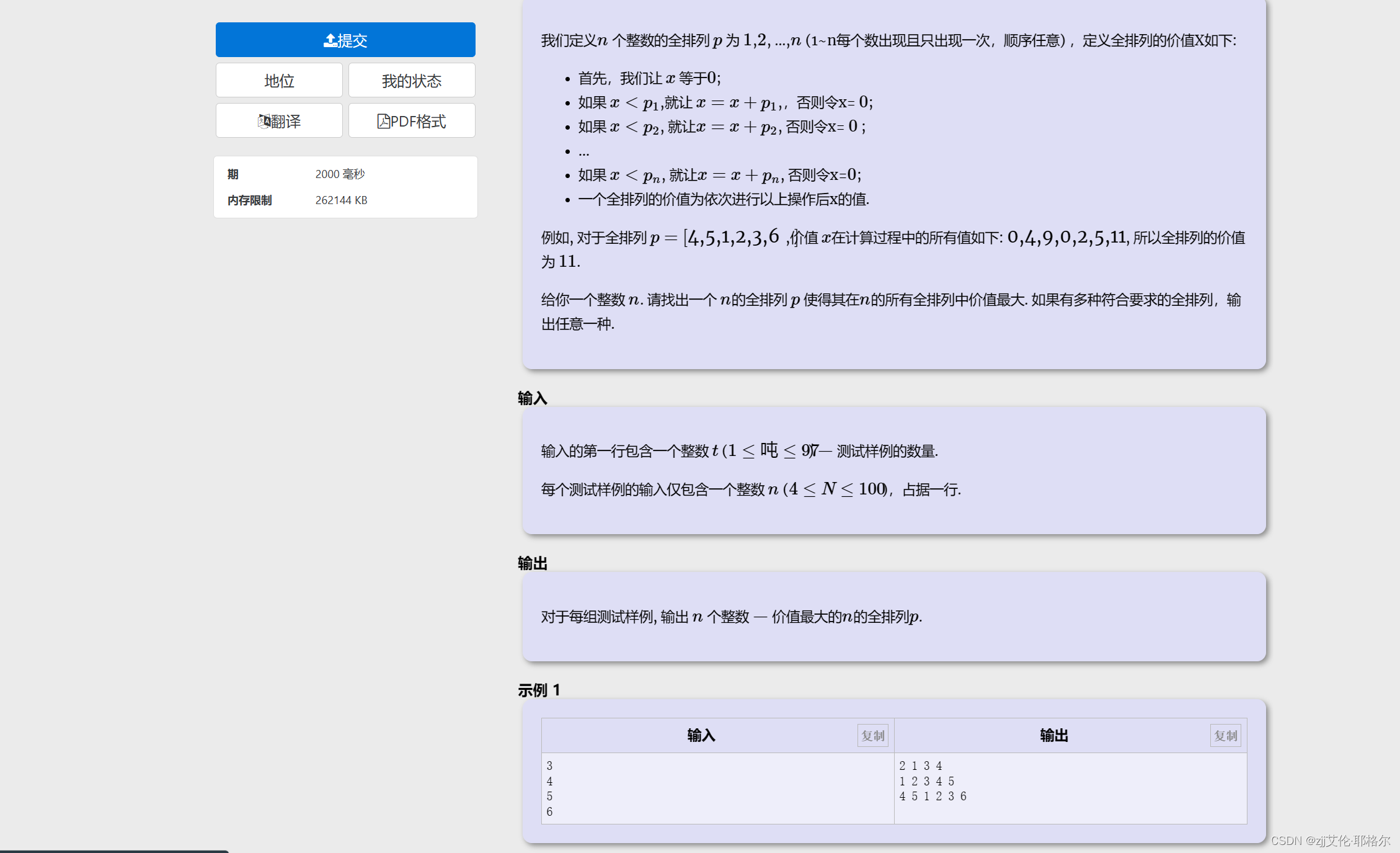
输入：

3
4
5
6

输出

2 1 3 4
1 2 3 4 5
4 5 1 2 3 6

方法一：找规律（因为只要输出全其中的一种，所以还是有规律的）

#include <stdio.h>
int main() {
	int m;
	scanf("%d",&m);
	while(m--) {
		int n,i;
		scanf("%d",&n);
		int a[101]= {0};      //定义数组
		a[n]=n,a[n-1]=n-1;;
		if(n==3) 
			a[1]=1,a[2]=2;	 
		else if(n%2==0) {
			for(i=1; i<=n-2; i++) {
				if(i%2==0) 
					a[i]=i-1;      //规律
				else
					a[i]=i+1;
				
			}
		}
 
		else  if(n%2!=0) {
			a[1]=1,a[2]=2,a[3]=3;
			for(i=4; i<=n-2; i++) {
				if(i%2==0) 
					a[i]=i+1;
				else
					a[i]=i-1;
			}
		}
 
		for(i=1; i<=n; i++) 
			printf("%d ",a[i]);
		printf("\n");
	}
	return 0;
}

方法二：当然就是我们现在讲的，you know

#include<stdio.h>
int su(int x,int p);        //回溯法
void huan(int t);
int n,x,y,z;                         //定义全局变量
int a[101]= {0};
int b[101]= {0};
int main() {
	int m;
	scanf("%d",&m);
	while(m--) {
		scanf("%d",&n);
		a[101]= {0},b[101]= {0};
		z=0;
		x=0;
		y=0;                   //因为要输入m次，要重新归0，否则只会输出一次结果
		a[n]=n;
		huan(1);                     //从1开始遍例
	}
	return 0;
}
void huan(int t) {
	int i;
	if(x==0&&y==n-1) {                         //输出条件，有n给数，并且x最后的值为n，并x在变化的过程中永远小于等于n
		for(i=1; i<=n; i++) {
			printf("%d ",a[i]);
		}
		printf("\n");
		z=1;                                  //防止继续输出结果而赋值，用于第40行的条件判定【if(z)break;】
	} else {
		for(i=1; i<n; i++) {                   //a[1]=i遍例
			int s=x;
			if(b[i]==0) {                //如果i没被使用
				a[t]=i;
				b[i]=1;                 //意味着i已经被使用过了
				y++;
				x=su(x,i);     //x的值变化
				if(x<n) {
					huan(t+1);
				}
				b[i]=0;              //保持原有值不变
				x=s;
				y--;
			}
				if(z)break;              //题目中说只输出一个n个数的答案即可，所以加终止条件
		}
 
	}
}
 
int su(int x,int p) {               //判断x的值的函数
	if(x<p)
		return x+p;
	else
		return 0;
}

3.题目：迷宫

题目链接：https://www.luogu.com.cn/problem/P1605​

输入：

2 2 1
1 1 2 2
1 2

输出:

1

这是洛谷上的一道dfs的入门题，我们通过这题来了解一下dfs

话不多说，直接上代码，当然，也不止我这一种方法，可能也有更好的

#include<stdio.h>
int a[11][11],l,r;
int dx[4]= {0,0,1,-1};
int dy[4]= {-1,1,0,0};                 //上加下减，左减右加
int n,m,t,sum=0,q,p;
void fun(int x,int y) {
	if(x==q&&y==p) {
		sum++;                              //终止条件，可以套用模板，但是sum得设置为全局变量
	} else {
		for(int i=0; i<=3; i++) {                         
			if(a[x+dx[i]][y+dy[i]]==0&&y+dy[i]>0&&x+dx[i]>0) {
				a[x][y]=1;                              //代表（x,y)已经走过了
			//	printf("  %d %d\n",q,p);                 //验证数据是否正确
				fun(x+dx[i],y+dy[i]);             //回溯，递归
				a[x][y]=0;                      //保证循环中数据不变
			}
		}
	}
 
}
 
int main() {
	int x,y;
	scanf("%d %d %d",&n,&m,&t);
	scanf("%d %d %d %d",&x,&y,&q,&p);
 
	for(int i=1; i<=t; i++) {
		scanf("%d %d",&l,&r);
		a[l][r]=1;                   //这里是障碍点，可以理解为不能走，可以设置为已经走过的，赋值为1
	}
 
	for(int i=1; i<=n; i++)   //墙壁   因为定义的数组大小是11*11的，如果不设置墙壁，就无法得到题目中说的n*m的矩形，所以要设置墙壁规定大小
		a[i][m+1]=1;
	for(int j=1; j<=m; j++)
		a[n+1][j]=1;
 
	fun(x,y);
	printf("%d",sum);
 
	return 0;
}

可以看到这个基础题的代码和上述模版十分相似，但是后续的难题就不能完全依靠模板了，那个只是起到一个辅助的思路，主要还是需要自己思考。

4.题目：填涂颜色

题目链接：https://www.luogu.com.cn/problem/P1162

输入：

6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1

输出：

0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1

没有充分利用dfs的模板，但是需要用到dfs的思路：

上代码：

#include <stdio.h>
int n,map[35][35],vis[35][35]; //大小n*n，图，是否访问过（0/1标记）
int dx[4]= {0,0,1,-1};
int dy[4]= {-1,1,0,0};
void dfs(int i,int j) {
	if(map[i][j] || vis[i][j] || i<1 ||i>n || j<1 || j>n)return;  //遇到由1组成墙壁会返回，遇到边界也会返回
	vis[i][j]=1;
	for(int z=0; z<=3; z++)                                       //四个方向递归
		dfs(i+dx[z],j+dy[z]);
}
int main() {
	scanf("%d",&n);
	for(int i=1; i<=n; i++)  //贪心，从边缘DFS一定能把所有外面的0都访问过
		for(int j=1; j<=n; j++)
			scanf("%d",&map[i][j]);
 
	for(int i=1; i<=n; i++) {         //确保无漏网之鱼
		dfs(1,i);
		dfs(n,i);                    //列（最左边和最右边）
		dfs(i,1);                    //行（最上边和最下边）
		dfs(i,n);
	}
 
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=n; j++)
			if(map[i][j])
				printf("%d ",1);
			else printf("%d ",vis[i][j]?0:2);      //运算符（更快）
		if(i!=n)
			printf("\n");
	}
	return 0;
}

5.题目：八皇后 Checker Challenge

想必前面的题都小菜一碟，解决起来都游刃有余，本也一样，不要被他外表迷惑，万变不离其宗

题目链接：https://www.luogu.com.cn/problem/P1219

输入：

6

输出：

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

代码如下：

#include<stdio.h>
#include<math.h>
int sum=0,n;
int a[50],b[50];
int fun(int x,int y) {
	for(int i=1; i<x; i++) {            //判断是否位于对角线上，是则返回0，不是返回1(这个本人是用斜率来判断的)
		int sj=abs(y-a[i]),sg=x-i;
		if(sj==sg)
			return 0;
	}
	return 1;
}
void fds(int m) {
	if(m>n) {
		if(sum<3) {                  //题目说只要输出前面三种即可
			for(int i=1; i<m; i++)
				printf("%d ",a[i]);
			printf("\n");
		}
		sum++;               //总解数
	} else {
		for(int i=1; i<=n; i++) {   //熟悉的模板
			a[m]=i;
			if(b[i]==0) {
				b[i]=1;             //已经被使用（在下一个递归中，他已经被使用的）
				if(fun(m,i))
					fds(m+1);
				b[i]=0;            //循环中数据不变，重新变为为被使用（在该循环过程中，他可以继续被使用）
			}
 
		}
	}
}
int main() {
	scanf("%d",&n);
	fds(1);
	printf("%d",sum);
	return 0;
}

6.题目：PERKET

既然你已经能够熟练掌握，那么下面这道题目也能轻松应对吧，这是一道让你更加自信的题目

题目链接：https://www.luogu.com.cn/problem/P2036

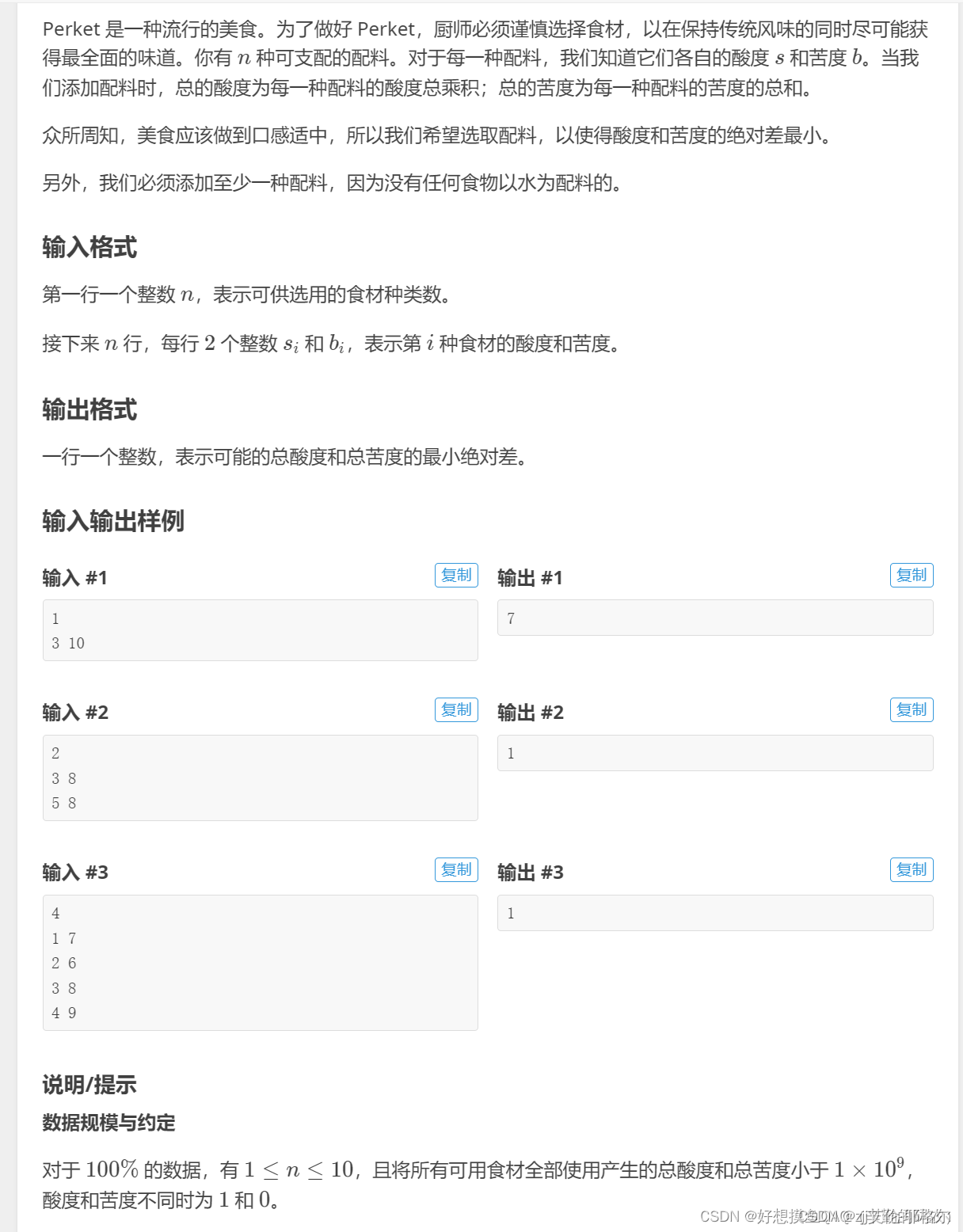
输入：

1
3 10

2
3 8
5 8

4
1 7
2 6
3 8
4 9

输出：

7

1

1

就不多解释了

#include<stdio.h>
#include<math.h>
struct ab {
	int a,b;
} sum[11];
int min,n,s,t=1,k=0,num[11];
void fds(int m) {
	for(int i=m; i<=n; i++) {
	
			t*=sum[i].a,k+=sum[i].b;
		if(min>abs(t-k))
			min=abs(t-k);
//	printf("%d %d\n",t,k);
		fds(i+1);
		t/=sum[i].a,k-=sum[i].b ;
		
	}
}
int main() {
	int i;
	scanf("%d",&n);
	for(i=1; i<=n; i++)
		scanf("%d %d",&sum[i].a,&sum[i].b);
	min=abs(sum[1].a-sum[1].b );
	fds(1);
	printf("%d",min);
	return 0;
}

7.题目：单词接龙

链接：单词接龙

我个人觉得还是挺有难度的，有兴趣的可以尝试。因为难一点，可能不容易理解，我会写一下我的思路，更加方便你们理解。

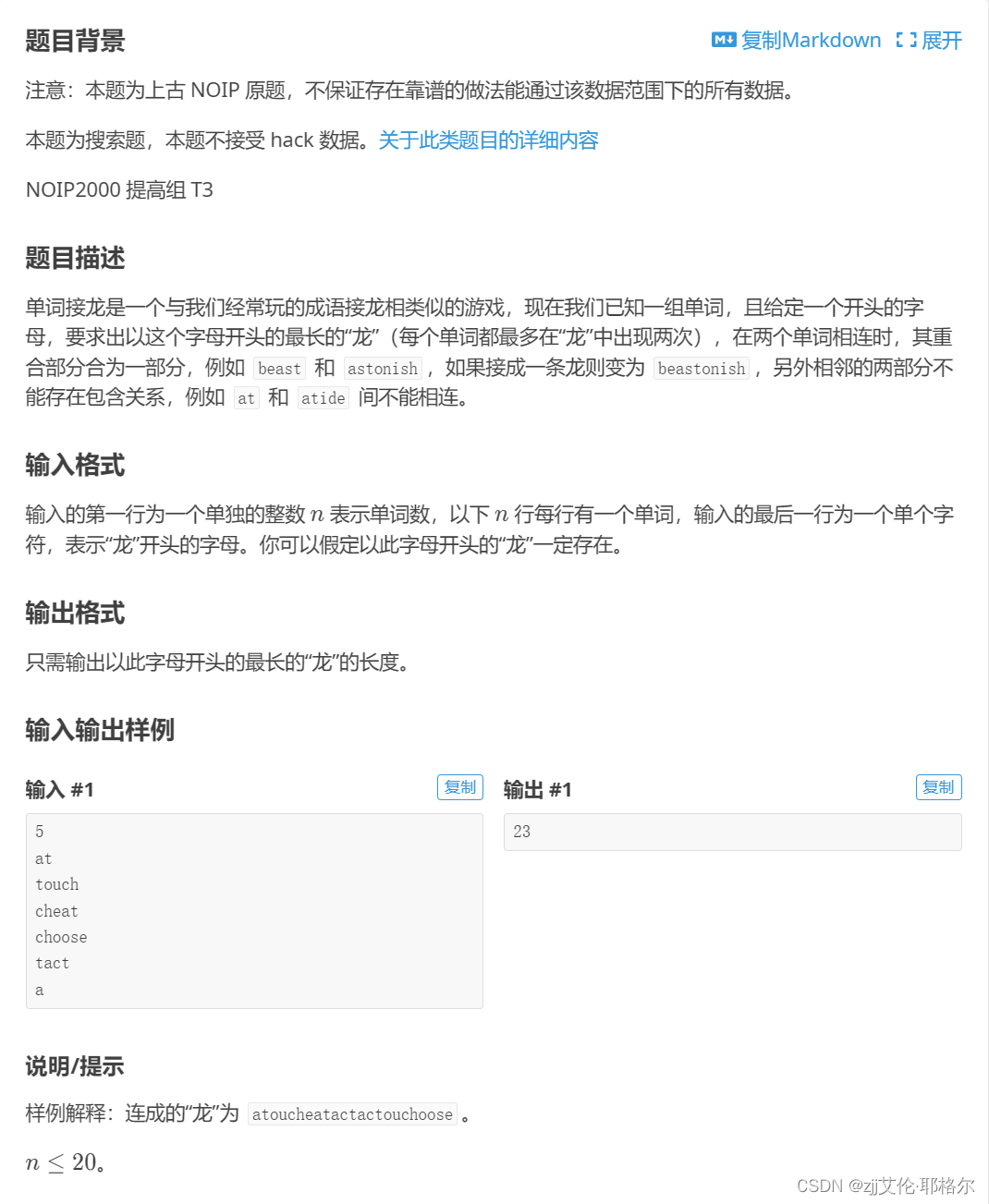
输入：

5
at
touch
cheat
choose
tact
a

输出：

23

思路：首先，四个关键点

1.两个单词合并时，合并部分取的是最小重叠部分

2.相邻的两部分不能存在包含关系就是说如果存在包含关系，就不能标记为使用过。

3.每个单词最多出现两次

4.输入的最后一行为一个单个字符，表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在。

我建议直接从第四行入手，先找到头，在找尾巴，因为这里就头和尾两部分，尾巴就需要考虑连接问题，所有我用mt函数，标记哪些单词可以首尾相接，y是尾巴，x是尾巴前面的一个单词，如果函数返回值是0，说明没有重和部分，如果是x的长度或者y的长度，则说明两者之间含有包含关系，也不行，还要注意单词使用次数，不能超过2次，然后在使用我们熟知的dfs即可，下面请看代码。

上代码：

#include<bits/stdc++.h>           //基本上所有题目都是可以分割成一部分一部分来写的
using namespace std;
int n;
char tr[30][100];                 //存储字符串
int ycl[30][30];                   //两个字母的最小重叠部分
int vis[30];                      //判断单词使用次数，超过2就不在使用
int mt(int x, int y) {           //判断能不能链接，能的话返回x单词后连接一个y单词的最小重叠部分,这里x表示尾巴，y表示要连接的单词
	bool sb=true;                 // 1  是不是显得很高级，当然，也可以用 int 然后1 0表示正确 错误
	int ky=0;
	for(int i=strlen(tr[x])-1; i>=0; i--) { //从x单词尾部向前看看最小重叠部分是从哪里开始的，以为因为是倒着来，所以保证是最小的
		for(int j=i; j<strlen(tr[x]); j++) {
			if(tr[x][j]!=tr[y][ky++]) {
				sb=false;            // 0
				break;
			}
		}
		if(sb)                     //如果说当前以k为开头的前一个单词后缀 ,是后面单词的前缀，就马上返回重叠部分。（strlen(x)-i是找出来的规律）
			return strlen(tr[x])-i; //直接结束函数
		ky=0;
		sb=true;                   //不行就继续,然后变量初始化
	}
	return 0;
}
 
char ch;                           //记录开头字母
int sum=-1;                        //答案（英文忘了怎么打了）
int num=0;                          //每次搜到的当前最长串
void dfs(int p) {                  //p为尾部单词编号(p的后缀就是“龙”的后缀，因为p已经连接到”龙“后面了)
	bool sb=false;                 // 0
	for(int j=1; j<=n; j++) {
		if(vis[j]>=2) continue;    //使用了两次就跳过
		if(ycl[p][j]==0) continue;  //两单词之间没有重合部分就跳过
		if(ycl[p][j]==strlen(tr[p]) || ycl[p][j]==strlen(tr[j])) continue;//两者存在包含关系就跳过
		num+=strlen(tr[j])-ycl[p][j];      //两单词合并再减去最小重合部分
		vis[j]++;                     //使用次数加1
		sb=true;                      //标记一下当前已经成功匹配到一个可以连接的部分
		dfs(j);                       //接上去
		num-=strlen(tr[j])-ycl[p][j];   //回溯，就要再减回去那一部分长度
		vis[j]--;                    //模板了，初始化变量
	}
	if(sb==false) {                   //jx==false说明不能再找到任何一个单词可以相连了
		sum=max(sum,num);              //更新ans,只要最大值
	}
	return;
}
 
int main() {  //注意，这个才是主函数
	cin>>n;
	for(int i=1; i<=n; i++)
		cin>>tr[i];
	cin>>ch;
	for(int i=1; i<=n; i++)
		for(int j=1; j<=n; j++)
			ycl[i][j]=mt(i,j);  //提前处理，这里哪些单词可以接在哪些单词的后面
 
	for(int i=1; i<=n; i++) { //从头到尾看一下有没有以指定开头字母为开头的单词
		if(tr[i][0]==ch) {  //如果有，就以当前单词为基准进行搜索。
			vis[i]++;       //使用次数加1
			num=strlen(tr[i]);  //更新当前串长度
			dfs(i);         //接上
			vis[i]=0;       //变量初始化
		}
	}
	printf("%d",sum);
	return 0;
}

小结：平凡不一定平庸