为实习准备的数据结构（11）-- 图论算法 集锦(1)_前端数据结构图论

这许许多多地铁站所组成的交通网络，也可以认为是数据结构当中的图。

图，是一种比树更为复杂的数据结构。树的节点之间是一对多的关系，并且存在父与子的层级划分；而图的顶点（注意，这里不叫节点）之间是多对多的关系，并且所有顶点都是平等的，无所谓谁是父谁是子。

---

图的相关定义

---

定义一：有向图、无向图、权重、活用图

图是由顶点的有穷非空集合和顶点之间边的集合组成， 通常表示为: G（V，E）， 其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

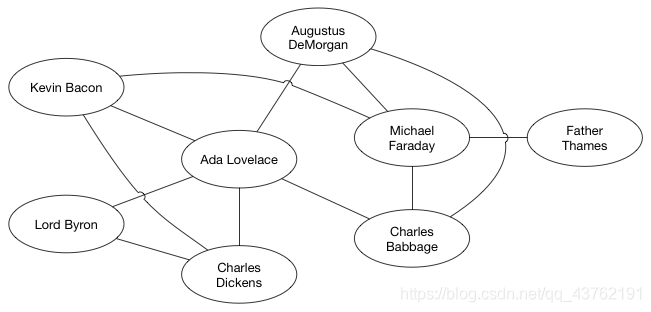
这种叫做无向图，里面的边叫做无向边。

图有各种形状和大小。边可以有权重（weight），即每一条边会被分配一个正数或者负数值。考虑一个代表航线的图。各个城市就是顶点，航线就是边。那么边的权重可以是飞行时间，或者机票价格。

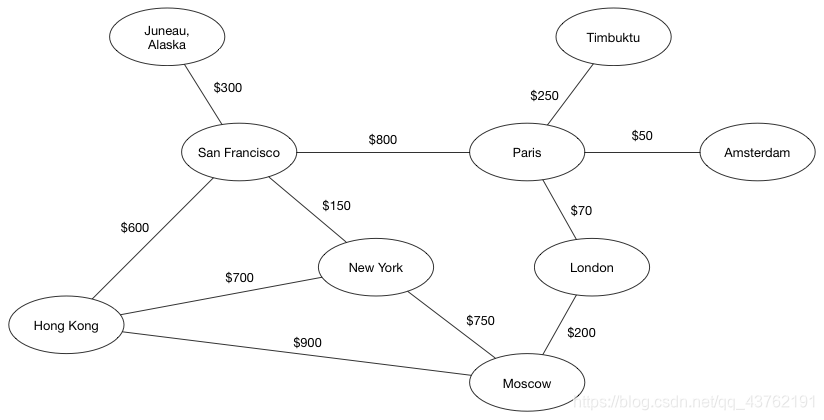
边可以是有方向的。在上面提到的例子中，边是没有方向的。有方向的边意味着是单方面的关系。

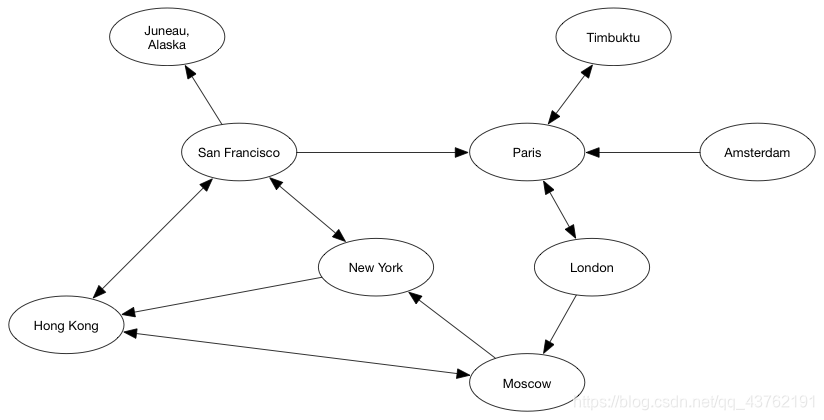
事实证明图是一种有用的数据结构。

如果你有一个编程问题可以通过顶点和边表示出来，那么你就可以将你的问题用图画出来，然后使用著名的图算法（比如广度优先搜索 或者 深度优先搜索）来找到解决方案。

离散数学中有不少这方面的栗子。

假设你有一系列任务需要完成，但是有的任务必须等待其他任务完成后才可以开始。你可以通过非循环有向图来建立模型：

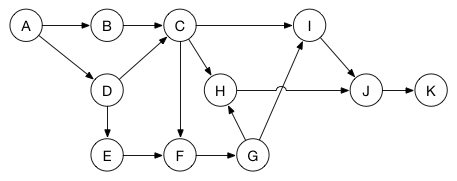
每一个顶点代表一个任务。两个任务之间的边表示目的任务必须等到源任务完成后才可以开始。比如，在任务B和任务D都完成之前，任务C不可以开始。在任务A完成之前，任务A和D都不能开始。

现在这个问题就通过图描述清楚了，你可以使用深度优先搜索算法来执行执行拓扑排序。这样就可以将所有的任务排入最优的执行顺序，保证等待任务完成的时间最小化。（这里可能的顺序之一是：A, B, D, E, C, F, G, H, I, J, K）

---

定义二：完全图、连通图、连通分量、生成树

在图中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图。目前讨论的都是简单图。在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。含有n个顶点的无向完全图有n*(n-1)/2条边。在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。含有n个顶点的有向完全图有n* (n-1) 条边。

在无向图G中，如果从顶点v到顶点v’有路径，则称v和v’是连通的。 如果对于图中任意两个顶点vi、vj ∈E， vi，和vj都是连通的，则称G是连通图。

无向图中的极大连通子图称为连通分量。注意连通分量的概念，它强调:

要是子图；

子图要是连通的；

连通子图含有极大顶点数；

具有极大顶点数的连通子图包含依附于这些顶点的所有边。

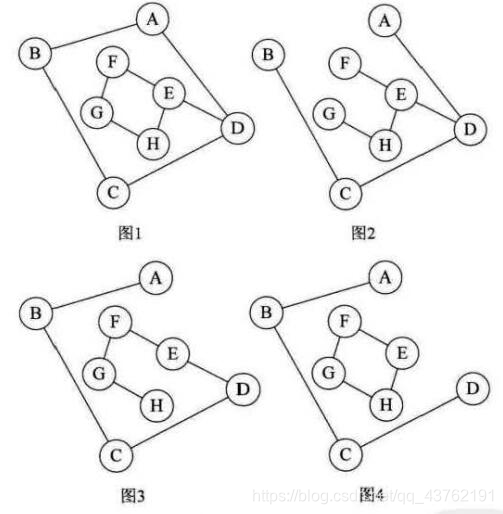
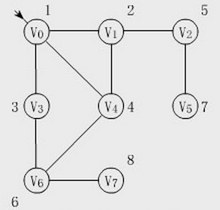
所谓的一个连通图的生成树是一个极小的连通子图， 它含有图中全部的n 个顶点，但只有足以构成一棵树的n-1条边。比如下图的图1是一普通图，但显然它不是生成树，当去掉两条构成环的边后，比如图2 或图3，就满足n个顶点n-1条边且连通的定义了， 它们都是一棵生成树。从这里也可知道，如果一个图有n 个顶点和小子n-1条边，则是非连通图，如果多于n-1 边条，必定构成一个环， 因为这条边使得它依附的那两个顶点之间有了第二条路径。比如图2 和图3，随便加哪两顶点的边都将构成环。 不过有n-1条边并不一定是生成树，比如图4。

定义三：邻接表、邻接矩阵

理论上，图就是一堆顶点和边对象而已，但是怎么在代码中来描述呢？

有两种主要的方法：邻接列表和邻接矩阵。

在邻接列表实现中，每一个顶点会存储一个从它这里开始的边的列表。比如，如果顶点A 有一条边到B、C和D，那么A的列表中会有3条边

在邻接矩阵实现中，由行和列都表示顶点，由两个顶点所决定的矩阵对应元素表示这里两个顶点是否相连、如果相连这个值表示的是相连边的权重。例如，如果从顶点A到顶点B有一条权重为 5.6 的边，那么矩阵中第A行第B列的位置的元素值应该是5.6：

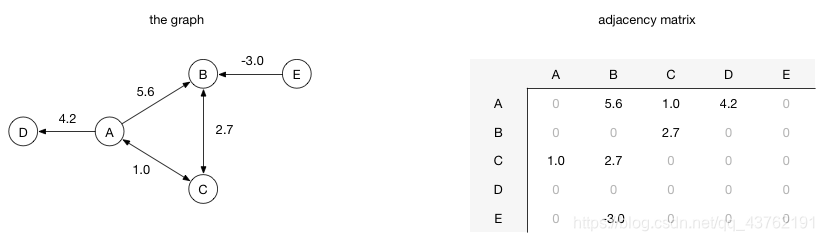
邻接列表只描述了指向外部的边。A 有一条边到B，但是B没有边到A，所以 A没有出现在B的邻接列表中。查找两个顶点之间的边或者权重会比较费时。

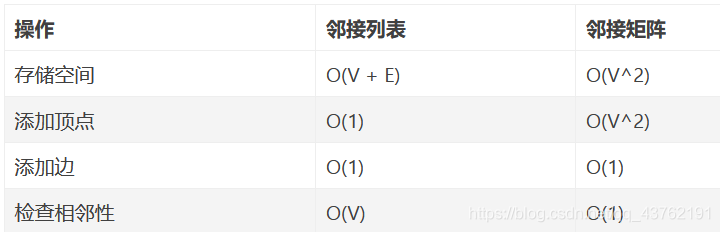
所以使用哪一个呢？大多数时候，选择邻接列表是正确的。下面是两种实现方法更详细的比较：

---

定义四：DFS、BFS

(1) 深度优先遍历（DFS）

a. 访问顶点v

b. 依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问

c. 若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止

(2) 广度优先遍历（BFS）

a. 从图中某个顶点v出发，访问v

b. 依次访问v的各个未被访问过的邻接点

c. 分别从这些邻接点出发依次访问他们的邻接点

d. 重复步骤c，直至所有已被访问的顶点的邻接点都被访问到

---

定义五：Prim 算法、Kruskal 算法、Dijkstra 算法

Prim 算法

a. 以某一个点开始，寻找当前该点可以访问的所有的边

b. 在已经寻找的边中发现最小边，这个边必须有一个点还没有访问过，将还没有访问的点加入集合，记录添加的边

c. 寻找当前集合可以访问的所有边，重复 b 的过程，直到没有新的点可以加入

Kruskal 算法

a. 设一个有n个顶点的连通网络为 G（V,E），最初先构造一个只有 n 个顶点，没有边的非连通图 T，图中每个顶点自成一个连通分量

b. 当在E中选择一条具有最小权值的边时，若该边的两个顶点落在不同的连通分量上，则将此边加入到 T 中；否则重新选择一条权值最小的边

c. 如此重复下去，直到所有顶点在同一个连通分量上为止

Dijkstra 算法

a. 遍历与结点1相连的所有结点，找到距离最近的一个，把这个结点标记为访问过，并更新最短路径

b. 遍历最短路径包含的点相连的节点，找到距离最近的加入最短路径，并且标记为访问过

c. 重复 b 步骤

总结：先遍历一遍还没有在最短路径中的点，选出一个距离最近的点，把它加入到最短路径中并更新，直到所有的点都加入到最短路径中。

---

存储结构

---

邻接表

得拿俩栗子来看，不然看着晕晕的。

如图是一个无向图的连接表结构，有向图则类似。

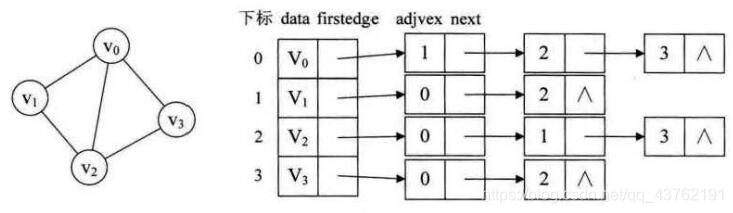
对于带权值的网图，可以在边表结点定义中再增加一个weight 的数据域，存储权值信息即可，如下图所示。

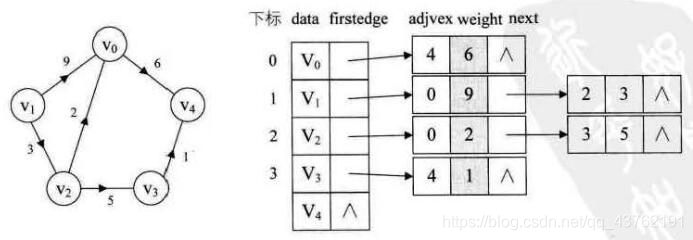
邻接表结点定义：

typedef char VertexType; /* 顶点类型应由用户定义 */

typedef int EdgeType; /* 边上的权值类型应由用户定义 */

typedef struct EdgeNode /* 边表结点 */

{

int adjvex; /* 邻接点域,存储该顶点对应的下标 */

EdgeType info; /* 用于存储权值,对于非网图可以不需要 */

struct EdgeNode next; / 链域,指向下一个邻接点 */

}EdgeNode;

typedef struct VertexNode /* 顶点表结点 */

{

VertexType data; /* 顶点域,存储顶点信息 */

EdgeNode firstedge;/ 边表头指针 */

}VertexNode, AdjList[MAXVEX];

typedef struct

{

AdjList adjList;

int numNodes,numEdges; /* 图中当前顶点数和边数 */

}GraphAdjList;

无向图的邻接表创建代码如下：

• 建立图的邻接表结构 */

void CreateALGraph(GraphAdjList *G)

{

int i,j,k;

EdgeNode *e;

printf(“输入顶点数和边数:\n”);

scanf(“%d,%d”,&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */

for(i = 0;i < G->numNodes;i++) /* 读入顶点信息,建立顶点表 */

{

scanf(&G->adjList[i].data); /* 输入顶点信息 */

G->adjList[i].firstedge=NULL; /* 将边表置为空表 */

}

for(k = 0;k < G->numEdges;k++)/* 建立边表 */

{

printf(“输入边(vi,vj)上的顶点序号:\n”);

scanf(“%d,%d”,&i,&j); /* 输入边(vi,vj)上的顶点序号 */

e=(EdgeNode )malloc(sizeof(EdgeNode)); / 向内存申请空间,生成边表结点 */

e->adjvex=j; /* 邻接序号为j */

e->next=G->adjList[i].firstedge; /* 将e的指针指向当前顶点上指向的结点 */

G->adjList[i].firstedge=e; /* 将当前顶点的指针指向e */

e=(EdgeNode )malloc(sizeof(EdgeNode)); / 向内存申请空间,生成边表结点 */

e->adjvex=i; /* 邻接序号为i */

e->next=G->adjList[j].firstedge; /* 将e的指针指向当前顶点上指向的结点 */

G->adjList[j].firstedge=e; /* 将当前顶点的指针指向e */

}

}

---

邻接矩阵

如下无向图，

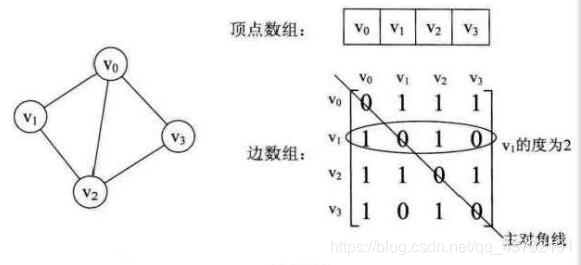
如下有向图，

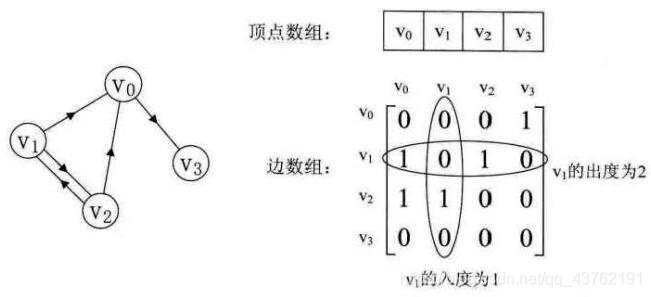
如下网图：

---

邻接矩阵结构：

#define OK 1

#define ERROR 0

#define TRUE 1

#define FALSE 0

#define MAXVEX 100 /* 最大顶点数，应由用户定义 */

#define INFINITY 65535

typedef int Status; /* Status是函数的类型,其值是函数结果状态代码，如OK等 */

typedef char VertexType; /* 顶点类型应由用户定义 */

typedef int EdgeType; /* 边上的权值类型应由用户定义 */

typedef struct

{

VertexType vexs[MAXVEX]; /* 顶点表 */

EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵，可看作边表 */

int numNodes, numEdges; /* 图中当前的顶点数和边数 */

}MGraph;

有了这个结构定义，我们构造一个图，其实就是给顶点表和边表输入数据的过程。我们来看看无向网图的创建代码。

/* 建立无向网图的邻接矩阵表示 */

void CreateMGraph(MGraph *G)

{

int i,j,k,w;

printf(“输入顶点数和边数:\n”);

scanf(“%d,%d”,&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */

for(i = 0;i numNodes;i++) /* 读入顶点信息,建立顶点表 */

scanf(&G->vexs[i]);

for(i = 0;i numNodes;i++)

for(j = 0;j numNodes;j++)

G->arc[i][j]=INFINITY; /* 邻接矩阵初始化 */

for(k = 0;k numEdges;k++) /* 读入numEdges条边，建立邻接矩阵 */

{

printf(“输入边(vi,vj)上的下标i，下标j和权w:\n”);

scanf(“%d,%d,%d”,&i,&j,&w); /* 输入边(vi,vj)上的权w */

G->arc[i][j]=w;

G->arc[j][i]= G->arc[i][j]; /* 因为是无向图，矩阵对称 */

}

}

从代码中也可以得到，n 个顶点和e 条边的无向网图的创建，时间复杂度O(n^2)。

---

遍历

---

DFS：深度优先

如果使用邻接矩阵，代码如下：

Boolean visited[MAXVEX]; /* 访问标志的数组 */

/* 邻接矩阵的深度优先递归算法 */

void DFS(MGraph G, int i)

{

int j;

visited[i] = TRUE;

printf("%c ", G.vexs[i]);/* 打印顶点，也可以其它操作 */

for(j = 0; j < G.numVertexes; j++)

if(G.arc[i][j] == 1 && !visited[j])

DFS(G, j);/* 对为访问的邻接顶点递归调用 */

}

/* 邻接矩阵的深度遍历操作 */

void DFSTraverse(MGraph G)

{

int i;

for(i = 0; i < G.numVertexes; i++)

visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */

for(i = 0; i < G.numVertexes; i++)

if(!visited[i]) /* 对未访问过的顶点调用DFS，若是连通图，只会执行一次 */

DFS(G, i);

}

如果使用邻接表结构，代码如下：

Boolean visited[MAXSIZE]; /* 访问标志的数组 */

/* 邻接表的深度优先递归算法 */

void DFS(GraphAdjList GL, int i)

{

EdgeNode *p;

visited[i] = TRUE;

printf("%c ",GL->adjList[i].data);/* 打印顶点,也可以其它操作 */

p = GL->adjList[i].firstedge;

while§

{

if(!visited[p->adjvex])

DFS(GL, p->adjvex);/* 对为访问的邻接顶点递归调用 */

p = p->next;

}

}

/* 邻接表的深度遍历操作 */

void DFSTraverse(GraphAdjList GL)

{

int i;

for(i = 0; i < GL->numVertexes; i++)

visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */

for(i = 0; i < GL->numVertexes; i++)

if(!visited[i]) /* 对未访问过的顶点调用DFS,若是连通图,只会执行一次 */

DFS(GL, i);

}

---

BFS：广度优先

如果说图的深度优先遍历类似树的前序遍历， 那么图的广度优先遍历就类似于树的层序遍历了。

以下是邻接矩阵结构的广度优先遍历算法：

/* 邻接矩阵的广度遍历算法 */

void BFSTraverse(MGraph G)

{

int i, j;

Queue Q;

for(i = 0; i < G.numVertexes; i++)

visited[i] = FALSE;

InitQueue(&Q); /* 初始化一辅助用的队列 */

for(i = 0; i < G.numVertexes; i++) /* 对每一个顶点做循环 */

{

if (!visited[i]) /* 若是未访问过就处理 */

{

visited[i]=TRUE; /* 设置当前顶点访问过 */

printf("%c ", G.vexs[i]);/* 打印顶点，也可以其它操作 */

EnQueue(&Q,i); /* 将此顶点入队列 */

while(!QueueEmpty(Q)) /* 若当前队列不为空 */

{

DeQueue(&Q,&i); /* 将队对元素出队列，赋值给i */

for(j=0;j<G.numVertexes;j++)

{

/* 判断其它顶点若与当前顶点存在边且未访问过 */

if(G.arc[i][j] == 1 && !visited[j])

{

visited[j]=TRUE; /* 将找到的此顶点标记为已访问 */

printf("%c ", G.vexs[j]); /* 打印顶点 */

EnQueue(&Q,j); /* 将找到的此顶点入队列 */

}

}

}

}

}

}

对于邻接表的广度优先遍历，代码与邻接矩阵差异不大，代码如下：

/* 邻接表的广度遍历算法 */

void BFSTraverse(GraphAdjList GL)

{

int i;

EdgeNode *p;

Queue Q;

for(i = 0; i < GL->numVertexes; i++)

visited[i] = FALSE;

InitQueue(&Q);

for(i = 0; i < GL->numVertexes; i++)

{

if (!visited[i])

{

visited[i]=TRUE;

printf("%c ",GL->adjList[i].data);/* 打印顶点,也可以其它操作 */

EnQueue(&Q,i);

while(!QueueEmpty(Q))

{

DeQueue(&Q,&i);

p = GL->adjList[i].firstedge; /* 找到当前顶点的边表链表头指针 */

while§

{

if(!visited[p->adjvex]) /* 若此顶点未被访问 */

{

visited[p->adjvex]=TRUE;

printf("%c ",GL->adjList[p->adjvex].data);

EnQueue(&Q,p->adjvex); /* 将此顶点入队列 */

}

p = p->next; /* 指针指向下一个邻接点 */

}

}

}

}

}

---

最小生成树

---

这俩算法倒是在运筹学里学过。

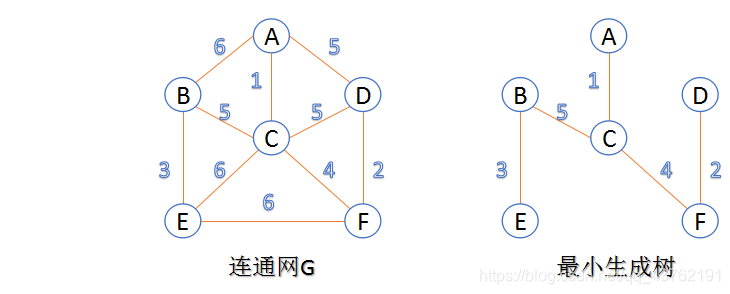
Prim算法

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

1、图的所有顶点集合为V；初始令集合u={s},v=V−u;

2、在两个集合u,v能够组成的边中，选择一条代价最小的边(u0,v0)，加入到最小生成树中，并把v0并入到集合u中。

3、重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

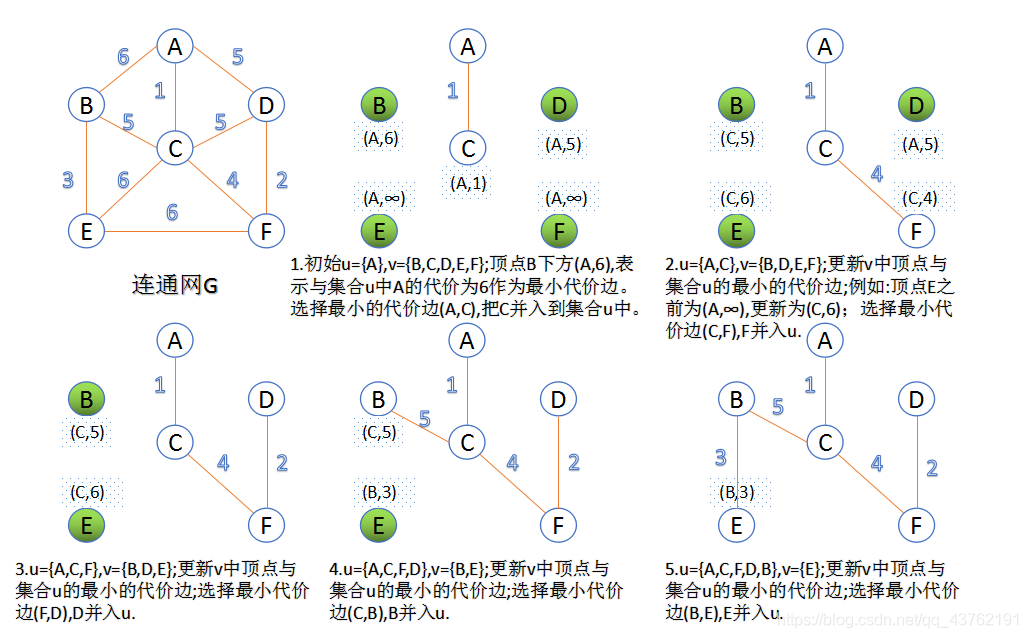
（先将图构造成一个邻接矩阵G）

/* Prim算法生成最小生成树 */

void MiniSpanTree_Prim(MGraph G)

{

int min, i, j, k;

int adjvex[MAXVEX]; /* 保存相关顶点下标 */

int lowcost[MAXVEX]; /* 保存相关顶点间边的权值 */

lowcost[0] = 0;/* 初始化第一个权值为0，即v0加入生成树 */

/* lowcost的值为0，在这里就是此下标的顶点已经加入生成树 */

adjvex[0] = 0; /* 初始化第一个顶点下标为0 */

for(i = 1; i < G.numVertexes; i++) /* 循环除下标为0外的全部顶点 */

{

lowcost[i] = G.arc[0][i]; /* 将v0顶点与之有边的权值存入数组 */

adjvex[i] = 0; /* 初始化都为v0的下标 */

}

for(i = 1; i < G.numVertexes; i++)

{

min = INFINITY; /* 初始化最小权值为∞， */

/* 通常设置为不可能的大数字如32767、65535等 */

j = 1;k = 0;

while(j < G.numVertexes) /* 循环全部顶点 */

{

if(lowcost[j]!=0 && lowcost[j] < min)/* 如果权值不为0且权值小于min */

{

min = lowcost[j]; /* 则让当前权值成为最小值 */

k = j; /* 将当前最小值的下标存入k */

}

j++;

}

printf(“(%d, %d)\n”, adjvex[k], k);/* 打印当前顶点边中权值最小的边 */

lowcost[k] = 0;/* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */

for(j = 1; j < G.numVertexes; j++) /* 循环所有顶点 */

{

if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j])

{/* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */

lowcost[j] = G.arc[k][j];/* 将较小的权值存入lowcost相应位置 */

adjvex[j] = k; /* 将下标为k的顶点存入adjvex */

}

}

}

}

---

Kruskal算法

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

1. 把图中的所有边按代价从小到大排序；

2. 把图中的n个顶点看成独立的n棵树组成的森林；

3. 按权值从小到大选择边，所选的边连接的两个顶点ui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。

4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

typedef struct

{

int begin;

int end;

int weight;

}Edge; /* 对边集数组Edge结构的定义 */

/* 生成最小生成树 */

void MiniSpanTree_Kruskal(MGraph G)

{

int i, j, n, m;

int k = 0;

int parent[MAXVEX];/* 定义一数组用来判断边与边是否形成环路 */

Edge edges[MAXEDGE];/* 定义边集数组,edge的结构为begin,end,weight,均为整型 */

/* 用来构建边集数组并排序********************* */

for ( i = 0; i < G.numVertexes-1; i++)

{

for (j = i + 1; j < G.numVertexes; j++)

{

if (G.arc[i][j]<INFINITY)

{

edges[k].begin = i;

edges[k].end = j;

edges[k].weight = G.arc[i][j];

k++;

}

}

}

sort(edges, &G);

/* ******************************************* */

for (i = 0; i < G.numVertexes; i++)

parent[i] = 0; /* 初始化数组值为0 */

printf(“打印最小生成树：\n”);

for (i = 0; i < G.numEdges; i++) /* 循环每一条边 */

{

n = Find(parent,edges[i].begin);

m = Find(parent,edges[i].end);

if (n != m) /* 假如n与m不等，说明此边没有与现有的生成树形成环路 */

{

parent[n] = m; /* 将此边的结尾顶点放入下标为起点的parent中。 */

/* 表示此顶点已经在生成树集合中 */

printf(“(%d, %d) %d\n”, edges[i].begin, edges[i].end, edges[i].weight);

}

}

}

克鲁斯卡尔算法主要是针对边来展开，边数少时效率会非常高，所以对于稀疏图有很大的优势； 而普里姆算法对于稠密图，即边数非常多的情况会更好一些。

---

最短路径

---

对于网图来说，最短路径，是指两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点。关于最短路径主要有两种算法，迪杰斯特拉(Dijkstra) 算法和弗洛伊德(Floyd) 算法。

这俩算法在运筹学中也学了。

Dijkstra 算法

文字解释枯燥无味，我选择看图：（求解节点“1”到其他所有节点的最短路径）

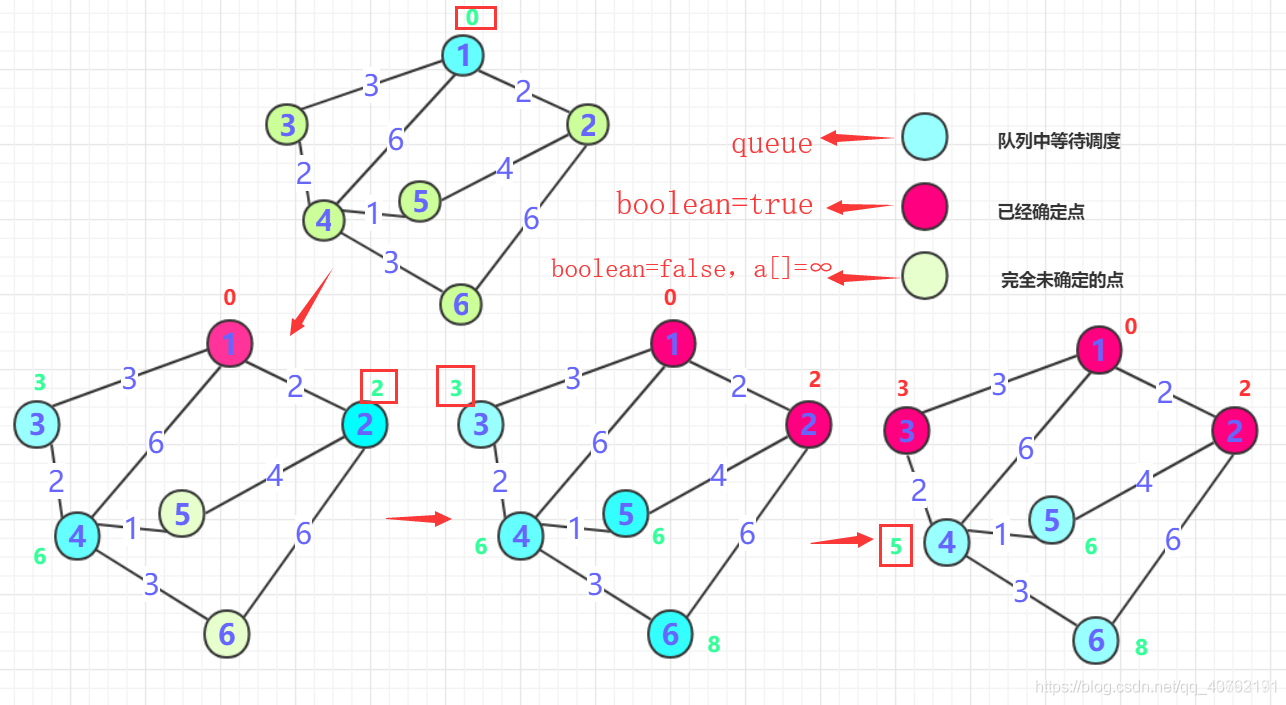
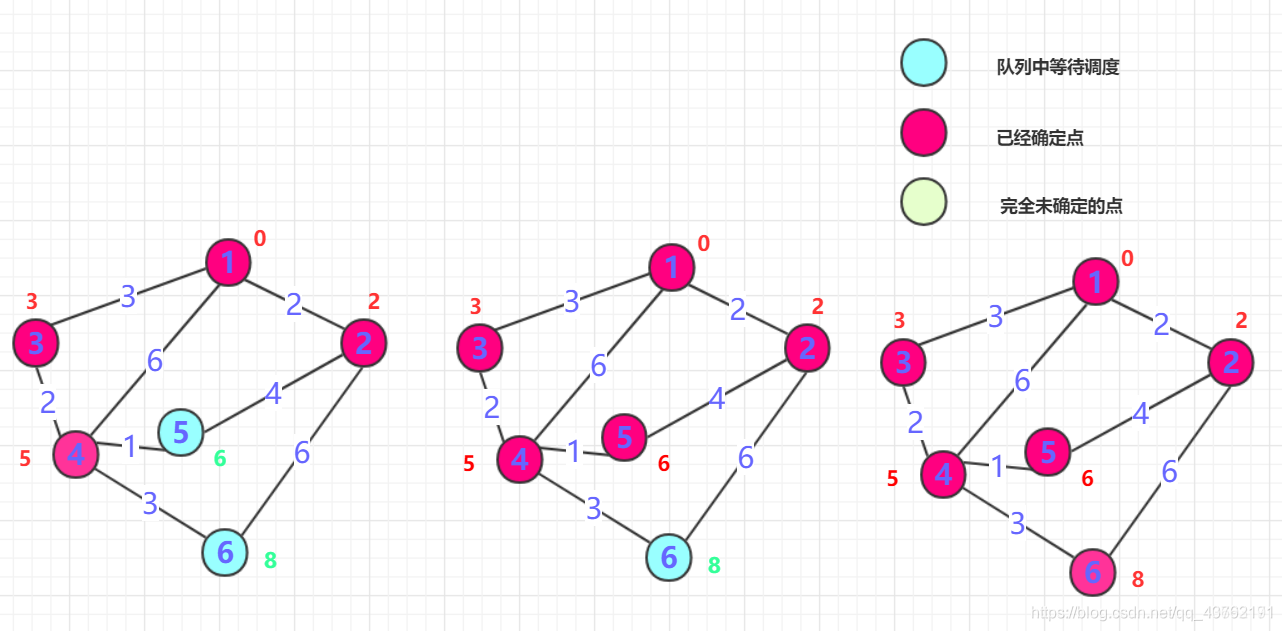
这是我能找到的最容易理解的图了，其他图文讲的讳莫如深，我不喜欢。

上面这两张理解完，再重新看一套，上面这两张是用来了解一下啥是迪杰斯特拉算法，接下来这套是用来写代码的：

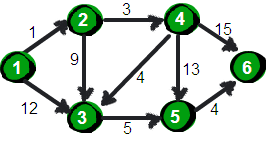
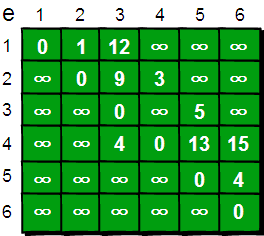
下面我们来模拟一下：

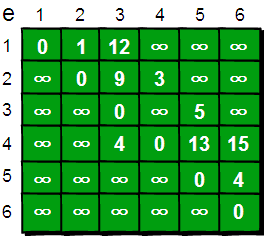
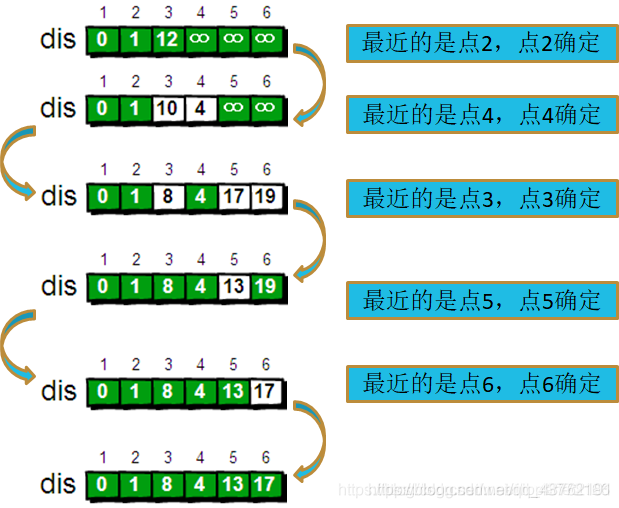
直接看这套的时候，会有点晕，不过有前面那套的铺垫，就好多了。

#include

#include

using namespace std;

const int INF = 0x3f3f3f3f, N = 205;

int ma[N][N];

int dis[N];

bool vis[N];

int n, m, st, ed;

void init()

{

// 初始化ma数组

for (int i = 0; i < n; i++)

for (int j = 0; j < n; j++)

ma[i][j] = (i == j ? 0 : INF);

}

void Dijk()

{

for (int i = 0; i < n - 1; i++){

int minv = INF, k; // k用来存储最小的且没被松弛过的城市

for (int j = 0; j < n; j++){

if (minv > dis[j] && !vis[j]){

minv = dis[j];

k = j;

}

自我介绍一下，小编13年上海交大毕业，曾经在小公司待过，也去过华为、OPPO等大厂，18年进入阿里一直到现在。

深知大多数Java工程师，想要提升技能，往往是自己摸索成长或者是报班学习，但对于培训机构动则几千的学费，着实压力不小。自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

因此收集整理了一份《2024年Java开发全套学习资料》，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友，同时减轻大家的负担。

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，基本涵盖了95%以上Java开发知识点，真正体系化！

由于文件比较大，这里只是将部分目录截图出来，每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频，并且会持续更新！

如果你觉得这些内容对你有帮助，可以扫码获取！！（备注Java获取）

Kafka实战笔记

关于这份笔记，为了不影响大家的阅读体验，我只能在文章中展示部分的章节内容和核心截图

• Kafka入门
• 为什么选择Kafka
• Karka的安装、管理和配置

• Kafka的集群
• 第一个Kafka程序
• 

afka的生产者

• Kafka的消费者
• 深入理解Kafka
• 可靠的数据传递

• Spring和Kalka的整合
• Sprinboot和Kafka的整合
• Kafka实战之削峰填谷
• 数据管道和流式处理(了解即可)

• Kafka实战之削峰填谷

《互联网大厂面试真题解析、进阶开发核心学习笔记、全套讲解视频、实战项目源码讲义》点击传送门即可获取！
轻大家的负担。**[外链图片转存中…(img-Dgh75lj6-1713460653445)]

[外链图片转存中…(img-x9lxng0u-1713460653446)]

[外链图片转存中…(img-x8XZM38c-1713460653446)]

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，基本涵盖了95%以上Java开发知识点，真正体系化！

由于文件比较大，这里只是将部分目录截图出来，每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频，并且会持续更新！

如果你觉得这些内容对你有帮助，可以扫码获取！！（备注Java获取）

Kafka实战笔记

关于这份笔记，为了不影响大家的阅读体验，我只能在文章中展示部分的章节内容和核心截图

[外链图片转存中…(img-NTxku2Zb-1713460653446)]

• Kafka入门
• 为什么选择Kafka
• Karka的安装、管理和配置

[外链图片转存中…(img-RGTjOWt8-1713460653447)]

• Kafka的集群
• 第一个Kafka程序
• [外链图片转存中…(img-0OYlvBGX-1713460653447)]

afka的生产者

[外链图片转存中…(img-0y03gaQP-1713460653447)]

• Kafka的消费者
• 深入理解Kafka
• 可靠的数据传递

[外链图片转存中…(img-HNnbLhCF-1713460653448)]

[外链图片转存中…(img-ct1A6yWh-1713460653448)]

• Spring和Kalka的整合
• Sprinboot和Kafka的整合
• Kafka实战之削峰填谷
• 数据管道和流式处理(了解即可)

[外链图片转存中…(img-Dwr8ZyTK-1713460653448)]

• Kafka实战之削峰填谷

[外链图片转存中…(img-3PsndmE6-1713460653448)]

《互联网大厂面试真题解析、进阶开发核心学习笔记、全套讲解视频、实战项目源码讲义》点击传送门即可获取！