统计学习——最小二乘法_最小二乘法例题

最小二乘法

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

法国数学家，阿德里安-马里·勒让德（1752-1833）提出让总的误差的平方最小的y就是真值，这是基于，如果误差是随机的，应该围绕真值上下波动。

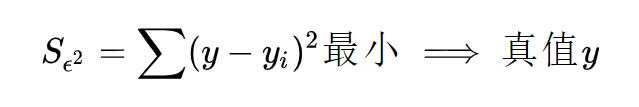
现在有多组观测值((x1,y1),(x2,y2),(x3,y3),…,(xn,yn)),可以带入上式，通过计算误差平方的最小值，求得这组观测值拟合的函数，这个函数既可以是一次函数y=ax+b，也可以是二元函数y=ax^2+bx+c,也可以是更高次数的函数。下面用一次函数y=ax+b举例：

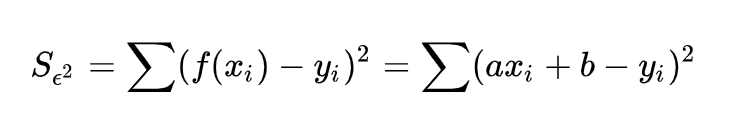
以上公式就是最小二乘法，所谓“二乘”就是平方的意思，台湾直接翻译为最小平方法。

推广

温度与冰淇淋的销量：

看上去像是某种线性关系：

可以假设这种线性关系为：

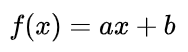
通过最小二乘法的思想：

上图的i,x,y分别为：

总误差的平方为：

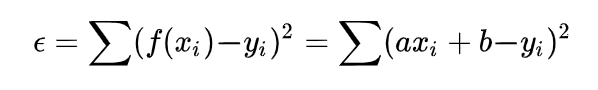
不同的a,b会导致不同的\epsilon，根据多元微积分的知识，当：

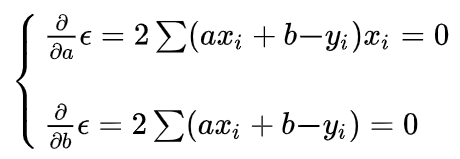
这个时候\epsilon取最小值。
对于a,b而言，上述方程组为线性方程组，用之前的数据解出来：

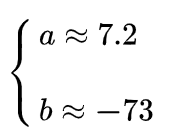
也就是这根直线：

其实，还可以假设：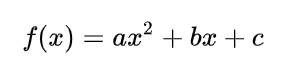
在这个假设下，可以根据最小二乘法，算出a,b,c，得到下面这根红色的二次曲线：

不同的数据，更可以选择不同的f(x)，通过最小二乘法可以得到不一样的拟合曲线：