- 1当"狂飙"的大模型撞上推荐系统
- 2seleniumbasic+VBA配置自动控制网页_vba selenium
- 3Python爬虫 利用百度翻译抓包实现查单词小工具(英翻中)_抓包软件抓包的字符怎么翻译
- 4flutter 数据储存的几种方式_flutter 存储数据
- 5esxi如何挂载物理机上的磁盘_ESXi 安装 macOS 虚拟机
- 6CSRF漏洞原理攻击与防御(非常细)_nginx 反向代理场景下如何 应对csrf 攻击
- 7水下机器人(rov)小知识(2)_水下机器人推进器分布
- 8IOS渲染流程之RenderServer处理图层信息_render service
- 9JLink不能识别CPU错误的解决办法: Could not find supported CPU core on JTAG chain
- 10大模型重构云计算:AI原生或将改变格局_大模型全方位重构云计算
自注意力机制(Self-Attention Mechanism)
赞
踩
自注意力机制(Self-Attention Mechanism)
一、什么是Self-Attention Mechanism
先让我们来了解什么是注意力机制,当我们看到一张图画时,第一眼肯定会注意到图片中最显眼的特征,**深度学习中的注意力机制(Attention Mechanism)**是一种模仿人类视觉和认知系统的方法,它允许神经网络在处理输入数据时集中注意力于相关的部分。通过引入注意力机制,神经网络能够自动地学习并选择性地关注输入中的重要信息,提高模型的性能和泛化能力。
例如下图:
我们大部分人第一眼注意到的一定是东方明珠,但是这图其实还有旁边的楼,下面的汽车等等。这其实就是一种Attention,我们关注的是最主要的东西,而刻意“忽视”那些次要的东西。
我们再来讲解一个重要的概念,即query、key和value。这三个词翻译成中文就是查询、键、值,看到这中文的意思,还是迷迷糊糊的。我们来举个例子:小明想在b站搜索深度学习,他把深度学习四个字输入到搜索栏,按下搜索键。搜索引擎就会将他的查询query映射到数据库中相关的标签key,如吴恩达、神经网络等等,然后向小明展示最匹配的结果value。

再比如以下这张图可以较好地去理解注意力机制,其展示了人类在看到一幅图像时如何高效分配有限注意力资源的,其中红色区域表明视觉系统更加关注的目标,从图中可以看出:人们会把注意力更多的投入到人的脸部。文本的标题以及文章的首句等位置。

自注意力机制(self-attention mechanism),也被称为注意力机制(attention mechanism),是一种用于序列数据建模的机制。它最初在自然语言处理领域中被广泛使用,但也可以应用于其他序列数据,如音频和时间序列数据。
自注意力机制的目标是对序列中的每个元素分配一个权重,以便根据元素之间的关系进行建模。它通过将输入序列中的每个元素与其他元素进行比较来实现这一点,然后为每个元素计算一个权重,表示该元素与其他元素的关联程度。这些权重可以用于加权聚合序列中的元素,以产生一个表示整个序列的上下文向量。
二、Self-Attention Mechanism的架构
原论文地址如下:Attention is All you Need (neurips.cc)
在原论文中我们可以看见这个公式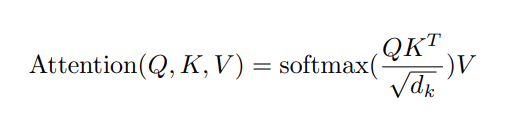 ,乍一看晦涩难懂,但是让我们一点一点来看,这个公式中的Q,K,V就是上面我们所描述的query、key和value
,乍一看晦涩难懂,但是让我们一点一点来看,这个公式中的Q,K,V就是上面我们所描述的query、key和value
1、计算过程
(1)定义输入
在进行Self - Attention之前,我们首先定义3个1×4的input。 pytorch代码如下:
import torch
x = [
[1, 0, 1, 0], # input 1
[0, 2, 0, 2], # input 2
[1, 1, 1, 1] # input 3
]
x = torch.tensor(x, dtype=torch.float32)
- 1
- 2
- 3
- 4
- 5
- 6
- 7

(2)初始化权重
每个input和三个权重矩阵分别相乘会得到三个新的矩阵,分别是key(橙色),query(红色),value(紫色)。我们已经令input的shape为1×4,key、query、value的shape为1×3,因此可以推出与input相乘的权重矩阵的shape为4×3。 代码如下:
import torch w_key = [ [0, 0, 1], [1, 1, 0], [0, 1, 0], [1, 1, 0] ] w_query = [ [1, 0, 1], [1, 0, 0], [0, 0, 1], [0, 1, 1] ] w_value = [ [0, 2, 0], [0, 3, 0], [1, 0, 3], [1, 1, 0] ] w_key = torch.tensor(w_key, dtype=torch.float32) w_query = torch.tensor(w_query, dtype=torch.float32) w_value = torch.tensor(w_value, dtype=torch.float32) print("Weights for key: \n", w_key) print("Weights for query: \n", w_query) print("Weights for value: \n", w_value)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
(3)计算key,query和value
现在我们计算key,query和value矩阵的值,计算的过程也很简单,运用矩阵乘法即可: key = input * w_key; query = input * w_query; value = input * w_value;
keys = x * w_key querys = x * w_query values = x * w_value print("Keys: \n", keys) # tensor([[0., 1., 1.], # [4., 4., 0.], # [2., 3., 1.]]) print("Querys: \n", querys) # tensor([[1., 0., 2.], # [2., 2., 2.], # [2., 1., 3.]]) print("Values: \n", values) # tensor([[1., 2., 3.], # [2., 8., 0.], # [2., 6., 3.]])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
(4)计算attention scores
例如:为了获得input1的注意力分数(attention scores),我们将input1的query(红色)与input1、2、3的key(橙色)的转置分别作点积,得到3个attention scores(蓝色)。 同理,我们也可以得到input2和input3的attention scores。
attn_scores = querys @ keys.T
print(attn_scores)
# tensor([[ 2., 4., 4.], # attention scores from Query 1
# [ 4., 16., 12.], # attention scores from Query 2
# [ 4., 12., 10.]]) # attention scores from Query 3
- 1
- 2
- 3
- 4
- 5
- 6
(5)对attention scores作softmax
上一步得到了attention scores矩阵后,我们对attention scores矩阵作softmax计算。softmax的作用为归一化,使得其中各项相加后为1。这样做的好处是凸显矩阵中最大的值并抑制远低于最大值的其他分量。
from torch.nn.functional import softmax
attn_scores_softmax = softmax(attn_scores, dim=-1)
print(attn_scores_softmax)
# tensor([[6.3379e-02, 4.6831e-01, 4.6831e-01],
# [6.0337e-06, 9.8201e-01, 1.7986e-02],
# [2.9539e-04, 8.8054e-01, 1.1917e-01]])
attn_scores_softmax = [
[0.0, 0.5, 0.5],
[0.0, 1.0, 0.0],
[0.0, 0.9, 0.1]
]
attn_scores_softmax = torch.tensor(attn_scores_softmax)
print(attn_scores_softmax)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
(6)将attention scores与values相乘
每个score(蓝色)乘以其对应的value(紫色)得到3个alignment vectors(黄色)。在本教程中,我们将它们称为weighted values(加权值)。
weighted_values = values[:,None] * attn_scores_softmax.T[:,:,None]
print(weighted_values)
- 1
- 2
(7)对weighted values求和得到output
从图中可以看出,每个input生成3个weighed values(黄色),我们将这3个weighted values相加,得到output(深绿)。图中一共有3个input,所以最终生成3个output。
outputs = weighted_values.sum(dim=0)
print(outputs)
# tensor([[2.0000, 7.0000, 1.5000], # Output 1
# [2.0000, 8.0000, 0.0000], # Output 2
# [2.0000, 7.8000, 0.3000]]) # Output 3
- 1
- 2
- 3
- 4
- 5
- 6
2、回到公式
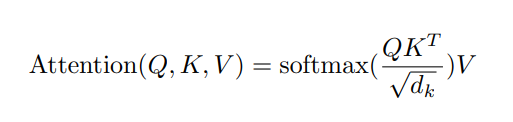
!
其实,这个公式就是描述了我们上面计算的过程。我们首先将
Q
u
e
r
y
与
K
e
y
的转置作点积,然后将结果除以
d
k
,再作
s
o
f
t
m
a
x
计算,最后将计算的结果与
V
a
l
u
e
作矩阵乘法得到
o
u
t
p
u
t
。
其实,这个公式就是描述了我们上面计算的过程。我们首先将Query与Key的转置作点积,然后将结果除以 \sqrt{d_k} ,再作softmax计算,最后将计算的结果与Value作矩阵乘法得到output。
其实,这个公式就是描述了我们上面计算的过程。我们首先将Query与Key的转置作点积,然后将结果除以dk
,再作softmax计算,最后将计算的结果与Value作矩阵乘法得到output。
这里有一个点,就是为什么要除以 d k ? d k 表示的是词向量的维度。我们除以 d k 是为了防止 Q K T 值过大,导致 s o f t m a x 计算时上溢出 ( o v e r f l o w ) 。其次 , 使用 d k 可以使 Q K T 的结果满足期望为 0 ,方差为 1 的分布。 这里有一个点,就是为什么要除以 \sqrt{d_k}? d_k表示的是词向量的维度。我们除以d_k是为了防止 QK^T值过大,导致softmax计算时上溢出(overflow)。其次,使用 d_k可以使QK^T的结果满足期望为0,方差为1的分布。 这里有一个点,就是为什么要除以dk ?dk表示的是词向量的维度。我们除以dk是为了防止QKT值过大,导致softmax计算时上溢出(overflow)。其次,使用dk可以使QKT的结果满足期望为0,方差为1的分布。
3、为什么这样计算
最后的问题是,为什么要像公式那样计算呢?
我们先从
Q
K
T
QK^T
QKT
看起,从几何角度看,点积是两个向量的长度与它们夹角余弦的积。如果两向量夹角为90°,那么结果为0,代表两个向量线性无关。如果两个向量夹角越小,两向量在方向上相关性也越强,结果也越大。点积反映了两个向量在方向上的相似度,结果越大越相似。

对
Q
K
T
进行相似度的计算后,再使用
s
o
f
t
m
a
x
归一化。最后将归一化的结果与
V
作乘法,计算的结果就是输入经过注意力机制加权求和之后的表示。
对QK^T进行相似度的计算后,再使用softmax归一化。最后将归一化的结果与V作乘法,计算的结果就是输入经过注意力机制加权求和之后的表示。
对QKT进行相似度的计算后,再使用softmax归一化。最后将归一化的结果与V作乘法,计算的结果就是输入经过注意力机制加权求和之后的表示。
三、简单代码实现
import torch import torch.nn as nn class SelfAttention(nn.Module): def __init__(self, input_size, hidden_size): super(SelfAttention, self).__init__() self.input_size = input_size self.hidden_size = hidden_size self.query = nn.Linear(input_size, hidden_size) self.key = nn.Linear(input_size, hidden_size) self.value = nn.Linear(input_size, hidden_size) self.softmax = nn.Softmax(dim=1) def forward(self, x): q = self.query(x) k = self.key(x) v = self.value(x) # 计算注意力权重 scores = torch.matmul(q, k.transpose(1, 2)) attention_weights = self.softmax(scores) # 上下文向量计算 context_vector = torch.matmul(attention_weights, v) return context_vector, attention_weights # 测试自注意力机制 input_size = 4 hidden_size = 5 x = torch.randn(3, 10, input_size) # 输入序列的维度为(序列长度, 批量大小, 输入特征数) self_attention = SelfAttention(input_size, hidden_size) context_vector, attention_weights = self_attention(x) print("Context vector:\n", context_vector) print("Attention weights:\n", attention_weights)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
在这个示例中,我们定义了一个名为SelfAttention的自注意力机制类,它包括查询(query)、键(key)和值(value)的线性变换层,以及一个softmax函数用于计算注意力权重。在forward方法中,我们将输入序列x通过查询、键和值的线性变换层得到对应的向量,然后计算注意力权重。最后,我们将注意力权重与值向量相乘,得到上下文向量context_vector,并返回它以及注意力权重attention_weights。
在代码的末尾,我们使用一个随机生成的输入序列x进行了简单的测试。输入序列的维度为(序列长度, 批量大小, 输入特征数),这里我们假设序列长度为10,批量大小为3,输入特征数为4。然后,我们创建了一个SelfAttention实例,并将输入序列传递给它的forward方法,得到上下文向量和注意力权重。最后,我们打印出上下文向量和注意力权重的值。
此文章仅作为学习笔记使用
参考:动图轻松理解Self-Attention(自注意力机制) - 知乎 (zhihu.com)
x进行了简单的测试。输入序列的维度为(序列长度, 批量大小, 输入特征数),这里我们假设序列长度为10,批量大小为3,输入特征数为4。然后,我们创建了一个SelfAttention实例,并将输入序列传递给它的forward方法,得到上下文向量和注意力权重。最后,我们打印出上下文向量和注意力权重的值。**
此文章仅作为学习笔记使用




