　　斐波那契数列的发明者，意大利数学家列昂纳多·斐波那契（Leonardo Fibonacci），生于公元1170年，卒于1250年，籍贯是比萨。他被人称作“比萨的列昂纳多”。

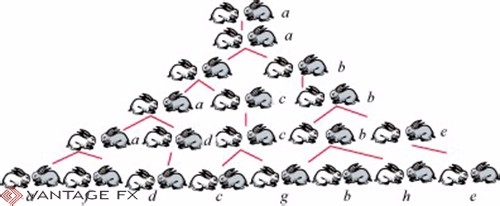
　　列昂那多·斐波那契于1202年研究兔子产崽问题时发现了此数列。设一对大兔子每月生一对小兔子，每对新生兔在出生一个月后又下崽，假若兔子都不死亡。问：一对兔子一年能繁殖成多少对兔子？

　　题中本质上有两类兔子：一类是能生殖的兔子，为大兔子；新生的兔子不能生殖，为小兔子；小兔子一个月就长成大兔子，求的是大兔子与小兔子的总和？
　　十二月时有大兔子144对，小兔子89对，共有兔子144+89=233对

从上表看出：

　　①每月小兔对数=上月大兔对数

　　②每月大兔对数等于上个月大兔对数与小兔对数之

综合①②两点可得：每月大兔对数等于前两个月大兔对数之和　　如果用un表示第n月的大兔对数，则有un=un-1+un-2(n > 2)

　　每月大兔对数un排成数列为：1、1、2、3、5、8、13、21、34、55、89、144…

　　那么此组数列就称为斐波那契数列

END

斐波那契数列通项公式

递推公式：

　　斐波那契数列：0、1、1、2、3、5、8、13、21、34、55、89、144…

如果设F(n)为该数列的第n项(n∈N*)，那么这句话可以写成如下形式：显然这是一个线性递推数列。

通项公式：
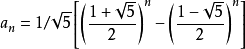
此公式又称为“比内公式”，是用无理数表示有理数的一个范例。

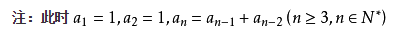
解法1：非数组+非递归


#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a,b,c;
 
int main()
{
	a=1;
	b=1;
	for(int i=1;i<=38;i++)//38的原因是已知两个数的值 
	{
		c=a+b;//前一个值+前两个值
		a=b;//值位置的变换 
		b=c;
	}
	printf("%lld",c);
	return 0; 
}

解法2：数组+非递归

时间复杂度约为O（n）


#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=41;
ll num[maxn];
 
int main()
{
	num[1]=1;
	num[2]=1;
	for(int i=3;i<=40;i++)
	{
		num[i]=num[i-1]+num[i-2];
	}
	printf("%d",num[40]);
	return 0;
}

解法3：非数组+递归

时间复杂度约为（2^n）


#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll step=0,cnt=0;
 
int Digui(ll step)
{
	cnt++;
	if(step==1||step==2)
	{
		return 1;
	}
	return Digui(step-1)+Digui(step-2);
}
 
int main()
{
	Digui(40);
	printf("%lld\n%lld",Digui(40),cnt);//答案 递归次数 
	return 0;
}

通过cnt计算发现，进行了非常多次数的递归，原因是我们进行了重复计算

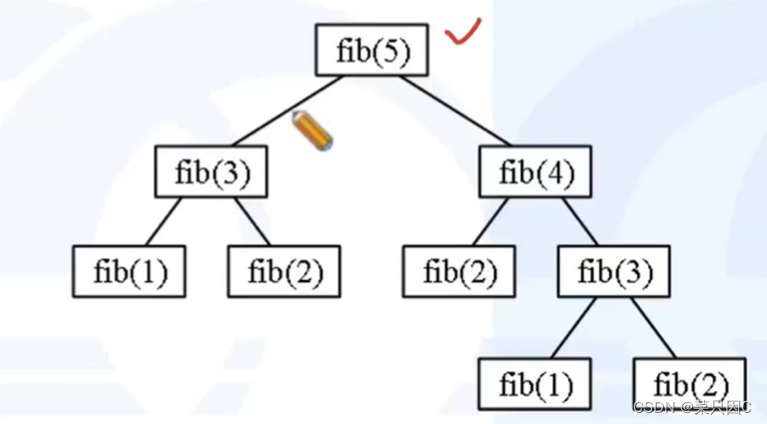
这样二叉树的结构导致进行了大量重复计算，这是我们特别不希望看到的，所以要进行记忆化

解法4：数组+递归


#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=41;
ll num[maxn];
ll step=0,cnt=0;
bool vis[maxn];
int Digui(ll step)
{
	cnt++;
	if(step==1||step==2)
	{
		return 1;
	}
	if(!vis[step])
	{
		vis[step]=true;
		num[step]=Digui(step-1)+Digui(step-2);
		return num[step];
	}
	else
	{
		return num[step];
	}
}
int main()
{
	vis[1]=true;
	vis[2]=true;
	num[1]=1;
	num[2]=1;
	Digui(40);
	printf("%lld\n%lld",Digui(40),cnt); 
	return 0;
}

这样计算次数会大大降低

7 补充：蓝桥杯简介

一. 蓝桥杯赛事简介

蓝桥杯全国软件和信息技术专业人才大赛，是由工业和信息化部人才交流中心举办的全国性IT学科赛事。全国1200余所高校参赛，累计参赛人数超过40万人。蓝桥杯大赛连续两年被列入中国高等教育学会发布的“全国普通高校学科竞赛排行榜”，是高校教育教学改革和创新人才培养的重要竞赛项目。对大学生综合评测，奖学金评定，升学考研都有一定助益。

大赛共包括三个竞赛组别，个人赛-软件类，个人赛-电子类，以及视觉艺术大赛。其中个人赛-软件类的比赛科目包括C/C++程序设计、Java软件开发、Python程序设计。今年第十二届蓝桥杯报名时间是2020年12月-2021年3月，4月省赛，5月国赛。

蓝桥杯大赛已成功举办11届，成为国内始终领跑的人才培养选拔模式，并受到行业和企业的高度认可，含金量也逐年增加，主要体现在：

蓝桥杯大赛题目的专业度高，专业度和难度已经与国际国内知名程序设计类竞赛不相上下。

双一流大学的参与度逐年提高，以最近的第11届蓝桥杯大赛为例，来自双一流大校的参赛选手近10000名；

专业顶尖选手越来越多，对历年选手的跟踪回访，发现大赛选手与ACM参赛选手高度重叠，可谓赢家通吃。

二. 参加蓝桥杯的好处

大学，是人生中最美最重要的时段。在大学，有的人经历苍白，有的人经历丰富，究竟是苍白还是丰富，取决于人的选择。如果你是IT类的学生，那么，我建议你了解并参加蓝桥杯大赛。既然我这么建议，那肯定是有道理的，比如：

1. 可以丰富自己的大学经历

有的人，在大学失去了方向和斗志，浑浑噩噩，当初信誓旦旦要从事IT相关领域，最后发现，是从事打游戏这个领域，毕业前才发现，自己所学甚少。而蓝桥杯大赛，恰好可以让你丰富自己的大学经历，不枉费专业，不虚此行。

2. 可以提供自己的实力和水平

有不少同学是很有上进心的，但苦于不知道怎么发力。那么，蓝桥杯大赛，能给你指引好方向，让你处在竞争的氛围中，牵引着你向前。通过大赛实战，不断地检验和完善自己，经历挫败和曲折后，获得成功，这种经历，尤为珍贵。

3. 可以为将来的职业铺好道路

大家都是要去求职的，在面试中，最忌讳的就是，拿不出曾经的经历和成绩，无法打动面试官和公司。有的人在面试时，只说自己爱好学习，但拿不出任何证据。相反，如果参加蓝桥杯这样的大赛，成功也好，失败也好，至少来讲，你比别人多了一块敲门砖，面试官也会对你刮目相看。

三. 蓝桥杯的备战攻略

蓝桥杯大赛，含金量在不断上升，参与的人数也在逐渐增多。前面说了，蓝桥杯大赛是个人赛，相对来说参加门槛低，分组的赛制对参赛选手也更加友好。但是，这并不意味着你可以高枕无忧。毕竟，没有人能随随便便成功。攻略和建议如下：

第一，当然是报名啦。有的朋友，准备得很充分，准备上战场的时候，才发现忘了报名或者错过报名时间。如果院校不组织参加，自己也可以选择个人报名，千万别忘记到官网报名。否则一失足成心头恨，再回首已是深秋。

第二，要充分掌握竞赛设涉及到的一些语言，熟练使用一些API, 这些东西，并不需要你死记硬背(比赛会提供相关的API说明)，但肯定要有一个大概的印象。

第三，算法很重要，很重要，很重要。自己平时可以多找一些算法相关的书籍看看，对常用常见常考的算法，做到了如指掌，这样才能才大赛时随机应变。

第四，搞懂了基本的算法之后，还得实战，那就要大量刷题，刷题，刷题。蓝桥杯大赛官网有历年真题，只有通过大量刷题，才能举一反三，触类旁通，即使大赛遇到陌生题目，也不担心。

四. 关于蓝桥杯的结语

人生本来就是各种经历，大学是人生中最美好的阶段，对于身处IT浪潮中的同学而言，愿大家不负韶华，珍惜机会，丰富经历。希望有志青年，在蓝桥杯大赛中，碰撞出璀璨的智慧火花。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/434143