- 1什么是人工智能领域的强化学习?_强化学习 是人工智能
- 2Python免费下载安装全流程(Python 最新版本),新手小白必看!_python下载教程
- 3借助 Keras 3 轻松上手 Gemma 模型
- 4动态规划经典例题二_int nposition = distance(label.begin(), ret);
- 5AI 技术在前端开发流程中如何应用??3分钟带你一览开放原子开发者大会 OpenTiny 最新资讯!
- 6基于Nacos+SpringCloudAlibaba的服务治理
- 7动态规划-二维dp数组和滚动数组_滚动数组dp
- 8【网络编程】——基于TCP协议实现回显服务器及客户端_回显实验tcp_echoserver_accept
- 9亿某通电子文档安全管理系统 hiddenWatermark/uploadFile 文件上传漏洞_北京亿赛通数据泄露漏洞
- 10mybatis mysql 多租户_MyBatis利用MyCat实现多租户的简单思路分享
十四. 四轮车驱动开发之五: 由浅至深理解6轴陀螺仪姿态解算算法<下>_六轴陀螺仪数据
赞
踩
十二.四轮车驱动开发之五: 由浅至深理解6轴陀螺仪姿态解算算法(上)
十三.四轮车驱动开发之五: 由浅至深理解6轴陀螺仪姿态解算算法(中)
十四.四轮车驱动开发之五: 由浅至深理解6轴陀螺仪姿态解算算法(下)
由浅至深理解6轴陀螺仪姿态解算算法 <下篇>:
五.对算法中关键知识点进行重点讲解
1. 关键知识点1: 当前姿态四元数q(参考坐标n系)算出重力在三个轴上的分量(载体坐标b系)
2. 关键知识点2: 用两个向量叉积(也叫向量积,外积),来表示载体坐标系角速度分量误差error
3. 关键知识点3: 四元数微分方程,一阶毕卡解法,融合修正后陀螺仪姿态到当前四元数q中
4. 关键知识点4: 把用四元数q表示的姿态转化为用欧拉角表示的姿态
首先,把前面算法流程框图重新发一下,,然后在对算法中4个关键知识点,逐一攻克:

五.对算法中关键知识点进行重点讲解
1. 关键知识点1: 从当前姿态四元数q(参考坐标n系)计算出重力在三个轴上的分量(载体坐标b系)
参考前面公式(11) 和 公式(28)中![]() 的转置矩阵(因为下面代码需要从n坐标系-->b坐标系系)
的转置矩阵(因为下面代码需要从n坐标系-->b坐标系系)
- //用当前姿态(参考坐标n系)计算出重力在三个轴上的分量(载体坐标b系),
- /*把四元数换算成"方向余弦矩阵"中的第三列的三个元素.根据余弦矩阵和欧拉角的定义,地理坐标系的重力向量,转到载体坐标系,正好是这三个元素.*/
- posture_x = 2*(q1q3 - q0q2);
- posture_y = 2*(q0q1 + q2q3);
- posture_z = q0q0 - q1q1 - q2q2 + q3q3;
2. 关键知识点2: 用两个向量叉积(也叫向量积,外积),来表示载体坐标系角速度分量误差error
先说明下算法两类参数意义:
ax,ay,az: 表重力加速度在载体坐标系Oxyz三轴的加速度分量,单位: m/s^2;
gx,gy,gz: 表载体围绕载体坐标系Oxyz三轴的旋转角速度,单位: rad/s, 弧度/秒.
以下仅以x轴方向的重力分量ax和角速度gx做分析:
根据算法中代码:
- // adjusted gyroscope measurements
- gx = gx + Kp*error_x + xErrorInt;
- gy = gy + Kp*error_y + yErrorInt;
- gz = gz + Kp*error_z + zErrorInt;
可知: error_x 和xErrorInt应该与gx具有类似的单位rad/s,考虑到对gx和error_x累加积分, error_x 和xErrorInt也至少应该是个弧度值.
好了,明确了error_x 和xErrorInt的单位,我们就可以进一步更精准确定它们的意义:
error_x: 应为载体坐标系在x轴上当前时刻较上一时刻的旋转弧度偏差(网上很多代码翻译为误差,容易误导);
xErrorInt: 上述弧度偏差error_x的比例积分, 就是载体坐标系在到当前时刻为止累积的偏差和.
问题在于这个弧度偏差error_x,如果通过前后两个时刻加速度计分量来计算?
根据加速度计和陀螺仪的特性: 长期加速度计可信度高,短期陀螺仪可信度高;
所以计算过程就是: 对加速度计的每次测量结果进行偏差后进行比例累加,对当前陀螺仪单次结果直接信任相加.
好,下面来看计算偏差的代码. 代码中英文翻译应该就是原作者的注释:
- // Error is sum of cross product between estimated and measured direction of gravity
- error_x = (ay*posture_z - az*posture_y) ;
- error_y = (az*posture_x - ax*posture_z) ;
- error_z = (ax*posture_y - ay*posture_x) ;
对于第一行: error_x = (ay*posture_z - az*posture_y) ; 怎么理解呢?
如图所示:
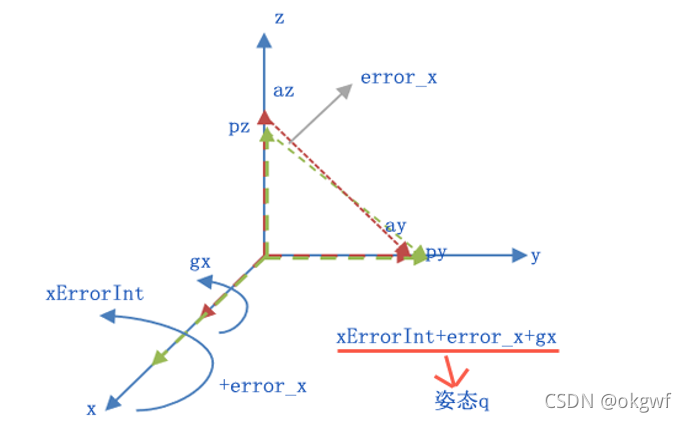
加速度计本次测量的重力在载体坐标系Oxyz的y和z轴的分量向量为: (ay,0)和(0, az)
从载体当前姿态计算出来的重力在载体坐标系Oxyz的y和z轴的分量向量为: (py,0)和(0, pz)
向量az_ay = (ay,0) - (0, az) = (ay,-az)
向量pz_py = (py,0) - (0, pz) = (py,-pz)
两个向量的叉积: az_ay X pz_py = (ay,-az) X (py,-pz) = -ay*pz – (-az*py) = -(ay*pz - az*py)
因为表示的是偏差,正负值就是表示偏差角度的方向,改变方向保持和陀螺仪一致,可以去掉负号;
az_ay X pz_py = ay*pz - az*py = |az_ay| * |pz_py| * sinθ
可见当算法执行周期特别短, 向量az_ay和向量pz_py偏差角度特别小时,再加上参与计算是归一化向量本身值比较小,所有有:
error_x = ay*pz - az*py = |az_ay| * |pz_py| * sinθ ≈ sinθ ≈ θ
这在一定程度上反应了两个向量的不平行度,甚至可以直接用两个向量的叉积来表示两个向量的夹角值.
当两个向量平行时,θ=0, error_x = 0, 这是我们完全相信gx,gx为Ox轴旋转角速度,瞬时时刻就是陀螺仪测量的载体绕Ox轴旋转偏差; 然后gx和Kp*error_x,xErrorInt一起计入累计旋转角度值;
当两个向量不平行时,θ>0, error_x > 0, 这是我们仍坚信gx,并和Kp*error_x,xErrorInt一起计入累计旋转角度值.
error_y和error_z类似.
3. 关键知识点3: 四元数微分方程,一阶毕卡解法,融合修正后陀螺仪姿态到当前四元数q中
这里用到三个数学概念,这里不再详细阐述:
- 微积分的泰勒公式;
- 四元数微分方程,证明过程请自行百度;
- 毕卡逼近法求解精确值.
- 泰勒公式:
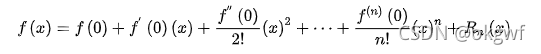
- 四元数微分方程:
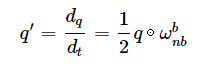 这里q是算法中姿态四元数q(q0,q1,q2,q3),
这里q是算法中姿态四元数q(q0,q1,q2,q3), ![]() 为陀螺仪测测量值,即算法中修正后的[0,gx,gy,gz]^T.
为陀螺仪测测量值,即算法中修正后的[0,gx,gy,gz]^T.
- 毕卡逼近法:
(略,不作阐述)
(1).先从四元数微分方程开始
从前面已经证明的四元数乘法结论公式(22): q☉r = M(q)r = M’(r)q
得:  <1>
<1>
进一步有:
 <2>
<2>
由于陀螺仪测测量值(修正后)![]() =[0,gx,gy,gz]^T单位是rad/s是个角速度值,即瞬时弧度变化值, 所以上面公式得到的只是q的瞬时变化值Δq. 要把这个瞬时Δq加到现有的q中,才能更新现有姿态.
=[0,gx,gy,gz]^T单位是rad/s是个角速度值,即瞬时弧度变化值, 所以上面公式得到的只是q的瞬时变化值Δq. 要把这个瞬时Δq加到现有的q中,才能更新现有姿态.
(2). 使用毕卡逼近法计算相邻时刻的四元数值
四元数微分方程的毕卡逼近法,表达如下:
 <3>
<3>
这里:
q_k和q_k+1: 均是四元数的列向量形式;
I: 单位方阵;
Δθ_k: k时刻角度变化值,其实就是上面![]() _k;
_k;
Δθ: 是k+1时刻角度变化值,即当前时刻值![]() _k+1=[0,gx,gy,gz]^T, 如下:
_k+1=[0,gx,gy,gz]^T, 如下:
 <4>
<4>
公式3中,设C = 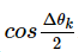 , S =
, S = .
.
将C,S中的三角函数按照泰勒公式级数展开,取前三项,得:
| n | 1 | 2 | 3 |
| C_n | 1 | 1-(Δθ_k)^2/8 | 1-(Δθ_k)^2/8 |
| S_n | 1/2 | 1/2 | 1/2 -(Δθ_k)^2/48 |
上表中取泰勒公式级数的一级近似,带入上面公式<3>,可得四元数微分方程的一阶近似公式为:
 <5>
<5>
最终,我们回到6轴陀螺仪算法中, 对记录当前姿态的四元数q(q0,q1,q2,q3)进行更新时,代入上面公式<5>:
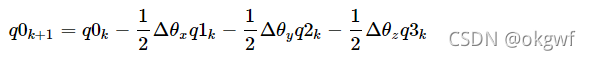
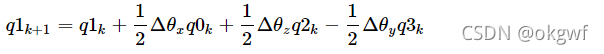
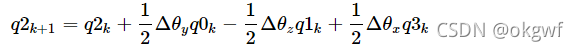
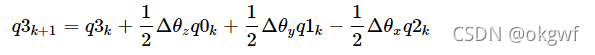
根据上面的结论,有q_k和当前修正过的gx,gy,gz.就可以实现我们的关键知识点<3>,四元数微分方程,一阶毕卡解法,融合修正后陀螺仪姿态到当前四元数q中, 代码如下:
- //四元数微分方程. 采用一阶毕卡解法,融合当前位姿和陀螺仪测量值,并转换到世界参考坐标系N.
- q0 = q0temp + (-q1temp*gx - q2temp*gy -q3temp*gz)*halfT;
- q1 = q1temp + (q0temp*gx + q2temp*gz -q3temp*gy)*halfT;
- q2 = q2temp + (q0temp*gy - q1temp*gz +q3temp*gx)*halfT;
- q3 = q3temp + (q0temp*gz + q1temp*gy -q2temp*gx)*halfT;
4. 关键知识点4: 把用四元数q表示的姿态转化为用欧拉角表示的姿态
参考公式(28)和公式(29),代码如下
- //四元数到欧拉角的转换,这里输出的是弧度,想要角度值,可以直接乘以57.3,即一弧度对应角度值
- angle->roll = atan2f(2.f * (q0q1 + q2q3),1 - 2.f * ( q1q1 - q2q2) ); // roll: X轴
- angle->pitch = asinf(2.f * (q0q2 - q1q3) ); // pitch: Y轴
- //其中YAW航向角由于加速度计对其没有修正作用,因此实际结果会逐渐偏移,想要准确,需要使用磁力计
- angle->yaw = atan2f(2.f * (q0q3 + q1q2),1 - 2.f * (q2q2 + q3q3) ); // yaw: Z轴
-
- /*
- Note: 上面的代码,其实有个问题,就是该代码是针对飞行器导航设计的,其前后纵向轴为载体坐标系Oxyz
- 的x轴,而不是陆地四轮车那样前后纵向轴为载体坐标系Oxyz的y轴.但不要担心, 学习了本文后,
- 你也可以动手修改它.
-
- 朋友,请自行修改吧.
- */
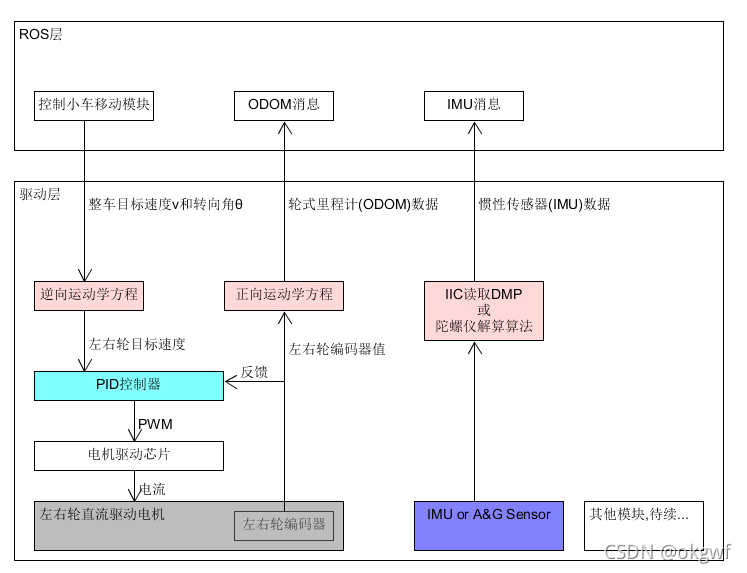
最后,同样上传一张从ROS系统和驱动控制板整体看的相关框架图: