【考研数学】五. 二重积分_二重积分r方×r

五. 二重积分

基础知识点1：二重积分的概念

∫∫ 积分区域

f（x,y）被积函数 dxdy

基础知识点2：被积函数为1时，二重积分的意义

积分区域的面积

基础知识点3：二重积分的计算方法

如果积分区域D是“⚪”相关的，则使用极坐标系法来计算，否则就使用直角坐标系进行计算。而直角坐标系可分为 先x后y 或者 先y后x 法。从几何直觉来说，先对y积分可以先考虑。

极坐标系方法：

1. 画积分区域D的图
2. 将二重积分改写（极坐标或直角坐标） 累次积分计算
3. 换被积函数，再被积函数中乘ρ
4. 确定积分上下限
5. 计算

直角坐标方法：

1. 画图
2. 换积分
3. 算上下限
4. 计算

如果是极坐标求r的上下限，通过x = rcos θ 以及 y = r sin θ 代入到 对应的 曲线方程中即可。（找到线段的最近 | 最远 的交点的曲线）

基础知识点4： 二重积分的三条性质

性质1：二重积分内的被积函数，出现常数a，a可以提出。

性质2：被积函数可拆成多项相加。

性质3：积分区域可拆成多项相加

设积分连续，求二次积分的值，若出现对称，可以消去。

核心考点1：二重积分是一个常数

3 + 二重积分 = f（x，y） ， 那么f（x,y）是常数

核心考点2： 含绝对值的二重积分计算

令绝对值里面的东西为0，解出一条线，然后用那条线去拆分积分区域D

核心考点3：二重积分的对称性

• 若积分区域D关于x轴对称
  • 若f(x,y)对 y 为奇函数，则二重积分∫∫f（x,y）dxdy = 0
  • 若f(x,y)对 y 为偶函数，则二重积分在D区域的∫∫f（x,y）dxdy = 2倍单侧D1 f（x,y）dxdy
• 若积分区域D关于y轴对称
  • 若f(x,y)对 x 为奇函数，则二重积分∫∫f（x,y）dxdy = 0
  • 若f(x,y)对 x 为偶函数，则二重积分在D区域的∫∫f（x,y）dxdy = 2倍单侧D1 f（x,y）dxdy 、

核心考点4：二重积分的轮换对称性

任何一个二重积分都可以用轮换对称性

被积函数 && 积分区域中的x，y互换，新得到的二重积分与原二重积分相等。

类似下图：

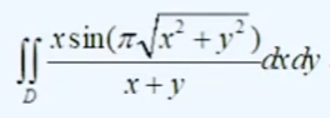
若被积函数是一个分数，分母中x,y可以互换，积分区域中xy也对称，则可以使用轮换对称性。相加两次求两倍的二重积分和，最后除2即可。

核心考点5：交换积分次序

只需要将四条线围成的图画出来即可。

后面积分的是数值，先积分的可能是包含后积分的函数

若考研中已经给出了对x和对y的积分，且告诉了上下限，则需要交换积分次序。

不一定是一上来就直接交换积分次序，可能只是分段交换。

核心考点6： 形心

变形技巧：

如果出现了从0到Π，分子有x，主体函数都是三角函数，使用Π - x 换元。