【Matlab】建立最优控制LQR控制器模型_lqr控制算法matlab

前言

之前做了有关于系统辨识以及配置极点来控制系统响应的相关内容，那些相当于是打开了一个新世界的大门，在此基础上，一直想学习一下最优控制的相关内容，并应用在项目上，因此，学习了相当长的时间，然后搭建模型，不过越来越感到，我学习到的也只是控制世界的冰山一角，话不多说，开始记录搭建模型的步骤。

传递函数转化到状态空间

首先，我可以辨识出系统的传递函数，需要转化成状态方程，这里我稍微记录了一下由传递函数转换到状态空间的步骤：

以上是随便举了一组数据手算的，之后使用Matlab验证，Matlab是有这种转换函数可以直接调用的：

%*************************************************************************%
                %传递函数转化为状态方程
%**********************************************************************%
 
num = [4,9,14,23];
den = [2,4,6,10];
sys = tf(num,den);   %转化为传递函数G
 
[A,B,C,D]=tf2ss(num,den); %传递函数转化为状态空间

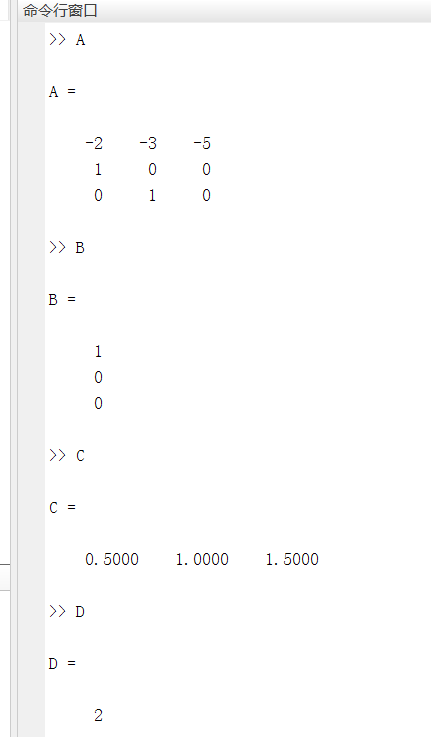
可以看到，与我实际计算出来的是吻合的。当然，如果能够直接建立微分方程的模型，就不需要此步骤了。

建立观测器

接下来，需要建立状态观测器，因为实际的状态变量x，并不容易被测量，或者说，有时候由传递函数转化到状态空间之后，x代表的状态是对应不到实际的物理意义的，因此观测器的设计还是很有必要，这里我参考学习了一些全阶观测器的设计过程，步骤如下：

1.建立状态方程与估计方程：

2.求出状态与估计状态之差的通式

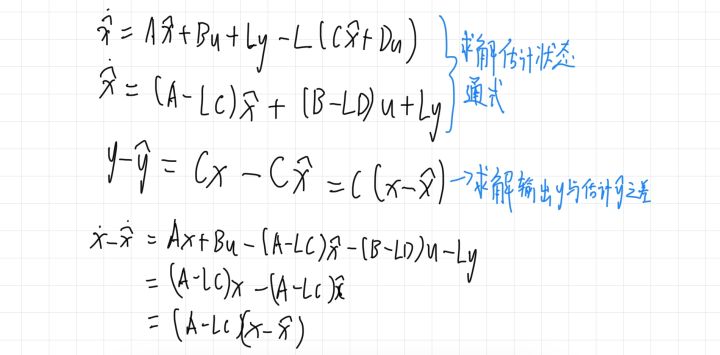
3.引入状态误差变量，求出其特征值，即可得出状态观测器L矩阵的元素值

例：

总体步骤：

求解全阶观测器L矩阵在Matlab也是直接有函数可以计算的，上述的手算过程只是为了来练习一下，了解观测器的原理与步骤。程序如下：

%*************************************************************************%
                %计算全阶观测器矩阵L的参数
%**********************************************************************%
 
%输入状态方程矩阵
A = [0 1;-1 -0.5];
B = [0;1];
C = [1 0];
D = 0;
 
%输入观测器期望极点 即特征值
V = [-1 -1];
 
L = (acker(A',C',V))';
L =
    1.5000
   -0.7500

建立simulink仿真：

我在积分环节那里设置了初始值，就是为了让实际状态与估计状态初始不一样，这样可以看到收敛效果，从上图中可以看出估计值最终收敛，与实际状态x重合。

求解控制律U

这里设控制律U = -K * X + e ，K即为空置率矩阵，X为状态矩阵，e为目标值与实际值的误差(为了加入跟随性能)

具体求解最优控制率U的问题，设计泛函分析与极小值原理等等，这个我只是看了一部分书上的东西，在没有自己琢磨好之前，还是先留着，以后自己验算完成再发。

因此我就省事了一下，直接用Matlab求解K矩阵。上面那个系统的参数有些简单，为了验证效果，我把传递函数取了一些奇怪的数字：

%*************************************************************************%
                %传递函数转化为状态方程
%**********************************************************************%
 
num = [0 333.1 279.9 358.1];
den = [1 0.5404 0.05445 0];
sys = tf(num,den);   %转化为传递函数G
 
[A,B,C,D]=tf2ss(num,den); %传递函数转化为状态空间
 
A =
 
   -0.5404   -0.0544         0
    1.0000         0         0
         0    1.0000         0
 
B =
 
     1
     0
     0
 
C =
 
  333.1000  279.9000  358.1000
 
D =
 
     0

可以看到这个系统的矩阵略微复杂了一些，真实的系统参数应该就是这样比较难算的，这里还是得感谢Matlab这个工具，帮我省略了一大波计算过程，我可以直接得到观测器矩阵L的值：

%根据观测器的期望极点计算观测器L矩阵
L = (acker(A',C',V))';
 
 
L =
 
    0.9697
    0.1769
   -0.9733

以及得到控制律矩阵K的值：

%指定QR矩阵，计算控制率
Q = [100,0,0;0,1,0;0,0,1];
R = 0.2;
 
K = lqr(A,B,Q,R);   %输出LQR控制器的K矩阵
 
 
>> K
K =
 
   22.2824   10.2930    2.2361

画出Simulink模型：

这里的控制器U的状态输入是使用估计状态 xhat，实际项目中也会是使用估计值。

在simulink设置中设置计算步长：

可以看到观测器的收敛效果以及输出量的跟随效果。点个赞喽！