c语言实现二叉树(链式结构)_编写c或c++语言程序,利用链式存储的方式来实现下列功能: (1)采用二叉树性质5来建

---

前言

当我们使用顺序结构实现了二叉树的存储后，接下来就是使用链式结构来实现二叉树的存储。

一、二叉树的遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

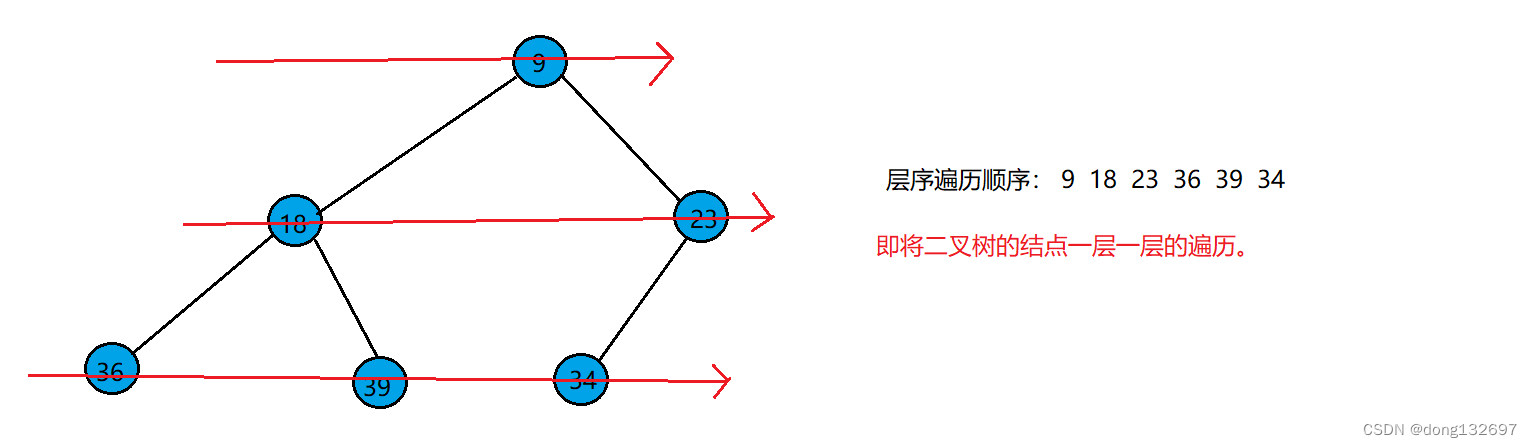
1、二叉树的层序遍历

二叉树的层序遍历在前面介绍二叉树的顺序结构存储时，已经使用到了，即完全二叉树在数组中的存储顺序就是该二叉树的层序遍历顺序。

2、二叉树的前序遍历

前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。#号表示空树的位置。

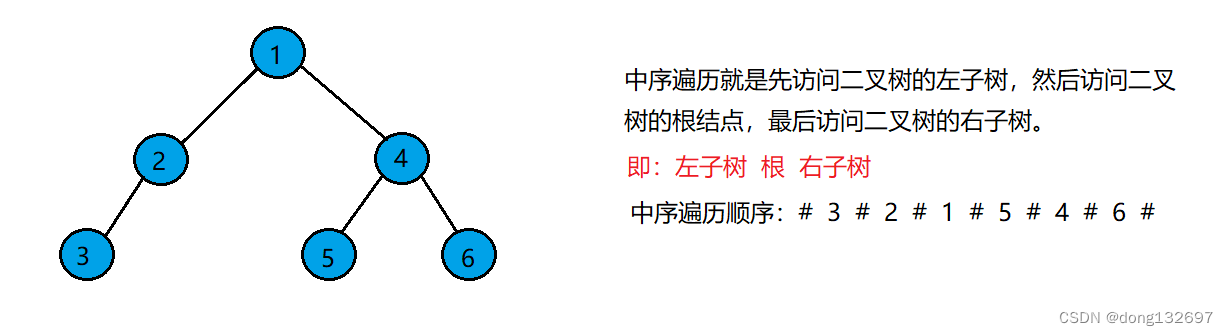
3、二叉树的中序遍历

中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。#号表示空树的位置。

4、二叉树的后序遍历

后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。#号表示空树的位置。

5、代码实现

知道了二叉树的前、中、后序遍历的规则后，我们就可以实现一个二叉树，然后实现这些遍历方法。
二叉树定义

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<errno.h>

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	//存储该结点的左子树的根结点地址
	struct BinaryTreeNode* left;
	//存储该结点的右子树的根结点地址
	struct BinaryTreeNode* right;
	//存储该结点的数据
	BTDataType data;
}BTNode;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

创建二叉树结点

//创建一个新的结点，并且将该结点返回
BTNode* BuyNode(BTDataType x)
{
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newNode->left = NULL;
	newNode->right = NULL;
	newNode->data = x;
	return newNode;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

创建一棵二叉树

//创建一棵二叉树，并且返回该二叉树的根结点
BTNode* CreateBinaryTree()
{
	//建立二叉树的结点
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	//建立二叉树结点之间的关系
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	//返回该二叉树的根结点
	return node1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

实现先序遍历

//先序遍历
void PreOrder(BTNode* root)
{
	//如果访问的结点为NULL，就打印#
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	//如果访问结点不为NULL，就将该结点的数据打印出来
	printf("%d ", root->data);
	//因为为先序遍历，所以先访问根节点，然后再访问左子树
	PreOrder(root->left);
	//当左子树访问完再访问右子树
	PreOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

即函数递归调用的顺序如图。

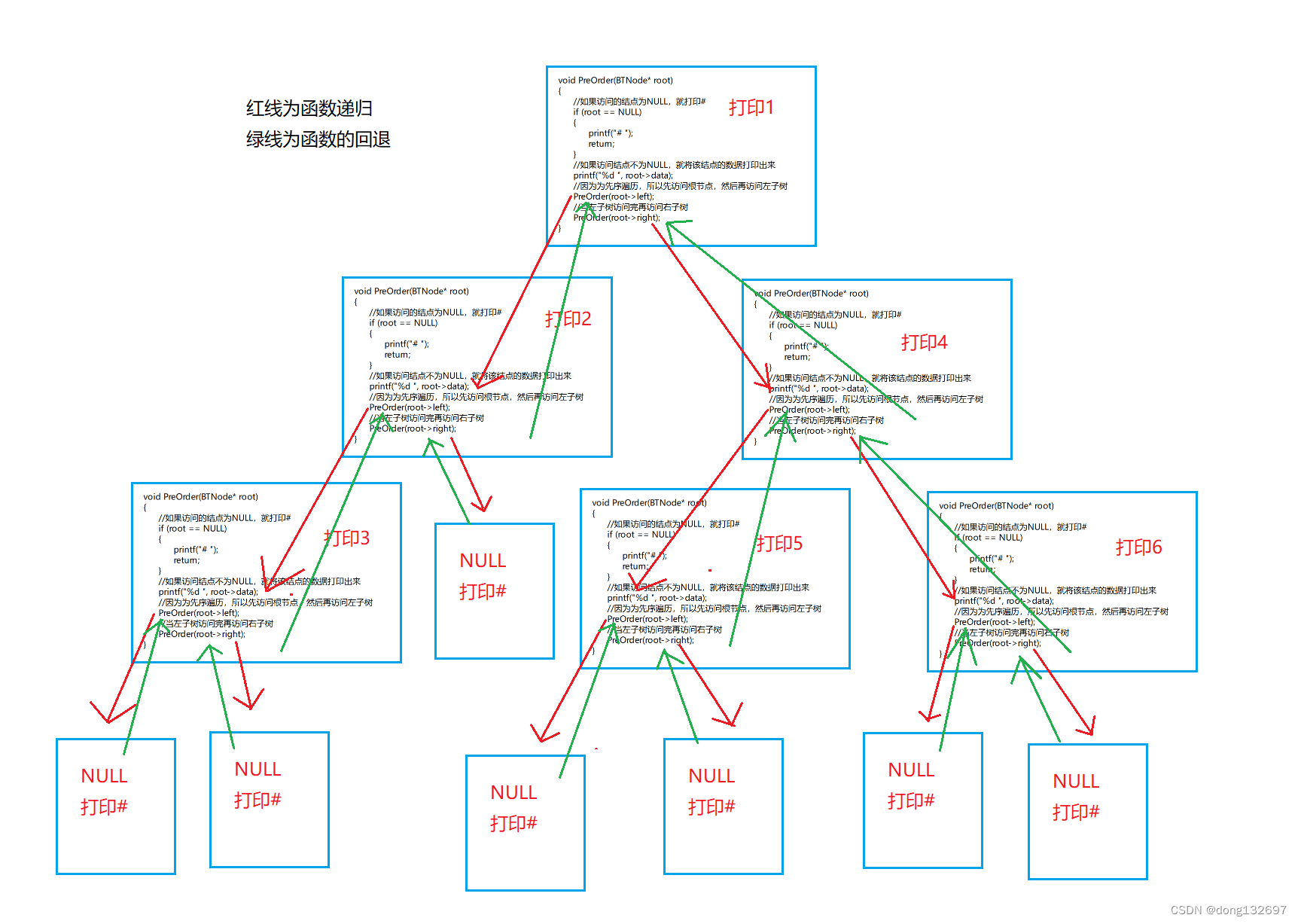
实现中序遍历

//中序遍历
void PreOrder(BTNode* root)
{
	//如果访问的结点为NULL，就打印#
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	//因为为中序遍历，所以先访问左子树，然后再访问根节点
	PreOrder(root->left);
	//左子树访问完后再打印根结点数据
	printf("%d ", root->data);
	//当根结点访问完再访问右子树
	PreOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

实现后序遍历

//后序遍历
void PostOrder(BTNode* root)
{
	//如果访问的结点为NULL，就打印#
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	//因为为后序遍历，所以先访问左子树，然后再访问右子树
	PostOrder(root->left);
	//当左子树结点访问完毕后，访问右子树结点
	PostOrder(root->right);
	//当左右子树结点都访问完后，再访问根节点数据
	printf("%d ", root->data);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

二、二叉树的一些操作的实现

当我们实现了二叉树的遍历后，就可以再实现二叉树的其他一些操作

1、求二叉树的结点个数

当要求二叉树结点时，我们想到的第一个方法就是定义一个全局变量count，然后再依次访问二叉树的结点，如果结点不为空，则count++，最后count的值就是二叉树中的结点个数。需要注意的是，当我们第二次调用这个方法时，因为count为全局变量，此时已经不为0，所以要重置count的值为0。

int count = 0;
void BinaryTreeSize(BTNode* root)
{
	//如果访问的结点为NULL，则count不进行+1
	if (root == NULL)
	{
		return;
	}
	//每访问到一个不为NULL结点就让count+1
	++count;
	//然后再去访问该结点的左子树和右子树
	BinaryTreeSize(root->left);
	BinaryTreeSize(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

上述方法使用全局变量得到树节点的数量是不安全的，并且全局变量可以被修改，而且每次调用函数时，还需要重置全局变量。所以我们可以使用第二种方法来求出二叉树结点个数。

int TreeSize2(BTNode* root)
{
	//当root结点为NULL时，就返回0
	if (root == NULL)
	{
		return 0;
	}
	//当root结点不为NULL，就返回root结点的数量，然后加上root结点左子树和右子树的结点的数量。
	return 1 + TreeSize2(root->left) + TreeSize2(root->right);
}
1
2
3
4
5
6
7
8
9
10

函数的递归和回退图。

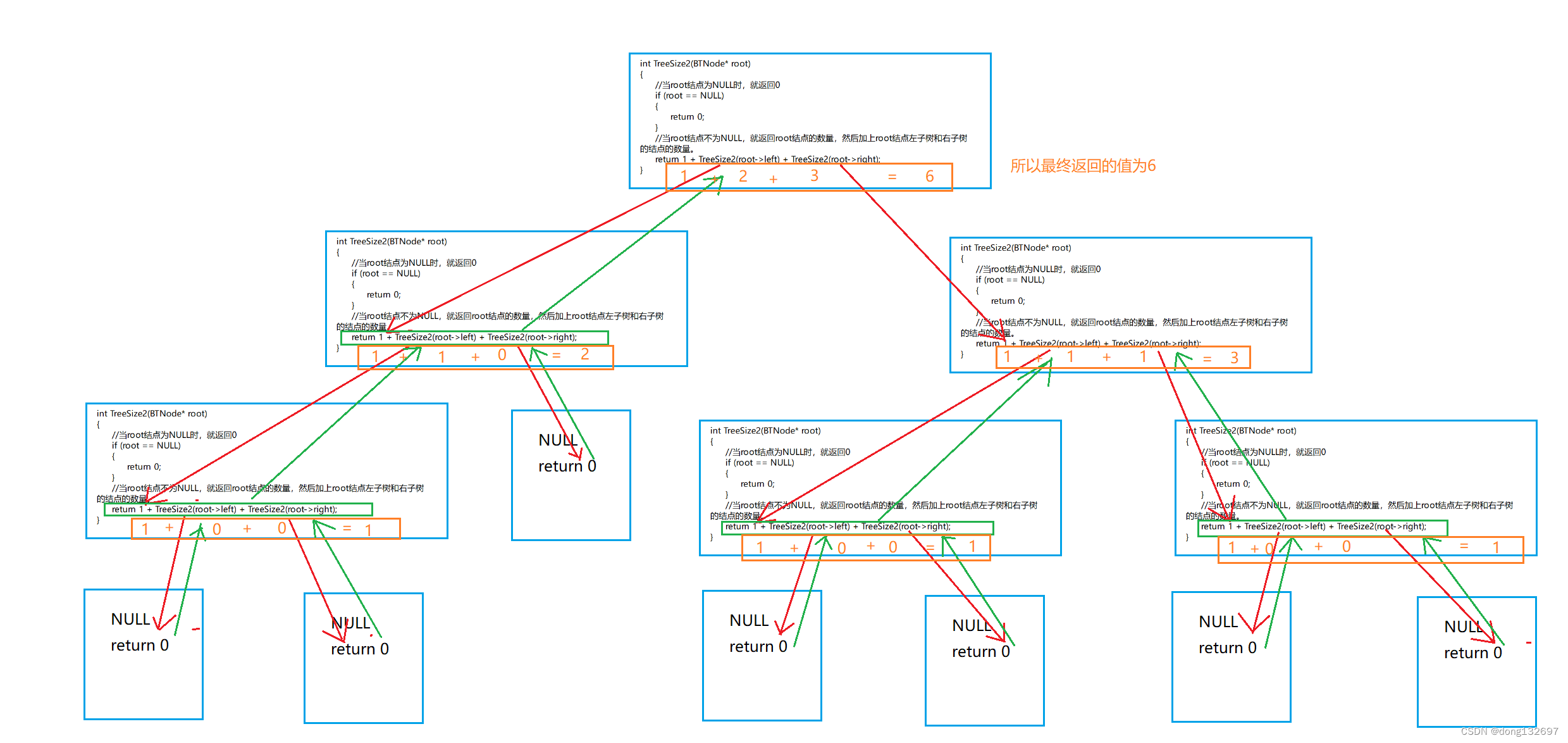
2、求二叉树叶子结点个数

//二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{
	//如果该结点为NULL，则返回0
	if (root == NULL)
	{
		return 0;
	}
	//如果该结点为叶子结点，则返回1
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	//如果该结点不为NULL，也不为叶子结点，就返回该节点的左子树和右子树中的叶子结点数
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

3、求二叉树第k层结点个数

//二叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k >= 1);
	//如果该结点为NULL，就返回0
	if (root == NULL)
	{
		return 0;
	}
	//k==1，说明要求的就是这一层的结点数，返回1
	if (k == 1)
	{
		return 1;
	}
	//如果该结点不为NULL，且k!=1，说明求的不是该层的结点数，让k-1，然后求该结点的左子树和右子树
	return BinaryTreeLevelKSize(root->left,k-1) + BinaryTreeLevelKSize(root->right,k-1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

4、求二叉树深度

//求二叉树深度
int BinaryTreeDepth(BTNode* root)
{
	//如果该结点为NULL，则深度为0
	if (root == NULL)
	{
		return 0;
	}
	//然后求出该结点的左子树和右子树的深度
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);
	//如果该结点的左子树深度大于右子树深度
	if (leftDepth > rightDepth)
	{
		//就返回该结点左子树的深度加这一层的深度
		return leftDepth + 1;
	}
	//如果该结点的左子树深度小于等于右子树深度
	else
	{
		//就返回右子树的深度加这一层的深度
		return rightDepth + 1;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

5、二叉树中查找值为x的结点

//二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	//当结点为NULL时，返回NULL
	if (root == NULL)
	{
		return NULL;
	}
	//当该结点数据为x时，返回该结点
	if (root->data == x)
	{
		return root;
	}
	//当该结点数据不为x时，先遍历该结点的左子树
	BTNode* left = BinaryTreeFind(root->left, x);
	//如果该结点的左子树返回的结点不为NULL，则说明在左子树中找到了存储x的结点，则此时left就存储该结点的地址。直接将left返回即可
	if (left!=NULL)
	{
		return left;
	}

	//如果该结点的左子树也没有查到就去遍历该结点的右子树，
	BTNode* right = BinaryTreeFind(root->right, x);
	//当该结点的右子树返回的结点不为NULL，则说明在右子树中找到了存储x的结点，此时right就存储该结点的地址。直接将right返回即可
	if (right!=NULL)
	{
		return right;
	}
	
	//当该结点的数据和该结点的左子树和右子树的结点中都没有该数据，则二叉树中没有该数据，此时返回NULL
	return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

6、二叉树的销毁

二叉树的销毁就是依次将二叉树的各结点申请的空间都释放，则需要遍历一遍二叉树，这里我们需要采用后序遍历，即先将根结点的左子树的结点释放完，再释放根结点的右子树的结点，最后再释放根结点的空间。因为如果采用先序遍历先将根结点空间释放，则就找不到根节点的左子树和右子树了。

//二叉树的销毁
void BinaryTreeDestroy(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	//采用后序遍历释放二叉树结点
	BinaryTreeDestroy(root->left);
	BinaryTreeDestroy(root->right);
	free(root);
}
1
2
3
4
5
6
7
8
9
10
11
12

三、二叉树层序遍历的实现

1、层序遍历

二叉树的层序遍历的实现需要队列的辅助。例如有下面一棵二叉树，先将二叉树的根结点入队列。

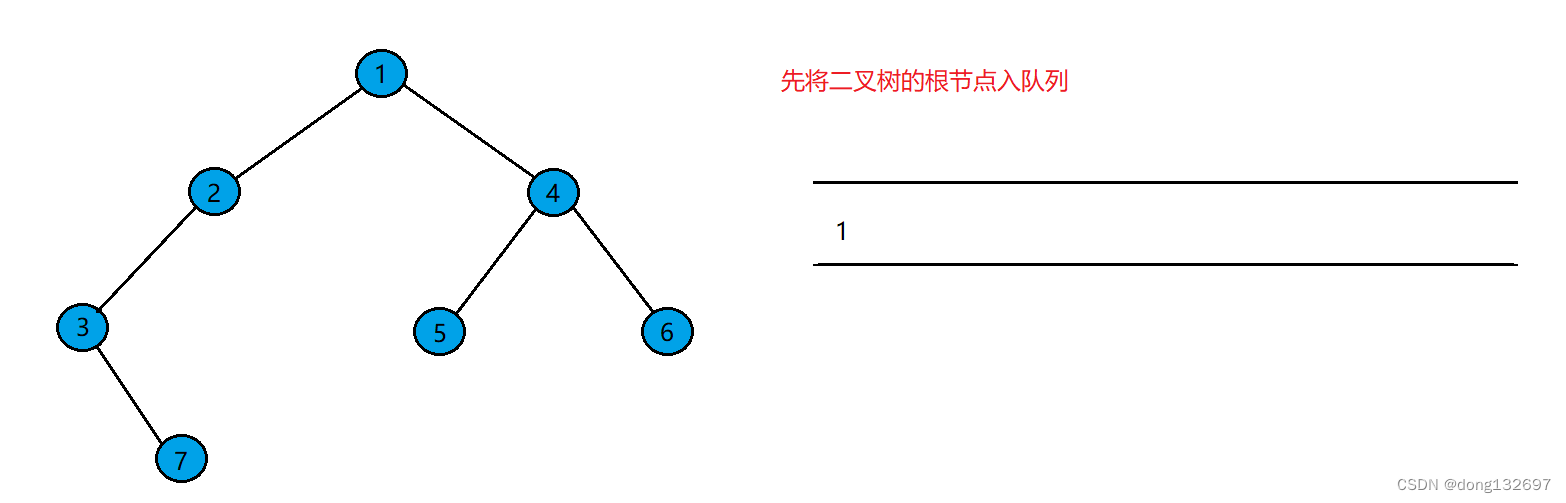
然后将队列的队头出队，并且将队头结点的左右孩子入队列。

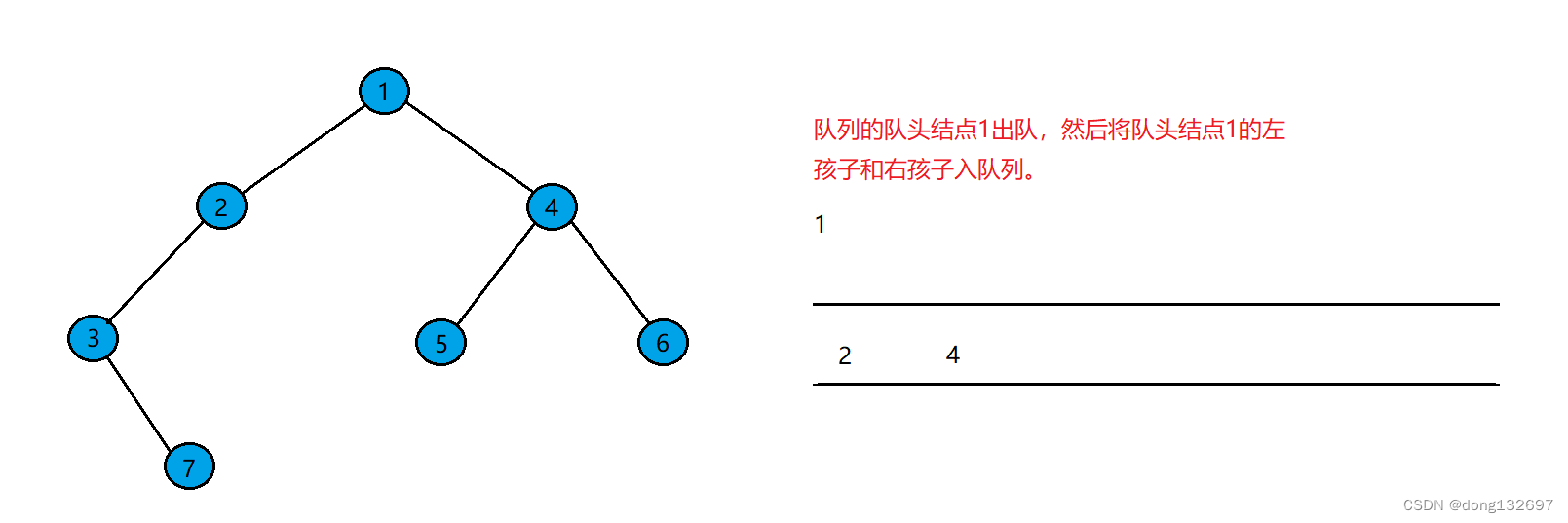
然后重复上述操作。将剩下的结点依次进入队列。

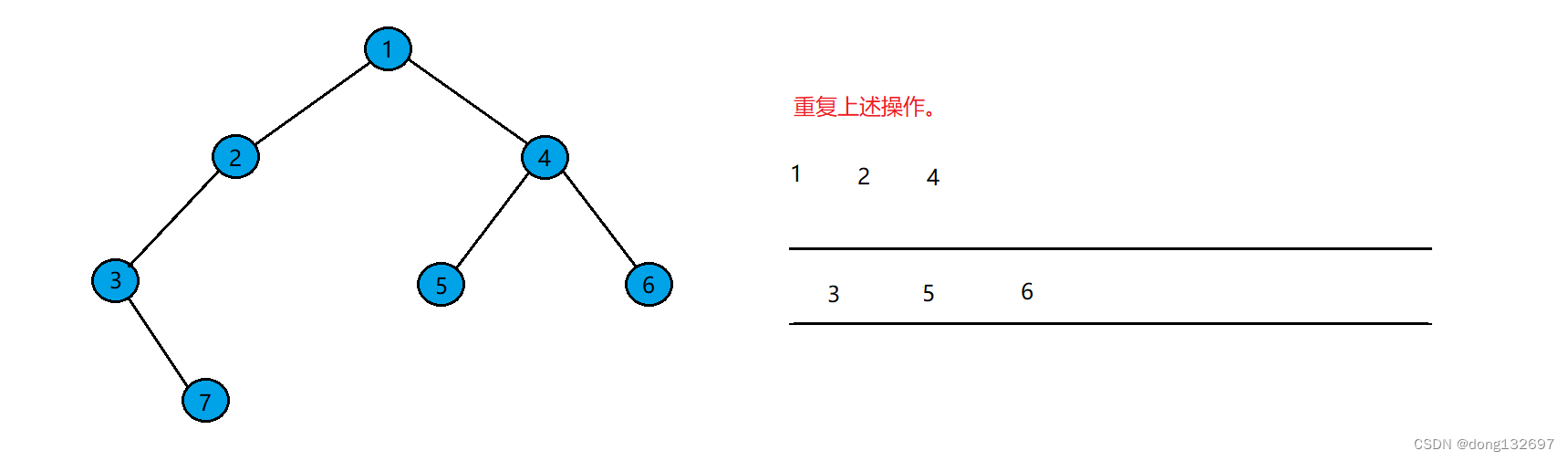
直到队列为空。结点出队的顺序即为二叉树层序遍历顺序。

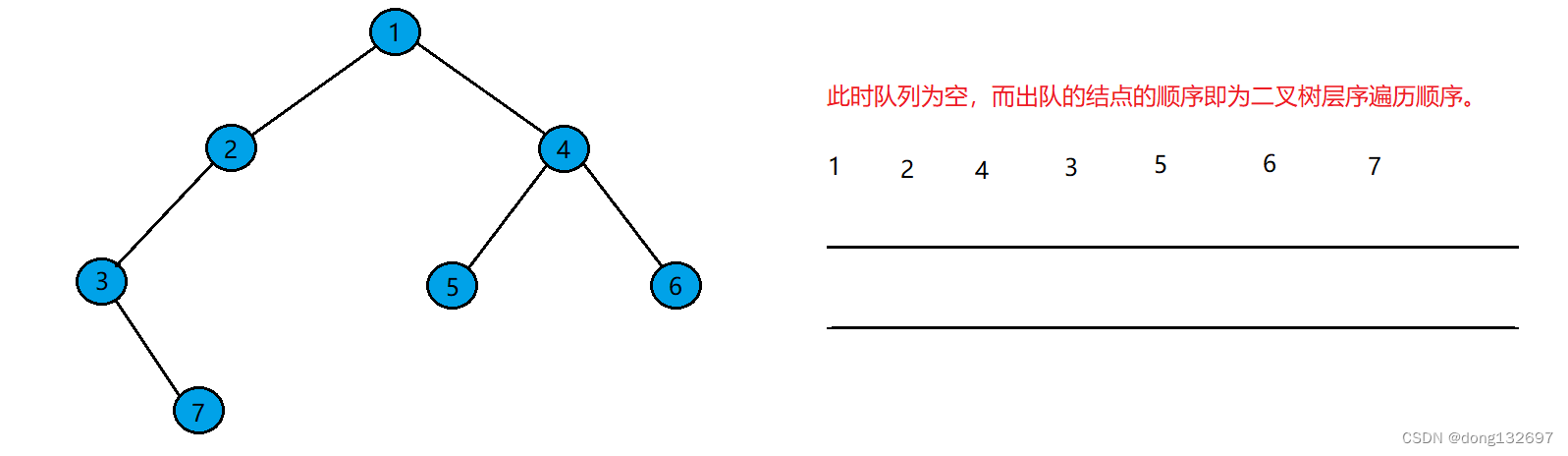
2、层序遍历代码实现

层序遍历需要借助一个辅助队列，先将二叉树根结点入队，然后让根节点出队，让根节点的左右孩子入队，然后让左右孩子出队，让左右孩子的左右孩子入队，依次循环下去，直到队列为空。

//二叉树的层序遍历
void LevelOrder(BTNode* root)
{
	//创建一个辅助队列
	Queue qt;
	QueueInit(&qt);
	//如果二叉树为空，就退出函数
	if (root == NULL)
	{
		return;
	}
	//将根节点的地址入队
	QueuePush(&qt, root);
	//如果队列中不为空，就进入循环
	while (!QueueEmpty(&qt))
	{
		//创建一个BTNode*类型的指针接收队列中队头结点存的地址
		BTNode* head = QueueFront(&qt);
		//将队头结点出队。
		QueuePop(&qt);
		//打印出队结点的数据
		printf("%d ", head->data);
		//如果出队结点的左孩子不为空，就将结点左孩子入队
		if (head->left != NULL)
		{
			QueuePush(&qt, head->left);
		}
		//如果出队结点的右孩子不为空，就将结点右孩子入队
		if (head->right != NULL)
		{
			QueuePush(&qt, head->right);
		}
	}
	printf("\n");
	QueueDestroy(&qt);

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

3、层序遍历应用 – 判断二叉树是否是完全二叉树

当有一棵二叉树需要判断其是否为完全二叉树时，此时就可以借用二叉树的层序遍历。
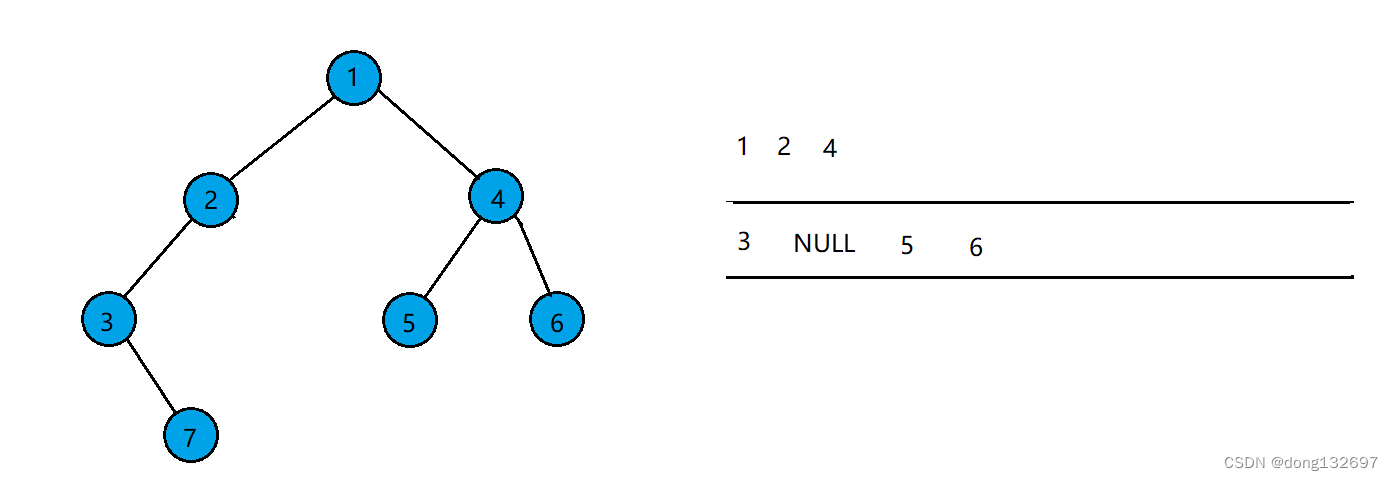
例如有如下一个完全二叉树，

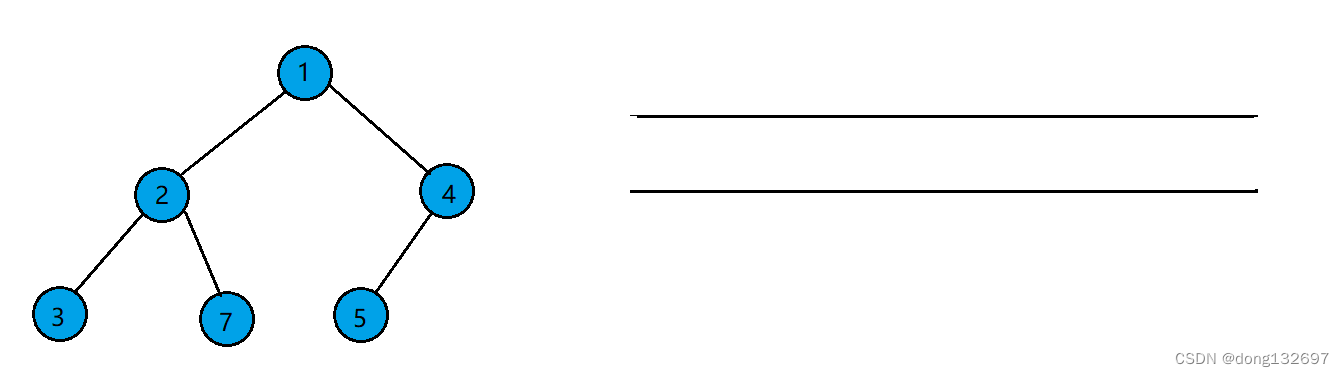
该二叉树按照层序遍历的步骤，先让根结点入队，然后队头结点出队，并让队头结点存的结点的左右孩子入队。如果左右孩子为空也入队。

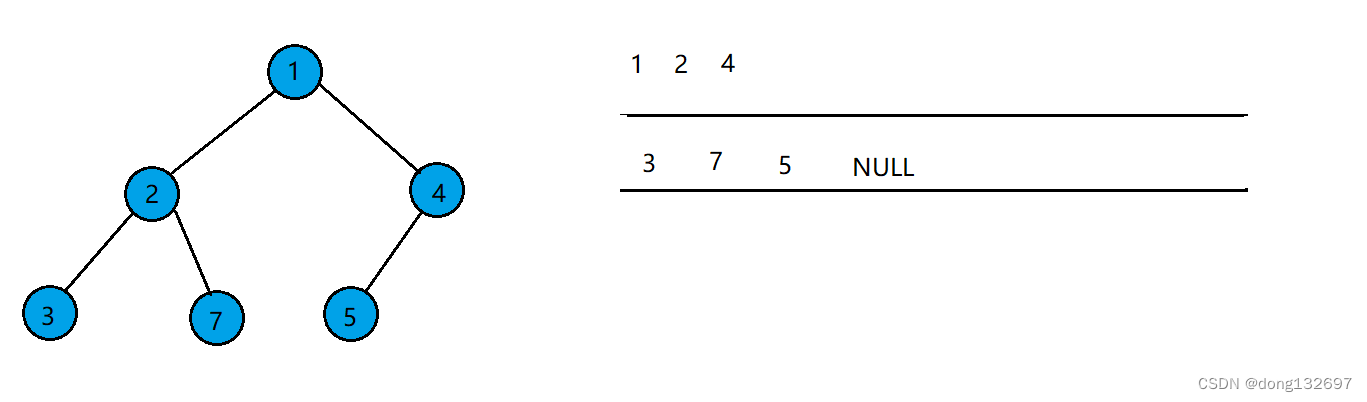
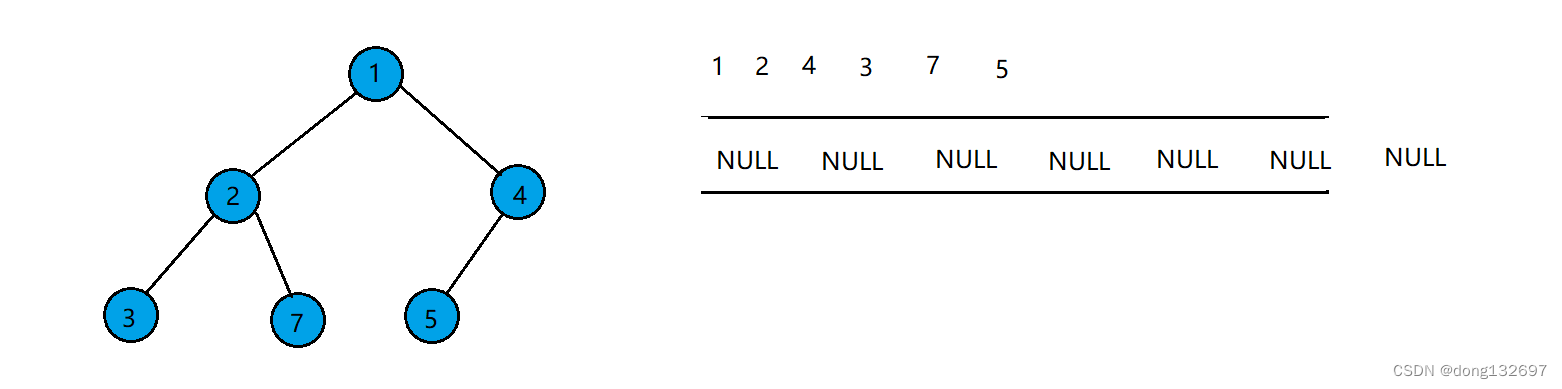
当队列中队头结点存的数据为NULL时，停止上述操作。此时队列中结点存储的数据全为NULL，可由此得出该二叉树为完全二叉树

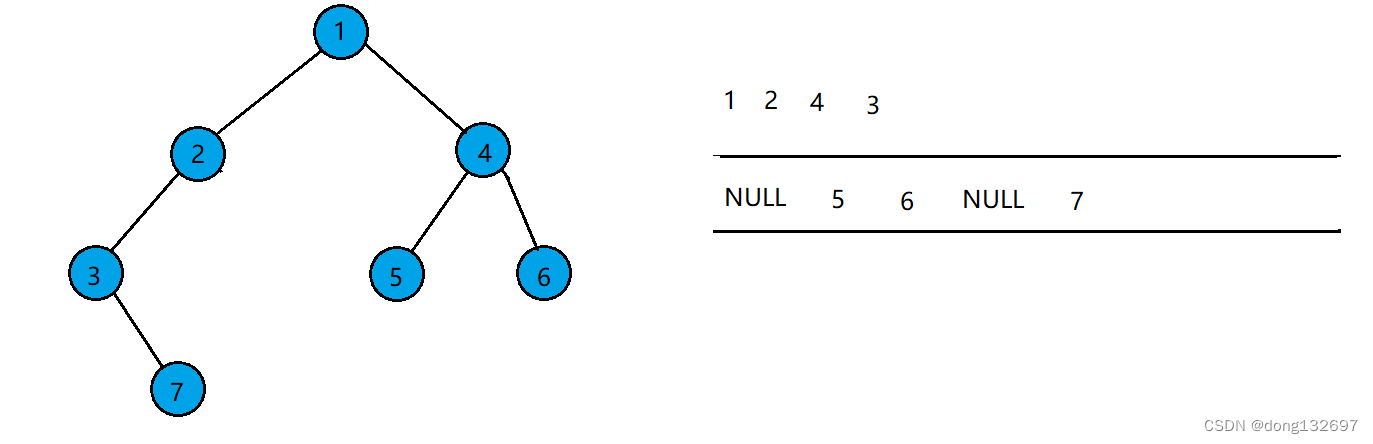
例如有如下一个非完全二叉树，

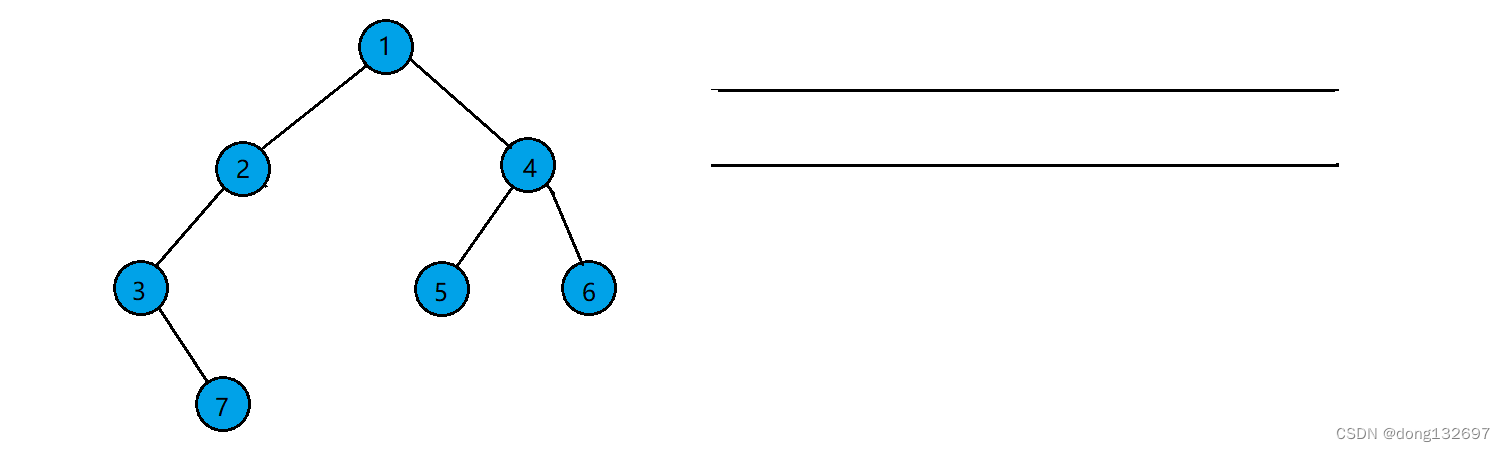
该二叉树按照层序遍历的步骤，先让根结点入队，然后队头结点出队，并让队头结点存的结点的左右孩子入队。如果左右孩子为空也入队。

当队列中队头结点存的数据为NULL时，停止上述操作。此时队列中的结点存储的数据有的为NULL，有的不为NULL，则可以由此得出该二叉树不为完全二叉树。

由上述的条件我们可以修改层序遍历的一些逻辑，使其可以判断二叉树是否为完全二叉树。

int BinaryTreeComplete(BTNode* root)
{
	//创建一个辅助队列
	Queue qt;
	QueueInit(&qt);
	
	//如果二叉树根节点不为空，就将根节点的地址入队列
	if (root != NULL)
	{
		QueuePush(&qt, root);
	}
	
	//如果队列中不为空，就进入循环
	while (!QueueEmpty(&qt))
	{
		//将队列的队头结点存的数据返回
		BTNode* head = QueueFront(&qt);
		//将队头结点出队
		QueuePop(&qt);
		//如果该队头结点存的数据不为NULL，就将该结点的左右孩子入队,左右孩子为NULL也入队
		if (head != NULL)
		{
			QueuePush(&qt, head->left);
			QueuePush(&qt, head->right);
		}
		//如果该队头结点存的数据为空，说明已经到达队列中第一个NULL，此时跳出循环
		else
		{
			break;
		}
	}
	//此时如果队列不为空，就继续遍历队列中的元素
	while (!QueueEmpty(&qt))
	{
		//将队头结点存的数据返回
		BTNode* head = QueueFront(&qt);
		//将队头结点出队
		QueuePop(&qt);
		//如果队列中第一个NULL后还有队列结点存的数据不为NULL，则说明该二叉树不为完全二叉树
		if (head != NULL)
		{
			//将队列销毁
			QueueDestroy(&qt);
			//返回0则代表该二叉树不是完全二叉树
			return 0;
		}
	}
	//如果当队列中结点全部遍历完，并且存的数据都为NULL，说明该二叉树为完全二叉树
	//销毁队列
	QueueDestroy(&qt);
	//返回1代表为完全二叉树
	return 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53