vmd变分模态分解程序matlab论坛_希尔伯特谱、边际谱、包络谱、瞬时频率/幅值/相位——Hilbert分析衍生方法及MATLAB实现...

上一篇文章对希尔伯特-黄变换（HHT）的前世今生进行了介绍。

不过在研究中通常并不是到希尔伯特-黄变换就停止了。

而是要用到诸如希尔伯特谱、包络谱、边际谱、瞬时频率/幅值/相位等方法进一步分析。

这些方法究竟是什么含义，以及怎样使用、怎样实现呢？

一、希尔伯特谱（Hilbert Spectrum）

希尔伯特谱是希尔伯特-黄变换得到的最直观结果，（上一篇文章中倒数第二张图——经过HHT的“疯狂的M”），其反映的是信号时间、瞬时频率和幅值之间的关系。该图谱可以用于分析包含混合分量信号中各分量随时间变化的规律，以识别局部特征。需要注意的是，希尔伯特谱有时是将emd分解后所有imf分量作为分析对象的，而有些会有针对性地挑选出某个或某几个imf分量分析，具体怎样操作是要结合具体研究内容有针对性地选择的。

下边使用一个模拟的轴承故障信号，使用希尔伯特谱寻找缺陷[1]。

模拟在轴承外圈引入一个缺陷，该缺陷导致一系列冲击，导致磨损逐渐加剧。这些冲击将在轴承的外环故障频率(BPFO)处重复出现。

模拟出的轴承故障振动特征信号如下图：

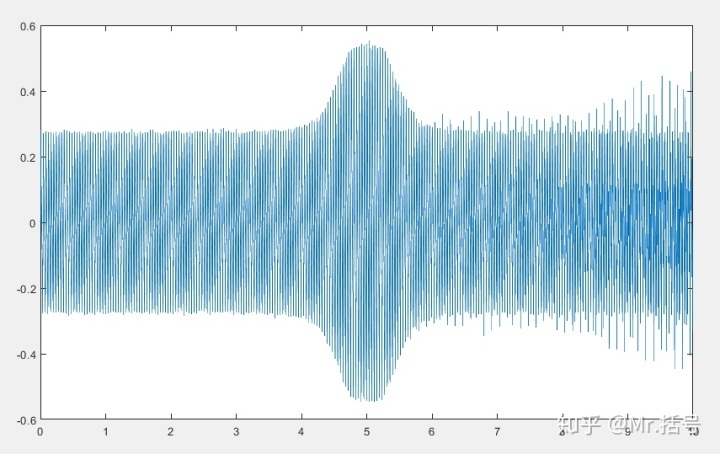
在4~6秒之间的尖峰是由于轴承振动激发的共振引起的[1]，而从5~10秒之间，信号中叠加了幅值逐渐增加的冲击信号。

对该信号进行EMD分解，其中的部分分量如下图。

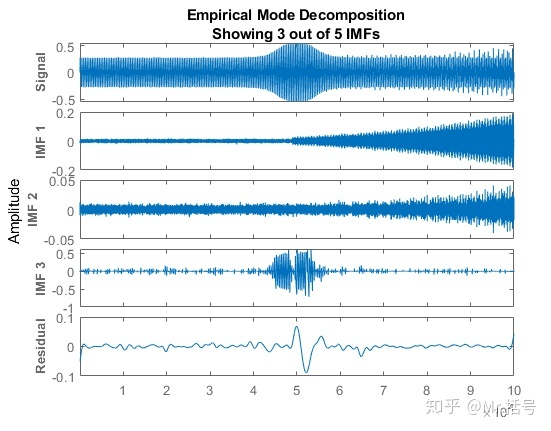
对IMF1做希尔伯特谱，得到下图结果。随着轴承磨损的逐渐加剧，冲击能量增加，在2500~3500Hz范围内希尔伯特谱幅值随之增大。

对IMF3做希尔伯特谱，得到下图结果。这里将轴承振动激发的共振信号分离出来，其频率范围在0~100Hz之内。