关于使用快慢指针解决环形链表问题_快慢指针解决链表环问题

关于使用快慢指针解决环形链表问题

作者：@ 不进大厂不改名
专栏：@ 数据结构
作者简介：大一学生 希望能学习其同学和大佬的经验！
本篇博客简介：有关快慢指针解决链表相关的问题

1.LeetCode 题目以及分析

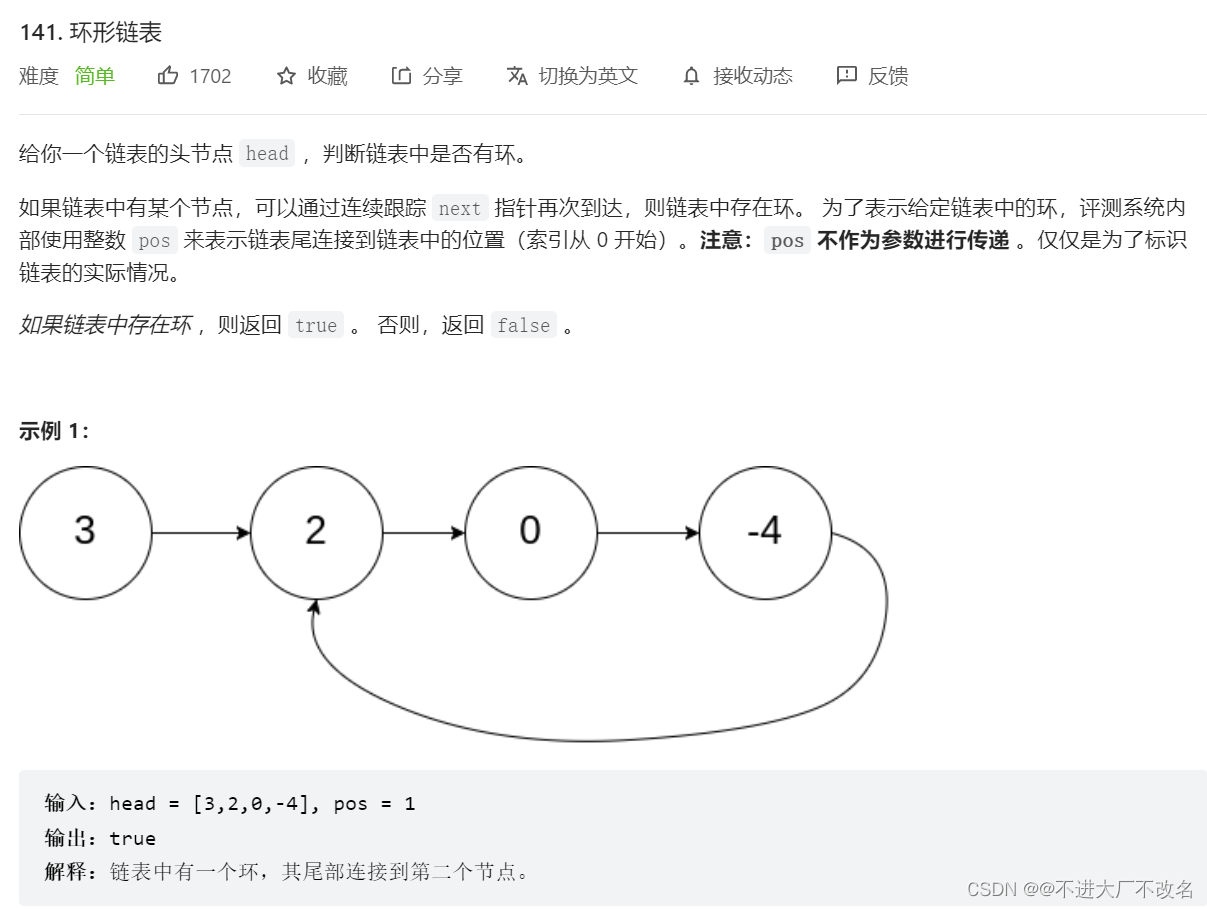
1.题目：# 关于使用快慢指针解决环形链表问题

1.LeetCode 题目以及分析

1.题目：

2.分析：判断一个链表是否带环，我们第一个能想到的是看元素是否重复，经过分析这个不行如果出现多个(两个或以上)相同元素这个方法就不行。因此我们引入新的方法：快慢指针。定义两个指针：快指针(fast)和慢指针(slow)。快指针一次走两步，慢指针一次走两步。

当慢指针走到一半长度，快指针进环

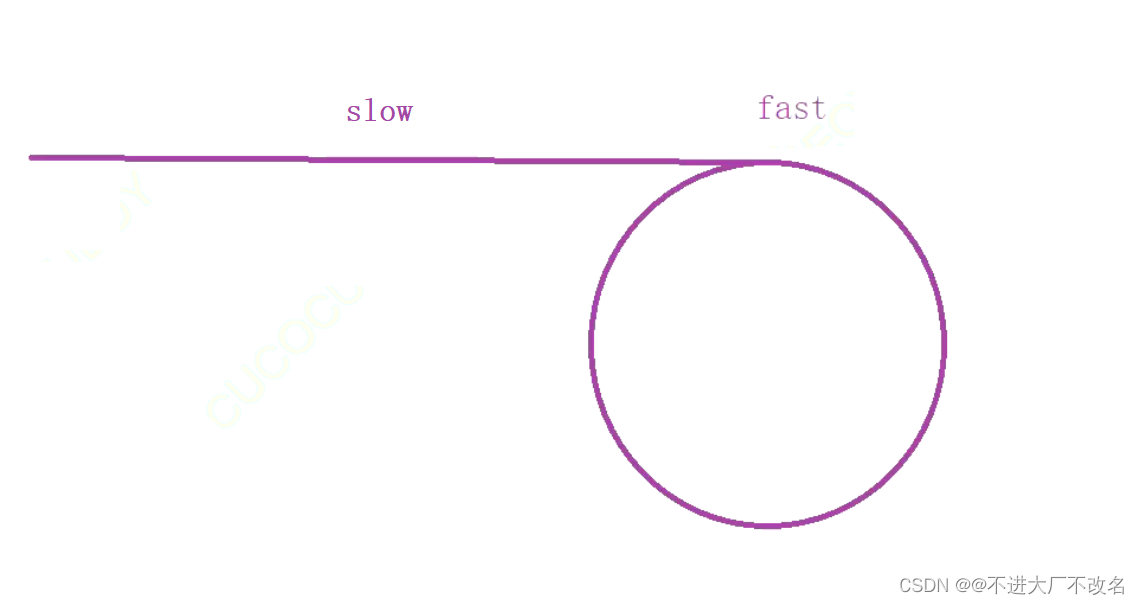
当慢指针进环，快指针开始追慢指针

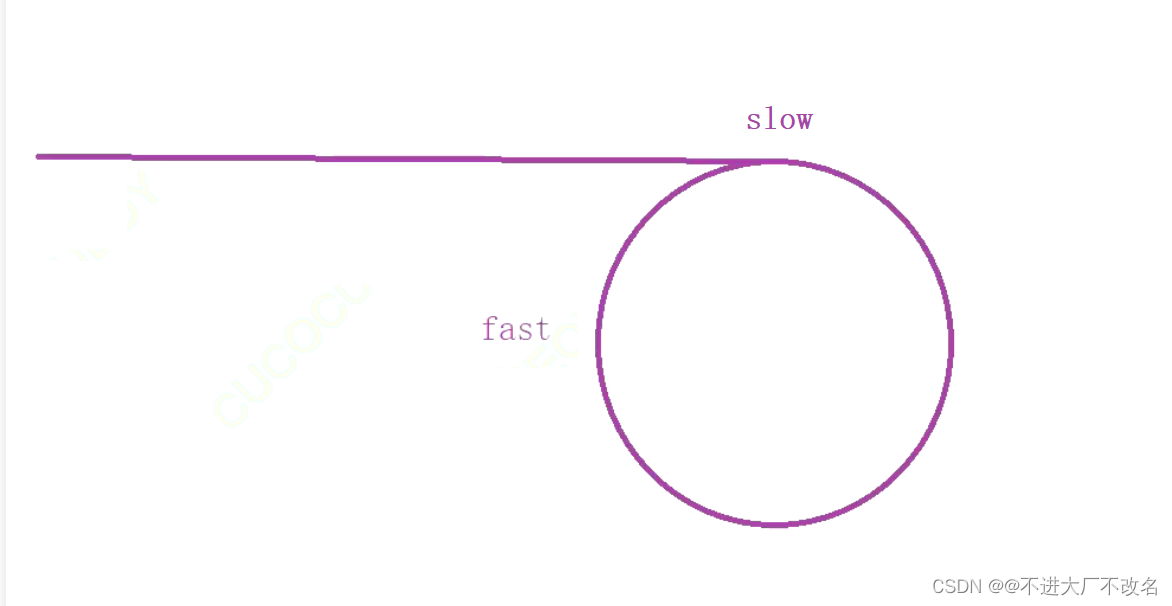
最后快指针追上慢指针

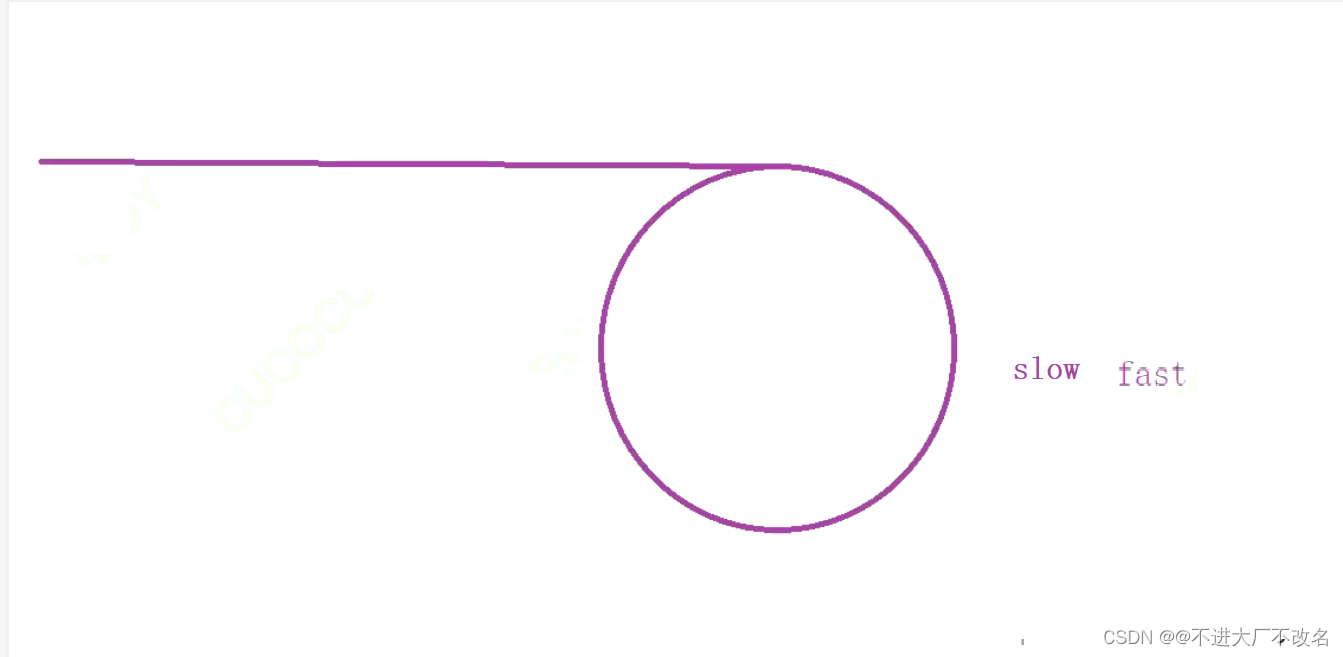
代码如下：

/**
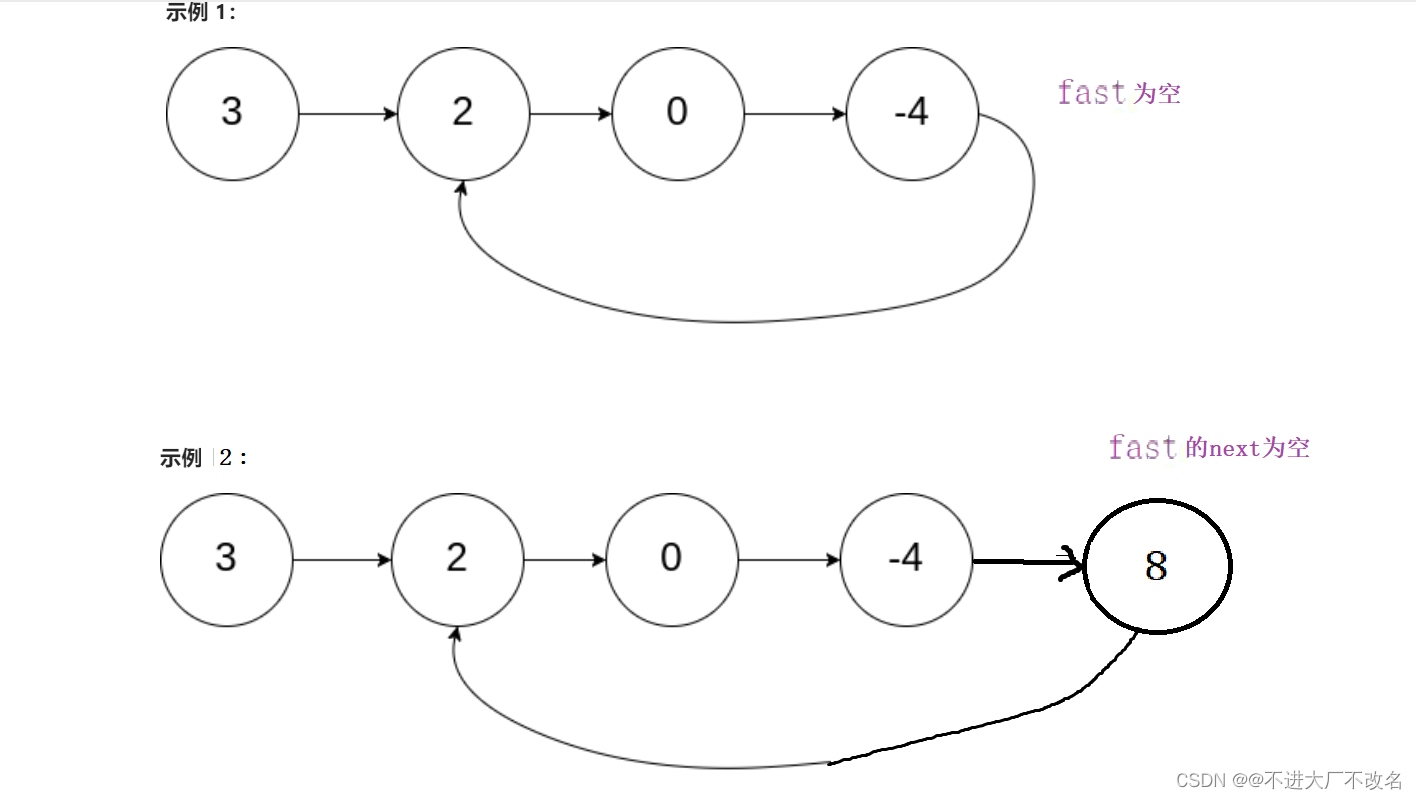
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head)
{
    struct ListNode*slow=head;
    struct ListNode*fast=head;
    while(fast!=NULL&&fast->next!=NULL)//循环条件：当个数是偶数个时，快指针不是空并且是奇数个时快指针的下一个不是空时继续，当其中一个为空时条件结束。
    {
        slow=slow->next;//慢指针走一步
        fast=fast->next->next;//快指针走两步
        if(fast==slow)
        {
            return true;
        }
    }
    return false;
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

提交成功的图片:

2.关于本题的深度分析(大厂最爱考)

1.问题：

1.结论和分析：(快指针一次走两步，慢指针一次走一步)
结论：一定能追上(相遇)
分析：假设慢指针进环后，快慢指针之间的距离时N，此时快指针一次走两步，慢指针一次走一步，它们之间的距离每走一次减少一。当距离为0时它们就相遇了。这种情况一定能相遇。
它们之间的距离变化：
N
N-1
N-2
N-3
······
2
1
0

2.结论和分析：(快指针一次走三步，慢指针一次走一步)
结论：不一定能追上(相遇)
分析：假设慢指针进环后，快慢指针之间的距离时N，此时快指针一次走三步，慢指针一次走一步，它们之间的距离每走一次减少二。
它们之间的距离变化：

N
N-2
N-4
N-6
······
4
2
0
如果N为偶数

N
N-2
N-4
N-6
······
5
3
1
-1
如果N为奇数

距离为-1时表示快指针已经超过慢指针，如果此时**环的长度©**减一(C-1)是奇数时就永远追不上，如果是偶数时可以追上

所以快指针一次走三步，慢指针一次走一步不一定能追上。

3.结论和分析：(快指针一次走四步，慢指针一次走一步)
结论：不一定能追上(相遇)
分析：同上