Pytorch线性回归

使用pytorch来重现线性模型的过程，构造神经网络module，构造损失函数loss，构造随机梯度下降的优化器sgd。

一 revise

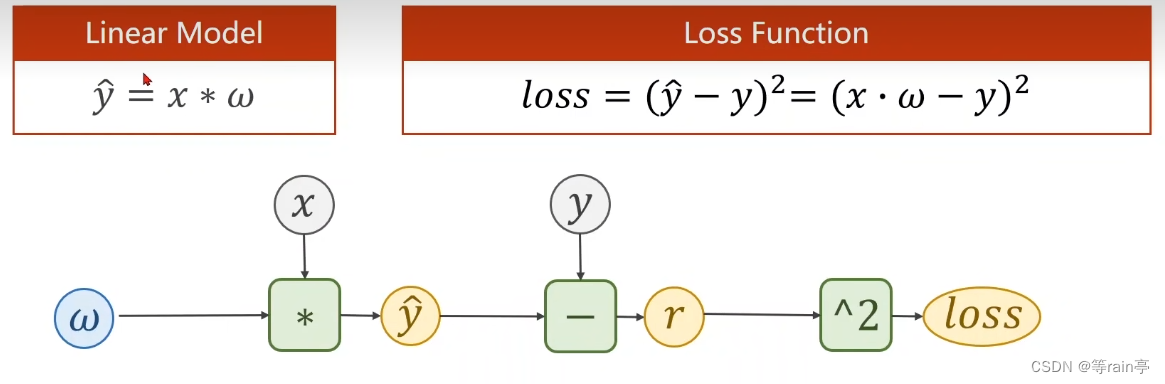
首先确定我们的模型，我们希望完成的目标就是得到较小的loss，所以我们就需要一个标量值的loss。

那其实在上一部分的内容就提到了tensor，loss，backward的使用，其实这个就是我们利用pytorch给我们的功能了。

二 pytorch fashion

pytorch写神经网络的第一步就是要准备数据集（有构造数据集的工具），设计一个模型计算y_head，构造损失函数和优化器，写训练的周期（前馈反馈更新）。

2.1准备数据

我们之前准备数据，就是直接使用列表。

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

In pytorch , the computational graph is in mini-batch fashion，so X and Y are 3x1 Tensor.

但是现在我们希望它不在是一个列表或者一个向量，我们希望它可以成为一个3X1的矩阵。当然公式依然还是使用之前的y_head = w*x +b 。图中的y_pred 就是我们说的y_head。

大家可能注意到我们上面说计算图使用小批量的方式（mini batch），这其实就是把x的三个数据同时放在一起，同时进行计算。

现在我们有了3x1矩阵的x了，那我们就可以得到3x1矩阵的y。因为存在广播机制，看图中w和b，其实也会变成3x1的矩阵。

当然loss函数的公式也是和之前不变为（y_head - y）**2。此时loss和y也会变成3x1的矩阵。

说了这么多，无非就是要把数据处理成矩阵的形式那使用tensor的方式就是：

import torch
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[2.0],[4.0],[6.0]])

总结来说，使用mini batch构造数据集的时候，我们就是需要x和y都是矩阵的形式。

2.2 构造计算图

最开始计算梯度手工计算，后来我们构建计算图可以自动把梯度求出来，之后就可以进行优化了。  

因此我们在准备好数据的基础上，下一步就是构造出计算图。我还是使用y_head = x*w + b这样一个函数（放仿射模型）。我们通过这个构建出计算图的一部分叫线性单元。

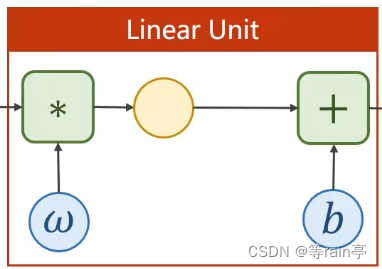
那其实我们现在进行计算的都是矩阵，既然计算矩阵就需要确定w的大小和b的大小。就需要从z和x的维度来确定w和b的维度。

接下来我们需要把y_head放到loss函数中进行计算，上面我们也说到，loss必须是一个标量（只有是标量的情况下才可以backward）。现在y_head是一个矩阵形式，且y也是，得到的loss应该也是矩阵形式，此时我们就需要对loss进行适当的修改，通常会对loss内的数进行求和，使其变成一个标量。

class LinearModel(torch.nn.Module):
    def __init__(self): #初始化
        super(LinearModel,self).__init__()
        self.linear = torch.nn.Linear(1,1)
    
    def forward(self,x): #前馈
        y_pred = self.linear(x)
        return y_pred
 
model = LinearModel()

大家可以看见，我们在类中没有写反馈的函数，这是由于model构造出的对象会自动根据计算图去实现backward。

（1）构造函数的super不用变。

torch.nn.Linear 使pytorch中的一个类，这个类里面的对象包括了权重w和偏置b，就可以直接完成下面的整个运算。Linear也是源于Model，所以他也可以进行自动的反向传播。

class torch.nn.linea(in_features,out_features,bias=True) 所做的计算就是y=ax+b。其中in_features表示的就是输入的x是几维的，out_features表示的就是输出的是几维的。那我们在mini batch中矩阵的行表示的使各个样本的值，那此时不难猜出矩阵的列表示的就是feature。bias为True表示需要偏置量，默认为True。

、

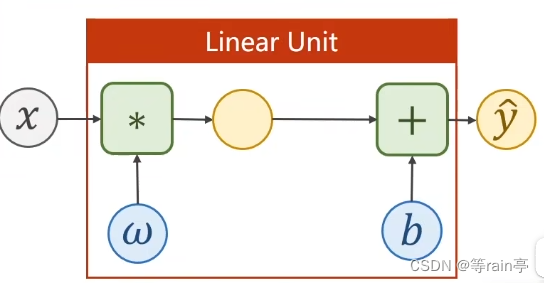下面两个计算公式都可以，注意w在矩阵乘法的位置。

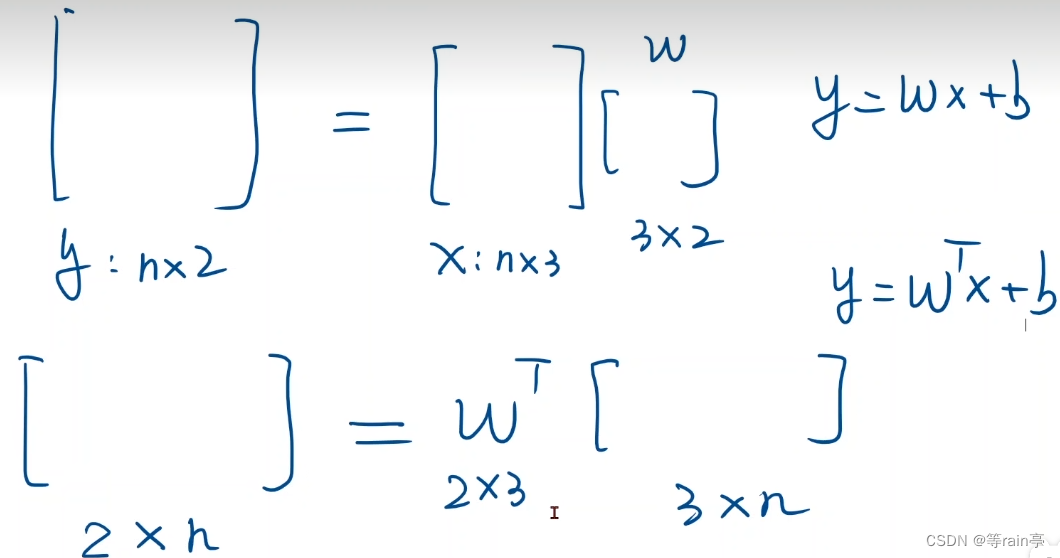
（2）forward(self,x)

 y_pred = self.linear(x) 这一步其实就是在计算我们的y_head。其实看上面的定义也可以看出来。

（3）最后将模型进行实例化，供我们后面使用。

2.3构造损失函数和优化器

（1）损失函数

我们还是使用MSE损失函数，此时也还是需要构建计算图，整体过程就是在拿到y_head的前提下，对y进行计算，得到loss的值，此时loss还是一个矩阵的形式，最后还需要对其进行变成标量。

class torch.nn.MSELoss(size_average=True,reduce=True) 

其中size_average是是否求均值。reduce是是否进行降维，也就是是否进行求和。

现在这个size_average被废除了，大家可以看下列代码实现求均值的True or False。

#criterion = torch.nn.MSELoss(size_average=True)
#改为：
criterion = torch.nn.MSELoss(reduction='mean')
 
#criterion = torch.nn.MSELoss(size_average=False)
#改为：
criterion = torch.nn.BCELoss(reduction='sum')

因此对于criterion这个对象需要的参数是（y_head，y）

（2）优化器

optimizer = torch.optim.SGD(model.parameters(),lr=0.01)

优化器是不会建立计算图的。

model.parameters() 这个指的是权重。简单来说就是model中其实没有定义权重，model里存在我们上面定义的成员linear，linear中包含两个权重w和b。现在就需要告诉优化器哪些tensor是需要优化的，哪些是用于梯度下降的。因此在使用SGD这个模型时，想找权重，直接model.parameters。可以把model中所有的参数全部找到。

lr时学习率，一般会给一个固定的值。可以在不同的部分使用不同的学习率。

2.4训练过程

for epoch in range(100):
    y_pred = model(x_data)  #先计算出y_head
    loss = criterion(y_pred,y_data) #再计算出loss
    print(epoch,loss.item()) 
    
    optimizer.zero_grad()#在反馈前将梯度清0
    loss.backward()#反馈
    optimizer.step()#更新

整个过程其实就先算y_head，再计算loss，随后backward，更新。

最后就是打印一下权重信息。

# w b
print('w=',model.linear.weight.item())
print('b=',model.linear.weight.item())
 
#Test Model
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred=',y_test.data)

对于我们给出的x_data和y_data，其实最终最好的情况是w=2 b=0。

分别是100次epoch和1000次epoch的结果，看得出来1000次更接近于我们想要的值。