线性代数基础【6】二次型_用python求所有正定矩阵p,使得ptap=b

第一节、二次型的基本概念及其标准型

一、基本概念

①二次型

含n个变量x1,x2,…,xn,且每项都是2次的齐次多项式

②标准二次型

只含有平方项不含交叉项的二次型称为标准二次型

③二次型的标准化

设f(X)=X^TAX 为一个二次型,经过可逆的线性变换X=PY(即P为可逆矩阵)把二次型f(X)=X^TAX化为

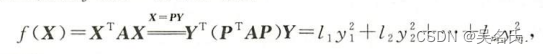
这个过程称为二次型的标准化

注意:

(1)任何一个二次型f(x1,x2,…,xn)都可以表示为矩阵形式,且A^T = A,其中X^TAX 为标准二次型的充分必要条件是A为对角阵;X^TAX是非标准二次型的充分必要条件是A是对称而非对角的矩阵

(2)二次型X^TAX标准化的过程即实对称矩阵A对角化的过程,二次型标准化过程必须遵循两点原则:

①线性变换X=PY中的矩阵P一定为可逆矩阵

②P^TAP为对角矩阵

(4)(惯性定理)二次型的标准形不唯一,但标准形中正、负系数的个数是唯一确定的

④规划二次型

系数为1和-1的标准形,称为二次型的规范形

⑤可逆的坐标变换

⑥矩阵合同

设A,B为n阶实对称矩阵,若存在可逆矩阵P,使得P^TAP=B,称矩阵A与B合同,记为A≌B.

注意:

(1)经过可逆线性变换的二次型的矩阵与原矩阵之间合同

(2)矩阵合同关系具有:

①A≌A(反身性)

②若A≌B,则B≌A(对称性)

③若A≌B,B≌C,则A≌C(传递性)

(3)要正确区分矩阵的三大关系:即等价关系、相似关系、合同关系

①矩阵等价

设A,B为同型矩阵(不一定为方阵),若A经过有限次初等变换化为B,称A与B等价

判别法:

方法一:设A,B为同型矩阵,则A,B等价的充分必要条件是r(A)=r(B)

方法二:设A,B为同型矩阵,则A,B等价的充分必要条件是存在可逆矩阵P,Q,使得PAQ=B

②矩阵相似

设A,B为n阶矩阵,若存在可逆矩阵P,使得P^-1AP=B,称A与B相似,记为A~B

判别法:

设A,B为n阶矩阵,若A,B的特征值相同且A,B都可相似对角化,则A~B

③矩阵合同

设A,B为n阶实对称矩阵,若存在可逆矩阵P,使得P^TAP=B,称A与B合同,记为A≌B

判别法:设A,B为实对称矩阵,则A≌B的充分必要条件是A,B的正、负、零特征值个数相同

二、基本定理

三、二次型标准化方法

①配方法

即通过配方的方法把二次型化为若干部分的平方和与差,然后进行变换的方法

②正交交换法

即可逆线性变换X=QY中,Q是正交矩阵,且经过变换X=QY可把二次型化为标准形的变换

第二节、正定矩阵与正定二次型

一、基本概念

(1)例子

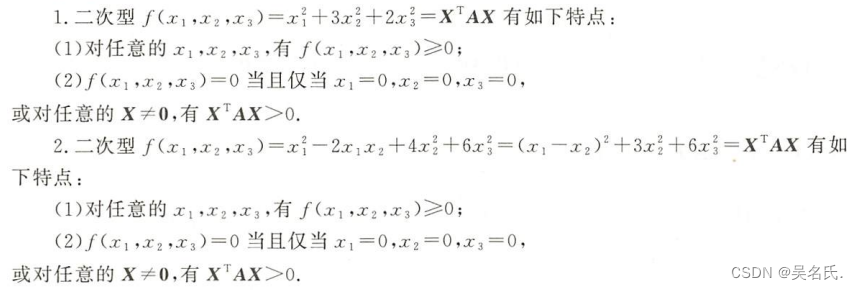
(2)正定二次型概念

对二次型f(x1,x2,…,xn)=X^TAX,若对任意的X≠0,总有 X^TAX>0,称 X^TAX为正定二次型，A称为正定矩阵

一、正定二次型的判别

定理1 二次型X^TAX为正定二次型的充分必要条件是A的特征值全为正数

定理2 二次型X^TAX 为正定二次型的充分必要条件是A的顺序主子式都大于零,即

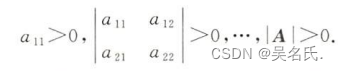
定理3 设A^T=A, 则A为正定矩阵的充分必要条件是存在可逆矩阵B,使得A=B^TB

定理4 设A^T=A,则A为正定矩阵的充分必要条件是A与E合同.

定理5 设A^T=A,则A正定的充分必要条件是A的正性指数为n

注意:

(1)二次型f(X)=X^TAX 正定的必要条件是:aij>0(i=1,2,…,n);|A|>0

(2)若A是正定矩阵,则A一定是可逆矩阵

(3)若A是正定矩阵,则A^-1 及 A^*是正定矩阵

(4)若A,B都是正定矩阵,则 A+B 是正定矩阵