热门标签
热门文章
- 1Java——Java快速入门_java入门
- 2pycharm配置conda环境时显示找不到conda.exe文件+解决pycharm非零退出代码Non-zero exit code(pip更新无效)
- 3NLP 自然语言处理实战
- 4「 运动控制 」“运动控制、过程控制、动态控制、运动规划、轨迹规划、路径规划”浅谈_动态运动基元是属于运动规划还是运动控制
- 5python常用代码总结-python字典的常用方法总结
- 6el-tree懒加载以及动态局部刷新数据,添加指示虚线_el-tree 动态样式
- 7移动Web系统中无监督KPI异常检测的监督式微调
- 8boot/loader.asm_asm booloader
- 9力扣每日一道系列 --- LeetCode 160. 相交链表
- 10从高考到程序员的成长之路_高考程序
当前位置: article > 正文
自己用java实现二叉树的增,删,查_java 二叉树增删改查
作者:菜鸟追梦旅行 | 2024-03-25 03:25:49
赞
踩
java 二叉树增删改查
在看TreeMap的源码之前,有必要先了解下tree这个数据结构,很早之前看java版的数据结构与算法,也是卡到tree这里,没再读下去。现在重新复习这块知识。先从二叉树开始吧,BST 英文 binary search tree 直译二分查找树。
![]()
某个节点的值都大于该节点的左子树里所有的节点。反之右子树的所有节点的值都大于该节点。
记忆 : 大佐(左)
节点 有父类节点,左子树节点,右子树节点,实现了Comparable的value
- static class Node implements Comparable{
- Node parent;//父类节点
- Node left;//左子树节点
- Node right;//右子树节点
- Comparable value;//实现了Comparable的value
- public Node(Node parent, Comparable value, Node left, Node right){
- this.parent=parent;
- this.left=left;
- this.right=right;
- this.value=value;
- }
- }
它的操作主要有
a.插入
b.遍历
假设如下
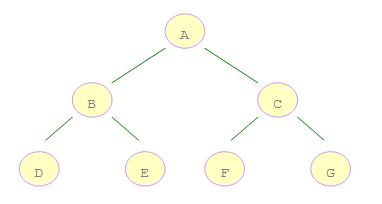
遍历又分为
1.深度优先:
沿着树的深度遍历树的节点,尽可能深的搜索树的分支,
深度优先遍历又分为前序遍历,中序遍历,后序遍历
上面二叉树的前序遍历
顺序为:ABDECFG
上面二叉树的中序遍历
顺序为:DBEAFCG
上面二叉树的后序遍历
顺序为:DEBFGCA
根节点在哪个位置输出就是什么顺序遍历
2.广度优先 :
从根结点开始沿着树的宽度搜索遍历,
上面二叉树的遍历顺序为:ABCDEFG
c.删除
1.删除的节点只有右子树,只要把节点的父节点的右子树指向删除节点的右子树
eg:删除52后, 50.right(52.parent)--->54(52.right)
2.删除的节点只有左子树,只要把节点的父节点的左子树指向删除节点的左子树
eg:删除83后,85.left(83.parent)--->54(83.left)
3.删除的节点有右子树和左子树。有2种算法
从删除的节点的左子树里找到最大的值,作为删除节点的父节点的左或右子树(依据于删除节点原来是父节点的左或右)
eg:删除35后,68.left(35.parent)--->33
从删除的节点的右子树里找到最小的值,作为删除节点的父节点的左或右子树(依据于删除节点原来是父节点的左或右)
eg:删除35后,68.left(35.parent)--->50,删掉50后,后续52接上
纸上得来终觉浅,绝知此事要躬行。接下来就是撸代码了,主要是理解原理的基础上来写就不会觉得很难。
1.定义一个类MyBST
里面有static class Node。是不是和hashmap里的HashMap.Node一样,
这是读源码的一个好处吧。
- public class MyBST<C extends Comparable<?>> {
- static class Node implements Comparable,Cloneable{
- Node parent;//父类节点
- Node left;//左子树节点
- Node right;//右子树节点
- Comparable value;//实现了Comparable的value
- public Node(Node parent, Comparable value, Node left, Node right){
- this.parent=parent;
- this.left=left;
- this.right=right;
- this.value=value;
- }
- }
- }
2.增加
增加的代码不是很难写
- public boolean add(C c){
- if(root==null){
- root = new MyBST.Node(null,c,null,null);
- }else{
- Node node = root;
- Node nodeParent = root;
- boolean isNodeLeft = false;
- //按大左小右,直到node为空,nodeParent 就是要插入的父节点了,
- //注意isNodeLeft来判断到底是插入nodeParent.right还是nodeParent.left
- while(node!=null){
- nodeParent = node;
- if(node.value.compareTo(c)>0){
- //should put root.left
- node=node.left;
- isNodeLeft = true;
- }else if(node.value.compareTo(c)<0){
- //should put root.right
- node=node.right;
- isNodeLeft = false;
- }else{
- System.out.println("can‘t add duplicate value");
- return false;
- }
- }
- node = new MyBST.Node(nodeParent,c,null,null);
- if(isNodeLeft)
- nodeParent.left = node;
- else
- nodeParent.right = node;
- }
- return true;
- }

3.遍历
只写了深度优先的前序遍历,中序遍历,后序遍历。
算法有递归和非递归2种算法。递归很简单,非递归就比较麻烦,特别是后续遍历的非递归。
算法的理解参照
http://blog.csdn.net/pi9nc/article/details/13008511/
感谢这位作者的分享,我在看了
算法的基础上以我理解的方式用 java来写
【先序遍历】
- //先序遍历递归写法 【根节点-左子树-右子树】
- public void preTravel_recrusive(MyBST.Node node){
- if(node==null)
- return;
- System.out.println(node.value);
- if(node.left!=null){
- preTravel_recrusive(node.left);
- }
- if(node.right!=null){
- preTravel_recrusive(node.right);
- }
- }
- //先序遍历非递归写法 借助了stack这个先进后出的数据结构
- public void preTravel(){
- Stack<Node> stack = new Stack<Node>();
- if(this.root==null)
- return;
- Node current = this.root;
- //先把root压入栈顶
- stack.push(current);
- while(current!=null || !stack.isEmpty()){
- if(current!=null){
- System.out.println(current.value);
- current = current.left;
- }else{
- current = stack.pop();
- current = current.right;
- }
- if(current!=null)
- stack.push(current);
- }
- }

【中序遍历】
//中序遍历 【左子树-根节点-右子树】
- public void midTravel_recrusive(MyBST.Node node){
- if(node==null)
- return;
- if(node.left!=null){
- midTravel_recrusive(node.left);
- }
- System.out.println(node.value);
- if(node.right!=null){
- midTravel_recrusive(node.right);
- }
- }
- //中序遍历非递归写法 借助了stack这个先进后出的数据结构
- public void midTravel(){
- Stack<Node> stack = new Stack<Node>();
- Node node = this.root;
- if(node==null)
- return;
- stack.push(node);
- //如果node为空,就要去stack里判断是否为空
- while(node!=null || !stack.isEmpty()){
- if(node!=null){
- node = node.left;
- }else{
- node = stack.pop();
- System.out.println(node.value);
- node = node.right;
- }
- if(node!=null)
- stack.push(node);
- }
- }

【后序遍历】
- //后序遍历 【左子树-右子树-根节点】
- public void behideTravel_recrusive(MyBST.Node node){
- if(node==null)
- return;
- if(node.left!=null){
- behideTravel_recrusive(node.left);
- }
- if(node.right!=null){
- behideTravel_recrusive(node.right);
- }
- System.out.println(node.value);
- }
-
- //非递归后序遍历,这个发了我很长时间调试。
- //主要是理解算法和原理,方向对了,剩下的就是不断的测试各种可能性
- public void behideTravel(){
- if(this.root==null){
- return ;
- }
- Stack<Node> stack = new Stack<Node>();
- Node node=null,cur=this.root,pre=null;
- stack.add(cur);
- while(!stack.isEmpty()){
- node=null;
- //注意pre要!=null
- if(cur.right!=null && !(pre!=null && (cur.left==pre||cur.right==pre))){
- stack.add(cur.right);
- node = cur.right;
- }
- //注意pre要!=null
- if(cur.left!=null && !(pre!=null && (cur.left==pre||cur.right==pre))){
- stack.add(cur.left);
- node =cur.left;
- }
- if(node!=null)
- cur = node;
- else{
- pre = cur;
- cur = stack.peek();
- //注意pre要!=null
- if( (cur.right==null || cur.left==null) ||
- (pre!=null && (cur.left==pre||cur.right==pre))
- ){
- System.out.println(cur.value);
- cur = stack.pop();
- }
- }
- }
- }

4.删除
- public boolean delete(C c){
- Node deleteNode = root;
- //isLeft 删除节点是它的父类的左还是右
- boolean isLeft = false;
- while(deleteNode!=null){
- if(deleteNode.value.compareTo(c)>0){
- deleteNode = deleteNode.left;
- isLeft = true;
- }else if (deleteNode.value.compareTo(c)<0){
- deleteNode = deleteNode.right;
- isLeft = false;
- }else{
- break;
- }
- }
- if(deleteNode==null)
- return false;
- else{
- if(deleteNode.left==null && deleteNode.right==null){//删除的节点是叶子节点
- if(deleteNode.parent==null){//注意头节点
- root = null;
- return true;
- }
- if(isLeft){
- deleteNode.parent.left=null;
- }else{
- deleteNode.parent.right=null;
- }
- deleteNode.parent=null;
- }else if(deleteNode.left!=null && deleteNode.right==null){//删除的节点有left
- if(deleteNode.parent==null){//delete node is root
- root = deleteNode.left;
- }else{
- deleteNode.parent.left=deleteNode.left;
- deleteNode.left.parent=deleteNode.parent;
- }
- }else if(deleteNode.right!=null && deleteNode.left==null){//删除的节点有right
- if(deleteNode.parent==null){//delete node is root
- root = deleteNode.right;
- }else{
- deleteNode.parent.right=deleteNode.right;
- deleteNode.right.parent=deleteNode.parent;
- }
- }else{//have right and left child tree
- Node successor = deleteNode.right;
- // 从删除的节点的右子树里找到最小的值,作为删除节点的父节点的左或右子树
- //(依据于删除节点原来是父节点的左或右)
- while(successor.left!=null){
- successor=successor.left;
- }
- if(isLeft){
- successor.parent.left = successor.right;
- }else{
- successor.parent.right = successor.right;
- }
- if(successor.right!=null){
- successor.right.parent=successor.parent;
- }
-
- if(deleteNode.parent==null){//注意删除的节点是头节点
- root = successor;
- }else{
- if(isLeft){
- deleteNode.parent.left=successor;
- }else{
- deleteNode.parent.right=successor;
- }
- }
- successor.right=deleteNode.right;
- successor.left=deleteNode.left;
- successor.parent=deleteNode.parent;
- }
- deleteNode.parent=null;
- deleteNode.right=null;
- deleteNode.left=null;
- return true;
- }
- }

在测试的时候要注意各种可能性,多测各种临界条件。
代码在
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/菜鸟追梦旅行/article/detail/306663
推荐阅读
相关标签


