数据结构面试常见问题：什么是二叉树？如何进行二叉树的遍历？_什么是二叉树?如何遍历一个二叉树?

二叉树的介绍

二叉树是一种特殊的数据结构，它的每个元素都有零个、一个或两个子元素。这些元素被称为节点，每个节点都有一个值，以及两个指向其子节点的链接。

这种结构就像一个家族树，每个节点都有一个父节点（除了顶部的根节点），以及左右两个子节点。在实际项目中，我们经常会用到二叉树这种数据结构，它在数据存储、搜索等方面都有着广泛的应用。

接下来，我们将深入探讨二叉树的结构，包括节点、父节点、子节点、叶节点、根节点等概念。

二叉树的结构

二叉树由多个节点组成，每个节点最多有两个子节点，分别称为左子节点和右子节点。节点上的数据称为节点的值。没有子节点的节点称为叶节点，有子节点的节点称为父节点。在一棵二叉树中，有一个特殊的节点，它没有父节点，我们称它为根节点。

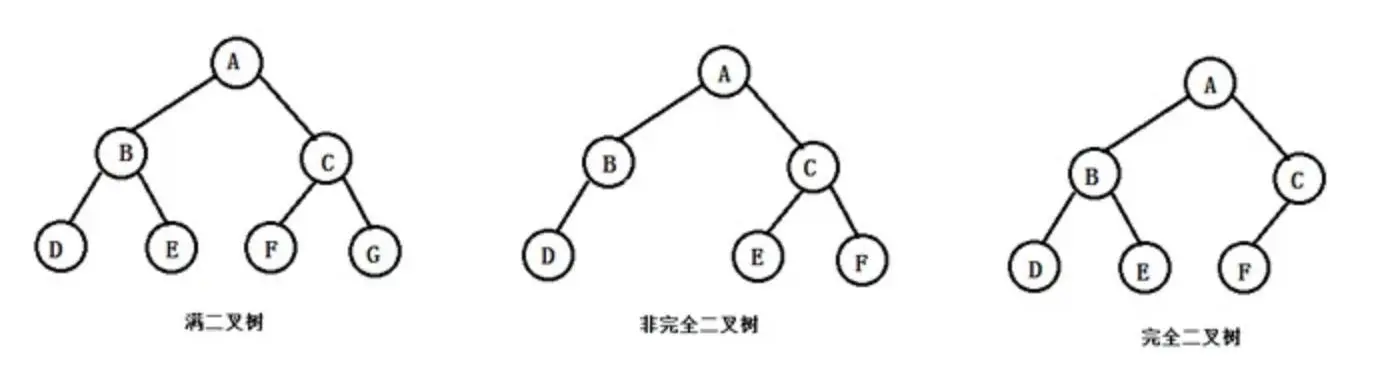
二叉树有很多特殊的类型，比如完全二叉树、满二叉树等。完全二叉树是指除了最后一层外，其他层的节点都是满的，而且最后一层的节点都集中在左边。满二叉树是每一层的节点都是满的。

接下来，我们将开始介绍二叉树的前序遍历。

二叉树的前序遍历

前序遍历是一种遍历二叉树的方法，它的顺序是：根节点 -> 左子树 -> 右子树。这种遍历方式应用在各种场景中，例如在文件系统的目录结构展示，或者在某些特定的算法中，如语法分析，都有它的身影。

下面我们将通过一个Java代码示例讲解二叉树的前序遍历。在这个示例中，我们定义了一个名为OneMoreNode的二叉树节点类，包含了节点的值和左右子节点。然后，我们定义了一个前序遍历的方法，该方法首先打印当前节点的值，然后递归地遍历左子树和右子树。

class OneMoreNode {
    int value;
    OneMoreNode left;
    OneMoreNode right;

    OneMoreNode(int value) {
        this.value = value;
    }
}

public void preOrder(OneMoreNode node) {
    if (node == null) {
        return;
    }
    System.out.println(node.value);
    preOrder(node.left);
    preOrder(node.right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

通过这个简单的示例，我们可以看到前序遍历的实现并不复杂，但是它却能够帮我们有效地遍历二叉树。接下来，我们将介绍二叉树的另一种遍历方式——中序遍历。

二叉树的中序遍历

在前文我们已经了解了二叉树的前序遍历，那么接下来，我们要探讨的是二叉树的另一种遍历方式——中序遍历。中序遍历是二叉树遍历方式中最为特殊的一种，它的特点是先访问左子树，然后访问根节点，最后访问右子树。因此，对于一个二叉树，我们可以通过中序遍历得到一个升序的序列，这也是中序遍历在实际应用中的一个重要作用。

接下来，我们通过Java代码示例来看一下如何实现二叉树的中序遍历。假设我们有一个名为OneMoreNode的二叉树节点类，该类包含了value、left和right三个属性，分别代表节点的值，左子节点和右子节点。

class OneMoreNode {
    int value;
    OneMoreNode left;
    OneMoreNode right;

    OneMoreNode(int value) {
        this.value = value;
    }
}
1
2
3
4
5
6
7
8
9

我们可以使用递归的方式来实现二叉树的中序遍历：

public void inorderTraversal(OneMoreNode node) {
    if (node == null) {
        return;
    }

    inorderTraversal(node.left);
    System.out.println(node.value);
    inorderTraversal(node.right);
}
1
2
3
4
5
6
7
8
9

在这段代码中，我们首先判断当前节点是否为空，如果为空则直接返回。然后，我们递归地对左子树进行中序遍历，打印当前节点的值，最后递归地对右子树进行中序遍历。这就是二叉树中序遍历的基本思想。

了解了二叉树的中序遍历，我们接下来将介绍二叉树的后序遍历。

二叉树的后序遍历

在前序遍历和中序遍历的基础上，我们来探索二叉树的后序遍历。后序遍历是一种更为深入的遍历方式，它的遍历顺序是左子树——右子树——根节点。在某些特定的应用场景中，后序遍历有着独特的优势。比如，在计算一个表达式树的值时，我们需要先计算左右子树（即操作数），然后再计算根节点（即操作符）。

让我们通过一个Java代码示例来具体了解一下如何实现后序遍历。假设我们有一个名为OneMoreNode的二叉树节点类，它有左右子节点和一个存储值的字段。

class OneMoreNode {
    OneMoreNode left;
    OneMoreNode right;
    int value;

    OneMoreNode(int value) {
        this.value = value;
    }
}
1
2
3
4
5
6
7
8
9

我们可以使用递归的方式来实现后序遍历：

void postOrderTraversal(OneMoreNode node) {
    if (node == null) {
        return;
    }

    postOrderTraversal(node.left);
    postOrderTraversal(node.right);
    System.out.println(node.value);
}
1
2
3
4
5
6
7
8
9

在这个函数中，我们首先检查当前节点是否为空，如果为空则直接返回。然后，我们对左子树进行后序遍历，接着对右子树进行后序遍历，最后访问当前节点。这就是后序遍历的实现方式。

通过这个例子，我希望你能理解后序遍历的基本思想和实现方式。在实际编程中，理解并掌握这些二叉树的遍历方式，将对你解决复杂问题有很大的帮助。

总结

在本文中，我们介绍了二叉树的基本结构，以及前序遍历、中序遍历和后序遍历的实现方式。每一种遍历方式都有其独特的应用场景，理解它们的工作原理和实现方式，将帮助我们在实际编程中更有效地解决问题。

二叉树的魅力并不仅仅在于它的结构，更在于它如何帮助我们解决复杂的问题。它就像一个微缩的世界，每一个节点都是一个独立的个体，但又与其他节点紧密相连，共同构建了这个世界。

我们可以将二叉树看作是一种工具，帮助我们更好地理解和解决问题。但同时，它也是一种哲学，它教会我们如何看待世界，如何处理复杂性，如何将大问题分解成小问题。

我们的学习之旅还在继续，二叉树只是我们的一个起点。让我们一起继续前行，探索编程世界的更多奥秘。