C++的实用工具——筛法

很多c++的算法都有不同的解法，本人精心挑选了最有的解法，今天就来讲一下筛法

埃氏筛

埃氏筛的原理其实很简单，在小学五年级是也会学到这一解法。

步骤

1. 定义一个bool类型的数组，用数组下标表示哪个数，里面存1和0,1表示是素数，0表示不是素数。
2. 先把数组全部初始化为1，可以用memset
3. 从2开始枚举到任意一个数（范围）如果这个数据为1，就说明它是素数，把它的下标的倍数的值全部设为0

代码

#include<bits/stdc++.h>
#define int long long
int count_ss,T;
bool ss[2000005];
void sushu(){
    for(int i=2;i<=2000000;i++){
        if(ss[i]){
            count_ss++;//可以顺便记录一下素数个数
            for(int j=i*2;i*j<=2000000;j+=i){
                ss[j]=0;
            }
        }
    }
}
signed main(){
    memset(ss,1,sizeof(ss));
    sushu();
    return 0;
}

相关题目

大家可以用埃氏筛做很多题，比如P8319 『JROI-4』分数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

欧拉筛（或线性筛）

我们发现埃氏筛还是有很多重复的筛过的，例如 30=3*10=2*15 所以我们思考优化筛过的重复的，

通过 最小质因数 * 数字，我们发现我们每个数都有一个最小质因数，假设我们使用他来做数字的标记，我们就可以达到每个数字只被筛选一次。时间复杂度是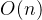

代码

//变量解释：vis[i]为bool类型，表示i是不是素数
//pri[i]为int类型，表示第i个素数
//maxn为筛法范围
void init(){
	for (int i=2;i<MAXN;i++){
		if(!vis[i]){
			pri[++cnt]=i;
		}
		for(int j=1;j<=cnt;j++) {
			if(i*pri[j]>=MAXN)break;
			vis[i*pri[j]]=1;
			if(i%pri[j]==0){
	// i % pri[j] == 0
	// 换言之，i 之前被 pri[j] 筛过了
	// 由于 pri 里面质数是从小到大的，所以 pri[j]就是 i 的最小质因数，同时也是 i *pri[j] 的最小质因数
	// 那么再拿 pri[j + 1] 去筛，pri[j] 是 i * prime[j + 1] 的最小质因数，不符合题目要求
				break;
			}
		}
	}
}

相关题目

[传智杯 #4 初赛] 小卡与质数 2 - 洛谷

ps

记得点个关注哦！