【A星算法】A星A*寻路算法详解（小白一看就懂+C#代码+零基础学习A*）

1.问题背景

在制作RPG游戏角色和NPC移动时，需要角色自动避开障碍物，到达终点
怎么快速找到一条到达终点的路径？
使用a星寻路算法

2.A星算法的思路

绿色：起点；红色：终点 ；黑色：障碍物
新增的浅绿方块为当前评估节点
对角线的代价为14.14
直线代价为10

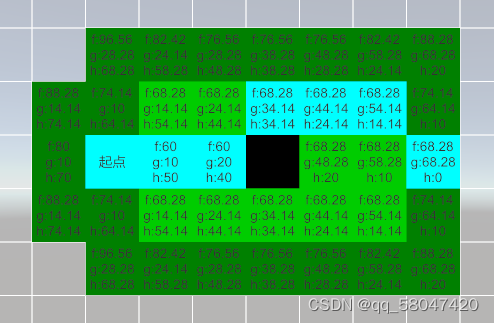
基本概念：

f = g + h
f： 总评估代价
g：起点到当前点的代价
h：当前点到终点的预期（或理想）代价（如果当前评估点到终点的直线上没有障碍物，则当前的总代价f不会改变）
将总代价f作为权重，每次优先遍历最小的f节点
a星算法，会在开表中寻找总花费最小的节点为评估点，遍历当前评估点附近点，在附近点，选择总代价最小的点作为评估点的下一节点

1.初始化起点，终点；将起点放入开表，作为评估点，在开表中选择总代价最小的作为评估节点，如果评估节点为终点，则结束
2.将当前的节点移除开表，放入闭表中（将当前的节点标记为已评估节点）
3.先遍历评估节点周围8个点（上下左右，左上角，右上角，左下角，右下角）,将它们放入一个临近点集合中
4.遍历临近点集合，如果闭表已经有该点（该点已经被评估过）或者该点是障碍物，跳过该点
5. 计算 邻近点到起点总花费newcost=当前到邻近点的距离+当前点到起点的花费
6. 1)newGCost 小于之前计算的Gost，说明该点已经被遍历过，在开表中，
说明之前的路径存在绕远路，将邻近点的上一节点改为当前点,计算邻近点的f,g,h花费
2)开表中不包含该邻近点，该节点没有被遍历，不在开表，将邻近点的上一节点改为当前点，
加入开表，计算邻近点的f,g,h花费
7.重复1
上面的过程，如果看不太懂，后面核心代码实现，有代码和注释
距离的计算
给定两个坐标，计算两个坐标的路径距离
代码 创建APathNode类

3.代码实现

public class APathNode : IComparable<APathNode>
{
    public int X;
    public int Z;
    public bool available;//如果是障碍物为false
    public float GCost = 0;//起点到当前点的花费
    public float HCost = 0;//当前点到终点的预期花费
    public float TotalCost = 0;//总花费
    public APathNode LastNode;//上一个节点
    public int CompareTo(APathNode other)//使用最小堆排序,要实现IComparable<APathNode>接口
    {
        if (this.TotalCost>other.TotalCost)
        {
            return 1;
        }
        else if (other.TotalCost == this.TotalCost)
        {
            return 0;
        }
        else
        {
            return -1;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

代码，创建AStarSearchPath类，下面代码均属于该类
计算两点的距离

public float GetCostByDistance(APathNode currentNode,APathNode neighborNode)
    {
        float cost = 0;
        int Horizontal = Math.Abs(currentNode.X - neighborNode.X);
        int Vertical = Math.Abs(currentNode.Z - neighborNode.Z);
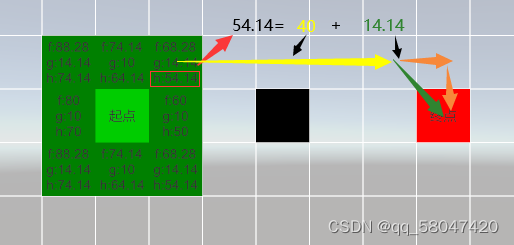
        int line = Math.Min(Horizontal, Vertical);//对应上图一个橙色箭头
        
        int brokenline = Horizontal + Vertical;//折线
        //CurveCostWeigh=14.14f,LineCostWeight=10f
        //cost=        曲线价值      + 直线价值 
        //cost=        曲线价值   +  brokenline(1黄+2橙)-2*line（橙）
        cost = line * CurveCostWeigh+(brokenline-2*line)*LineCostWeight;
        return cost;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

寻找附近的邻近点

private List<APathNode> GainNeighborNode(APathNode currentNode)
    {
        List<APathNode> neighborNodes = new List<APathNode>();
        for (int i = -1; i <2 ; i++)
        {
            for (int j = -1; j < 2; j++)
            {
                if(i==0&&j==0) continue;//排除当前节点
                int x = currentNode.X + i;
                int z = currentNode.Z + j;
                if (x >= 0 && x < width && z >= 0 && z < height)
                {
                    neighborNodes.Add(Map[z, x]);//在范围的邻近点加入集合
                }
            }
        }
        return neighborNodes;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

得到最后的寻路节点集合

private void RetracePath()
    {
        FinalPaths = new List<APathNode>();
        APathNode point = EndPathNode;
        while (point!=null)
        {
            FinalPaths.Add(point);
            point = point.LastNode;
        }
    }
1
2
3
4
5
6
7
8
9
10

寻路方法核心代码

public void SearchPath()
    {
         //将起点加入开表
        OpenList.Add(StartPathNode);//APathNode
        while(OpenList.Count>0)
        {
            //currentNode = FindMinExpectCost();//寻找总花费最小节点
            currentNode = OpenList.Dequeue();//取出第一元素,在开表中删除
            //将当前的节点移除开表，放入闭表中（将当前的节点标记为已评估节点）
            //OpenList.Remove(currentNode);删除
            CloseList.Add(currentNode);
            //如果评估点等于终点，结束寻路
            if (currentNode == EndPathNode)
            {
                RetracePath();
                //找到寻路路径
                Debug.Log("---找到了");
                return;
            }
            else
            {
                //遍历评估节点周围8个点（上下左右，左上角，右上角，左下角，右下角）
                List<APathNode> neighborNodes = GainNeighborNode(currentNode);
                for (int i = 0; i < neighborNodes.Count; i++)
                {
                     //如果闭表已经有该点（该点已经被评估过）或者该点是障碍物
                    if (CloseList.Contains(neighborNodes[i]) || !neighborNodes[i].available)
                    {
                        continue;
                    }
                    //新的 起点->neighbor =当前点->邻近点 +当前点->起点
                    //计算 该邻近点到起点总花费=当前到邻近点的距离+当前点到起点的花费
                    float newGCost = GetCostByDistance(currentNode, neighborNodes[i]) + currentNode.GCost;
                    //1.如果邻近点到起点总花费<之前已计算的花费，说明之前的路径存在绕远路，将邻近点的上一节点改为当前点
                    //因为计算过邻近点Gcost，所有一定存在开表中，后面值为false
                    //2》.开表中不包含邻近点，该节点没有被遍历
                    if (newGCost < neighborNodes[i].GCost || !OpenList.Contains(neighborNodes[i]))
                    {
                       //更新邻近点的三大代价，将邻近点的上一节点设置为当前节点
                        neighborNodes[i].GCost = newGCost;
                        neighborNodes[i].HCost = GetCostByDistance(neighborNodes[i], EndPathNode);
                        neighborNodes[i].TotalCost = neighborNodes[i].GCost + neighborNodes[i].HCost;
                        neighborNodes[i].LastNode = currentNode;
                        if (!OpenList.Contains(neighborNodes[i]))
                        {
                            OpenList.Add(neighborNodes[i]);//2》.如果开表中不包含邻近点，该节点没有被遍历
                        }
                    }
                }
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

代码初始化地图大小，障碍物坐标，起点终点坐标

public void initMapData2(Vector2 startPoint,Vector2 endPoint,Vector2 rect, GameObject root=null)
    {
        this.startPoint = startPoint;
        this.endPoint = endPoint;
        //初始化地图高度，宽度
        this.width = (int)rect.x;
        this.height = (int)rect.y;
        if (startPoint.x <= 0 || startPoint.x > width||startPoint.y <= 0 || startPoint.y > height)
        {
            throw new Exception("输入的startPoint超出范围");
        }
        if (endPoint.x <= 0 || endPoint.x > width||endPoint.y <= 0 || endPoint.y > height)
        {
            throw new Exception("输入的endPoint超出范围");
        }
        Map = new APathNode[height, width];
        for (int i = 0; i <height; i++)
        {
            for (int j = 0; j < width; j++)
            {
                #region 基于自己的规则设置障碍物
                GameObject c=root.transform.GetChild((i*width)+j).gameObject;
                Map[i, j] = new APathNode();
                Map[i, j].X = j;
                Map[i, j].Z = i;
                Color color = c.GetComponent<MPImage>().color;
                if (color.r<=0&&color.g<=0&&color.b<=0)
                #endregion 基于自己的规则设置障碍物
                {
                    Debug.Log("false");
                    Map[i, j].available = false;
                }
                else
                {
                    Debug.Log("true");
                    Map[i, j].available = true;
                }
            }
        }
        StartPathNode = new APathNode();
        EndPathNode = new APathNode();
        StartPathNode = Map[(int)startPoint.y, (int)startPoint.x];
        EndPathNode = Map[(int)endPoint.y, (int)endPoint.x];
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

AStarSearchPath类的属性

    public float LineCostWeight = 10f;
    public float CurveCostWeigh = 14.14f;
    //public List<APathNode> OpenList=new List<APathNode>();
    public PriorityQueue<APathNode> OpenList=new PriorityQueue<APathNode>();//使用最小堆排序,要实现IComparable<APathNode>接口
    public List<APathNode> CloseList=new List<APathNode>();
    public APathNode currentNode;
    public APathNode[,] Map;
    public APathNode StartPathNode;
    public APathNode EndPathNode;
    public int width;
    public int height;
    public List<APathNode> FinalPaths=new List<APathNode>();
1
2
3
4
5
6
7
8
9
10
11
12

4.结束语

希望上面的代码对大家有所帮助，有疑问的地方可以在评论区留言

优化和扩展

平滑路径，生成路径不平滑，删除无用的节点
A星寻路尽管相对于其他算法，效率比较高，但是当地图节点，比较多时，花费时间还是比较多
最小堆，可以优化在openlist开表中取最小花费的时间
拐点算法，只寻找关键的拐点
权重引导寻路，f=g+h+w,权重存储在AStarSearchPath的Map中，提前设置权重小的节点，寻路时，会沿着提前设置的节点寻路
编写地图编辑器，基于游戏引擎，在场景中设置障碍物，用图片保存
如果大家想学习更多的扩展，麻烦大家点赞评论收藏，支持一下，如果有很多人想学习，考虑出更多的关于A星的扩展

补充

实现最小堆排序
增加了PriorityQueue类,修改了AStarSearchPath的OpenList,SearchPath方法currentNode = OpenList.Dequeue();替换了currentNode = FindMinExpectCost();OpenList.Remove(currentNode);

public class PriorityQueue<T> where T : IComparable<T>
{
    private List<T> data;

    public PriorityQueue()
    {
        this.data = new List<T>();
    }
    public void Clear()
    {
        data.Clear();
    }
    public bool Contains(T item)
    {
        return data.Contains(item);
    }
    /// <summary>
    /// 增加数据到优先队列
    /// </summary>
    /// <param name="item"></param>
    public void Add(T item)
    {
        data.Add(item);//加入到完全二叉树的末尾,新节点依次向上比较父节点
        int childIndex = data.Count - 1;
        while (childIndex > 0)
        {
            int parentIndex = (childIndex - 1) / 2;//根据规律,获取父节点
            if (data[childIndex].CompareTo(data[parentIndex]) >= 0)//子节点大于父节点,满足最小堆定义,结束
                break;
            T temp = data[childIndex];//子节点小于父节点,交换父子节点
            data[childIndex] = data[parentIndex];
            data[parentIndex] = temp;
            childIndex = parentIndex;//子节点等于父节点
        }
    }
    /// <summary>
    /// 取出并删除顶部数据
    /// </summary>
    /// <returns></returns>
    public T Dequeue()
    {
        T item = data[0];//暂存第一个
        int lastIndex = data.Count - 1;
        data[0] = data[lastIndex];
        data.RemoveAt(lastIndex);
        --lastIndex;
        int parentIndex = 0;
        while (true)
        {
            int childIndex = parentIndex * 2 + 1;
            if (childIndex > lastIndex)
            {
                break;//左子节点在范围内
            }
            int rightIndex = childIndex + 1;
            if (rightIndex <= lastIndex && data[rightIndex].CompareTo(data[childIndex]) < 0)
            {
                childIndex = rightIndex;//选择左右最小的子节点,且右节点在范围内
            }
            if (data[parentIndex].CompareTo(data[childIndex]) <= 0)
            {
                break;//父节点比子节点小,满足最小堆,结束
            }
            T temp = data[parentIndex];
            data[parentIndex] = data[childIndex];
            data[childIndex] = temp;
            parentIndex = childIndex;//父节点等于子节点索引
        }
        return item;
    }
    public T Peek()
    {
        return data[0];
    }
    public int Count
    {
        get
        {
            return data.Count;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82