机器人在笛卡尔空间和关节空间的多项式轨迹规划以及matlab代码（三次、五次、七次）_三次多项式轨迹规划

三次多项式轨迹规划：

三次多项式轨迹规划就是s(t)相对于时间t的变化满足三次多项式变化，其表达式如下：

                    

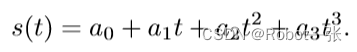
如前文所述：t的取值范围是[0,T],s(t)的取值范围是[0,1], 又因为初始速度和末速度都为0，所以：

S（t）的一阶导数表达式为：

从而可以计算出对应的系数：

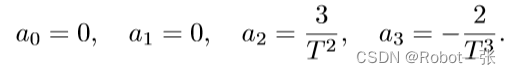
将系数带入到上面的三次多项式，可得到

再将上式代入到路径表达式，即可得到完整的轨迹规划表达式，如下所示：

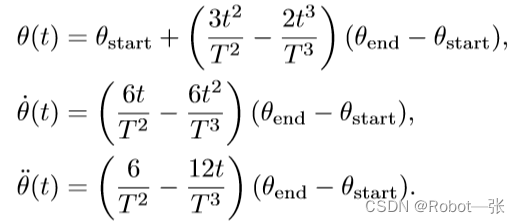
其中，最大的关节速度在 时刻到达，其数值为：

最大的关节加速度和关节减速度在 和 ，其中：

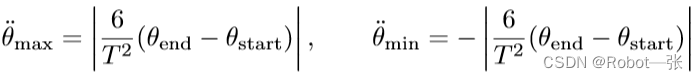
关节空间三次多项式轨迹规划：

TH1=[30,60,2,5,50,70,80]; %定义关节空间中的两个点TH1,TH2.
TH2=[90,54,3,60,80,40,60];
T=1;%定以一个时间，即从TH1到TH2的总时间。
TH=[];
TH_yijie=[];
TH_erjie=[];
TT=[];%定以四个变量TH、TH_yijie、TH_erjie、TT，用来储存数据
for t=0:0.001:T  
    th=TH1+(TH2-TH1)*(3*t^2/T^2-2*t^3/T^3);%角度和时间变化关系
    th_yijie=(TH2-TH1)*(6*t/T^2-6*t^2/T^3);%角速度和时间变化关系
    th_erjie=(TH2-TH1)*(6/T^2-12*t/T^3);%角加速度和时间变化关系
    TH=[TH,th'];
    TH_yijie=[TH_yijie,th_yijie'];
    TH_erjie=[TH_erjie,th_erjie'];
    TT=[TT,t];
end
TH=TH';%矩阵转置
TH_yijie=TH_yijie';
TH_erjie=TH_erjie';
TT=TT';
fig1=figure;
plot(TT,TH(:,1));%三维绘图此处绘制一轴关节角度变化示意。
grid on;
fig2=figure;
plot(TT,TH_yijie(:,1));%三维绘图此处绘制一轴关节角速度变化示意。
grid on;
fig3=figure;
plot(TT,TH_erjie(:,1));%三维绘图此处绘制一轴关节角加速度变化示意。
grid on;

笛卡尔空间三次多项式轨迹规划：

A=[30,60,2]; %定义笛卡尔空间中的两个点A,B.
B=[90,54,3];
T=1;%定义一个时间，即从A到B的总时间。
X=[];
X_yijie=[];
X_erjie=[];
TT=[];%定以四个变量X、X_yijie、X_erjie、TT，用来储存数据
for t=0:0.001:T  
    x=A+(B-A)*(3*t^2/T^2-2*t^3/T^3);%角度和时间变化关系
    x_yijie=(B-A)*(6*t/T^2-6*t^2/T^3);%角速度和时间变化关系
    x_erjie=(B-A)*(6/T^2-12*t/T^3);%角加速度和时间变化关系
    X=[X,x'];
    X_yijie=[X_yijie,x_yijie'];
    X_erjie=[X_erjie,x_erjie'];
    TT=[TT,t];
end
X=X';%矩阵转置
X_yijie=X_yijie';
X_erjie=X_erjie';
TT=TT';
fig1=figure;
plot(TT,X(:,1));%三维绘图此处绘制x方向位移变化示意。
grid on;
fig2=figure;
plot(TT,X_yijie(:,1));%三维绘图此处绘制x方向速度变化示意。
grid on;
fig3=figure;
plot(TT,X_erjie(:,1));%三维绘图此处绘制x方向加速度变化示意。
grid on;

五次多项式轨迹规划：

五次多项式轨迹规划就是s(t)相对于时间t的变化满足五次多项式变化，其表达式如下：

其中：

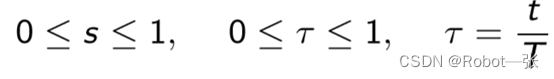
求出系数如下：

所以其运动方程如下：

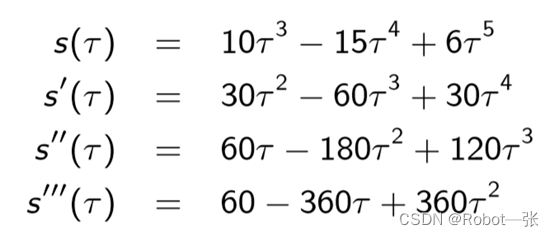
各个变量的最值如下：

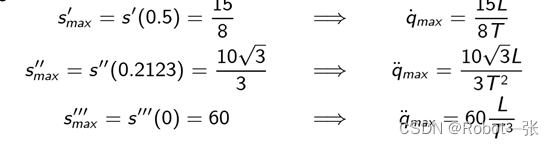
关节空间五次多项式轨迹规划：

TH1=[30,60,2,5,50,70,80]; %定义关节空间中的两个点TH1,TH2.
TH2=[90,54,3,60,80,40,60];
T=1;%定以一个时间，即从TH1到TH2的总时间。
TH=[];
TH_yijie=[];
TH_erjie=[];
TT=[];%定以四个变量TH、TH_yijie、TH_erjie、TT，用来储存数据
for t=0:0.001:T  
    th=TH1+(TH2-TH1)*(10*(t/T)^3-15*(t/T)^4+6*(t/T)^5);%角度和时间变化关系
    th_yijie=(TH2-TH1)*(30*(t/T)^2-60*(t/T)^3+30*(t/T)^4);%角速度和时间变化关系
    th_erjie=(TH2-TH1)*(60*(t/T)-180*(t/T)^2+120*(t/T)^3);%角加速度和时间变化关系
    TH=[TH,th'];
    TH_yijie=[TH_yijie,th_yijie'];
    TH_erjie=[TH_erjie,th_erjie'];
    TT=[TT,t];
end
TH=TH';%矩阵转置
TH_yijie=TH_yijie';
TH_erjie=TH_erjie';
TT=TT';
fig1=figure;
plot(TT,TH(:,1));%三维绘图此处绘制一轴关节角度变化示意。
grid on;
fig2=figure;
plot(TT,TH_yijie(:,1));%三维绘图此处绘制一轴关节角速度变化示意。
grid on;
fig3=figure;
plot(TT,TH_erjie(:,1));%三维绘图此处绘制一轴关节角加速度变化示意。
grid on;

笛卡尔空间五次多项式轨迹规划：

A=[30,60,2]; %定义笛卡尔空间中的两个点A,B.
B=[90,54,3];
T=1;%定义一个时间，即从A到B的总时间。
X=[];
X_yijie=[];
X_erjie=[];
TT=[];%定以四个变量X、X_yijie、X_erjie、TT，用来储存数据
for t=0:0.001:T  
    x=A+(B-A)*(10*(t/T)^3-15*(t/T)^4+6*(t/T)^5);%角度和时间变化关系
    x_yijie=(B-A)*(30*(t/T)^2-60*(t/T)^3+30*(t/T)^4);%角速度和时间变化关系
    x_erjie=(B-A)*(60*(t/T)-180*(t/T)^2+120*(t/T)^3);%角加速度和时间变化关系
    X=[X,x'];
    X_yijie=[X_yijie,x_yijie'];
    X_erjie=[X_erjie,x_erjie'];
    TT=[TT,t];
end
X=X';%矩阵转置
X_yijie=X_yijie';
X_erjie=X_erjie';
TT=TT';
fig1=figure;
plot(TT,X(:,1));%三维绘图此处绘制x方向位移变化示意。
grid on;
fig2=figure;
plot(TT,X_yijie(:,1));%三维绘图此处绘制x方向速度变化示意。
grid on;
fig3=figure;
plot(TT,X_erjie(:,1));%三维绘图此处绘制x方向加速度变化示意。
grid on;

七次多项式轨迹规划：

五次多项式轨迹规划就是s(t)相对于时间t的变化满足五次多项式变化，其表达式如下：

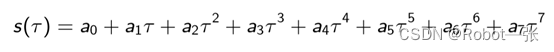
其中：

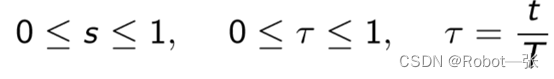
求出系数如下：  

所以其运动方程如下： 

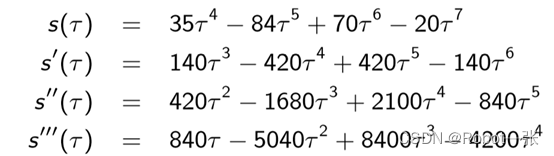
各个变量的最值如下： 

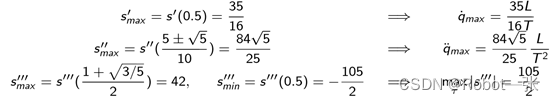
关节空间七次多项式轨迹规划：

TH1=[30,60,2,5,50,70,80]; %定义关节空间中的两个点TH1,TH2.
TH2=[90,54,3,60,80,40,60];
T=1;%定以一个时间，即从TH1到TH2的总时间。
TH=[];
TH_yijie=[];
TH_erjie=[];
TT=[];%定以四个变量TH、TH_yijie、TH_erjie、TT，用来储存数据
for t=0:0.001:T  
    th=TH1+(TH2-TH1)*(35*(t/T)^4-84*(t/T)^5+70*(t/T)^6-20*(t/T)^7);%角度和时间变化关系
    th_yijie=(TH2-TH1)*(140*(t/T)^3-420*(t/T)^4+420*(t/T)^5-140*(t/T)^6);%角速度和时间变化关系
    th_erjie=(TH2-TH1)*(420*(t/T)^2-1680*(t/T)^3+2100*(t/T)^4-840*(t/T)^5);%角加速度和时间变化关系
    TH=[TH,th'];
    TH_yijie=[TH_yijie,th_yijie'];
    TH_erjie=[TH_erjie,th_erjie'];
    TT=[TT,t];
end
TH=TH';%矩阵转置
TH_yijie=TH_yijie';
TH_erjie=TH_erjie';
TT=TT';
fig1=figure;
plot(TT,TH(:,1));%三维绘图此处绘制一轴关节角度变化示意。
grid on;
fig2=figure;
plot(TT,TH_yijie(:,1));%三维绘图此处绘制一轴关节角速度变化示意。
grid on;
fig3=figure;
plot(TT,TH_erjie(:,1));%三维绘图此处绘制一轴关节角加速度变化示意。
grid on;

笛卡尔空间七次多项式轨迹规划：

A=[30,60,2]; %定义笛卡尔空间中的两个点A,B.
B=[90,54,3];
T=1;%定义一个时间，即从A到B的总时间。
X=[];
X_yijie=[];
X_erjie=[];
TT=[];%定以四个变量X、X_yijie、X_erjie、TT，用来储存数据
for t=0:0.001:T  
    x=A+(B-A)*(35*(t/T)^4-84*(t/T)^5+70*(t/T)^6-20*(t/T)^7);%角度和时间变化关系
    x_yijie=(B-A)*(140*(t/T)^3-420*(t/T)^4+420*(t/T)^5-140*(t/T)^6);%角速度和时间变化关系
    x_erjie=(B-A)*(420*(t/T)^2-1680*(t/T)^3+2100*(t/T)^4-840*(t/T)^5);%角加速度和时间变化关系
    X=[X,x'];
    X_yijie=[X_yijie,x_yijie'];
    X_erjie=[X_erjie,x_erjie'];
    TT=[TT,t];
end
X=X';%矩阵转置
X_yijie=X_yijie';
X_erjie=X_erjie';
TT=TT';
fig1=figure;
plot(TT,X(:,1));%三维绘图此处绘制x方向位移变化示意。
grid on;
fig2=figure;
plot(TT,X_yijie(:,1));%三维绘图此处绘制x方向速度变化示意。
grid on;
fig3=figure;
plot(TT,X_erjie(:,1));%三维绘图此处绘制x方向加速度变化示意。
grid on;