决策树--信息增益,信息增益比,Geni指数的理解_头歌决策树答案
赞
踩
-
- 特征选择
- 决策树生成
- 决策树剪枝
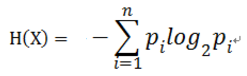
对于样本集合D来说,随机变量X是样本的类别,即,假设样本有k个类别,每个类别的概率是![]() ,其中|Ck|表示类别k的样本个数,|D|表示样本总数
,其中|Ck|表示类别k的样本个数,|D|表示样本总数
则对于样本集合D来说熵(经验熵)为:
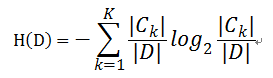
- 信息增益( ID3算法 )
定义: 以某特征划分数据集前后的熵的差值
在熵的理解那部分提到了,熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
- 解决方法 : 信息增益比( C4.5算法 )
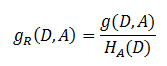
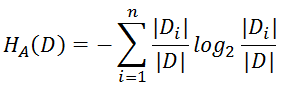
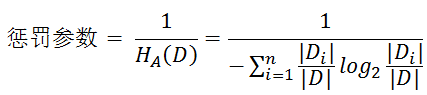
- 基尼指数( CART算法 ---分类树)
定义:基尼指数(基尼不纯度):表示在样本集合中一个随机选中的样本被分错的概率。
注意: Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。
即 基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率
书中公式:
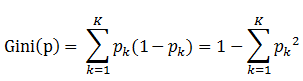
说明:
1. pk表示选中的样本属于k类别的概率,则这个样本被分错的概率是(1-pk)
2. 样本集合中有K个类别,一个随机选中的样本可以属于这k个类别中的任意一个,因而对类别就加和
3. 当为二分类是,Gini(P) = 2p(1-p)
样本集合D的Gini指数 : 假设集合中有K个类别,则:
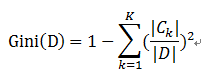
基于特征A划分样本集合D之后的基尼指数:
需要说明的是CART是个二叉树,也就是当使用某个特征划分样本集合只有两个集合:1. 等于给定的特征值 的样本集合D1 , 2 不等于给定的特征值 的样本集合D2
实际上是对拥有多个取值的特征的二值处理。
举个例子:
假设现在有特征 “学历”,此特征有三个特征取值: “本科”,“硕士”, “博士”,
当使用“学历”这个特征对样本集合D进行划分时,划分值分别有三个,因而有三种划分的可能集合,划分后的子集如下:
-
- 划分点: “本科”,划分后的子集合 : {本科},{硕士,博士}
- 划分点: “硕士”,划分后的子集合 : {硕士},{本科,博士}
- 划分点: “硕士”,划分后的子集合 : {博士},{本科,硕士}
对于上述的每一种划分,都可以计算出基于 划分特征= 某个特征值 将样本集合D划分为两个子集的纯度:
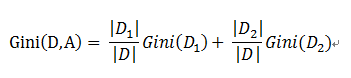
因而对于一个具有多个取值(超过2个)的特征,需要计算以每一个取值作为划分点,对样本D划分之后子集的纯度Gini(D,Ai),(其中Ai 表示特征A的可能取值)
然后从所有的可能划分的Gini(D,Ai)中找出Gini指数最小的划分,这个划分的划分点,便是使用特征A对样本集合D进行划分的最佳划分点。


