（2016/02/19）多传感器数据融合算法---9轴惯性传感器_卡尔曼九轴数据融合

2016年2月18日

传感器的原理

加速度计：

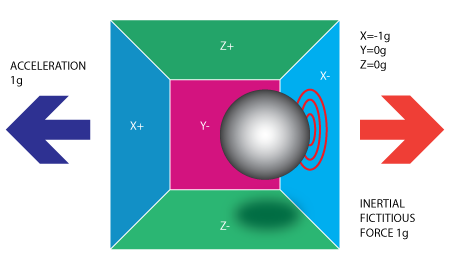
加速度计---我们可以把它想作一个圆球在一个方盒子中。

假定这个盒子不在重力场中或者其他任何会影响球的位置的场中，球处于盒子的正中央。

你可以想象盒子在外太空中，或远在航天飞机中，离任何天体，一切东西都处于无重力状态。

在图中你可以看到我们给每个轴分配了一对墙（我们移除了Y+以此来观察里面的情况）。

  

设想每面墙都能感测压力。如果我们突然把盒子向左移动（加速度为1g=9.8m/s^2），那么球会撞上X-墙。
然后我们检测球撞击墙面产生的压力，X轴输出值为-1g。


加速度计检测到力的方向与它本身加速度的方向是相反的。这种力量通常被称为惯性力。
在这个模型中，加速度计是通过间接测量力对一个墙面的作用来测量加速度的，在实际应用中，可能通过弹簧等装置来测量力。
这个力可以是加速度引起的，也不一定是加速度引起的。
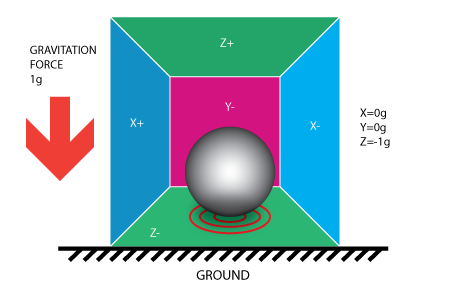
如果把模型放在地球上，球会落在Z-墙面上并对其施加一个1g的力。



在这种情况下盒子没有移动但我们任然读取到Z轴有-1g的值。球在墙壁上施加的压力是由引力造成的。
在理论上，它可以是不同类型的力量 - 例如，你可以想象我们的球是铁质的，将一个磁铁放在盒子旁边那球就会撞上另一面墙。引用这个例子只是为了说明加速度计的本质是检测力而非加速度。只是加速度所引起的惯性力正好能被加速度计的检测装置所捕获。

虽然这个模型并非一个MEMS传感器的真实构造，但它用来解决与加速度计相关的问题相当有效。
实际上有些类似传感器中有金属小球，它们称作倾角开关，但是它们的功能更弱，只能检测设备是否在一定程度内倾斜，却不能得到倾斜的程度。

到目前为止，我们已经分析了单轴的加速度计输出，这是使用单轴加速度计所能得到的。三轴加速度计的真正价值在于它们能够检测全部三个轴的惯性力。
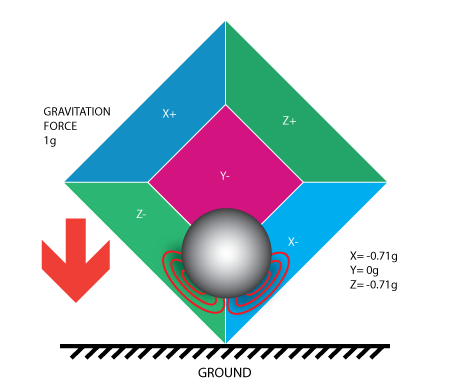
让我们回到盒子模型，并将盒子向右旋转45度。现在球会与两个面接触：Z-和X-，见下图：

0.71g这个值是不是任意的，它们实际上是1/2的平方根的近似值。我们介绍加速度计的下一个模型时这一点会更清楚。


在上一个模型中我们引入了重力并旋转了盒子。在最后的两个例子中我们分析了盒子在两种情况下的输出值，力矢量保持不变。
虽然这有助于理解加速度计是怎么和外部力相互作用的，但如果我们将坐标系换为加速度的三个轴并想象矢量力在周围旋转，这会更方便计算。



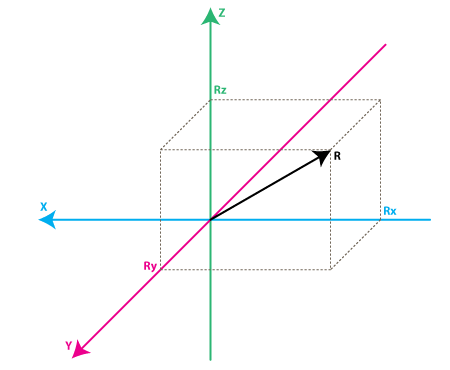
请看看在上面的模型，我保留了轴的颜色，以便你的思维能更好的从上一个模型转到新的模型中。
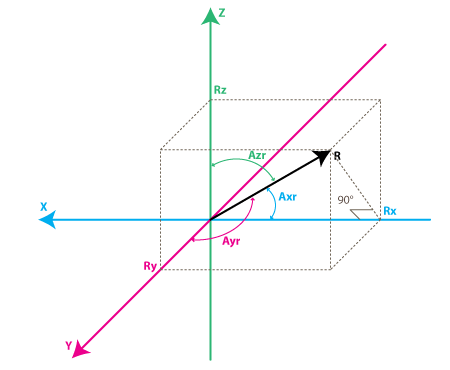
想象新模型中每个轴都分别垂直于原模型中各自的墙面。矢量R是加速度计所检测的矢量（它可能是重力或上面例子中惯性力的合成）。
RX，RY，RZ是矢量R在X，Y，Z上的投影。
请注意下列关系：
，R ^ 2 = RX ^ 2 + RY ^ 2 + RZ ^ 2（公式1）
此公式等价于三维空间勾股定理。

还记得我刚才说的1/2的平方根0.71不是个随机值吧。
如果你把它们代回上式，回顾一下重力加速度是1g，那我们就能验证：
1 ^ 2 =（SQRT（1/2））^ 2 + 0 ^ 2 +（SQRT（1/2））^ 2
在公式1中简单的取代： R=1, Rx = -SQRT(1/2), Ry = 0 , Rz = -SQRT(1/2)

经过一大段的理论序言后，我们和实际的加速度计很靠近了。RX，RY，RZ值是实际中加速度计输出的线性相关值，你可以用它们进行各种计算。

在我们运用它之前我们先讨论一点获取加速度计数据的方法。
大多数加速度计可归为两类：数字和模拟。
数字加速度计可通过I2C，SPI或USART方式获取信息，而模拟加速度计的输出是一个在预定范围内的电压值，你需要用ADC（模拟量转数字量）模块将其转换为数字值。
我将不会详细介绍ADC是怎么工作的，部分原因是这是个很广的话题，另一个原因是不同平台的ADC都会有差别。有些MCU具有内置ADC模块，而有些则需要外部电路进行ADC转换。
不管使用什么类型的ADC模块，你都会得到一个在一定范围内的数值。例如一个10位ADC模块的输出值范围在0 .. 1023间，请注意，1023 = 2 ^ 10 -1。
一个12位ADC模块的输出值范围在0 .. 4095内，注意，4095 = 2 ^ 12-1。

我们继续，先考虑下一个简单的例子，假设我们从10位ADC模块得到了以下的三个轴的数据：
AdcRx = 586
AdcRy = 630
AdcRz = 561

每个ADC模块都有一个参考电压，假设在我们的例子中，它是3.3V。要将一个10位的ADC值转成电压值，我们使用下列公式：
VoltsRx = AdcRx * VREF / 1023
小注：8位ADC的最大值是255 = 2 ^ 8 -1，12位ADC最大值是4095 = 2 ^ 12 -1。
将3个轴的值代入上式，得到：
VoltsRx = 586 * 3.3 / 1023 =～1.89V（结果取两位小数）
VoltsRy = 630 * 3.3 / 1023 =～2.03V
VoltsRz = 561 * 3.3 / 1023 =～1.81V
每个加速度计都有一个零加速度的电压值，你可以在它的说明书中找到，这个电压值对应于加速度为0g。
通过计算相对0g电压的偏移量我们可以得到一个有符号的电压值。比方说，0g电压值 VzeroG= 1.65V，通过下面的方式可以得到相对0g电压的偏移量:
DeltaVoltsRx = 1.89V - 1.65V = 0.24V
DeltaVoltsRy = 2.03V - 1.65V = 0.38V
DeltaVoltsRz = 1.81V - 1.65V = 0.16V

现在我们得到了加速度计的电压值，但它的单位还不是g（9.8m/s^2），
最后的转换，我们还需要引入加速度计的灵敏度（Sensitivity），单位通常是 mV/g。
比方说，加速度计的灵敏度 Sensitivity= 478.5mV / g = 0.4785V /g。
灵敏度值可以在加速度计说明书中找到。要获得最后的单位为g的加速度，我们使用下列公式计算：
RX = DeltaVoltsRx /Sensitivity
RX = 0.24V / 0.4785V / G =～0.5g
RY = 0.38V / 0.4785V / G =～0.79g
RZ = 0.16V / 0.4785V / G =～0.33g

当然，我们可以把所有的步骤全部放在一个式子里，但我想通过介绍每一个步骤以便让你了解怎么读取一个ADC值并将其转换为单位为g的矢量力的分量。
Rx = (AdcRx * Vref / 1023 – VzeroG) / Sensitivity (公式2)
Ry = (AdcRy * Vref / 1023 – VzeroG) / Sensitivity
Rz = (AdcRz * Vref / 1023 – VzeroG) / Sensitivity

现在我们得到了惯性力矢量的三个分量，如果设备除了重力外不受任何外力影响，那我们就可以认为这个方向就是重力矢量的方向。
如果你想计算设备相对于地面的倾角，可以计算这个矢量和Z轴之间的夹角。
如果你对每个轴的倾角都感兴趣，你可以把这个结果分为两个分量：X轴、Y轴倾角，这可以通过计算重力矢量和X、Y轴的夹角得到。
计算这些角度比你想象的简单，现在我们已经算出了Rx，Ry，Rz的值，让我们回到我们的上一个加速度模型，再加一些标注上去：

我们感兴趣的角度是向量R和X，Y，Z轴之间的夹角，那就令这些角度为Axr，Ayr，Azr。观察由R和Rx组成的直角三角形：
cos(Axr) = Rx / R , 类似的：
cos(Ayr) = Ry / R
cos(Azr) = Rz / R
从公式1我们可以推导出 R = SQRT( Rx^2 + Ry^2 + Rz^2)
通过arccos()函数（cos()的反函数）我们可以计算出所需的角度：
Axr = arccos(Rx/R)
Ayr = arccos(Ry/R)
Azr = arccos(Rz/R)

我们花了大段的篇幅来解释加速度计模型，最后所要的只是以上这几个公式。
根据你的应用场合，你可能会用到我们推导出来的几个过渡公式。

加速度传感器可以用来测量加速度，或者检测倾斜、冲击、振动等运动状态，
帮助实现工业、医疗、通信、消费电子和汽车等领域中的多种应用。
根据不同的应用，加速度传感器的测量范围从几g 到几十g 不等。
数字输出的加速度传感器还会集成多种中断模式。
这些特性可以为用户提供更加方便灵活的解决方案。

陀螺仪：

接下来要介绍陀螺仪模块。
但在此之前，我们再介绍几个很常用的公式：
cosX = cos(Axr) = Rx / R
cosY = cos(Ayr) = Ry / R
cosZ = cos(Azr) = Rz / R
这三个公式通常称作方向余弦 ，它主要表达了单位向量（长度为1的向量）和R向量具有相同的方向。
你可以很容易地验证：
SQRT（cosX ^ 2 + COSY ^ 2 + cosZ ^ 2）= 1
这是个很好的性质，因为它避免了我们一直检测R向量的模（长度）。
通常如果我们只是对惯性力的方向感兴趣，那标准化模长以简化其他计算是个明智的选择。

陀螺仪的每个通道检测一个轴的旋转。
例如，一个2轴陀螺仪检测绕X和Y轴的旋转。
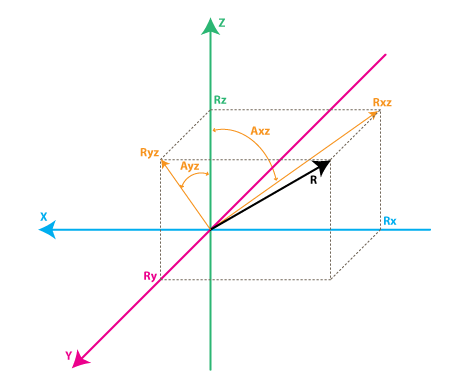
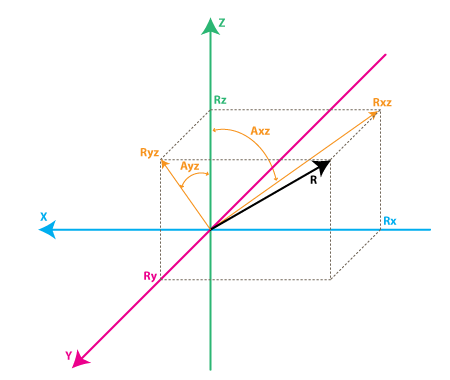
为了用数字来表达这些旋转，我们先引进一些符号。首先我们定义：
Rxz – 惯性力矢量R在XZ平面上的投影
Ryz – 惯性力矢量R在YZ平面的上投影
在由Rxz和Rz组成的直角三角形中，运用勾股定理可得：
Rxz^2 = Rx^2 + Rz^2 ，同样：
Ryz^2 = Ry^2 + Rz^2
同时注意：
R^2 = Rxz^2 + Ry^2 ，这个公式可以公式1和上面的公式推导出来，也可由R和Ryz所组成的直角三角形推导出来
R ^ 2 = Ryz ^ 2 + RX ^ 2


相反，我们按如下方法定义Z轴和Rxz、Ryz向量所成的夹角：
AXZ - Rxz（矢量R在XZ平面的投影）和Z轴所成的夹角
AYZ - Ryz（矢量R在YZ平面的投影）和Z轴所成夹角


陀螺仪测量上面定义的角度的变化率。
换句话说，它会输出一个与上面这些角度变化率线性相关的值。
为了解释这一点，我们先假设在t0时刻，我们已测得绕Y轴旋转的角度（也就是Axz），定义为Axz0，之后在t1时刻我们再次测量这个角度，得到Axz1。
角度变化率按下面方法计算：
RateAxz = (Axz1 – Axz0) / (t1 – t0).
如果用度来表示角度，秒来表示时间，那这个值的单位就是 度/秒。这就是陀螺仪检测的东西。
在实际运用中，陀螺仪一般都不会直接给你一个单位为度/秒的值（除非它是个特殊的数字陀螺仪）。


得到一个ADC值并且要用类似公式2的式子将其转换成单位为 度/秒的值。
让我们来介绍陀螺仪输出值转换中的ADC部分（假设使用10位ADC模块，如果是8位ADC，用1023代替255，如果是12为ADC用4095代替1023）。
RateAxz = (AdcGyroXZ * Vref / 1023 – VzeroRate) / Sensitivity 公式3
RateAyz = (AdcGyroYZ * Vref / 1023 – VzeroRate) / Sensitivity
AdcGyroXZ，AdcGyroYZ - 这两个值由ADC读取，它们分别代表矢量R的投影在XZ和YZ平面内里的转角，也可等价的说，旋转可分解为单独绕Y和X轴的运动。
Vref – ADC的参考电压，上例中我们使用3.3V
VzeroRate – 是零变化率电压，换句话说它是陀螺仪不受任何转动影响时的输出值，对Acc Gyro板来说，可以认为是1.23V（此值通常可以在说明书中找到——但千万别相信这个值，因为大多数的陀螺仪在焊接后会有一定的偏差，所以可以使用电压计测量每个通道的输出值，通常这个值在焊接后就不会改变，如果有跳动，在设备使用前写一个校准程序对其进行测量，用户应当在设备启动的时候保持设备静止以进行校准）。
Sensitivity –陀螺仪的灵敏度，单位mV/(deg/s)，通常写作mV/deg/s,它的意思就是如果旋转速度增加1°/s,陀螺仪的输出就会增加多少mV。Acc_Gyro板的灵敏度值是2mV/deg/s或0.002V/deg/s


让我们举个例子，假设我们的ADC模块返回以下值：
AdcGyroXZ = 571
AdcGyroXZ = 323
用上面的公式，在代入Acc Gyro板的参数，可得：
RateAxz = (571 * 3.3V / 1023 – 1.23V) / ( 0.002V/deg/s) =~ 306 deg/s
RateAyz = (323 * 3.3V / 1023 – 1.23V) / ( 0.002V/deg/s) =~ -94 deg/s
换句话说设备绕Y轴（也可以说在XZ平面内）以306°/s速度和绕X轴（或者说YZ平面内）以-94°/s的速度旋转。
请注意，负号表示该设备朝着反方向旋转。按照惯例，一个方向的旋转是正值。一份好的陀螺仪说明书会告诉你哪个方向是正的，否则你就要自己测试出哪个旋转方向会使得输出脚电压增加。最好使用示波器进行测试，因为一旦你停止了旋转，电压就会掉回零速率水平。如果你使用的是万用表，你得保持一定的旋转速度几秒钟并同时比较电压值和零速率电压值。如果值大于零速率电压值那说明这个旋转方向是正向。

加速度计和陀螺仪的数据融合算法：

注：具体的代码实现和算法测试，请阅读这篇文章： http://starlino.com/imu_kalman_arduino.html

融合加速度计和陀螺仪时，首先要做的就是统一它们的坐标系。
最简单的办法就是将加速度计作为参考坐标系。
大多数的加速度计规格书都会指出对应于物理芯片或设备的XZY轴方向。
例如，下面就是Acc Gyro板的说明书中给出的XYZ轴方向：

接下来的步骤是：
- 确定陀螺仪的输出对应到上述讨论的RateAxz，RateAyz值。
- 根据陀螺仪和加速度计的位置决定是否要反转输出值


不要设想陀螺仪陀的输出有XY，它会适应加速度计坐标系里的任何轴，尽管这个输出是IMU模块的一部分。最好的办法就是测试。


接下来的示例用来确定哪个陀螺仪的输出对应RateAxz。
- 首先将设备保持水平。加速度计的XY轴输出会是零加速度电压（Acc Gyro板的值是1.65V）
- 接下来将设备绕Y轴旋转，换句话说就是将设备在XZ平面内旋转，所以X、Z的加速度输出值会变化而Y轴保持不变。
- 当以匀速旋转设备的时候，注意陀螺仪的哪个通道输出值变化了，其他输出应该保持不变。
- 在陀螺仪绕Y轴旋转（在XZ平面内旋转）的时候输出值变化的就是AdcGyroXZ，用于计算RateAxz
- 最后一步，确认旋转的方向是否和我们的模型对应，因为陀螺仪和加速度的位置关系，有时候你可能要把RateAxz值反向
- 重复上面的测试，将设备绕Y轴旋转，这次查看加速度计的X轴输出（也就是AdcRx）。如果AdcRx增大（从水平位置开始旋转的第一个90°），那AdcGyroXZ应当减小。这是因为我们观察的是重力矢量，当设备朝一个方向旋转时矢量会朝相反的方向旋转（相对坐标系运动）。
所以，如果你不想反转RateAxz，你可以在公式3中引入正负号来解决这个问题：
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 – VzeroRate) / Sensitivity ,其中InvertAxz= 1 或-1
同样的方法可以用来测试RateAyz，将设备绕X轴旋转，你就能测出陀螺仪的哪个输出对应于RateAyz，以及它是否需要反转。
一旦你确定了InvertAyz，你就能可以用下面的公式来计算RateAyz：
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 – VzeroRate) / Sensitivity


如果对Acc Gyro板进行这些测试，你会得到下面的这些结果：
- RateAxz的输出管脚是GX4，InvertAxz = 1
- RateAyz输出管脚是GY4，InvertAyz = 1
从现在开始我们认为你已经设置好了IMU模块并能计算出正确的Axr，Ayr，Azr值（在第一部分加速度计中定义）以及RateAyz，RateAyz（在第二部分陀螺仪中）。


下一步，我们分析这些值之间的关系并得到更准确的设备和地平面之间的倾角。
你可能会问自己一个问题，如果加速度计已经告诉我们Axr，Ayr，Azr的倾角，为什么还要费事去得到陀螺仪的数据？答案很简单：加速度计的数据不是100%准确的。
还有几个原因，还记加速度计测量的是惯性力，这个力可以由重力引起（理想情况只受重力影响），当也可能由设备的加速度（运动）引起。
因此，就算加速度计处于一个相对比较平稳的状态，它对一般的震动和机械噪声很敏感。这就是为什么大部分的IMU系统都需要陀螺仪来使加速度计的输出更平滑。
但是怎么办到这点呢？陀螺仪不受噪声影响吗？
陀螺仪也会有噪声，但由于它检测的是旋转，因此对线性机械运动没那么敏感，不过陀螺仪有另外一种问题，比如漂移（当选择停止的时候电压不会回到零速率电压）。
然而，通过计算加速度计和陀螺仪的平均值我们能得到一个相对更准确的当前设备的倾角值，这比单独使用加速度计更好。

误差或错误数据的卡尔曼滤波算法：

我们要介绍一种算法，算法受卡尔曼滤波中的一些思想启发，但是它更简单并且更容易在嵌入式设备中实现。
在此之前，让我们先看看我们需要算法计算什么值。
所要算的就是重力矢量R=[Rx,Ry,Rz]，它可由其他值推导出来，如Axr，Ayr，Azr或者cosX，cosY，cosZ，由这些值我们能得到设备相对地平面的倾角值，这些关系我们在第一部分已经讨论过。
有人可能会说-根据第一部分的公式2我们不是已经得到Rx，Ry，Rz的值了吗？


是的，但是这些值只是由加速度计数据推导出来的，如果你直接将它们用于你的程序你会得到难以忍受的噪声。
为了避免进一步的混乱，我们重新定义加速度计的测量值：
Racc – 是由加速度计测量到得惯性力矢量，它可分解为下面的分量（在XYZ轴上的投影）：
RxAcc = (AdcRx * Vref / 1023 – VzeroG) / Sensitivity
RyAcc = (AdcRy * Vref / 1023 – VzeroG) / Sensitivity
RzAcc = (AdcRz * Vref / 1023 – VzeroG) / Sensitivity
现在我们得到了一组只来自于加速度计ADC的值。
我们把这组数据叫做“vector”，并使用下面的符号：
Racc = [RxAcc,RyAcc,RzAcc]
因为这些Racc的分量可由加速度计数据得到，我们可以把它当做算法的输入。
请注意Racc测量的是重力，如果你得到的矢量长度约等于1g那么你就是正确的：
|Racc| = SQRT(RxAcc^2 +RyAcc^2 + RzAcc^2),
但是请确定把矢量转换成下面的矢量非常重要：
Racc(normalized) = [RxAcc/|Racc| , RyAcc/|Racc| , RzAcc/|Racc|].
这可以确保标准化Racc始终是1。


接来下引进一个新的向量：
Rest = [RxEst,RyEst,RzEst]
这就是算法的输出值，它经过陀螺仪数据的修正和基于上一次估算的值。


这是算法所做的事：
-加速度计告诉我们：“你现在的位置是Racc”
         我们回答：“谢谢，但让我确认一下”
-然后根据陀螺仪的数据和上一次的Rest值修正这个值并输出新的估算值Rest。
-我们认为Rest是当前设备姿态的“最佳值”。


让我们看看它是怎么实现的。
数列的开始，我们先认为加速度值正确并赋值：
Rest(0) = Racc(0)
Rest和Racc是向量，所以上面的式子可以用3个简单的式子代替，注意别重复了：
RxEst（0）= RxAcc（0）
RyEst（0）= RyAcc（0）
RzEst（0）= RzAcc（0）


接下来我们在每个等时间间隔T秒做一次测量，得到新的测量值，并定义为Racc（1），Racc（2），Racc（3）等等。
同时，在每个时间间隔我们也计算出新的估算值Rest（1）,Rest（2），Rest（3），等等。


假设我们在第n步。我们有两列已知的值可以用：
Rest(n-1) – 前一个估算值，Rest(0) = Racc(0)
Racc(n) – 当前加速度计测量值
在计算Rest（n）前，我们先引进一个新的值，它可由陀螺仪和前一个估算值得到。
叫做Rgyro，同样它是个矢量并由3个分量组成：
Rgyro = [RxGyro,RyGyro,RzGyro]
我们分别计算这个矢量的分量，从RxGyro开始。

首先观察陀螺仪模型中下面的关系，根据由Rz和Rxz组成的直角三角形我们能推出：
tan(Axz) = Rx/Rz => Axz = atan2(Rx,Rz)
你可能从未用过atan2这个函数，它和atan类似，但atan返回值范围是（-PI/2,PI/2），atan2返回值范围是（-PI，PI），并且他有两个参数。
它能将Rx，Rz值转换成360°（-PI，PI）内的角度。更多信息请阅读 atan2.
所以，知道了RxEst（n-1）和RzEst（n-1）我们发现：
Axz(n-1) = atan2( RxEst(n-1) , RzEst(n-1) ).


陀螺仪测量的是Axz角度变化率，因此，我们可以按如下方法估算新的角度Axz（n）：
Axz(n) = Axz(n-1) + RateAxz(n) * T
RateAxz可由陀螺仪ADC读取得到。
通过使用平均转速可由得到一个更准确的公式：
RateAxzAvg =（RateAxz（N）+ RateAxz（N-1））/ 2
Axz(n) = Axz(n-1) + RateAxzAvg * T
同理可得：
Ayz(n) = Ayz(n-1) + RateAyz(n) * T
好了，我们有了Axz（n），Ayz（n）。


现在我们如何推导出RxGyro/RyGyro?
根据公式1我们可以把Rgyro长度写成下式：
| Rgyro | = SQRT（RxGyro ^ 2 + RyGyro ^ 2 + RzGyro ^ 2）
同时，因为我们已经将Racc标准化，我们可以认为它的长度是1并且旋转后保持不变，所以写成下面的方式相对比较安全：
| Rgyro | = 1
我们暂时采用更短的符号进行下面的计算：
x =RxGyro , y=RyGyro, z=RzGyro
根据上面的关系可得：
x = x / 1 = x / SQRT(x^2+y^2+z^2)
分子分母同除以SQRT（X ^ 2 + Z ^ 2）
x = ( x / SQRT(x^2 + z^2) ) / SQRT( (x^2 + y^2 + z^2) / (x^2 + z^2) )
注意x / SQRT(x^2 + z^2) = sin(Axz), 所以:
x = sin(Axz) / SQRT (1 + y^2 / (x^2 + z^2) )
将SQRT内部分式的分子分母同乘以z^2
x = sin(Axz) / SQRT (1 + y^2  * z ^2 / (z^2 * (x^2 + z^2)) )
注意 z / SQRT(x^2 + z^2) = cos(Axz)， y / z = tan(Ayz), 所以最后可得:
x = sin(Axz) / SQRT (1 + cos(Axz)^2 * tan(Ayz)^2 )
替换成原来的符号可得：
RxGyro = sin(Axz(n)) / SQRT (1 + cos(Axz(n))^2 * tan(Ayz(n))^2 )
同理可得：
RyGyro = sin(Ayz(n)) / SQRT (1 + cos(Ayz(n))^2 * tan(Axz(n))^2 )


提示：这个公式还可以更进一步简化。分式两边同除以sin（axz（你））可得：
RxGyro =  1  / SQRT (1/ sin(Axz(n))^2  + cos(Axz(n))^2 / sin(Axz(n))^2  * tan(Ayz(n))^2 )
RxGyro =  1  / SQRT (1/ sin(Axz(n))^2  + cot(Axz(n))^2  * sin(Ayz(n))^2  / cos(Ayz(n))^2 )  
现在加减   cos(Axz(n))^2/sin(Axz(n))^2   = cot(Axz(n))^2 
RxGyro =  1  / SQRT (1/ sin(Axz(n))^2  -  cos(Axz(n))^2/sin(Axz(n))^2   + cot(Axz(n))^2  * sin(Ayz(n))^2  / cos(Ayz(n))^2  + cot(Axz(n))^2 )
综合条件1、2和3、4可得：
RxGyro =  1  / SQRT (1  +   cot(Axz(n))^2 * sec(Ayz(n))^2 ),     其中  cot(x) = 1 / tan(x)  ， sec(x) = 1 / cos(x)
这个公式只用了2个三角函数并且计算量更低。
如果你有Mathematica程序，通过使用 FullSimplify [Sin[A]^2/ ( 1 + Cos[A]^2 * Tan[B]^2)]你可以验证这个公式。




现在我们发现：
RzGyro  =  Sign(RzGyro)*SQRT(1 – RxGyro^2 – RyGyro^2).
其中，当 RzGyro>=0时，Sign(RzGyro) = 1 , 当 RzGyro<0时，Sign(RzGyro) = -1 。


一个简单的估算方法：
Sign(RzGyro) = Sign(RzEst(n-1))
在实际应用中，当心RzEst（n-1）趋近于0。
这时候你可以跳过整个陀螺仪阶段并赋值：Rgyro=Rest（n-1）。Rz可以用作计算Axz和Ayz倾角的参考，当它趋近于0时，它可能会溢出并引发不好的后果。
这时你会得到很大的浮点数据，并且tan()/atan()函数得到的结果会缺乏精度。


现在我们回顾一下已经得到的结果，我们在算法中的第n步，并计算出了下面的值：
Racc – 加速度计读取的当前值
Rgyro –根据Rest(-1)和当前陀螺仪读取值所得


我们根据哪个值来更新Rest（n）呢？你可能已经猜到，两者都采用。我们会用一个加权平均值，得：
Rest(n) = (Racc * w1 + Rgyro * w2 ) / (w1 + w2)
分子分母同除以w1，公式可简化成：
Rest(n) = (Racc * w1/w1 + Rgyro * w2/w1 ) / (w1/w1 + w2/w1)
令w2=w1=wGyro，可得：
Rest(n) = (Racc + Rgyro * wGyro ) / (1 + wGyro)
在上面的公式中，wGyro表示我们对加速度计和陀螺仪的相信程度。
这个值可以通过测试确定，根据经验值5-20之间会得到一个很好的结果。


此算法和卡尔曼滤波最主要的差别是它的权重是相对固定的，而卡尔曼滤波中的权重会随着加速度计读取的噪声而改变。
卡尔曼滤波注重给你一个“最好”的理论结果，而此算法给你的是实际项目中“够用”的结果。
你可以实现一个算法，它能根据测量的噪声而改变wGyro值，但对大部分应用来说固定的权重也能工作的很好。


现在得到最新的估算值还差一步：
RxEst(n) = (RxAcc + RxGyro * wGyro ) / (1 + wGyro)
RyEst(n) = (RyAcc + RyGyro * wGyro ) / (1 + wGyro)
RzEst(n) = (RzAcc + RzGyro * wGyro ) / (1 + wGyro)
现在，再次标准化矢量：
R = SQRT(RxEst(n) ^2 + RyEst(n)^2 +  RzEst(n)^2 )
RxEst(n) = RxEst(n)/R
RyEst(n) = RyEst(n)/R
RzEst(n) = RzEst(n)/R
现在，可以再次进行下一轮循环了。


注：关于此算法的具体实现和测试，请阅读这篇文章：
http://starlino.com/imu_kalman_arduino.html


加速度计和陀螺仪IMU融合的其他资源：
http://www.mikroquad.com/pub/Res ... ryFilter/filter.pdf
http://stackoverflow.com/questio ... -accelerometer-data
http://www.dimensionengineering.com/accelerometers.htm

2016年2月17日

传感器的使用与滤波算法（数据处理）的关系

误差或错误数据的来源

^1[2013]直立位置的角度值和在倒下去或倾斜的时候的快慢值（角速度），其实他们是一个量，因为对角速度积分就是角度值。

角速度只是反映了倒下去或倾斜的快慢，即变化量。

好比你拿一根筷子直立在手指上，你看见它要倒下去的时候，手肯定会跟着移动；

你一方面看到的是筷子倒下去的角度，另一个是筷子倒的时候的快慢，角度大速度快，你自然移动地快、幅度也大，角度小、速度慢，你自然移动的慢幅度也小。

测量角度一般使用加速度计就可以了，加速度计是分为模拟的和数字的两种，都是可以使用的。

在实际情况中，加速度计测量的角度是不准确的，因为在运动过程中存在震动加速度，这会使输出值不准确，不能真实反映偏转角度。

这是电子元器件本身的问题，有些人说用简单的数字滤波（中值、均值等），这些滤波滤除的是干扰信号，这信号本身的错误怎么滤除？

再来考虑另一个器件陀螺仪，我们知道陀螺仪是测量角速度的，但是角速度换算成角度是需要一个积分过程，假如在输入时有一个极小的误差，那么这个误差随着积分将会越来越大，最后得出的角度自然也是不准确的。（元器件的使用是最基本知识，需要把这两个传感器的使用先搞明白，明白角度具体是怎么计算出来的？）

滤波算法（数据处理）

这个时候才有我们常说的卡尔曼滤波、互补滤波的登场，很多人在设计过程中总是觉得卡尔曼或者互补滤波是很高端的东西，视线全被它们蒙蔽了，实际上它们最终的目的仍然是得到最准确的角度偏离值。对于这一目标，传感器的性能、电路设计同样很重要的。

其实作为应用，我们只需知道“卡尔曼滤波”输入的两个量，一个是测量值，一个是预测值，程序都是成型的，重点是在参数的调试上。整个算法中影响输出的就是Kg的值，可以简单的理解为一种加权行为，相信谁更多一点而已。整个调试过程有三个参数需要调整，Q  R  及那个0.0235 。具体的调试，目前还说不清楚，往往算法的调试都是经验，尝试多了就有规律了，需要再把这种经验给理论化简单描述出来。

 

代码如下：

说明：简化版卡尔曼滤波

volatile float QingJiao = 0;  //最终准确角度输出变量定义

volatile float Gyro_Data = 0; //陀螺仪

float Q =1, R =3900;    //调整卡尔曼的滞后 3900 

static float RealData = 0,RealData_P =10000;

float NowData = 0,NowData_P =0 ;

float Kg = 0,gyroscope_rate = 0,gyroscope_rat = 0,accelerometer_angle;

volatile float gyroscope_angle=0     ;                                                //用卡尔曼滤波时不用此变量

int  Gyro1_zero=0;

void kalman_update(void)

{

   if(zeroflag>1000)   //与开机自检有关，没用到的可以删去     

  {zeroflag=1001;  //确保zeroflag不会溢出

//-------------------------------------------------------------------------------------------------------------------------------

   Acc_z = Acc_z - 28850;      //加速度计采集的AD值减去直立时的输出值

  

   Gyro1_zero=zerosub/1000;   //陀螺仪开机自检累加1000次后取均值 得到陀螺仪零偏值

   Gyro1  = Gyro1 - Gyro1_zero;  //陀螺仪AD采集值减去陀螺仪零偏值        

   Gyro_Data = Gyro1; 

   accelerometer_angle=    Acc_z*180/(47915.71-12843.7);    //加速度计计算出的角度 归一化到-90 到+90

   gyroscope_rate = Gyro1*0.0235*0.005;  //0.0235 是转换角度的比例值 0.005是控制周期

   gyroscope_rat =gyroscope_rat-Gyro1*0.0235*0.005;     //积分角速度得到角度

//卡尔曼五个公式的算法实现                                                                             

    NowData = RealData-gyroscope_rate;

    NowData_P = Q+RealData_P;

    Kg = NowData_P/(NowData_P+R);

    RealData = NowData +Kg*(accelerometer_angle - NowData);

    RealData_P =(1-Kg)*NowData_P;

      QingJiao =  RealData;   //将准确角度结果给QingJiao

      }

}

 

假如已经得到准确角度，自然是开始以此作为控制量，那我们要控制成啥样？想一想也知道是要把这个角度值控制成0度（例如：将直立时定义为0度），那么自然使用常用的PID算法，偏差自然就是QingJiao-0=QingJiao，当然也可以反过来，这根据自己对方向的定义。我们来个最简单的位置式PD算法：

fValue = (float) P *QingJiao -(float) D*Gyro_Data;    

P就是PID的P参数 D就是PID的D参数，QingJiao反映幅度，Gyro_Data反映快慢。（这也需要不断调试出来的。）再把fvalue值给平衡车的直流电机的控制调速PWM输出就可以了。

实际在做的时候，往往没那么简单，所以一定要一步一步做好之后再做后面的，假如你第二部没做好，在第三部时你怎么也直立不起来，你不知道到底是PD参数不对，还是卡尔曼出来的角度本身不准。所以个人经验：得到准确角度是整个过程至关重要的一步。平衡车的直立是一直是一个动态过程，即使最好的状态一动不动，也是在动态控制中，只是看不出而已。这里只针对直立控制，即最基本的自平衡。

参考：

加速度计和陀螺仪指南    http://www.geek-workshop.com/thread-1695-1-1.html

A Guide To using IMU (Accelerometer and Gyroscope Devices) in Embedded Applications.               Posted on: December 29, 2009 by starlino   

http://www.starlino.com/imu_guide.html

6轴和9轴传感器：惯性测量单元 和 航姿参考系统

IMU(Inertial measurement unit )和AHRS (Attitude and heading reference system)

2016年2月19日

在研究技术问题之前，我并不关心这些传感器的细节，但要上新的产品、需要更新的技术的时候，市场上找人不是一件容易的事情。

与其等工程师都会的时候，可能你的产品也没什么竞争力了。无奈，自己跟着参与吧。

就算少数人会使用新技术，你也需要有足够的人际技巧，其实不能说是技巧，应该是一套方法论来团结你的盟友，比如共同的理想（对未来的预见）、协调一致的目标、价值观及一致行动准则。这些远远要比编程设计复杂，有时候我在想马云真的是非常厉害的人物，能团结18罗汉在相当长的时间里，听他的”鬼话“，被他”忽悠“，这是需要怎样的一套方法呢！想想当下，如果你要团结一批人，是非常不容易的。

言归正传，不管什么IMU或AHRS对我来说都是传感器数量和结构的问题，但要采用前人的成果，就得大家说一样的话，就是这些专业术语。

AHRS由加速度计，磁场计，陀螺仪构成
AHRS的输出中的绝对方向来自于地球的重力场和地球的磁场，尤其是磁场
静态终精度取决于对磁场的测量精度和对重力的测量精度 ,而则陀螺决定了他的动态性能。

磁场和重力场越正交，则航姿测量效果越好；反之，如果磁场和重力场平行了，比如在地磁南北极，这里的磁场是向下的，即和重量场方向相同了。
这时航向角是没法测出的，这是航姿系统的缺陷。在高纬度的地方航线角误差会越来越大。当然，在实际非航天级的应用中很少遇到这种情况，故此段只是为了”知其所以然“可略去。

消费级陀螺仪和加速度计的噪声相对来说很大，
以平面陀螺为例用ADI的陀螺仪进行积分一分钟会漂移2度左右，这种前提下如果没有磁场和重力场来校正三轴陀螺的话，
那么基本上3分钟以后物体的实际姿态和测量输出姿态就完全变样了，所以，低价陀螺仪和加速度计的架构下必须运用场向量来进行修正。

AHRS利用三维的陀螺仪来快速跟踪被测物体的三维的姿态，它以陀螺仪为核心，同时也测量加速度和地磁场的方向为系统提供可靠的参考。

具体测量载体三个方向的的绝对角速率、加速度以及磁场强度，并采用特定姿态解算方法和卡尔曼滤波信息融合得到载体的四元数、姿态数据等。

需要实时的集成算法为系统提供准确，可靠，及时以及稳定的姿态输出。

从陀螺仪、加速度计、磁力计以及内部温度传感器得到的数据，全部被传输到嵌入式系统-MCU中。
MCU依据特定的算法以及存储在Flash存储器中的标定数据处理来自传感器的原始数据，
作为其基本算法，航姿参考系统（AHRS）采用自适应卡尔曼滤波算法，自动调整并适应不断变化的动态条件，无需外部人为的干预。
产品均在特定的环境实验条件下，参考已知温度下的加速度、角速率和磁场进行全面的标定，并将标定数据输入每个产品中。

产品应用：
船舶测控、工程机械、车辆、通讯天线和雷达、平台稳定系统、
机器人控制、无人机/直升机、虚拟现实、游戏、动画、体育、医疗康复等。

参考文献：

四元数与欧拉角之间的转换    http://blog.csdn.net/yaokang522/article/details/46789075

请教四轴AHRS算法的问题        http://www.openedv.com/posts/list/49740.htm

STM32可以用的卡尔曼滤波，附带AHRS姿态解算源码      http://bbs.elecfans.com/jishu_487795_1_1.html

AHRS--APM飞控基于DCM算法的姿态及航向解算核心代码     http://www.docin.com/p-880458906.html

AHRS 姿态板首试     http://www.amobbs.com/thread-5468886-5-1.html

The Extended Kalman Filter: An Interactive Tutorial for Non-Experts      http://home.wlu.edu/~levys/kalman_tutorial/

捷联惯导算法心得    http://www.amobbs.com/thread-5492189-1-1.html

9DOF姿态融合 四元数 欧拉角转换 有代码有内涵    http://www.amobbs.com/thread-5549022-1-1.html