devbox
菜鸟追梦旅行
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

数据结构-考研难点代码突破 (图关键路径完全解析（流程+代码） - C++代码)_考研求关键路径需要步骤吗

作者：菜鸟追梦旅行 | 2024-06-08 16:17:23

赞

踩

考研求关键路径需要步骤吗

考研在关键路径上的考察以流程为主

文章目录

1. AOE网

首先区分AOV网：
AOV网∶若用DAG 图（有向无环图）表示一个工程，其顶点表示活动，用有向边<Vi，Vj>表示活动 Vi必须先于活动Vj进行的这样一种关系，则将这种有向图称为顶点表示活动的网络，记为 AOV网。

AOE网：
在带权有向图中，以顶点表示事件，以有向边表示活动，以边上的权值表示完成该活动的开销（如完成活动所需的时间)，称之为用边表示活动的网络，简称AOE网

AOE网具有以下两个性质:

  1. 只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始
  2. 只有在进入某顶点的各有向边所代表的活动都已结束时，该顶点所代表的事件才能发生。（有些事件可以并行执行）

在AOE网中仅有一个入度为0的顶点，称为开始顶点（源点)，它表示整个工程的开始;
也仅有一个出度为0的顶点，称为结束顶点（汇点)，它表示整个工程的结束。

eg：
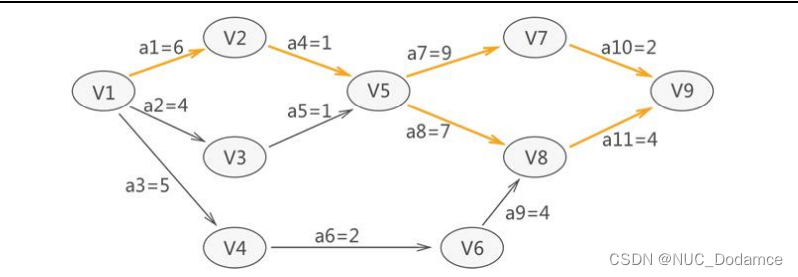
在这里插入图片描述
我们用有向无环网描述某项工程时，数据结构中称这样的网结构为AOE（Activity OnEdge）网，网中的顶点称为“事件”，弧称为“活动”，弧对应的权值代表活动持续的时间

关键路径：
从源点到汇点的有向路径可能有多条，所有路径中，具有最大路径长度的路径称为关键路径，而把关键路径上的活动称为关键活动

完成整个工程的最短时间就是关键路径的长度，若关键活动不能按时完成，则整个工程的完成时间就会延长

2. 关键路径问题解决流程

为了解决关键路径问题，需要引入一下参数：

  1. 事件v的最早发生时间ve：决定了所有从v开始的活动能够开工的最早时间

  2. 活动a的最早开始时间e：指该活动弧的起点所表示的时间最早发生的时间

  3. 事件v的最迟发生时间vl：它是指在不推迟整个工程完成的前提下，该事件最迟必须发生的时间。

  4. 活动a最迟开始时间l：活动弧的重点表示的事件最迟发生时间vl-该活动所需要的时间差。

  5. 活动的时间余量：活动最迟开始时间-最早开始时间，表示在不增加完成整个工程所需总时间的情况下，活动a可以拖延的时间

    如果活动的时间余量为0，称为关键活动。

求关键活动步骤：

  1. 求所有事件的最早发生时间ve()：

    按拓扑排序序列，依次求各个顶点的ve(k)：ve(源点)=0
    ve(k)= Max {ve(j)+Weight(v,vk)}，v为v的任意前驱
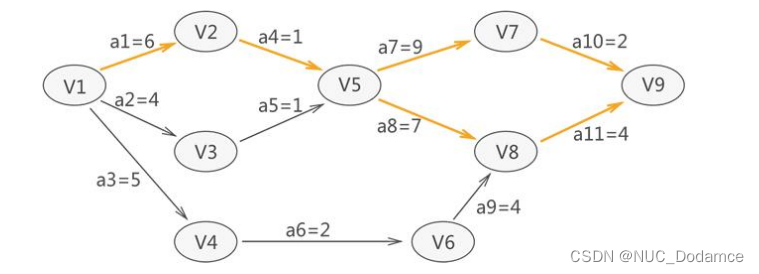
    在这里插入图片描述
    先求拓扑排序序列，按照拓扑排序序列计算事件最早发生时间ve(k)
    拓扑排序：1，2，3，4，5，6，7，8，9

    ve1=0，ve2=6，ve3=4，ve4=5，ve5=max(7,5)=7，ve6=7，ve7=16，ve8=14，v9=18

  2. 求所有事件的最迟发生时间vl()

    按逆拓扑排序序列，依次求各个顶点的vl(k)：vl(汇点)= ve(汇点)
    vl(k)= Min{vl(j) - Weight(vi,vj)}, v为v的任意后继

    汇点最迟发生时间和最早发生时间相同

    在这里插入图片描述
    逆拓扑序列：9，8，7，6，5，4，3，2，1

    vl9=ve9=18，vl8=14，vl7=16，vl6=10，vl5=min(7,7)=7，vl4=8，vl3=6，vl2=6，vl1=min(0，2，3)=0

  3. 求所有活动的最早发生时间e()

    若边<vk,vj>表示活动ai，则有e(i)= ve(k)

    在这里插入图片描述
    e1=0，e2=0，e3=0，e4=6，e5=4，e6=5，e7=7，e8=7，e9=7，e10=16，e11=14

a5活动最早发生时间就是这个弧的弧尾v3时间最早发生时间

  1. 求所有活动的最迟发生时间I()：

    若边<vk,vj>表示活动ai，则有l(i)= vl(j) - Weight(vk, v))

在这里插入图片描述
l11=14，l10=16，l9=10，l8=7，l7=7，l6=8，l5=6，l4=6，l3=3，l2=2，l1=0

a11活动最晚发生时间为<v7,v9>v9最晚发生时间-活动时间4（18-4=14）

  1. 求所有活动的时间余量d()，d(i)=0的活动就是关键活动，由关键活动可得关键路径

    最晚活动时间-最早活动时间d(i)= l(i)-e(i)

在这里插入图片描述
d1=0，d2=2-0，d3=3-0，d4=6-6=0，d5=6-4，d6=8-5，d7=7-7=0，d8=7-7=0，d9=10-7，d10=10-10=0，d11=14-14=0

根据上图分析，关键活动为:a1，a4，a7，a8，a10，a11

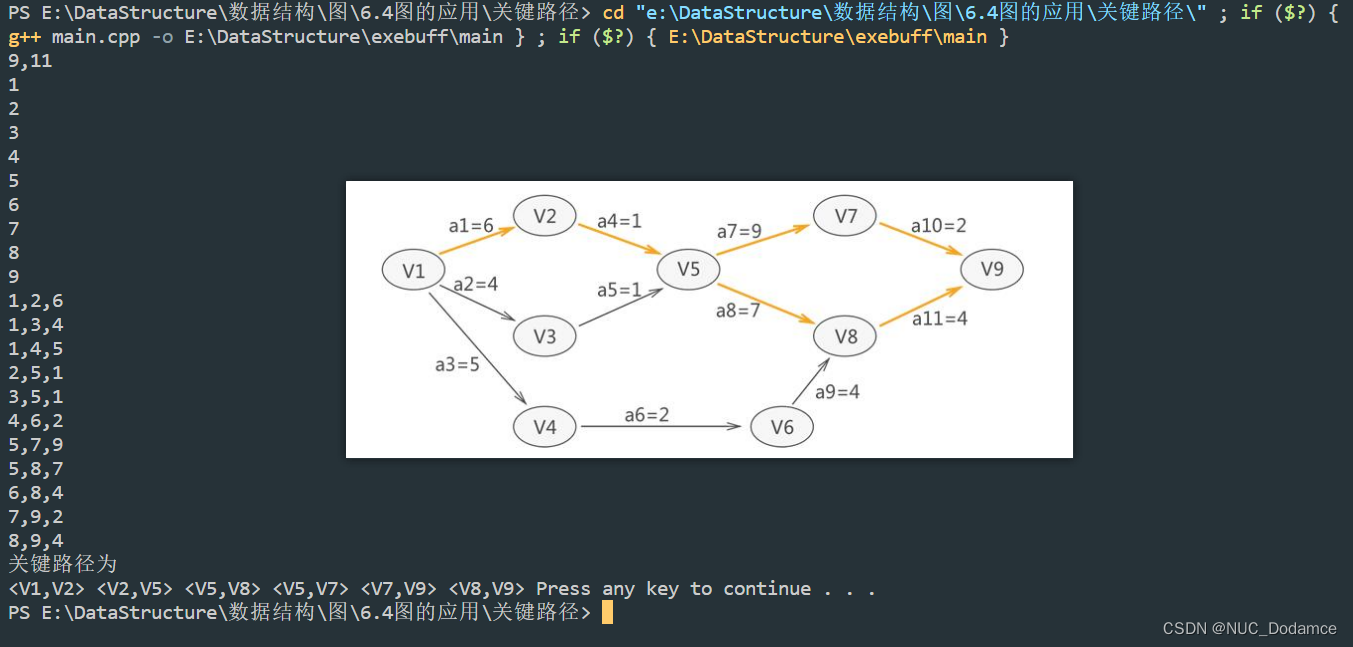
关键路径为：
<V1,V2> <V2,V5> <V5,V8> <V5,V7> <V7,V9> <V8,V9>

需要注意：

  1. 若关键活动耗时增加则整个工程的工期将增长
  2. 缩短关键活动的时间，可以缩短整个工程的工期
  3. 当缩短到一定程度时，关键活动可能会变成非关键活动
  4. 可能有多条关键路径，只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期，只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。（上图表示为加速a1，a4执行速度来缩短工程时间）

C++代码

#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTEX_NUM 20 // 最大顶点个数
#define VertexType int    // 顶点数据的类型

// 建立全局变量，存储各个顶点（事件）的最早发生时间
VertexType ve[MAX_VERTEX_NUM] = {0};
// 建立全局变量，保存各个顶点（事件）的最晚发生时间
VertexType vl[MAX_VERTEX_NUM] = {0};

typedef struct ArcNode
{
    int adjvex;              // 邻接点在数组中的位置下标
    struct ArcNode *nextarc; // 指向下一个邻接点的指针
    VertexType dut;
} ArcNode;

typedef struct VNode
{
    VertexType data;              // 顶点的数据域
    ArcNode *firstarc;            // 指向邻接点的指针
} VNode, AdjList[MAX_VERTEX_NUM]; // 存储各链表头结点的数组

typedef struct
{
    AdjList vertices;   // 图中顶点及各邻接点数组
    int vexnum, arcnum; // 记录图中顶点数和弧数
} ALGraph;

// 找到顶点在邻接表数组中的位置下标
int LocateVex(ALGraph G, VertexType u)
{
    int i;
    for (i = 0; i < G.vexnum; i++)
    {
        if (G.vertices[i].data == u)
        {
            return i;
        }
    }
    return -1;
}

// 邻接表存储 AOE 网（有向无环网）
void CreateAOE(ALGraph *G)
{
    int i, locate;
    VertexType initial, end, dut;
    ArcNode *p = NULL;
    scanf("%d,%d", &(G->vexnum), &(G->arcnum));
    for (i = 0; i < G->vexnum; i++)
    {
        scanf("%d", &(G->vertices[i].data));
        G->vertices[i].firstarc = NULL;
    }
    for (i = 0; i < G->arcnum; i++)
    {
        scanf("%d,%d,%d", &initial, &end, &dut);
        p = (ArcNode *)malloc(sizeof(ArcNode));
        p->adjvex = LocateVex(*G, end);
        p->nextarc = NULL;
        p->dut = dut;
        locate = LocateVex(*G, initial);
        p->nextarc = G->vertices[locate].firstarc;
        G->vertices[locate].firstarc = p;
    }
}

// 结构体定义栈结构
typedef struct stack
{
    VertexType data;
    struct stack *next;
} stack;

// 初始化栈结构
void initStack(stack **S)
{
    (*S) = (stack *)malloc(sizeof(stack));
    (*S)->next = NULL;
}

// 判断栈是否为空
bool StackEmpty(stack S)
{
    if (S.next == NULL)
    {
        return true;
    }
    return false;
}

// 进栈，以头插法将新结点插入到链表中
void push(stack *S, VertexType u)
{
    stack *p = (stack *)malloc(sizeof(stack));
    p->data = u;
    p->next = NULL;
    p->next = S->next;
    S->next = p;
}

// 弹栈函数，删除链表首元结点的同时，释放该空间，并将该结点中的数据域通过地址传值给变量i;
void pop(stack *S, VertexType *i)
{
    stack *p = S->next;
    *i = p->data;
    S->next = S->next->next;
    free(p);
}

void deleStack(stack *S)
{
    stack *del = NULL;
    if (S->next)
    {
        del = S->next;
        S->next = del->next;
        free(del);
    }
    free(S);
}

// 创建一个全局指针，后续会指向一个链栈
stack *T = NULL;

// 统计各顶点的入度
void FindInDegree(ALGraph G, int indegree[])
{
    int i;
    // 遍历邻接表，根据各链表中数据域存储的各顶点位置下标，在indegree数组相应位置+1
    for (i = 0; i < G.vexnum; i++)
    {
        ArcNode *p = G.vertices[i].firstarc;
        while (p)
        {
            indegree[p->adjvex]++;
            p = p->nextarc;
        }
    }
}

bool TopologicalOrder(ALGraph G)
{
    int index, i, indegree[MAX_VERTEX_NUM] = {0}; // 创建记录各顶点入度的数组
    // 建立链栈
    stack *S = NULL;
    int count = 0;
    ArcNode *p = NULL;
    FindInDegree(G, indegree); // 统计各顶点的入度
    // 初始化栈
    initStack(&S);
    // 查找度为0的顶点，作为起始点
    for (i = 0; i < G.vexnum; i++)
    {
        if (!indegree[i])
        {
            push(S, i);
        }
    }
    // 栈为空为结束标志
    while (!StackEmpty(*S))
    {
        // 弹栈，并记录栈中保存的顶点所在邻接表数组中的位置
        pop(S, &index);
        // 压栈，为求各边的最晚开始时间做准备（实现拓扑排序的逆过程）
        push(T, index);
        ++count;
        // 依次查找跟该顶点相关联的顶点，将它们的入度减1，然后将入度为 0 的顶点入栈
        for (p = G.vertices[index].firstarc; p; p = p->nextarc)
        {
            VertexType k = p->adjvex;
            if (!(--indegree[k]))
            {
                // 顶点入度为0，入栈
                push(S, k);
            }
            // 如果 index 的最早发生时间加上边的权值比 k 的最早发生时间还长，就覆盖ve数组中对应位置的值，最终结束时，ve数组中存储的就是各顶点的最早发生时间。
            if (ve[index] + p->dut > ve[k])
            {
                ve[k] = ve[index] + p->dut;
            }
        }
    }
    deleStack(S);
    // 如果count值小于顶点数量，表明有向图有环
    if (count < G.vexnum)
    {
        printf("该图有回路");
        return false;
    }
    return true;
}

// 求各顶点的最晚发生时间并计算出各边的最早和最晚开始时间
void CriticalPath(ALGraph G)
{
    int i, j, k;
    ArcNode *p = NULL;
    if (!TopologicalOrder(G))
    {
        return;
    }
    for (i = 0; i < G.vexnum; i++)
    {
        vl[i] = ve[G.vexnum - 1];
    }
    // 计算各个顶点的最晚发生时间
    while (!StackEmpty(*T))
    {
        pop(T, &j);
        for (p = G.vertices[j].firstarc; p; p = p->nextarc)
        {
            k = p->adjvex;
            // 构建Vl数组，在初始化时，Vl数组中每个单元都是18，如果每个边的汇点-边的权值比源点值小，就保存更小的。
            if (vl[k] - p->dut < vl[j])
            {
                vl[j] = vl[k] - p->dut;
            }
        }
    }
    printf("关键路径为\n");
    // 结合 ve 和 vl 数组中存储的数据，可以计算出每条边的最早开始时间和最晚开始时间，进而判断各个边是否为关键路径
    for (j = 0; j < G.vexnum; j++)
    {
        int ee, el;
        for (p = G.vertices[j].firstarc; p; p = p->nextarc)
        {
            k = p->adjvex;
            // 求各边的最早开始时间e[i],等于ve数组中相应源点存储的值
            ee = ve[j];
            // 求各边的最晚开始时间l[i]，等于汇点在vl数组中存储的值减改边的权值
            el = vl[k] - p->dut;
            // 判断e[i]和l[i]是否相等，如果相等，该边就是关键活动，相应的用*标记；反之，边后边没标记
            if (ee == el)
            {
                printf("<V%d,V%d> ", j + 1, k + 1);
            }
        }
    }
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • 153
  • 154
  • 155
  • 156
  • 157
  • 158
  • 159
  • 160
  • 161
  • 162
  • 163
  • 164
  • 165
  • 166
  • 167
  • 168
  • 169
  • 170
  • 171
  • 172
  • 173
  • 174
  • 175
  • 176
  • 177
  • 178
  • 179
  • 180
  • 181
  • 182
  • 183
  • 184
  • 185
  • 186
  • 187
  • 188
  • 189
  • 190
  • 191
  • 192
  • 193
  • 194
  • 195
  • 196
  • 197
  • 198
  • 199
  • 200
  • 201
  • 202
  • 203
  • 204
  • 205
  • 206
  • 207
  • 208
  • 209
  • 210
  • 211
  • 212
  • 213
  • 214
  • 215
  • 216
  • 217
  • 218
  • 219
  • 220
  • 221
  • 222
  • 223
  • 224
  • 225
  • 226
  • 227
  • 228
  • 229
  • 230
  • 231
  • 232
  • 233
  • 234
  • 235
  • 236
  • 237
  • 238
  • 239
  • 240
  • 241
  • 242
#include "criticalpath.h"

int main()
{
    ALGraph G;
    CreateAOE(&G); // 创建AOE网
    initStack(&T);
    TopologicalOrder(G);
    CriticalPath(G);
    deleStack(T);
    system("pause");
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13

在这里插入图片描述

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/菜鸟追梦旅行/article/detail/690366
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号