编辑这个页面须要登录或更高权限!
- 您刚才的请求只有这个用户组的用户才能使用:自动确认用户
- 如果您还没有登录请登录后重试。编程那点事是一个开放式网站,修改本站大部分内容仅须要花10秒钟时间创建一个账户。 如果您已经登录,本页面可能是受保护的内容。如果您认为有修改的必要,请联系本站管理人员。
- 该页面已被锁定以防止编辑。
NumPy 位运算
NumPy 广播主要应用numpy在算术运算期间处理具有不同形状的数组。受某些约束的影响,较小的数组在较大的数组上“广播”,以便它们具有兼容的形状。
NumPy 操作通常在逐个元素的基础上在数组对上完成。在最简单的情况下,两个数组必须具有完全相同的形状,如下例所示:
>>> import numpy as np >>> a = np.array([1, 2, 3]) >>> b = np.array([2, 2, 2]) >>> a * b array([ 2, 4, 6])
当运算中的 2 个数组的形状不同时,numpy 将自动触发广播机制。如:
>>> import numpy as np >>> a = np.array([[ 0, 0, 0], [10,10,10], [20,20,20], [30,30,30]]) >>> b = np.array([1,2,3]) >>> print(a + b) [[ 1 2 3] [11 12 13] [21 22 23] [31 32 33]]
下面的图片展示了数组 b 如何通过广播来与数组 a 兼容。
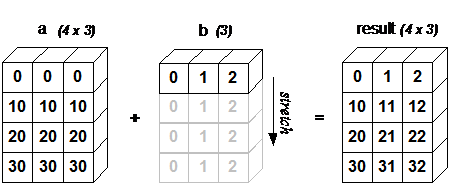
4x3 的二维数组与长为 3 的一维数组相加,等效于把数组 b 在二维上重复 4 次再运算:
>>> import numpy as np >>> a = np.array([[ 0, 0, 0], [10,10,10], [20,20,20], [30,30,30]]) >>> b = np.array([1,2,3]) >>> bb = np.tile(b, (4, 1)) # 重复 b 的各个维度 >>> print(a + bb) [[ 1 2 3] [11 12 13] [21 22 23] [31 32 33]]
一般广播规则
在两个数组上运行时,NumPy会逐元素地比较它们的形状。它从尾随尺寸开始,并向前发展。两个尺寸兼容时
他们是平等的,或者
其中一个是1
如果不满足这些条件,则抛出 ValueError: operands could not be broadcast together 异常,指示数组具有不兼容的形状。结果数组的大小是沿输入的每个轴不是1的大小。
数组不需要具有相同数量的维度。例如,如果您有一个256x256x3RGB值数组,并且希望将图像中的每种颜色缩放不同的值,则可以将图像乘以具有3个值的一维数组。根据广播规则排列这些数组的尾轴的大小,表明它们是兼容的:
Image (3d array): 256 x 256 x 3 Scale (1d array): 3 Result (3d array): 256 x 256 x 3
当比较的任何一个尺寸为1时,使用另一个尺寸。换句话说,尺寸为1的尺寸被拉伸或“复制”以匹配另一个尺寸。在以下示例中,A和B数组都具有长度为1的轴,在广播操作期间会扩展为更大的大小:
A (4d array): 8 x 1 x 6 x 1 B (3d array): 7 x 1 x 5 Result (4d array): 8 x 7 x 6 x 5
以下是一些实例:
A (2d array): 5 x 4 B (1d array): 1 Result (2d array): 5 x 4 A (2d array): 5 x 4 B (1d array): 4 Result (2d array): 5 x 4 A (3d array): 15 x 3 x 5 B (3d array): 15 x 1 x 5 Result (3d array): 15 x 3 x 5 A (3d array): 15 x 3 x 5 B (2d array): 3 x 5 Result (3d array): 15 x 3 x 5 A (3d array): 15 x 3 x 5 B (2d array): 3 x 1 Result (3d array): 15 x 3 x 5
以下是不广播的形状示例:
A (1d array): 3 B (1d array): 4 #尾部维度不匹配 A (2d array): 2 x 1 B (3d array): 8 x 4 x 3 #倒数第二个维度不匹配
实践中广播的一个实例:
>>> import numpy as np >>> x = np.arange(4) >>> xx = x.reshape(4,1) >>> y = np.ones(5) >>> z = np.ones((3,4)) >>> x.shape (4,) >>> y.shape (5,) >>> x + y ValueError: operands could not be broadcast together with shapes (4,) (5,) >>> xx.shape (4, 1) >>> y.shape (5,) >>> (xx + y).shape (4, 5) >>> xx + y array([[ 1., 1., 1., 1., 1.], [ 2., 2., 2., 2., 2.], [ 3., 3., 3., 3., 3.], [ 4., 4., 4., 4., 4.]]) >>> x.shape (4,) >>> z.shape (3, 4) >>> (x + z).shape (3, 4) >>> x + z array([[ 1., 2., 3., 4.], [ 1., 2., 3., 4.], [ 1., 2., 3., 4.]])
广播提供了一种方便的方式来获取两个数组的外积(或任何其他外部操作)。以下示例显示了两个1-d数组的外积操作:
>>> import numpy as np >>> a = np.array([0.0, 10.0, 20.0, 30.0]) >>> b = np.array([1.0, 2.0, 3.0]) >>> a[:, np.newaxis] + b array([[ 1., 2., 3.], [ 11., 12., 13.], [ 21., 22., 23.], [ 31., 32., 33.]])
这里 newaxis索引操作符插入一个新轴 a ,使其成为一个二维 4x1数组。将 4x1数组与形状为 (3,)的 b组合,产生一个 4x3数组。
- Copyright © 2003-2013 菜鸟教程。
- 版权与免责声明

Numpy 教程
- NumPy 教程
- NumPy 安装
- NumPy Ndarray对象
- NumPy 数据类型
- NumPy 数组属性
- NumPy 创建数组
- NumPy 数组索引
- NumPy 数组切片
- NumPy 数组副本和视图
- NumPy 数组迭代
- NumPy ufunc通用函数
- NumPy 数组形状修改
- NumPy 位运算
- NumPy 数组翻转
- NumPy 数组连接
- NumPy 数组分割
- NumPy 数组添加和删除
- NumPy 数组排序
- NumPy 数组筛选
- NumPy 广播
- NumPy 随机数
- NumPy 字符串函数
- NumPy 数学函数
- NumPy 算术函数
- NumPy 统计函数
- NumPy 字节交换
- NumPy 矩阵库(Matrix)
- NumPy 线性代数
- NumPy IO
- NumPy Matplotlib