当前位置: article > 正文

什么是过拟合、欠拟合现象以及如何缓解？_过拟合和欠拟合

作者：在线问答5 | 2024-06-28 18:50:06

踩

过拟合和欠拟合

前言：在讲解之前，小编必须先陈述这样一个客观事实，就是在模型训练过程中，过拟合或者欠拟合现象基本上可以看作是一个必然会发生的事件，因为我们将不同算法模型应用在同一种数据上构建某一类策略时，最终会挑出表现最好的算法模型，无论这个技术复杂与否，这个过程本身就在过拟合。挑出来的算法模型比其它模型更好，很可能是因为它对样本数据内的噪音刻画的更精准，而非发现了一些被其他策略忽视到的真实存在于数据之间的因果关系。总之，过拟合或者欠拟合现象在模型训练过程中是不可避免的，但是可以通过一些方法缓解这种现象的发生，下面小编会对这部分问题具体讲解。

1、过拟合和欠拟合现象的理解

不论过拟合还是欠拟合，都会造成算法模型预测的结果和真实结果产生较大的误差。为了理解过拟合和欠拟合是如何影响算法模型预测的误差的，我们就要理解误差指的是什么？误差可以表示成偏差、方差、噪声之和，即误差=偏差+方差+噪声，如图1所示。

图1

偏差：指的是算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力；

方差：指同样大小训练集的变动而导致的学习性能的变化，即刻画了因数据扰动而造成的影响；

噪声：表示在当前任务上任何学习算法所能达到的期望泛化误差的下界。

过拟合是指模型对训练数据拟合程度过当的情况，反映在评估指标上，就是模型在训练数据上表现很好，但是在测试数据和新数据上表现较差。换句话说，从误差=偏差+方差+噪声的角度去思考，过拟合指的就是偏差在可接受范围内而方差过高的现象，造成模型在训练数据上几乎完美，而在新数据上预测结果可能跟真实值相差过大，图2就是一个典型的过拟合模型。

图2

欠拟合则指的是模型在训练以及预测时模型表现都不好的情况，从误差=偏差+方差+噪声的角度去思考，欠拟合指的就是高偏差高方差的现象，重点在于偏差过大。出现欠拟合现象则说明该模型的特征学习能力太差，不能够学习到数据中的有效特征。

2、缓解过拟合现象的方法

缓解过拟合现象的方法有很多种，本文将从数据、模型、正则项三方面进行讲解。

2.1 数据方面

第一，可以获取更多的训练数据来训练模型，因为更多的样本会让模型学到更全面更有效的特征，从而减少噪声的影响，可以说这是缓解模型过拟合最有效的方法。

第二，如果很难再获取到更多训练数据，那么可以对已有训练数据进行合理扩充，增加数据的多样性，比如图像数据可以通过图像平移、旋转、缩放、裁剪等手段进行扩充。

另外，提前终止训练也可以缓解过拟合现象，因为在初始化网络时一般都是初始为较小的权值，但训练时间越长，部分网络权值可能越大，在合适的时间停止训练，就可以将网络拟合数据的能力限制在一定范围内。

2.2 模型方面

降低模型的复杂度。数据少时，复杂的模型是产生过拟合的主要因素，神经网络可以通过减少网络层数、神经元个数（如Dropout、BN、池化等），决策树可以通过剪枝、降低深度、减少节点数等。另外也可以采取集成学习方法（比如Bagging、Boosting、Stacking三大类集成学习方法），把多个模型集成在一起来降低单一模型过拟合的风险。

2.3 添加正则项

在优化目标函数时，通过在目标函数后面添加正则项也是缓解过拟合现象的一大途径，在这里小编主要讲解L1正则项和L2正则项两种，在神经网络优化器中的权值衰减weight_deacy参数就是L2正则，默认是0，即不添加L2正则；L1正则需要自己写代码实现，即在loss后添加L1正则项即可。添加L1正则项的目标函数和添加L2正则项的目标函数分别如下：

$Obj 1=\frac{1}{N}\sum_{i=1}^{N}f(\hat{y_{i}},y_{i})+\sum_{i=1}^{N}|\omega _{i}|$

$Obj 2=\frac{1}{N}\sum_{i=1}^{N}f(\hat{y_{i}},y_{i})+\sum_{i=1}^{N}\omega _{i}^{2}$

如果加上这种正则项，要使目标函数小，就是希望等号右侧第一项的代价函数小，同时也希望 $\omega_{i }$ 小。这样就说明每个样本的权重都很小，这样模型就不会太多的关注某种类型的样本，模型参数也不会太复杂，有利于缓解过拟合现象。

那么L1正则项和L2正则项有什么区别呢？

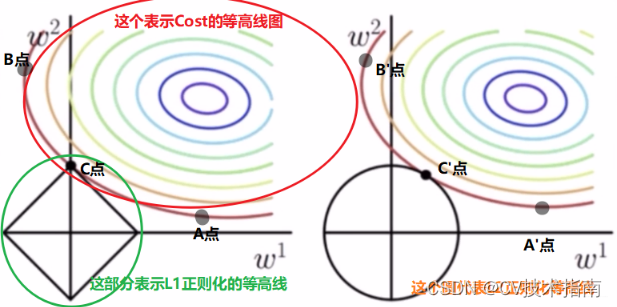
图3

如图3，左边是L1正则化的，上面彩色的是代价函数Cost的等高线图，也就是在同一条线上Cost是相等的，比如A,B,C三点，产生的Cost是相等的。黑色的矩形表示L1正则项的一个等高线， $|\omega _{1}+\omega _{2}|=r$ , 假设这里的 $r$ 取1，那么矩形框上任意一个点上正则项的值都是1。由于我们要使目标函数最小，也就是要让代价函数cost和正则项之和最小，以图中A、B、C三点的目标函数为例，由于这三点处于同一等高线上，即它们的代价函数cost的值相等，但是很明显C点的正则项比B、C点的正则项值都小，所以C点的目标函数的值最小。所以不难发现，添加L1正则项的目标函数，其最优解往往在坐标轴上，既能保证损失最小，也能保证各个特征的权重参数 $\omega$ 之和最小，同时权重参数 $\omega$ 有稀疏解，即有0解。某个参数解 $\omega =0$ ，也就是说模型会选择性忽视该参数对应的特征，让该特征不对模型预测结果产生任何影响。