机器学习——训练模型

机器学习——训练模型

线性回归

$$\begin{gathered} \hat{y}=h_{\Theta }(x)=\Theta \ast x \\ 其中\Theta 是模型的参数向量，其中包括偏置项{\Theta }_0和特征权重{\Theta }_1至{\Theta }_n \\ x是实例的特征向量，包括从x_0至x_n,x_0始终为0 \\ \Theta \ast x是向量\Theta 与x点积 \\ {h}_{\Theta }是假设函数，使用模型参数\Theta \end{gathered}$$

线性回归模型的MSE成本函数

$$MSE=(X,h_{\Theta })=1/m\sum _{i=1}^m({\Theta }^T{x}^{(i)}-y^{(I)}{)}^2$$

标准方程

$$\begin{gathered} \hat{\Theta }=(X^{T}X{)}^{-1}{X}^{T}y \\ 方程中\hat{\Theta }是使成本函数最小的\Theta 值 \\ y是包括y^{(1)}到y^{(m)}的目标值向量 \end{gathered}$$

梯度下降

批量梯度下降

$$
成本函数的偏导数：

\ \frac{ \partial MSE(\theta)}{\partial\theta_j} = 2/m\sum_{i = 1}^{m}(\ThetaTx^{(i)-y{i}})x_{j}^{(i)}
$$

$$梯度向量：{\nabla }_{\Theta }MSE(\Theta )=2/m{X}^T(X\Theta -y)$$

$$梯度下降步骤：{\Theta }^{下一步}=\Theta -\eta {\nabla }_{\Theta }MSE(\Theta )(\eta 为学习率)$$

eta = 0.1
n_iteration = 1000#迭代次数
m = 100

theta = np.random.randn(2,1)
for n in range(n_iteration):
    gradienters = 2/m*x_b.T.dot(x_b.dot(theta)-y)#偏导计算
    theta = theta-eta*gradienters #更改theta
1
2
3
4
5
6
7
8

随机梯度下降

'''随机梯度下降'''
n_epochs = 50#向前或向后迭代次数

t0,t1 = 5,50 #学习步长超参数

def learning_schedule(t):#计算步长
    return t0/(t+t1)#步长逐渐减小

theta = np.random.randn(2,1)
for n in range(n_epochs):
    for i in range(m):
        random_index = np.random.randint(m)
        xi = x_b[random_index:random_index+1]
        yi = y[random_index:random_index+1]
        gradienters = 2*xi.T.dot(xi.dot(theta)-yi)
        eta = learning_schedule(n*m+i)
        theta = theta-eta*gradienters
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

sklearn实现随机梯度下降

sgd_reg = SGDRegressor(max_iter=1000,tol = 1e-3,penalty=None,eta0=0.1)
sgd_reg.fit(x,y.ravel())
print(sgd_reg.intercept_,sgd_reg.coef_)
1
2
3

小批量梯度下降

'''小批量梯度下降'''
theta_path_mgd = []

n_iterations = 50
minibatch_size = 20

np.random.seed(42)
theta = np.random.randn(2,1)  # random initialization

t0, t1 = 200, 1000
def learning_schedule(t):
    return t0 / (t + t1)

t = 0
for epoch in range(n_iterations):
    shuffled_indices = np.random.permutation(m)
    x_b_shuffled = x_b[shuffled_indices]
    y_shuffled = y[shuffled_indices]
    for i in range(0, m, minibatch_size):
        t += 1
        xi = x_b_shuffled[i:i+minibatch_size]
        yi = y_shuffled[i:i+minibatch_size]
        gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
        eta = learning_schedule(t)
        theta = theta - eta * gradients
        theta_path_mgd.append(theta)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

多项式回归

'''多项式回归'''
m = 100
x = 6*np.random.rand(m,1)-3
y = 0.5*x**2+x+2+np.random.randn(m,1)

poly_features = PolynomialFeatures(degree=2,include_bias=False)#聚类特征
x_poly = poly_features.fit_transform(x)

lin_reg = LinearRegression()
lin_reg.fit(x_poly,y)
#画图
X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(x, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([-3, 3, 0, 10])

plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

PolynomialFeatures还可以将特征的所有组合添加到给定的多项式阶数

正规化线性模型

岭回归

成本函数
$$\begin{gathered} J(\Theta )=MSE(\Theta )+\alpha \frac{1}{2}\sum _{i=1}^n{\Theta }_i^2 \\ 超参数\alpha 控制要对模型进行正规化的程度。如果\alpha =0，则岭回归仅是线性回归。 \\ 如果\alpha 非常大，则所有权重最终都非常接近于零，结果是一条经过数据均值的平线 \end{gathered}$$
闭式解的岭回归：
$$\hat{\Theta }=(X^{T}X+\alpha A{)}^{-1}{X}^{T}y$$

from sklearn.linear_model import Ridge
np.random.seed(42)
m = 20
X = 3 * np.random.rand(m, 1)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5
X_new = np.linspace(0, 3, 100).reshape(100, 1)

ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
ridge_reg = Ridge(alpha=1, solver="sag", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
1
2
3
4
5
6
7
8
9
10
11
12
13

Lasso回归

最小绝对收敛和选择算子回归(Least Absolute Shrinkage and Selection Operator Regression)

成本函数：
$$J(\Theta )=MSE(\Theta )+\alpha \sum _{i=1}^n|{\Theta }_i|$$
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jufNfNa1-1658889211621)(data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAj4AAAEYCAYAAABcL/waAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAABUKklEQVR4nO3dd3hUVfrA8e9JgRQIkABBSghVepBEKaIGISKsiOu69oKrlLVXLKhgxYK4a0HlJwoqCurqYqEIaBQkIEFJKIIrHSQhQAgQAkkm5/fHSSWTOnf6+3meeZLcuXPvO5PJm3fOPUVprRFCCCGE8AcB7g5ACCGEEMJVpPARQgghhN+QwkcIIYQQfkMKHyGEEEL4DSl8hBBCCOE3pPARQgghhN+QwkcIIYQQfsMphY9SqotS6qRS6sNq9rlXKZWhlMpRSr2rlGrojFiEEL5B8ooQwgrOavF5A1hb1Z1KqeHAw8BQIBboCDzppFiEEL5B8ooQwmGWFz5KqauBI8Dyana7CZiltd6ktc4GngbGWB2LEMI3SF4RQlglyMqDKaUigKcwn7huqWbXnsCCcj+nAdFKqSit9SE7xx0HjAMIDw+P79atm3VBCyGcat26dQe11i3q+3hn5BXJKUJ4L0dziqWFD+YT1iyt9R6lVHX7NQJyyv1c8n1joFLho7WeCcwESEhI0KmpqdZEK4RwOqXULgcPYXlekZwihPdyNKdYVvgopfoCw4CzarH7cSCi3M8l3x+zKh4hhPeTvCKEsJqVLT6JmA6Fu4s/lTUCApVSPbTW/U7bdxMQB3xS/HMckGnvMpcQwq8lInlFCGEhKzs3zwQ6AX2Lb28B3wDD7ez7PnCLUqqHUqoZ8Bgw28JYhBC+QfKKEMJSlhU+WusTWuuMkhum2fmk1jpLKRWjlDqulIop3ncx8CLwPbCr+DbZqliEEL5B8ooQwmpWd24upbWeUu773Zgm6vL3TwemO+v8QgjfI3lFCOEoWbJCCCGEEH7DaS0+7nL06FEOHDhAQUGBu0MRdgQHB9OyZUsiIiJq3lkIDyF5RVRH8pp38anC5+jRo2RmZtKmTRtCQ0OpYc4P4WJaa/Ly8ti3bx+AJAnhFSSviOpIXvM+PnWp68CBA7Rp04awsDBJTh5IKUVYWBht2rThwIED7g5HiFqRvCKqI3nN+/hU4VNQUEBoaKi7wxA1CA0NlUsGwmtIXhG1IXnNe/hU4QPIJzIvIL8j4W3kPStqIu8R7+FzhY8QQgghRFWk8BFCCCGE35DCRwghhBB+QwofAcDmzZsZOnQoYWFhtG7dmieeeAKbzebusIQQXkzyivBEPjWPj6if7Oxshg0bRo8ePViwYAHbtm3j/vvvp6ioiGeeecbd4QkhvJDkFeGppPARvPXWW+Tl5fH5558TERFBUlISR48eZcqUKUycOFEm5BJC1JnkFeGp5FKXhzp8+DDjx4+nefPmREZG8tBDDwEwePBgXnvtNUvPtWjRIoYPH14hEV199dXk5eXxww8/WHouIYT7SF4RQlp8PNKRI0cYNGgQjRo14t1332Xjxo1MmjSJ2NhYtm3bxtixYyvsr7Wu1XXzoCD7v+4tW7Zw4YUXVtgWExNDWFgYW7ZsYdSoUfV/MkIIjyB5RQhDWnw80LPPPktGRgaLFy/m0ksv5dFHH6V58+Y88sgjPPDAA4SEhFTYf86cOQQHB9d4q0p2djZNmzattL1Zs2ZkZ2db/fSEEG4geUUIwy9afNw5oabWdd1fM2fOHMaOHUvz5s1Ltzdp0oScnBwmTJhQ6TGjRo1i7dq1DsVpb9ZRrbXMRipEFSSv1EzyivBEflH41DVJuNPWrVvJysoiKSmpwnabzcbdd99NeHh4pcdERkbSpEmTep+zWbNmHDlypNL2nJwcu5/YhBCSV2oieUV4KrnU5WF27NgBQPv27Uu3rVq1ip07d9K3b1+7j3G0Sbpbt25s2bKlwrY9e/aQm5tLt27dHH9SQgi3krwiRBnLW3yUUh8CQ4FwIAN4UWv9jp39xgCzgLxymy/RWidbHZM3CQwMBMzoCzDNwhMnTiz93h5Hm6RHjBjBSy+9xLFjx2jcuDEA8+fPJzQ0lAsuuKDexxXCCpJTHCd5RYhytNaW3oCeQMPi77thElW8nf3GACvrevz4+Hhdlc2bN1d5n7c4ePCgDgkJ0YMHD9aLFi3SY8aM0d27d9ddunTR1157rd6xY4fl5zx8+LBu1aqVHjZsmF66dKl+++23dXh4uJ40aZLl5yrhC78rUTtAqvbSnKK1b7xX/SWvuJsvvFe8gaM5xfJLXVrrTVrrUyU/Ft86WX0eXxUVFcWcOXPYu3cvl156Kenp6XzzzTdMmjSJBQsW8Mknn1h+zmbNmrF8+XJsNhujRo1i8uTJ3HvvvTz55JOWn0uIupKc4jjJK0KUUdoJPfSUUjMwn75CgV+B87XWx0/bZwzwBqZZ+jDwATBVa11o53jjgHEAMTEx8bt27bJ73t9++43u3btb9jyE88jvyn8opdZprRMcPIZbcgrIe1XUnrxXXMPRnOKUzs1a69uAxsB5wOfAKTu7/Qj0AloCfwOuAR6s4ngztdYJWuuEFi1aOCNkIYQHk5wihLCK00Z1aa1tWuuVQFvgn3bu36613qG1LtJabwCeAq5wVjxCCO8mOUUIYQVXDGcPonbX4zUgs1oJIWoiOUUIUW+WFj5KqZZKqauVUo2UUoFKqeGY5ubv7Ow7QikVXfx9N+BxYIGV8QghvJvkFCGE1axu8dGYJui9QDYwDbhHa71AKRWjlDqulIop3ncokK6UygUWYq7bP2dxPEII7yY5RQhhKUsnMNRaZwF2Z6bSWu8GGpX7+QHgASvPL4TwLZJThBBWkyUrhBBCCOE3pPARQgghhN+QwkcIIYQQfkMKHyGEEEL4DSl8BACbN29m6NChhIWF0bp1a5544glsNlu1j/njjz8YP348cXFxBAYGkpiY6JpghRAez1PzQ21yXWJiIkopu7eUlBQ3RS6sYumoLuGdsrOzGTZsGD169GDBggVs27aN+++/n6KiIp555pkqH7dp0yYWLlzIgAEDyM/Pd2HEQghP54n5oba5bsaMGRw9erTCY5944gl+/fVXzj77bFeHLSwmhY/grbfeIi8vj88//5yIiAiSkpI4evQoU6ZMYeLEiURERNh93KhRoxg9ejQAV1xxBQcPHnRl2EIID+aJ+aG2ua5Hjx4VHpefn09qaipXXXUVQUHyb9Ndftz1Iy+tesnh48ilLg91+PBhxo8fT/PmzYmMjOShhx4CYPDgwbz22muWnmvRokUMHz68QoFz9dVXk5eXxw8//FDl4wIC5O0jhDdxZV6pbX4oLCzkpZdeonPnzoSGhpKQkMDKlSstjaVEfXPd4sWLyc7O5pprrnFKXKJ2vtvxHV///rXDx5HS1QMdOXKEQYMG0ahRI9599102btzIpEmTiI2NZdu2bYwdO7bC/lrrGvvjAFV+UtmyZQsXXnhhhW0xMTGEhYWxZcsWRo0aVf8nI4TwCK7OK7VRWFjIxRdfzObNm5k8eTIdO3bknXfeYeTIkfzvf/8jOjq63se2p765bt68ebRp04bzzjvP0nhE3fy05ydLjuMXhY96sup1Ct++5G3GxY8DYOa6mYz/enyV++rJuvT7+Jnx/LL/F7v7je03lpmjZtYzWnj22WfJyMjgjz/+oHnz5lx66aW88sorPPLIIzz++OOEhIRU2H/OnDncfPPNNR5Xa213e3Z2Nk2bNq20vVmzZmRnZ9frOQjh6ySvFMdfRV6pjZdffpk1a9awbt06unbtCpiOxTExMXz22Wfcfvvt9T62PfXJdSdOnOCrr75i3LhxKCVr3rqLrcjG6r2rLTmWXxQ+3kRrzZw5cxg7dizNmzcv3d6kSRNycnKYMGFCpceMGjWKtWvXOnRee3/QWmv5QxfCB7grr1SnqKiIl19+mRtvvJGOHTtSWFgImFzUuXNndu/eXekxOTk57N+/v8Zjd+vWrcr76prrvvrqK44fPy6Xudxsw4ENHM8/ToemHdjBDoeO5ReFT/lPVNUZFz+u9FNaTdaNW+dISFXaunUrWVlZJCUlVdhus9m4++67CQ8Pr/SYyMhImjRpUu9zNmvWjCNHjlTanpOTY/fTkRBC8oqjNmzYQFZWFjNmzGDGjBmV7r/44osrbfv0008rXZKzp6pWqPrkunnz5tG5c2cSEhJqPK9wnlV7VgEwqN0gKXx8zY4d5hfavn370m2rVq1i586d9O3b1+5jHG2S7tatG1u2bKmwbc+ePeTm5lb7yUkI4R3ckVdqUtJys2zZMrsFVvlYS9x6663ceuut9Tof1D3X5eTksGjRIiZOnFjvcwprlPTvObfducxlrkPHksLHwwQGBgJm9AWYpFLyR1dVgnG0SXrEiBG89NJLHDt2jMaNGwMwf/58QkNDueACuwtjCyG8iDvySk3OOOMMAJo2bUp8fLzTzlNeXXPdF198walTp+Qylwe4b8B99I3uy0WdLnL4WFL4eJj4+HhCQkKYOHEikyZNYv78+Rw+fJguXbowb948evfuTWxsbIXHREVFERUVVe9zTpgwgVdffZXLL7+chx56iO3btzNlyhTuu+++0mGf77//Pv/4xz/Ytm1b6SexEydOsHDhQgD27dvH0aNH+eyzzwAYOXIkYWFh9Y5JCGEdd+SVmvJDz5496du3L9dee23p6LKsrCx+/vlnevTowU033VTvc1elNrmuvHnz5hEXF0f37t0tj0XUTXzreOJbW1Qga6296hYfH6+rsnnz5irv8ybz58/XsbGxOjg4WPfr109v375dz549W4eHh+sXXnjBKefctGmTHjJkiA4JCdGtWrXSjz32mC4sLCy9/7333tOA3rFjR+m2HTt2aMDurfx+9vjK70rUDEjVHpA7qrpVl1O09p33qqvzSm3yw549e/S1116rzzjjDB0SEqI7dOigr7vuOr1161bL4ylRU64rkZWVpYOCgvTUqVNrfWxfea94OkdzitIODEV0h4SEBJ2ammr3vt9++00qcy8hvyv/oZRap7X22J6h1eUUkPeqqD15rzjH/637PzKOZ3Bt72vpFNnJ4Zxi+dS7SqkPlVL7lVJHlVK/K6Wq7ImmlLpXKZWhlMpRSr2rlGpodTxCCO8mOUUI/zYjdQZPJD/BziM7LTmeM9YcmArEaq0jgEuBZ5RSlS7MKaWGAw8DQ4FYoCPwpBPiEUJ4N8kpQvipw3mHSctIo0FgAwa1G2TJMS0vfLTWm7TWp0p+LL51srPrTcCs4v2zgaeBMVbHI4TwbpJThPBfP+76EY1mQNsBhAaHWnJMp6wyqZSaoZQ6AWwB9gML7ezWE0gr93MaEK2UqjSMQCk1TimVqpRKzcrKckbIQggPJjlFCP/0/Y7vARgSO8SyYzql8NFa3wY0Bs4DPgdO2dmtEZBT7ueS7xvbOd5MrXWC1jqhRYsWVocrhPBwklOE8E/f7/SSwgdAa23TWq8E2gL/tLPLcaD8xAkl3x9zVkxCCO8lOUUI/5KVm8WGAxtoGNiQ/m37W3ZcV0xgGIT96/GbgDjgk+Kf44BMrfUhF8QkhPBeklOE8AO5Bblc1/s6inQRIUEhlh3X0sJHKdUSuBD4GsgDhgHXANfa2f19YLZSai7mmv1jwGwr4xFCeDfJKUL4r9imsXx4+YeWH9fqS10a0wS9F8gGpgH3aK0XKKVilFLHlVIxAFrrxcCLwPfAruLbZIvjEUJ4N8kpQghLWdrio7XOAuyuaqm13o3pfFh+23RgupUxCCF8h+QUIfxTVm4WP+76kaEdh9I0pKmlx3Za52YhhBBCiPr4+vevueLTK7jhixssP7YUPoI//viD8ePHExcXR2BgIImJie4OSQjh5SSvCEcs2bYEgOGdhlt+bFeM6hIebtOmTSxcuJABAwaQn5/v7nCEED5A8oqoL1uRjW+3fQvAxZ0vtvz40uIjGDVqFHv27OHTTz+lZ8+e7g5HCOEDJK+I+lr751qyT2bTqVknOkd2tvz4Uvh4qMOHDzN+/HiaN29OZGQkDz30EACDBw/mtddes/RcAQHyNhDCH0heEd5gyR/Ou8wFcqnLIx05coRBgwbRqFEj3n33XTZu3MikSZOIjY1l27ZtjB07tsL+WmtsNluNxw0Kkl+3EP5K8orwFou3LQacc5kL/KXFRylzK2/UKLPtq6/Kts2cabaNG1e27c8/zbbWrSs+Pj7ebF+3rmzblClm25QpDoX77LPPkpGRweLFi7n00kt59NFHad68OY888ggPPPAAISEVZ7CcM2cOwcHBNd6EEBaSvCJ5RViuwFaArchGw8CGDOlg3fpc5Ump7mG01syZM4exY8fSvHnz0u1NmjQhJyeHCRMmVHrMqFGjWLt2rSvDFAKAlBRITobERBg40N3RiKpIXhGerqgIsrIgOjqYf/f6mUUZeWxYF+qUvOIfhY/WlbeV/0RWYty4ip/KwHwis/f48p/ISkyZ4vCnsq1bt5KVlUVSUlKF7Tabjbvvvpvw8PBKj4mMjKRJkyYOnVeIukpJgaFDIT8fGjSA5cv9rPiRvCKEZebNg+uvh5Yt4eBBgFCmTXVOXvGPS11eZMeOHQC0b9++dNuqVavYuXMnffv2tfsYaZIW7pCcbIoem818TU52d0SiKpJXhKf76CN47/18Lro8A5tNOzWv+EeLjxcJDAwEzOgLME3UEydOLP3eHmmSFu6QmGhaekpafGR+Os8leUV4ssOHYcUKGPt8Mh8kT0YFJaOKGjotr0jh42Hi4+MJCQlh4sSJTJo0ifnz53P48GG6dOnCvHnz6N27N7GxsRUeExUVRVRUVL3PeeLECRYuXAjAvn37OHr0KJ999hkAI0eOJCwsrN7HFr7l9D49y5dLHx9vIHlFeKqUFHjpJUhIgG93LYB2qzln/Bxsa8bx6qtOyitaa6+6xcfH66ps3ry5yvu8yfz583VsbKwODg7W/fr109u3b9ezZ8/W4eHh+oUXXrD8fDt27NCYVbAr3Xbs2GH5+bT2nd+VP1m1SuvQUK0DA83XVatq9zggVXtA7qjqVl1O0dp33qv+kFfczVfeK65SklNA6wYNinTzO0dppqDfWbhWJyRU/ThHc4q0+HigK6+8kiuvvLLCtg4dOnDTTTc55XyxsbFVNncLUcJenx5p5fEekleEpynJKQCFNji4uSdtRv7C38+N567NUFgIzpgmSjo3CyFqpaRPT2Cg9OkRQjguMRECAsw0VQFBBRCbzGXdLiMiQnHGGfD77845r7T4CCFqRfr0CCGsNHAgnHUWdOmiWRl9E7siVjP6zKcA6NsX0tKgRw/rzyuFjxCi1gYOlIJHCGGNoiLYuhVmfvwn33y6mOYBzUmMTQQgLs4UPtdcY/15Lb3UpZRqqJSapZTapZQ6ppT6VSk1oop9xyilbEqp4+VuiVbGI4TwbpJThPBdW7ZA8+YQ17ENmQ9k8v1N3xMcaOaG6tsX1q93znmtbvEJAvYAFwC7gZHAJ0qp3lrrnXb2T9FaD7YyAK016vT1c9zg+HE4dgwaN4ZGjdwdjWeRDo+iDtyeU0DyiqiZ5LW6W70aBgww3zcIbECvlr1K7ytp8XEGS1t8tNa5WuspWuudWusirfXXwA4g3srzVCU4OJi8vDxXnKpax4+bTln79pmvx4+7OyLPkpeXJzO+ilpxd04BySuidiSv1V1KCvQ8J4tjp45Vuq9dOzh5EjIzrT+vU0d1KaWiga7Apip2OUspdVAp9btS6nGllEMtUC1btmTfvn2cOHHCrdX3sWPm2iWYr8cq/079ktaaEydOsG/fPlq2bOnucIQXcnVOAckronqS1+pv9WpIb/IM0dOimbN+ToX7lCrr4Gw1p3VuVkoFA3OBOVrrLXZ2+RHoBewCegLzgUJgqp1jjQPGAcTExFR5zoiICAD+/PNPCgoKHHsCDjh1Cg4dMmsQKmXmIThyxG3heJTg4GCio6NLf1dC1JY7cgpIXhE1k7xWdzk5sH2njYNZn5BXmEePFpWHb5Vc7rroImvP7ZTCRykVAHwA5AN32NtHa7293I8blFJPAQ9iJ0lprWcCMwESEhKq/cgVERHhEW++8lP7V7EGoBCiltyZU0DyihBWW7sWOly4nE25GXRq1omE1gmV9omJgT17rD+35YWPMj0AZwHRwEitdW0/ImnA/b0HLSLDfoWwhuSUMpJXhK9YvRoK+8wCYEzfMXYHDzRv7pyRXc7o4/Mm0B0YpbWuskegUmpE8fV6lFLdgMeBBU6IRwjh3SSnCOFjflh7iG3B/0WhuCnO/rIpUVFw8KD157Z6Hp/2wHigL5BRbi6N65RSMcXfl1xQHwqkK6VygYXA58BzVsYjhPBuklOE8D1aw6qjH1Go8xneeTjtmrSzu19UlOnXZjVLL3VprXdRfdNyo3L7PgA8YOX5hRC+RXKKEL5n+3ZQrTYA8I++/6hyv+bNnVP4yCKlQgghhHCZX36BYXkz2XrHVi4989Iq93PWpS5Zq0sIIYQQLvPLL9CvH3SN6lrtfk2aQG4uFBaa6RusIi0+QgghhHCJIyeP8N3WNfTrV/O+AQHQrBkcPmxtDFL4CCGEEMIlZv3yLj/HDeDzvDtrtb8zLndJ4SOEEEIIp7MV2fh3yusAXNYnqVaPccbILil8hBBCCOF0C/+3kD3HdxB6sgN/6fKXWj3GGSO7alX4KKXeUkpppVRrO/edqZTKV0r929rQhBBCCOErXvv5NQDODb6DwIDAWj3GnZe6Uoq/nmPnvleAo8AUKwISQgghhG/5df+vLN2+lEBbODf2vrnWj3Pnpa7VxV8rFD5Kqb8AI4AntNbZVgbmLVJSYOpU89VfyWsghHXk70leA1/03EoziXrDDRO4oH+zWj/OGZe6ajUyXmu9VSl1mHKFj1IqGJgObATetjYs75CSAkOHQn4+NGgAy5f73wKC8hoIYR35e5LXwBdprekS2YXIkOboX+6jnf0VKuyKioItW6yNpy6dm1cDCapsCdW7ga7APVprm7VheYfkZPPHabOZr8nJ7o7I9eQ1EMI68vckr4EvUkrx3NDneKf7XhLObI2dhdir5O5RXauBJsCZSqmWmJWP/6u1Xm5tSN4jMdF8IgkMNF8TE90dkevJayCEdeTvSV4DX7ZhfcNaTVxYntsudRUr38H5fKAhcL+14XiXgQNNM2xysvnj9MfmWHkNjJQUeQ2E4+TvSV6D8nwhrzyy7BFim8byj7P+wdq1wYwZU7fHO2NUV10KnzVAEXALMBh4SWu93dpwvM/Agd77hrSKv78G0iehssxMWLYMVq50dyTex9//nkBeA/CNvLI5azMvrnqRABXA0A7DSE3txOuv1+0Ybr3UpbU+BmzGtPYcAJ61NhQhvJP0STALCS5aBPffD336QLdu8J//QO/e7o5MCO/kC3nlse8eo0gXMbbfWEJPdqKwEGJi6naMyEg4cgSKiqyLq67rnf4M9AIeKS6EhPB7JX0SSj6Z+UOfBJsN1q2DpUtNy05qqlltOSkJZs6EhISy1ZRvv929sQrhjbw9r6zZu4YvtnxBWHAYj5//OD9/B2efTZ06NoPJI40ameInMtKa2Gpd+BQPX08EUoE51pxeCO/nD30StIZt20yRs3QpfP89tG5tCp0HH4TzzzfJSQhhDW/OK1prHlj6AAD39L+HMxqfQWqq+UBUHyWXu1xe+AAPAB2A67TW2prTC+EbfLFPwqFDJvGWtOrk58OwYfDXv8Lrr8MZZ7g7QiF8m7fmlbkb5rJy90pahrfkwXMfBGDtWrjttvodr3lz08G5Sxdr4qu2j49SKlIpdY1SairwNDBda726mv0bKqVmKaV2KaWOKaV+VUqNqGb/e5VSGUqpHKXUu0qphvV/KkIIR+TlmSLnoYcgPh46doQPPoBeveCbb2DvXpgzB66/3nVFj+QUIbzP3A1zAXhh2As0DWmK1ljS4mOVmlp8hgMfYTozvwI8XIvj7QEuAHYDI4FPlFK9tdY7y++olBpefLwLgT+BL4Ana3EOIYQFiopg/fqyFp3Vq01n5KQk+Pe/oX9/CA52d5SSU4TwNl9d8xWfbvqUq3pdBcCuXdCwobk8Xh9Wz+VTbeGjtf4Y+Li2B9Na51JxsdKvlVI7gHhg52m73wTM0lpvAlBKPQ3MRZKUEE6zc2dZP53ly80nqaQkuOMO+OwzaNLE3RFWJDlFiJpt2wZvvQULFkBBgZn8MTER7rrLjLJ0taCAIK7pfU3pz4609oD1c/nUZebmOlNKRWOWtdhk5+6eQFq5n9OAaKVUlJ3jjFNKpSqlUrOyspwTrBA+KDsbPv8c/vlPc328f3/TMfnii+HXX2HrVtNfZ/Rozyt67JGcIkSZkydh3DgYMMD8/Omn5gPNV19Bhw4wYoT5287JcX4sBbYC7l9yP/uP7a9039q1jhc+Vrb4OK3wKR4FNheYo7W2t8RYI6D8r6Pk+8an76i1nqm1TtBaJ7Ro0cL6YIXwEadOmVEgjz1mipyYGDO8vHNn06Kzfz/MnQs330ydFgr0BJJThCizZ48ZTXnkCOzYAS+9BHFxpm9e9+4waZLZ3q6d6SC93cnTDU9dOZXpq6cz6uNRnD7+ydEWH5de6qovpVQA8AGQD9xRxW7HgYhyP5d8L/MDCVFLWsPGjWX9dFauNJMHJiXB88/DoEHm2rp7YtPYLFq/WHKKEGV27oTBg82lrAcfrHpunAYNTIvuG2/AueeaD0Vnnml9PGkZaTz949MATLtoGqpcQIWFpvA555z6H9/qS12WFz7Fq7fPAqKBkVrrgip23QTEAZ8U/xwHZGqtLZ6cWgjfsm9fWT+dZcvM/DnDhsEtt8CHH1o310VdnCo8xW8HfyMtI430zHTSMtNIy0xj0nmTHD625BQhymRnw8iRpuC5++7aPeb22yEkBEaNgjVroFkz6+I5nn+cqz67isKiQm4/+3YSYxMr3J+eDm3bmuKlvlw9qqs+3gS6A8O01nnV7Pc+MFspNRfYDzwGzHZCPEJ4taNHzSe1ZcvMLTPTrOEzbBg89ZRp2nYVrTWZuZm0atSqdNvoeaNZ+L+FFBYVVtp/y0F7V6TqTHKKEJhL2ZddZvro1bboKXHLLbBhA1x1FSxcWDazuiO01tz2zW1sPbSVni168mLSi5X2WbHCtE45wqMvdSml2gPjgVNARrnmrvHACsxaXz201ru11ouVUi8C3wOhwH+AyVbGI4Q3KiiAn382LTpLl0Jamumvk5Rk5tXp29eM2nA2e6046ZnpZJ3IIvOBTFqGtwSgYWBDbEU2ukZ1JS46jj7RfYiLjiOuVRztItrxNm/XOwbJKUKUefhh01ozbVr9Hj9tGvzlL/DEE/Dcc47HM3v9bD5I/4Cw4DA++fsnhAWHVdpnxQpTrDkiMtKDCx+t9S6gupU4Kkxqr7WeDky3MgYhvI3WsGVL2eWrH34wrThJSTB5svm0FFY5nwBmBWdHp7TXWpNxPIO8wjw6NjPNR2v2rmHwe4PttuI0adiEXUd2lRY+r454ldmXzbab9BwlOUUIY+lSM0AhLQ0C6jksKSgI3n/fDHG//HL7HY7rklOOnDyCQvHGyDfo0aJHpfu1Nv0O61uolQgPhxMnHDtGeU7p3CyEqF5GRsXlIAIDTaFz7bUwaxbUZqBRSoq55FWyiOHy5TUnqpJWnPTMdNOSc8B8zTqRxeXdL+c/V/4HgE6Rney24vSJ7kNMk5gKnRfLX/YSQljv0CEzEnP2bMf78EVHw/Tp5nipqRUHP9Q1p9w78F6GdBhC31Z97d7/xx9mEtT27R2LOTwccnMdO0Z5UvgI4QK5ufDjj2WFzp495hNVUpIZdtq5c91XLU5ONgnKZjNfk5MrJqmM4xmkZaQxsN1AIhqaAU43/vdGPtn0SaVjNWnYhJCgkNKfm4c15/ijx53SiiOEqJs77oC//93067PCtdfC/Pnw7LOmn2CJmnIKmM7MB08cJLZpLECVRQ+Y1p7Bg+ue205XMoN8QYE1s8lL4SOEE9hssG5dWT+d1FSz/lVSEvzf/5nvHe1cmJhoPpXl52uCgjV5bRZz/5LlpB9IJz0znQO5BwBYdsMyhnYcCkBcdBzrM9ZXaMGJi46r1IoDSNHjJLt3mz5c27aZT9s33WTtKBvhW5YuNcvJbLI3ZWc9KWVmeu7Tx6y917Wr2V6WU8zXxMSKjztZeJLR80aTnpnOV9d8xYC2A6o9z4oVcN551sRc0urTtKnjx5LCRwgLaG3+kZX00/n+e2jTxnxCmzjRTDTWqFHNx6lJ5vFM0jLTyCvIY/TA0SxfDt98e4Jn9wzj6R2rYUfZvhENI+gT3adCQfPI4Ed49LxHHQ9E1MvHH5u5VwYPhk6dzAi9p56CG280n77Dw90dofAkJ0+aFc1fe63qfn711bq1WZD4vvvg66/NtoEDzeUte318CmwFXP3Z1Xy34ztaNWpF87DmNZ5jxQq45x5r4g0LM/18pPARwo0OHoTvviu7fHXqlGnRuewyM2mYoyuYb8/ezk+7fyodTZWWmVbaitM5sjOju41m4EAYODCcH94LolWjK+jTsg9xreKqbMU5/WfhGkVFcO+9ZpX7ZcvMDLsl9u0zxfHFF5v7IyKqPo7wLy++CL16wSWXOOf4d99tWqAXLTLLWwDFOaXifvm2fG744gYWbF1As5BmfHv9t3SO7FztsTMyTI7s1cuaWMPCrOvnI4WPELWUl2euWZe06mzbZppxk5LMP7Xu3et3LbukFSc9M52LO19Mr5YmU8xNn8sTyU9U2LekFeesVmehtS4tZFbcvMLh5yec59VXzcRxa9dWvqzVpo2ZpuDOO03H0sWLHZvsTfiGnTvh3/82a+o5S4MG8MorplVm6FDz8+nyCvL4+6d/55v/fUNEwwgWX7+Y3tG9azz2smWmpbu+I9BOZ+XILil8hKhCURGsX1/WT2f1anNNPCnJ/CPr37/uHe201nyQ/kGFeXFKWnEAAlRAaeEzOGYwf+v+t9I5cfpE96F9k/bSauNltmyBZ54x75+q+vIEBJhWwnvvNRPMffutdf8whHd65BFzWTQmxrnnGTnSvPdmzKh8WUprzV/n/5Ul25YQFRrFkuuXEN86vlbH/eoruPRS6+KUFh8hnGTnzrIWneXLzbDyYcNMAvrPf2q/gnn5Vpz9x/bz8vCXAXOp6eFlD7P/eNkKxiWtOHHRcfQ7o1/p9iEdhjCkwxArn55wscJC03n56afNyL3qKGXmO7nwQrPg5EMPuSZG4XlSUkz/mHfecf65lDLvtwsvrNzRXinFNb2uIT0znaU3LKVny561OmZ+vineX33VujilxUcIi2Rnm47IJf10jh41hc6IEeafUG1XME/PTOeDtA9K16gq34qjUDw15CnCG5ieq7effTtFusgUO63ipBXHh732mumzM2FC7fYPCjLrrZ19tulc2r+/U8MTHkhr0+HYlZ3de/UyfROfe84UQZnHM4luFA3ATX1v4rJul9EkpJaf+jBTd3TrZuYMsoq0+AhRT6dOmU9TJa06v/1mVi0eNgz++U/o3bvqfjqZxzMrXKIa3mk41/W5DoAd2TuYllI2PWlJK05JZ2ONLr1v0vmOL9wpPF9+vimev/mmbn2/YmLgzTfhuuvM2kqhoc6LUXieTz4x750bbnDteZ98Enr2LuTEwMnM2fJvUm5JKe3LU5eiB+DLL82CqFaSFh8haklr2LixrJ/OTz+ZTyJJSfD88zBoUMWZS083dcVUvt/5faVWHIDAgMDSwuecNufwZOKTpf1xpBVHfPQR9Oxp1larq8svNy0/06bB449bHppXOXIEfvnF/NPLz4czzzQDCXyxD1R+Pjz6qBlp5erndzR4K+F33syMDSkEqABW711dq07Mp9PaFD4lQ+StUjKc3QpS+Aifs3dv2Urmy5aZTwpJSXDrrTB3bsUp3zOPZ5K217TgpGems+HABlbevLL0stQPu35g6falADRu0LjCxH8D25WN+Tyj8Rk8cUHFEVjCfxUVmUsG//53/Y8xfbqZ6PKmm5zfwdXT2GwwZ44Z7ZaaCmedZS4ZBgaaifwOHTLD/x98EPr1q/l43uLtt81kghde6LpzFtgK+Nfqf/FE8hOc5CQBua359/kfMTb+gnodb+NGU7T1rF13oFqzctkKKXyE1zt61Ey4VdJP58ABMzQzKcl0Ku3QoeL+m7M2c++Se0nLSCMzN7PS8TYe2Ej/tqZzxQODHmBCwgTiouOIbRorrTiiVhYtMkODhw6t/zFiY80Q9wceMJc//MWSJeY5R0aar0OHVp6878AB0yJ26aXm8vTrr5sJIb3Z0aOmX8+SJa4756/7f+X6L65nc9ZmAMb0HcPAnOnMnNKM20bWr9Xpyy/N78XqVCktPsKvFRSYOVFK+umkpZlOoElJJhm26XqADQdMK87k9WmkLUljQJsBvD3qbQBCg0L5dtu3QFkrTklLTsmw8RLDOlq0OI7wK9OmmUkJHU3+EydCjx6ms+j551sTm6cqLISHHzajJ//1r+r/ebZsaToA3367KXoGDDBTBowbZ/0/XFeZNg0uuqji5JbOFhUWxY7sHXRq1onXRrzGiC4j0Bree9Os4j5mTN2OZ7PBu++alnWrSYuP8Ctam7lQSvrp/Pij+XQ3ZFgBj08O4PzBgYSFwWPfPcYlybPI+Dqj0jECVWDp97FNY/nvVf818+I0bU+A8sHOAsJtdu0ynZKvuMLxY4WFmVbLRx81w5u99Z96TbKz4corzfepqbWfwLFhQ7j/fjMXzQ03wA8/wHvvVd9vzxPt3w9vvGH6MjnTz/t+5sP0D3ll+CsEBgQS0ySGpTcsJaF1Ag2DzIumlLlEe9ll5laXJSK+/NIUpQOqX8KrXsLCTH8vK0jhIzxSRoaZR6fk8hXhB+g9LJ0WI9O5+Lo0th5J47WszVzVcyVhYecAZlr1jOMZNG7QmN7RvU0LTnF/nPKd9JRSjO422k3PTPi6efPgb3+zZhVpMCtpP/+8mdG5ZFkBX3LkiGmtHTjQzCJcn8V7u3c3heGNN5pWky++qNiXz9M99ZRpXWnf3vpj59vyWbBlAa+vfZ0fd/0IQELrBG6MuxGAc2POrfSYc86B0aNNUTlrVu3P9corZhJOZ5AWH+FzcnNNS87ipQV8uzKLjP+1ZsgQOOfCTBZ270vWyQz2ARwovhX74/AfnNPGFD539b+LCQkTiG0aW6EVJyUFXvuw8qJ7QjjDxx+bSzVWCQw0/xgfe8x06PWlVp+jR81zOvdc85o58txCQ2H+fHN58LzzzPxcLVtaFmoFKSn2F/Ksj61b4bPPTKu2ldIz0/kw/UPeT3u/tC9jRMMIJsRPqNUl/BdfNP2nFi82v6OapKaa1s7LL3c0cvs8to+PUuoOYAzQG/hYaz2miv3GALOAvHKbL9FaJ1sZj/BchYWwdNUBPvkhnR9/T2P3yXQatk/jZJPNdL6mN1l3riMoCIp0C557PpdGDRpVGFEVFx1Hr5a9aNywcekx20a0rXSelBTTOTI/33Q2Xb5cih9v4m055bffICvL/OO10uWXm8nlPv/ctCb5gvx806rQt6/jRU+JgADTVyYszMzN9d130LzmRcTrxOqc8uijphO3o+uzaW3mCisZgHHd59ex8cBGAHq26Mn4+PHc1PcmIhrWbhXcxo1Na8/NN5tLtzXNWv/KK2aG+/q02NWGJ7f4/Ak8AwwHapp2K0VrPdji8wsPVGArYMvBrZw40IpfVjZn6VJYdOJJTg6cYnYonsq/sHj/oIanCAzUgCJABbDlji20atSqXn1xkpNNgrLZzNfkZCl8vIxX5ZSPPzZ9VQIDa963LpQyfX0eegj++lffmMPmrrvMP9cZM6xvxXrySTMIIinJtPzUpZ9KTazMKSkp8PPPZlBGfezO2c0PO39g2Y5lfLvtW5besLR0rb/bEm5jw4ENXN/nega2HVivEalDh5pO5tddZy4fVnX5duVK0y1hxoz6PY/asLLFB6215TdMoppdzf1jgJX1OXa86euqK7jkErPtyy/Ltr39ttk2dmzZtn37zLYzzqj4+H79zPbU1LJtkyebbZMnl21LTTXb+vWr+PgzzjDb9+0r2zZ2rNn29ttl27780my75JKKj/eh53Tg+AG9bNuy0ufUfmqcDpgcrJmCXhTVR2vQ3937pX79xw91o+ca6edv7Kg16E2XDdY/7f5JHz151NLntGqV1qGhWgcGah3KCb2KAS79Pa1apfVzz2m9asEBj/o9OfKcStXy9wSkaj/IKUVFWnfpovWaNZVfA621w7/XolvN7/WXCZ7xe3XkOc2YoXWPHlqfusl579WiW8fqu+7S+oILtD653fNyis1W9+dku/UWfdfbH+ve136ku98ySmvQ+xqhmWJur615zfL3Xn6+1ovamedke7Pyczox9BJ9xhlaL1pUvN2J771b+lqTU9zZx+cspdRB4DDwATBVa11Yw2OEhyiwFbD10Fby9q3l7OJtJ05oYl/pxAnbsdIFGnadSgMF7cI70r0HsAKGDIHBg67kn4OvIeD/3oH3x9OjRXdoN6j4Uccsi3PgQNMUnZwMiS9fycBDqy07dk1SMjuWNYkHR7GcAQxkl8vO74fcmlPWrzetAGefXeOu9VLygf2bhdBXe29fn3XrYMoUM4t6gxeddx6lzOWXq66Cu++Gtyw6rlU5Zd48uPa0bUW6iFOFJwkFvt32LcuWruDYqWO8yVkArM7sxKt3XAqFDSBwNCkMpWvQr0xLepbhnYfTs0VP4D1Hnl4lwcHmsiHvmZapS66s2HF8bSrcO6l2/YAcdfKkNcdRpniyllLqGaCtrvp6fEdAA7uAnsB84AOt9dQq9h8HjAOIiYmJ37VL/nnYY2WHu/KOnDxC6p+pFdap2py1mXxbPg0CGjI5+DjfLQtizRoIGjOCRlE5xLeNI6l3HP1aV+6L4y+mTjXLDdhs5tLH00/DI4+4OyrXU0qt01onOHgMj88pzzwDhw+bGZedpajI9Il5/nkzhNvZrM4pOTlmFubp081QaVc4edKM9DrnHNP/xx3ybfkczjvMoROHOJB7gD3ZB3joxrP45M2unHcefLzhY55IfoLdObvJt+VXeGxwQDC5j+YSHBjM1Kkw6bEidFEAgYGaJ5/STHrUNdc9jxwxfZG++AKuv95MIrl4sZm2YeZM5xfimzeb/m2//eZ4TnFLi4/Wenu5HzcopZ4CHgTsJimt9UxgJkBCQoL1lZoPsKLDXUkrTlpGGl2iupSOlvr696+54YvKK+YF5HSkwbE+7AjL4a67okhMhIiIRRY8G9+QmGh+FyW/k8REd0fkuzwhpyxeDE84edWSgACYNMkU0SNGOPefjdWdeLU2q9RffLHrip58Wz460MbcT4tIHGKjXZcirr/Bhk3baBDYgKYhTUv325G9g8KiQgqKCiiwFVBQVEC+LZ98Wz7xZ8QTFWZ6H6/eu5pf9v9CXkEeJwpOcKLgBLkFueTm59IstBnTLppW/Hw1nV7txIHcA+QWVO6VG3fuvznvvK5mXzR/HP4DgJbhLenYrCNdIrvQJbILPVr0KF3kODERQhoGFP9OFBcOcV2zX9Om8M47MHmyKXR69zYtaq1aueb8vrhIqenJKuqtPh3uVuxaQeqfqaRlppGWmVbaigNw5zl3ck6bc8jOhoMbzyI6fyB5O+Mo2t+HgR3i+Ou5vRh1SwRtKw+kEsUqNIknSqdqF3NpTsnOhvR018yufMUV5p/P9987d02n2uaUAlsB2SezOXLyCEdOHqFrVNfSguLHXT+yas8qcvNzWZt2gp+DT/CXoXlc/dlJIkMjmfGXst6wQ98fyuG8wxTYCigsKqxwe3jww9xxzh0ALNiygBu+uAGbtlGki7AVma9FugiN5tDEQ0SGmmsxl3x0Selae1wF92TAPS+ZH//W/W98duVnAOw9updub3Sr8rX49vpvSeqUBMB/t/yXF356we5+sU1jSwsfpRTH8o+RW5BLoAokMjSSqLAoIgJbsv6nFtw+Nrb0cSM6j2DTbZto36R96TqB9nhCTmnXzhTerhYW5qGjupRSQcXHDAQClVIhQOHp19mVUiOAX7TWmUqpbsDjwKdWxuJvqmpdKLAV8Puh30nLTGND5gaevvBpggLMr/3h5Q+zas+qCseJbdKBtkFx7FgVT/8ppllx0KCePJi0iqSrTJXvrX0L3GHgQCl4HOEtOWX5chg8GEJCnH+uwECztMNzzzmv8CnSRfQ+J5ug4KZoFEHBmsREM1Rt79G9XD7/crJOZHHoxCGO5Vfsk7fk+iVc1Oki8/0fS3hu5XNld3aCD80Ia9pFtKtQ+KRnpnPwxEG78eSczCn93qZtlc55euwlGgY1JCQohAAVQIAKQNsCOZEbQNMmgRUuv4cEhdA1qiuBKpDgwGCCA4IJCgiiYVBDggOCaRLSpHTfAW0HMCF+AqHBoYQGhRLeIJzw4HAaNWhU2ipUYv349TRu2JhGDRqZ82szSmryQBhbrkhuFtqMZqHNqnxO5flrTrGyxcfSPj5KqSnA5NM2Pwm8C2wGemitdyulpgE3AI2ATOBD4GmtdUFN50hISNCpqamWxexLUlLgqyVHOd76G462XFKpFQdg822b6d6iOwAvr3qZ/x3+g+aFfcj5PY4tP/RmzYrGdOtmhoGWzKbqbdO/C8/iyPV4b8kpt94KffqYIdquUFAAnTubxUv796/fMQqLCglUgaXDnF9JeYXF2xazI3sHu3J2mbyxZwDsTKT/4JOsnvIKAAdPHKTFSy1KjxOgAmgWYv5xN2nYhJcvepkLYi8ATOGzbPtyvvgknE7twrl0RCihwaGEBIXQNKQpI7uUdVT6Zb9ZryE4IJjgQFN4BAUEEagCaRrStLRQKbAVkFeYR4AKIFAFmq8Bgaji6S9qGrY9a5bpI7V6teNz59TVggVmSoK0NMmrdVVUZOYIKiyEwEDH+vg4pXOzM0nhYxLW1oNbSzsbd2jagfEJ4wHzqSnurbgK+3do2oG4Vmb5hlv73QpH25Yu8LlsmZlLY9gwU+gMGeJdU70Lz2dF52ZncjSnaG2a/7/7Drp2tTCwGrzxBnz7rflnWpOs3Cx+zfiV9RnrSc9MZ8OBDWw5uIVNt22ic6SZSOvmBTcze/3s0sdEhUbRrkk72kW0o3+b/kw6fxJgWlTW7F1Di/AWRIVG0SSkSbVzbM2aZWJds8a6ZTwcNXGimT/n229NC7krHD1qWszfe8+5lyh9WXi46VTdqJEUPn7h002fsvCPhaRlmFacU7ZTpfdd0P4CksckA6aT3t2L7jazG7cyI6o4FUFyclmhc+CA6bRYUux06OCe5yScz1kj/erC1wufjRvN5Ytt21x7GTgvDzp2hCVLTGtTCa11aavH74d+56IPLmJXjv1Ra4uvW8zwzsMBWLtvLZm5mXRo2oHYprHV9jWprX37zCi05csrxuhuNpsZIdSkCcye7Zrf2y23mPO8847zz+VM7swpLVrApk0QHe2Fo7pEZYVFhaYvTkZaaWfjVy9+lS5RXQD4bsd3FT6NdWzWkT7RfejTsg/925a1dTcIbMCrw99kzRr4dhY8uNR0uuzf3xQ6H35ohpP6wsyvonqyXIdrLFninjW0QkPhvvvg6efyufOF1Xy34zuSdybTPKx5aafdthFt2Xt0L+HB4fRt1ZezWp1FXKs4erfsTY8WPSr0czm7jbUTEGkNt98O//ynZxU9YPpJffSRaeGePNmsheZMCxaYzuhpac49j7O5O6dY1c9HCh83Opx3mPu/vZ/0zHQ2HdhUoRUHYN3+daWFzzW9rzGFTvFK4+XXW9HadEJeutTcfvwROnUyrTlTpphOl6E1TfYvfI4s1+Eay5bBuHGuPefeo3v5cuuXLG+1kCWdk/lsdtlwl6jQqNJWn7DgMLbcsYUOTTsQGGDxOho1+PxzswDn/PkuPW2thYXBV1+Zv4mYGNNPyxkOHDDD+D/5xHQr8GbuzilWjeySwseJyrfilPTHiWgYwbwr5gHQqEEjPkz/kMIiM0ClQ9MOpcVNXHQc57UvW+nw/Pbnc377smEAGRkm4ZbcAgNNoXPddfDuu6ZJUPg3mUfI+Ww2WLUKPvjAuefRWlNQVECDQNMhZf7G+Tyw9AFzZzA0OdWDm84bxpAOQzgv5rwKHXxL+vC4Una26eg9f75nd+Jt2RIWLTJ/G40bm1merVRQYI55883WL1zrDu7OKdLi42HKX1efs34Or/78qt1WnGYhzUr3bRDYgPcve5+YJjGVWnFOl5trWnJK+uns2WPedElJZkKzzp1lmLmoyBPm/PB1aWnQtq31K4CX2HpwK3M3zOWTTZ9wTa9rmJxoBrhd0vUSUvamMLLLSAZFD+e8uDbccTN06eKcOOpq4kTT72mwFyxD3bWrmXzyootMy/ill1p37HvuMa0U7pj3xhncnVOkxcdN7LXipGemM334dK7seSUAuQW5pUMzY5vGEhdtRlSVtOaUd03va+yex2Yza9qUjL5KTYX4eNNP5//+z3wfJL89UQN/nfPDVX780fpJC7Pzsvlow0fMSZvD2j/Xlm5fvmN5aeFzZvMzS/vxANx5p5nX5z1rl2mqlx9+MIXExo3ujqT2+vSBr782y4DMmGEmiXTUm2+afj0pKaZF3le4M6dIi48LHDt1rLTzn9aaQe8O4tf9v1ZqxQHYkLmhtPC5rNtlpi9Oy94VJr6qjtZmVEhJP53vvzefJJOSzKen886DRo2se25CCMetWGFGB1nlX6v/xSPLH+FkoVmNsXGDxlzR4wqu7X0tibGJVT7urrtMa8/WrXDmmdbFU1cnT5r+Tq+9ZkZMeZOEBDO8/S9/MV0J7rij/sd6+2149lnTMuJtr4MnCwuTwscy9lpx0jLTyCvI49DEQyilUEqRm5/LKdup0lac3i17l86P0ymyU+nxWjduTevGrWs878GDptmwpFWnoMC06Fx+uZn34owznPmshRCO0NoUPv/6V/2PcbLwJDknc4huFA1Al8gunCw8ybCOw/hH339wWbfLCA2ueWRC06Zw//1mhNK8efWPx1HPPAO9erluLS6r9e0LK1eaUXpbt8KLL9Z9YMjLL8Prr5uWr06dat5f1J5c6qqnw3mHsRXZaBFuev9+sukTbvziRrutOGHBYWSdyKJleEsAPrvyM6LDo2vdinO6vDzzR1XST2fbNtNMnpQE994L3btLPx0hvMXWrabpvV27uj/2cN5h3vj5DV5f+zqJsYnMv8IMfbq488Vsv2s7HZrVfXKtO+80rT6//mqmrHC1tDSzeOX69a4/t5U6dDCzOk+YAGefDXPnQlxczY87eNC0vK1fby6B1ud9Iaonl7pqUNKKk56ZXtaKk5HGvmP7eHTwozw79FkA2jRuU9qKUzKaqqQ/TqfIThVmJO0aVbdpWYuKTBIqGXm1erW5lpyUBK++aubW8ZSZTIUQdbNiRd1H6mQcz2Daqmm8ve5tjucfB2B79nYKbAUEBwYTGBBYr6IHzD+FRx+Fxx6Db76p1yHqraDAjFx64QVoXXNjt8dr1sy0nH34YdlErw8/bH8+opwcs++UKXDttWaCwrAwl4fsF6TFp5xDJw6x8cBGzm9/funIqgHvDGDd/nWV9g0LDiu9fg5wTptzOPLQkXq34pxu586yFp3ly82w8qQk80ngP/+BiKoHbgkhvEhdOjZn5WYxdeVU3kx9szT/DO80nInnTmRI7JAa15eqrbFjzaWWklE3rjJtmsl1Y8a47pzOphTccAOMHg1vvQXDh5v83b8/tG8PR46Y0bXff28m9fv8cxlI4Gx+2+JzsvAk8zfOL+2HU9KKA7Dn3j20jWgLQPcW3Tl44iBxreLo07JP6RIOnZp1qjCRV3BgME0C61/0ZGebNXpK+ukcO2Y+IYwYYZKBNHcK4ZtWrDCtK7Vx5OQRXl3zKjZt47Jul/H4+Y/T74x+lsfUsKHpl3L33WZUqCtGfm7aBNOnm5GnvnipPiLCDDC5/37YvNmsObZ3r7mseO65Zt40Wd/QNcLCzP9cR3ld4bPpwCau/s/VFbaFBYfRq2UvsvOySwuf2aNnlxY4KSmQ/CW0TYSuDlbkp06ZCctKLl/99pt58w8bZqZm79Wr5uUgPGH9JCFE/X35JWRlwaFD9u8vsBXw3y3/5YoeV6CUoktUF14f+Tr92/TnrDOs74BTPqdccYUZkj1zJtx2m+WnquDUKTNp6vPPm1YQXxYYaBYZ7d3b3ZH4r/Bws/6bo7yu8GkQ1ICLz7yYPi1NC06f6D6VWnGACkWPI2uLaA0bNpS16Pz0k+mEnJRk/tgHDarbzKTuXutECOGYlBT4+9/N3/CwYZX/hr/d9i13L76bLQe38PmVn/PX7n8FYELCBKfFc3pOefVVs+2qqyAqyimnBeCJJ0xn4H/8w3nnEKKE3/bx6d2yNwuuXlDr/euztsjevWWFzrJlZirzpCSzlstHH5mObyXq2nrj7rVOvIm0jAlPlJxsOvNCxb/hXUd2ce+Se/liyxeAWSqiPiucW5FTHnnEFD0PP2wmPHWG5GSzVEdamvdc4pKc4t38to9PXdVmbZGcHPPHsHy5KXaysuDCC02x88wz5hONPfVpvXH3WifeQlrGhKdKTDT/6JUy783B5xcybdW/mJw8mRMFJwgPDueJC57gngH3lK6tVVtW5pRnnjHDsBctMn0OrfTnn+YS13vvec+6gJJTvJ/ftvjUlb21RQoKTAe1klmS09NhwABT6Hz4oZkDo6Z+OlC/1ht3r3XiLaRlTHiqc86BkBC47z6zxMEa9ToPLnkQgCt7Xsn0i6bTJqJNvY5tZU5p0sQUJtdfb3KcVZe88vPNpb4JE8xIJ28hOcX7SYtPHQwYYJLAsmVmPZsffzQzag4bBk8+aRbSq+vsnFD/1htZP6lm0jImPNVvv0GbNmULT/YtGM/Xv3/NfQPvY2SXkQ4d2+qcMmSIueR1221mrhlHL0lpbQq+qCizOLI3kZzi/TyyxUcpdQcwBugNfKy1HlPNvvcCDwGhwH+Af2qtK0+fXE8ZGWUjr5YuNcM6k5LMp59337WmeVZab5xHXlsBnpVTSvz3p83kjZ7E0VNziGgYQWhwKMtuXGbJsZ3xvn/2WTMI48UX4aGHHDvW88+b2FaurF2ruCeRnOL9PLXF50/gGWA4JvnYpZQaDjwMXFj8mC+AJ4u31UturlkbpaTQ2bvXfNpJSjKfTDp3dk4HPGm9cR55bQVuzCmn01rz+s+vM2X/RGyNTvL0D0/z0kUvWXX4Ula/70NDzcrjAwdCbKxpAaqPN980sxKvWGHWBvNGklO8m0e2+GitPwdQSiUAbavZ9SZgltZ6U/H+TwNzqUOSKiw0E3SVjLxatw769TOFzjvvQHy8aybvEkI4jytzSnUOnTjEzQtu5qvfvwIFl7S5mccveNyKQ7tEmzbw1Vfm8n5kpMmTtaW1WW39xRdNNwFfWJJCeCdPbfGprZ5A+THpaUC0UipKa11pSjCl1DhgHEBk5JlcfrmZJrxtW/MH/NBDZs2cRo1cE7zwLjKE1S/UO6fExMRUe+CUPSlc+dmV7D26lyYNm5A3/x0+W31Fnebv8gRxcWbZnCuvNPPv1GZyw1OnzH5r15qWnqpGuPobySnu4ZEtPnXQCMgp93PJ942BSklKaz0TmAnQvHmCvvxyMzNpq1ZOj1N4ORnC6jfqnVMSEhJ0VQf9/dDvnD/7fAqLChnQdgD3tvuYaZ/Hel3RU+L8880krKNGwc8/w1NPgb26T2tYssR8qOzUycxWLx8sDckp7uPthc9xoPxynSXfH6vpgbGxpoOyELUhQ1j9Rr1zSnW6RnVlbL+xhASF8MKwF3jt38Gcc44jR3S/Tp1g9WrT6fmss+DSS+GCC6BjR/M3snatWd390CEzF9Dll3vPBIWuIDnFfYKDzdIhRUWOHcddhc8mIA74pPjnOCDTXpO0EI6QIax+w7KcsjtnN7n5uXRv0R2AN0a+Ubp6+i+/mE/73i4iAl54wbTovPOO6Se5fbvpF3nOOWZBzlGjpJ+kPZJT3CsszEw67Airh7MHFR8zEAhUSoUAhVrrwtN2fR+YrZSaC+wHHgNmWxmLqDtfvG4tQ1i9m6tzSsqeFEbPG01Ewwh+HvszkaGRpUUPmEEUEyfW88l4oMhI5z8fX8srklPcKzzcwwofTLKZXO7n64EnlVLvApuBHlrr3VrrxUqpF4HvKZtzY3Klo3kxb/tj9+Xr1jKE1au5LKfM2ziPMf8dwynbKeJaxVW6//hx2LXLLFLsDt6WU8B384rkFPcJC3P8GFYPZ58CTKni7gpd47TW04HpVp7fU3jjH7tctxaeyFU5ZeqKqTz63aMATIifwGsjXyMooGJ6TEuDXr1MPwNX88acApJXhPXC677ubyVeNvemd7D3x+7pSq5bBwbKdWvhX3bn7ObR7x5FoZh+0XRm/GVGpaIHTP+efv3cECDemVNA8oqwnse1+AjDGzu/yXVr4a+ycrNoGNiQuZfP5W89/lblfuvWwbnnujCwcrwxp4DkFWE9K1p8lNZVTmHhkRISEnRqaqq7w6iRN16PF8IZlFLrtNYJ7o6jKm27tdUfL/mY89qfV+1+ffqY1c7j410U2GkkpwgBixfDiBGO5RQpfIQQTuXphU9tckpenlmRPDsbr528UAhf4WhOkT4+QghRgw0b4MwzpegRwhdI4SOEEDX45Rf3XeISQlhLCh8hhKjBunXuG9ElhLCWFD5CCFGDX34x61oJIbyfFD5CCFGNggL47TczqksI4f2k8BFCiGps3QoxMdbMHyKEcD8pfIQQohrr10Pfvu6OQghhFSl8hBCiGlL4COFbpPDxcikpMHWq+SqEsN769RBXebF2nyU5Rfg6WavLi3nris1CeAut/avFR3KK8AfS4uPFvHXFZiG8xZ9/mpXFW7VydySuITlF+AMpfLxYyYrNgYHetWKzEN6ipLVHKXdH4hqSU4Q/kEtdXmzgQNMULSs2C+Ec/ta/R3KK8AeWt/gopSKVUl8opXKVUruUUtdWsd8YpZRNKXW83C3R6nh83cCB8MgjkqCE73JnTvGn/j0lJKcIX+eMS11vAPlANHAd8KZSqmcV+6ZorRuVuyU7IR4hhHdzW05JS/O/wkcIX2dp4aOUCgf+BjyutT6utV4JfAncYOV5hBD+wZ055dgx2LsXunZ19pmEEK5kdYtPV8Cmtf693LY0oKpPZ2cppQ4qpX5XSj2ulLLb50gpNU4plaqUSs3KyrI4ZCGEB3NbTtmwAXr0gCDpCSmET7G68GkE5Jy2LQdobGffH4FeQEvMJ7prgAftHVRrPVNrnaC1TmjRooWF4QohPJzbcopc5hLCN1ld+BwHIk7bFgEcO31HrfV2rfUOrXWR1noD8BRwhcXxCCG8m9tySlqaf43oEsJfWF34/A4EKaW6lNsWB2yqxWM14CezZQghasltOUUKHyF8k6WFj9Y6F/gceEopFa6UOhcYDXxw+r5KqRFKqeji77sBjwMLrIxHCOHd3JVTiopMH58+feofuxDCMzljOPttQChwAPgY+KfWepNSKqZ4Xo2Y4v2GAulKqVxgISa5PeeEeIQQ3s3lOWXbNoiKgqZNHQ9eCOFZLB+voLU+DFxmZ/tuTEfFkp8fAB6w+vxCCN/ijpwil7mE8F2yVpcQQpxGCh8hfJcUPkIIcRopfITwXVL4CCHEaaTwEcJ3SeEjhBDlHDkChw9Dp07ujkQI4QxeX/ikpMDUqearEEI46qOPoFkzWLPG3ZEIIZzBq1ehSUmBoUMhPx8aNIDly2HgQHdHJYTwVikpcM89UFhocovkFCF8j1e3+CQnm6LHZjNfk5PdHZEQwpslJ5uiR2vJKUL4Kq8ufBITTUtPYKD5mpjo7oiEEN6sJIcEBEhOEcJXefWlroEDTVN0crJJUNIkLYRwxNlnQ3AwPPIIDB8uOUUIX+TVhQ+YxCTJSQhhha1boX17mDLF3ZEIIZzFqy91CSGElWT+HiF8nxQ+QghRbP166NvX3VEIIZxJCh8hhCgmLT5C+D4pfIQQAjOE/ddfpcVHCF8nhY8QQgAZGWZOsDZt3B2JEMKZpPARQgjMZa6+fUEpd0cihHAmKXyEEALTsVn69wjh+6TwEUIIylp8hBC+zfLCRykVqZT6QimVq5TapZS6tpp971VKZSilcpRS7yqlGlodjxDCu7kqp0iLjxD+wRktPm8A+UA0cB3wplKq5+k7KaWGAw8DQ4FYoCPwpBPiEUJ4N6fnlNxc2LULune3KmQhhKeytPBRSoUDfwMe11of11qvBL4EbrCz+03ALK31Jq11NvA0MMbKeIQQ3s1VOSU93RQ9DRpYFLgQwmNZvVZXV8Cmtf693LY04AI7+/YEFpy2X7RSKkprfaj8jkqpccC44h9PKaU2WhizlZoDB90dRDU8OT5Pjg08Oz5Pjg3gTAce65KcMmiQySkeOqLLk3+/Elv9eXJ8nhwbOJZTLC98GgE5p23LARrXYt+S7xsDFZKU1nomMBNAKZWqtU6wJFqLeXJs4NnxeXJs4NnxeXJsYOJz4OF+nVPAs+OT2OrPk+Pz5NjA4ZxieR+f40DEadsigGO12Lfke3v7CiH8k+QUIYSlrC58fgeClFJdym2LAzbZ2XdT8X3l98s8vUlaCOHXJKcIISxlaeGjtc4FPgeeUkqFK6XOBUYDH9jZ/X3gFqVUD6VUM+AxYHYtTjPTqnidwJNjA8+Oz5NjA8+Oz5NjAwfik5wCeHZ8Elv9eXJ8nhwbOBif0lpbFYg5oFKRwLtAEua6+sNa64+UUjHAZqCH1np38b73AQ8BocB/gAla61OWBiSE8GqSU4QQVrK88BFCCCGE8FSyZIUQQggh/IYUPkIIIYTwGx5X+Hj6Wl+1jU8pNUYpZVNKHS93S3RybHcopVKVUqeUUrNr2Nelr11tY3PT69ZQKTWr+Pd5TCn1q1JqRDX7u+y1q0ts7njtis/7oVJqv1LqqFLqd6XUrdXs67F/s54en+SU+sUmOcWx+Nz0+jk3p2itPeoGfAzMx0xGNhgzCVlPO/sNBzIxs7U2A5KB5z0ovjHAShe/dpcDlwFvArOr2c/lr10dYnPH6xYOTMGs7xQAXIKZ+yXW3a9dHWNz+WtXfN6eQMPi77sBGUC8u1+7cueVnFL/2CSn1C82j80p9YjPHa+fU3OKy55IHX4Z+UDXcts+sPdEgI+A58r9PBTI8KD4XP5mKXfuZ2pIBC5/7eoQm9tet9PiSAf+5kmvXS1ic/trh5lKfj9wpSe8dpJTLItTcorjcXpsTqkhPre+fs7IKZ52qauqdXkqrcRcvC3ttP2ilVJRHhIfwFlKqYPFTXWPK6WsXiKkvtzx2tWFW183pVQ05ndtb5I8t752NcQGbnrtlFIzlFIngC2YJLXQzm6e/jfr6fGB5JT6kpxSDU/MK87MKZ5W+Fi1Lo+z1CW+H4FeQEvM6tLXAA86Mba6cMdrV1tufd2UUsHAXGCO1nqLnV3c9trVIja3vXZa69swr8F5mAkH7c2d4+l/s54en+SU+pGcUg1PzSvOzCmeVvh4+ro8tY5Pa71da71Da12ktd4APAVc4cTY6sJj1zRy5+umlArAXGbIB+6oYje3vHa1ic3d7zmttU1rvRJoC/zTzi4e/TdrZ1+Pis/dv98aSE6xw5NzCnh+XnFWTvG0wsfT1+WpS3yn04BySlR1501rGrnkdVNKKWAWEI25zl1Qxa4uf+3qENvp3PWeCwI62dnu6X+znh7f6SSn1I/f55Q6xnc6d7zvrM0p7uqwVE1HpnmYUQ7hwLlUPcLhYkxP7x6Y3tzf4ZoRGLWNbwQQXfx9N2AjMNnJsQUBIcBUTBUfAgR5wmtXh9hc/roVn+stYDXQqIb93PHa1TY2d7znWgJXY5qcAzGjLHKB0Z7w2hWfV3JK/WOTnFL/+Dw2p9QxPpe+fq7IKU59Yev5pCOB/xY/0d3AtcXbYzDNWjHl9r0PM5TtKPAexcPfPCE+YFpxbLnAdkzzYLCTY5uCqcbL36Z4wmtX29jc9Lq1L47nZHEsJbfr3P3a1SU2N712LYAfgCPFr8cGYKy9vwl3vO+Kzyk5pf6xSU6pX2wem1PqGp+rXz9X5BRZq0sIIYQQfsPT+vgIIYQQQjiNFD5CCCGE8BtS+AghhBDCb0jhI4QQQgi/IYWPEEIIIfyGFD5CCCGE8BtS+AghhBDCb0jhI4QQQgi/IYWPEEIIIfyGFD7CJZRSoUqpvUqp3Uqphqfd945SyqaUutpd8QkhvI/kFVEfUvgIl9Ba5wGTgXbAbSXblVJTgVuAO7XW89wUnhDCC0leEfUha3UJl1FKBQJpmNV3OwK3Aq9gVvp9yp2xCSG8k+QVUVdS+AiXUkpdAnwFLAcuBF7XWt/l3qiEEN5M8oqoC7nUJVxKa/018AswFJgP3H36Pkqp25VSPyulTiqlkl0cohDCy0heEXUR5O4AhH9RSl0J9C3+8Zi23+S4H3geOBsY6KLQhBBeSvKKqAspfITLKKUuAj4AvgAKgH8opV7RWv9Wfj+t9efF+8e4PkohhDeRvCLqSi51CZdQSvUHPgd+Aq4DHgOKgKnujEsI4b0kr4j6kMJHOJ1SqjvwDfA7cJnW+pTWehswCxitlDrXrQEKIbyO5BVRX1L4CKcqblb+FsgBRmitj5a7+ykgD3jRHbEJIbyT5BXhCOnjI5xKa70bM7mYvfv2A2GujUgI4e0krwhHSOEjPI5SKgjz3gwCApRSIUCR1jrfvZEJIbyV5BVRQgof4Ykew0xDXyIP+AFIdEs0QghfIHlFADJzsxBCCCH8iHRuFkIIIYTfkMJHCCGEEH5DCh8hhBBC+A0pfIQQQgjhN6TwEUIIIYTfkMJHCCGEEH5DCh8hhBBC+I3/B4kXc6vvVxn0AAAAAElFTkSuQmCC)]

Lasso回归子梯度向量：
$$
g(\Theta,J) = \nabla_{\Theta}MSE(\Theta)+\alpha\left|
\begin{matrix}
sin(\Theta_1)\
sin(\Theta_2)\
\vdots\
sin(\Theta_n)
\end{matrix}
\right|\ \ \ 其中sign(\Theta_i) =
\begin{cases}
-1\ 如果\Theta_i<0\
0\ 如果\Theta_i = 0\
+1\ 如果\Theta_i>0

\end{cases}
$$

from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
1
2
3
4

弹性网络

from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5, random_state=42)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
1
2
3
4

提前停止

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GFuvg0wm-1658889211622)(data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAABEYElEQVR4nO3dd3hUVfrA8e+bBEIJoYZA6ApSBQSsKCCgKAgWFAurgCIqYMdeALGsruju/tZVRBAUV7EAKq6yiIAiNQhBKaJI7016SXl/f5yZzEyYhASSmUnyfp7nPHPvuWfmnrmEvDnnnnuOqCrGGGNMpIkKdwWMMcaYYCxAGWOMiUgWoIwxxkQkC1DGGGMikgUoY4wxESkm3BXIT1WqVNG6deuGuxrGGGPyYPHixbtUNSFrfpEKUHXr1iU5OTnc1TDGGJMHIrI+WL518RljjIlIFqCMMcZEJAtQxhhjIpIFKGOMMRHJApQxxpiIVKRG8Rlj8l9GRgabNm3i0KFD4a6KKYRKlChB1apViY+Pz/N7LUAZY3K0a9cuRISGDRsSFWWdLib3VJUjR46wefNmgDwHKftp83jtNbj2WmjcGFasCHdtjIkcf/75J4mJiRacTJ6JCGXKlKFGjRrs2LEjz++3FpTH9OnwzTdue8UKaNIkvPUxJlKkp6dTokSJcFfDFGKlS5cmNTU1z++zP4k8Gjf2ba9cGb56GBOJRCTcVTCF2Kn+/FiA8rAAZYwxkcUClEejRr7tVavCVw9jjDGOBSgP/xbUqlWQkRG+uhhjwm/YsGE0a9Ys2/1gBg8eTIcOHfL93MWVBSiPKlVcAjhyBDZsCG99jDGnpnv37nTu3DnosZUrVyIiTJ8+Pc+fO2TIEGbPnn261Quwbt06ROSEVRgK4lwFoUOHDgwePLjAPt8ClJ+srShjTOHTv39/vvvuO9atW3fCsTFjxlCnTh06deqU58+Ni4ujcuXK+VDDyDpXJLMA5cf/PpQNlDCmcOrWrRuJiYm8++67Afmpqam8//773H777agqd9xxB/Xq1aN06dI0aNCAV155hYwc+vazdrulp6czZMgQKlasSMWKFXnggQdIT08PeM8333zDJZdcQsWKFalUqRJdunRhpd8vl3r16gFw7rnnIiKZ3YNZz5WRkcGIESOoVasWsbGxnH322Xz++eeZx70tsc8++4zLLruMMmXK0KRJk5O2FL///nsuuOAC4uLiKF++POeffz6//PJL5vG5c+fSvn37zGeZ7rnnHvbv3w9A3759mT17Nm+88QYigogE/aPgdFiA8mMj+Yw5OZHwpdyIiYmhT58+jBs3LiDgfPnll+zatYt+/fqRkZFBjRo1+Pjjj1m5ciUvvPACL7744glBLScjR45k9OjRjBo1innz5pGens4HH3wQUObQoUM88MADLFy4kFmzZlG+fHm6d+/O8ePHAVi4cCHgAtnWrVuZNGlS0HP94x//4G9/+xsvv/wyP//8M9deey3XXXcdS5cuDSj31FNPcd9995GSksK5557LTTfdxMGDB4N+ZlpaGldffTUXX3wxKSkpLFiwgPvvv5/o6GgAfv75Zy6//HJ69OhBSkoKkyZNYunSpdx+++2Zdbrwwgvp168fW7duZevWrdSqVSvX1y9XVLXIpNatW+vp+PprVXDpkktO66OMKTJWrFgRsO/9PxKOlFurV69WQKdNm5aZ17VrV73iiiuyfc9jjz2mnTp1ytwfOnSoNm3aNNv96tWr6/PPP5+5n56erg0aNND27dtne46DBw9qVFSU/vDDD6qqunbtWgV00aJFAeWynispKUmHDx8eUKZ9+/bau3fvgM956623Mo9v2rRJgcxzZbV7924FdNasWUGP33rrrXr77bcH5C1ZskQB3b59e2YdBg0alO339Zf158gfkKxBfqdbC8qPdfEZUzQ0aNCAdu3aMXbsWAC2bNnCtGnT6N+/f2aZt956izZt2pCQkEBcXByvv/46G3I5Omrfvn1s3bqVCy+8MDMvKiqK888/P6DcmjVruOWWWzjzzDOJj48nMTGRjIyMXJ8HYP/+/WzZsoW2bdsG5F988cWsyDIvW/PmzTO3k5KSALKdYqhSpUr07duXLl260K1bN1577TU2btyYeXzx4sVMmDCBuLi4zOStw5o1a3Jd/9NhAcpP7dpQpozb3rXLJWNMoHC2ofKif//+TJkyhT179jBu3DgqVapEjx49AJg4cSIPPPAAffv2Zdq0aSxdupSBAwdmdr3ll+7du7Nz505GjRrFggULWLJkCTExMad0nmCzMWTN85+Synssp/tq7777LgsWLKBdu3Z88cUXnHXWWUybNi3zff3792fp0qWZKSUlhd9++42WLVvmuf6nwgKUn6goaNjQt2+tKGMKr+uvv55SpUoxYcIExo4dy2233Zb5C3zOnDmcf/75DB48mFatWlG/fv08tQrKly9P9erVmT9/fmaeqmbeUwLYvXs3K1eu5Mknn6Rz5840btyYAwcOkJaWllmmZMmSACcMrvAXHx9PUlISc+bMCcifM2cOTfJh0tAWLVrw2GOPMWvWLDp06MD48eMBaNWqFcuXL6d+/fonpNKlS2fWP6e6ny4LUFnYjBLGFA2lS5fmlltuYdiwYaxZs4Y77rgj89hZZ53FTz/9xNdff81vv/3GiBEj8vzc0f33388rr7zCp59+yq+//soDDzzA1q1bM49XrFiRKlWqMHr0aH7//Xdmz57N3XffTUyMb47uqlWrUrp0aaZNm8b27dvZt29f0HM98sgjvPrqq3z44YesXr2aZ599lh9++IGHH344j1fFZ+3atTz++OPMnTuX9evXM3PmTJYtW5YZ9B577DEWLlzI3XffzZIlS/j999+ZOnUqd911V+Zn1K1bl4ULF7Ju3Tp27dqVY2vtVFiAysJG8hlTdPTv35+9e/dy0UUX0djvP/ddd91Fr169uOWWWzj33HNZt25dnn/ZP/zww/Tr14/+/ftz/vnnk5GRQe/evTOPR0VFMXHiRJYtW0azZs0YNGgQI0aMIDY2NrNMTEwM//znP3nnnXdISkri6quvDnqu++67j0ceeYRHH32UZs2aMXnyZD777LPT6morU6YMq1ev5oYbbuCss86iT58+9O7dm8ceewxw97O+//571q1bR/v27WnRogVPPPEEiYmJmZ8xZMgQSpYsSZMmTUhISMjTvbXcEM1rx24Ea9OmjWZ9IjuvPv0UbrjBbV9xBXz9dT5UzJhCbOXKlQG/3I05FTn9HInIYlVtkzXfWlBZ2GwSxhgTGSxAZVG/vhssAbB+PRw+HN76GGNMcWUBKovYWDjzTLetCr/+Gt76GGNMcRXSACUiE0Rkq4jsF5HVItI/m3J9RSRdRA76pQ6hqqd18xljTPiFugX1ElBXVeOBHsDzItI6m7LzVDXOL80KVSVtRgljjAm/kAYoVV2uqse8u550ZijrkBv+LagsM4kYY4wJkZDfgxKRf4vIYWAVsBX4bzZFzxGRXZ6uwGdEJCZYIREZICLJIpK8c+fOfKnj2Wf7trNMFmyMMSZEQh6gVHUgUA64BJgEHAtS7HugGVAV6AncDDySzee9raptVLVNQkJCvtSxaVPwPuy9Zg1k83C3McaYAhSWUXyqmq6qc4CawD1Bjv+hqmtVNUNVfwaeA64PVf1KlQrs5lu2LFRnNsYY4xXuYeYx5O4elAK5XK7sNHlWizznHF/WkiUhObMxJoL17duXq666Kk/v6dChA4MHDy6gGhV9IQtQIlJVRG4SkTgRiRaRLriuu++ClL1SRBI9242AZ4DPs5bLV4cOQZ06kJQE6ekWoIwppLzLj2eX+vbte0qf+49//IMJEybk6T2TJk3ipZdeOqXzhdKpBN9QCDrwoIAorjvvLVxgXA88oKqfi0htYAXQRFU3AJ2AcSISB2wHJgAvFmjtypZ1a0ofOgSrVnHOOU0zD1mAMqbw8J9RfOrUqdx5550Bed6lIrxSU1MD1lHKTvny5fNcl0qVKuX5PcYnZC0oVd2pqu1VtYKqxqvq2ao62nNsg+dZpw2e/SGqmqiqZVX1DFV9VlVTC7ySrT2PZC1ejP8kwcuXw7FgQzmMMRGnWrVqmalChQoBeUePHqVChQp8+OGHdOzYkdKlSzNq1Ch2797NzTffTM2aNSldujRNmzbl3XffDfjcrK2MDh06MHDgQJ588kmqVKlC1apVGTJkSMCSE1m7+OrWrcvzzz/PXXfdRXx8PDVr1uRvf/tbwHlWr15N+/btKVWqFA0bNuS///0vcXFxjBs3Ltvv/PPPP9OpUyfi4+MpV64cLVq0YObMmZnHV6xYQbdu3ShXrhxVq1bl5ptvZtu2bQAMGzaM8ePH89VXX2W2MmfNmpXXy14gwn0PKrK08Uymm5xM+fJwxhluNy3NnocyJoBI9untt33l3n4757L+WrfOXbl88MQTTzBw4EBWrFjBNddcw9GjR2nVqhVTp05l+fLl3H///dx1113MmDEjx8/54IMPiImJYe7cufzrX//i73//OxMnTszxPa+//jpnn302P/30E4899hiPPvoo8+bNA9wqttdeey0xMTHMnz+fcePGMXz4cI6d5C/kW265herVq7Nw4UKWLFnCsGHDKFWqFOBalO3ataNZs2YsXLiQb7/9loMHD9KjRw8yMjIYMmQIvXr1onPnzmzdupWtW7dy0UUX5eFqFpxQdvFFPr8WFLiBEn/84bKWLAkcOGGMKbzuvfderr8+cGDwI4/4nmQZMGAA3333HR9++CGdOnXK9nOaNGnCc889B7hFEEePHs2MGTO4+eabs33P5Zdfntmquvfee/nnP//JjBkzuPDCC5k+fTq//vor//vf/6hRowbgAlrbtm1z/D7r169nyJAhNPJMg1O/fv3MY2+++SYtWrTg5Zdfzsx77733qFSpEsnJyZx33nmULl2a2NhYqlWrluN5Qs1aUP68AWrJEkhLs4ESxmRHNfs0YICv3IABOZf1t3hx7srlgzZtApceSk9P54UXXqB58+ZUrlyZuLg4Jk2adNIF+Jo3bx6wn5SUxI4dO075PatWrSIpKSkzOAGce+65REXl/Kv6oYceon///nTs2JEXXniBVX6TiC5evJjvv/+euLi4zFSrVi2APC1zHw4WoPxVrgz16sGRI7BqFa1a+Q4tWhS+ahlj8lfZsmUD9l999VVGjhzJI488wowZM1i6dCnXXHMNx48fz/Fzsg6uEJGTLnue03tUFTmFLs1hw4ZldlfOnTuX5s2bM3bsWMB1G3br1o2lS5cGpN9++y0iR+75sy6+rEaOhLg4qFeP86r7spcscQMl/FZrNsYUEXPmzKF79+7ceuutgAsUq1evzhxkESqNGzdm8+bNbNmyhaSkJACSk5NPGvQAGjRoQIMGDbjvvvu45557eOedd7j99ttp1aoVH3/8MXXq1Ml2tGLJkiVJT0/P1++SH6wFldW118Jll0HZslSuDA0auOzjx62bz5ii6qyzzmLGjBnMmTOHVatWMXjwYNauXRvyelx22WU0bNiQPn36kJKSwvz583nooYeIiYnJtmV15MgRBg0axKxZs1i3bh0LFixgzpw5NGnSBIBBgwaxb98+brzxRhYsWMAff/zBt99+y4ABAzhw4ADgRhf+8ssv/Prrr+zatYvU1IIfNJ0bFqBO4oILfNvz54evHsaYgvP0009z3nnnceWVV9KuXTvKli1L7969Q16PqKgoJk+ezLFjxzjvvPPo06cPTz31FCKSOSovq+joaPbu3UufPn1o2LAh1157LRdeeCGvvfYa4O5x/fjjj0RFRXHFFVfQtGlTBg0aRGxsLLGeLqE777yTxo0b06ZNGxISEvjxxx9D9p1zIloANyDDpU2bNpqcnHx6H6IKr7zimksTJvDvt2MYNMgduvFG+Oij06+nMYXJypUraew/OaUJqZSUFFq2bElycjKtW2e3fF7ky+nnSEQWq2qbrPl2DyorERg92k1j/uSTXHCBb8SNtaCMMQVt8uTJlC1blgYNGrBu3ToeeughWrRoQSv/UVvFhHXxBeP9KyU5mbPPBu/MKOvXg+fha2OMKRAHDhxg8ODBNGnShN69e9O4cWOmTZt2SqP7CjsLUMF4n5FYvJgSJXzxCmDBgvBUyRhTPNx2222sXr2aI0eOsGXLFv7zn/+QmJgY7mqFhQWoYPxaUGADJYwxJhwsQAXj7etNSYHU1IAANWdOeKpkTDgVpcFUJvRO9efHAlQwFSpA/fruydzly7n4Yt+hhQvdRBPGFBfR0dER81yMKZyOHDmSqyVNsrIAlZ1u3dxDu0BiInjmYOT4cevmM8VLhQoV2L59e65mMzDGn6py+PBhNm/eTNWqVfP8fhtmnp2//z1gt3178M6/OHs2XHpp6KtkTDhUqVKFTZs28euvv4a7KqYQKlGiBImJicTHx+f5vRagcql9exg1ym3Pnh3euhgTSlFRUdSuXTvc1TDFkHXx5WTvXpgxA44fp317X/b8+bbCrjHGFDQLUDm58ELo3Bl++YWkJDduAuDoUVt+wxhjCpoFqJx4n4fyRCP/VpR18xljTMGyAJWTc891r57pI/wD1HffhaE+xhhTjFiAyknbtu7V83Rup06+Q3PmwOHDYaiTMcYUExagcnLOOVC2LPz2G2zbRlISNG3qDh0/Dt9/H97qGWNMUWYBKicxMb6J+DwLeF1+ue/w//4XhjoZY0wxEdIAJSITRGSriOwXkdUi0j+Hsg+KyDYR2SciY0UkNpR1zeSd5+iXXwALUMYYEyohXVFXRJoCv6vqMRFpBMwCuqnq4izlugDvAR2BLcBkYL6qPp7T5+fLirpZbd8OGRlQvTrg7jtVrOi6+AA2bYIaNfL3lMYYU5xkt6JuSFtQqrpcVb2PuKonnRmkaB9gjKf8XmAE0Dc0tcwiMTEzOAGUKQOXXOI7PH16GOpkjDHFQMjvQYnIv0XkMLAK2Ar8N0ixpkCK334KkCgilYN83gARSRaR5J07dxZInTN5Jsu87DJf1rRpBXtKY4wprkIeoFR1IFAOuASYBASbNCgO2Oe3790uF+Tz3lbVNqraJiEhIb+r63z4ITRoACNGAHDFFb5DX38NthKBMcbkv7CM4lPVdFWdA9QE7glS5CDgP/Wtd/tAQdctqNhY+P33zOehmjcH79yZ+/bBDz+EpVbGGFOkhXuYeQzB70EtB1r47bcAtqvq7pDUKivvA7vz5kFaGiLQvbvv8JdfhqVWxhhTpIUsQIlIVRG5SUTiRCTaM1LvZiDYpEHvAXeISBMRqQg8DYwLVV1PkJjouvgOHYKffgKgRw/f4c8/B1sR2xhj8lcoW1CK687bBOwFXgUeUNXPRaS2iBwUkdoAqvoN8AowE1jvSUNDWNcTeVconDEDcPPylfPcEVu7FlasCFO9jDGmiApZgFLVnaraXlUrqGq8qp6tqqM9xzaoapyqbvAr/5qqJnrK9vMbnh4e3on4PAEqNha6dPEdtm4+Y4zJX+G+B1V4eFtQP/7oFoQisJvviy/CUCdjjCnCbMn33EpIgNdfh2bNIDoagK5dISrKPR41f76bdCIxMcz1NMaYIsJaUHnxwANuhd0SJQCoXNk3wE/VDZYwxhiTPyxAnabrrvNtf/JJ+OphjDFFjQWovHrrLbjmGvjzTwCuv9536LvvYMeOsNTKGGOKHAtQefXBB64vb/ZsAGrW9K3IkZEBkyaFsW7GGFOEWIDKqyzDzQF69fIdnjgxxPUxxpgiygJUXnkDlN86G9dfDyJue/Zs2LYtDPUyxpgixgJUXl1wgZtCYtUqWLcOcMtFtWvnDqvCZ5+Fr3rGGFNUWIDKqxIlfOu+f/11ZvaNN/qKWDefMcacPgtQp6JrV/f61VeZWddd5x7aBbf8xvr1YaiXMcYUIRagTsWVV7pVC6+5JjMrMTFwpd333w99tYwxpiixAHUqqld33Xv9+wdk9+nj237vPVuCwxhjTocFqHx0zTUQ71n797ff3PqGxhhjTo0FqFOVkeHGlL/wQmZTqXTpwGeixo0LT9WMMaYosAB1qlTdyIinn3bNJQ//br6JE+HIkTDUzRhjigALUKcqOtoNlICA0Xxt28KZZ7rt/ftthnNjjDlVFqBOx1VXudcpUzKzROC223xFxo4NbZWMMaaosAB1Orp2dQ/uzpkDO3dmZvfp45v6aPp0WLMmTPUzxphCzALU6Shf3s3Nl5ERsOZ7nTruUSmvt98OQ92MMaaQswB1uq691r1OnhyQfffdvu1334Vjx0JYJ2OMKQIsQJ2uq6+G2rWhUaOA7K5doVYtt71z5wnxyxhjzElYgDpdiYluVvNXXw3Ijo4OnGhi1KjQVssYYwq7kAUoEYkVkTEisl5EDojIEhG5MpuyfUUkXUQO+qUOoaprnnlHRGRxxx0uUAHMmgUrV4auSsYYU9iFsgUVA2wE2gPlgWeAj0Wkbjbl56lqnF+aFZpqnqKdO92Y8qNHM7Nq1IAePXxF/vWvMNTLGGMKqZAFKFU9pKrDVHWdqmao6lRgLdA6VHUoUFde6ZpM//tfQPa99/q2x42DvXtDWy1jjCmschWgRORFESnjt99VREr77ceLyHt5ObGIJAJnAcuzKXKOiOwSkdUi8oyIxGTzOQNEJFlEknf6PYsUcjfc4F4//DAgu0MHaN7cbR8+DO+8E9pqGWNMYSWaizUhRCQdqK6qOzz7+4GWqvqHZz8R2KKq0bk6qUgJ4GtgjareFeT4GYAC64GmwETgfVV9KafPbdOmjSYnJ+emCvlv3TqoVw/KlIEdO6Bs2cxDY8e6xhW4AX9r1kBM0HBrjDHFj4gsVtU2WfNz28WXdRRA8FEBuatIFPA+cBwYHKyMqv6hqms9XYE/A88B15/qOUOibl244ALXTPryy4BDt9wCVaq47Q0bAmZGMsYYk42QDjMXEQHGAIlAT1VNzeVbldMIiiFz883u9aOPArJLlYJ77vHtv/56COtkjDGFVKifg3oTaAx0V9VsF6IQkSs93YaISCPciL/Inxf8hhsgKsqttvvnnwGH7rnHTdsHMHeum77PGGNM9vJyJ+RuETno9747RGS3Z7/cyd4sInWAu4BjwDbxPTt0F/ADsAJooqobgE7AOBGJA7YDE4AX81DX8KheHTp2dHPz7dgBFSoEHPrLX9y0RwAvvRSwSocxxpgscjtIYh2umy1HqlovH+p0ysI6SMIrLS3bERC//gqNG2cuwMvSpdCiReiqZowxkei0Bkmoal1VrXeylP/VLoRyGJ7XsCH07Onb/+tfQ1AfY4wppGwuvoKgCvPmwbRpJxx64gnf9scfw++/h7BexhhTiOT2Qd0WInJplrzeIvKHiOwQkbdEpGTBVLEQmj4dLroIHnjA15/n0aoVXH65287IgFdeCX31jDGmMMhtC+p54GLvjog0Ad4FfgM+BHoDj+V77QqrSy91s5yvWgULF55w+MknfdvjxsGmTaGrmjHGFBa5DVCtgOl++zcBK1S1i6reDzwA3JjPdSu8SpSA3r3d9vjxJxxu1w4uvNBtp6a6EX3GGGMC5TZAVQY2++23A/ynS5gF1M6nOhUNffq41w8/DJjhHNzqHM8+69sfPdrNlGTy17hx4xCRzBQdHU2NGjXo1asXv/76a4Gcc9asWQwbNoyMjIwC+fz8VLduXfr27Zvn9w0bNgzJZokZY/JTbgPUTqAGgIhE42YgX+B3vCQQ+f8jQ6l5c3fD6c8/4fMTnzHu0gXatnXbqakwYkRoq1ecfPLJJ8ybN4/vv/+el156iSVLltCpUyf27duX7+eaNWsWw4cPLxQByphIl9sANQsY6pnE9WFP3ky/402AdflXrSKiXz/3Onr0CYdE4IUXfPvjx8Pq1SGqVzHTsmVLLrjgAtq2bcttt93Gm2++yebNm5k7d264q2aMyUFuA9QzQAPgd+AF4FFVPeR3/FZgRj7XrfD7y1+gVi045xw3ZC+L9u2hc2e3nZ4Ow4eHuH7FVHx8PACpqYFTQaakpNCjRw8qVqxI6dKladu2LT/88ENAmUWLFnHZZZdRuXJlypQpwxlnnMHAgQMB1/U13POPWKJEicyuxZyICE8//TQjR46kTp06lC1blm7durFjxw527NhBr169KF++PLVq1eLll18+4f0LFy6kc+fOxMXFUbZsWTp16sTCIANz/vGPf1C3bl1KlSpFmzZtTvheXmvXrqV3794kJCQQGxtLy5YtmTx5co7fwZgCo6q5SrjpjVoASUGOtQAq5/azCiq1bt1aI056eo6H581TdWPRVUVUf/45RPUqBt59910FdNWqVZqamqpHjx7VFStWaKdOnbRq1aq6b9++zLKLFy/WMmXKaNu2bfWTTz7Rr776Srt3764lS5bU5ORkVVU9cOCAVqxYUbt06aJffPGFzpw5U99991298847VVV148aNescddyigc+bM0Xnz5um8efNyrCOgtWvX1q5du+rUqVN1zJgxWq5cOe3SpYtedNFFOmLECJ0+fboOGDBAAf3qq68y35uSkqKlSpXSVq1a6SeffKKffvqptmnTRkuVKqVLly7NLPfOO+8ooH379tWvv/5a/+///k9r1Kih8fHx2qdPn8xyGzZs0ISEBG3atKm+//77+s0332i/fv1URPTzzz/PLDd06FB1vzqMyR9AsgaLO8EyC2uKyACVC1dd5QtS3buHuzZFhzdAZU1JSUm6cOHCgLIdO3bURo0a6bFjxzLz0tLStFGjRnr11VerquqiRYsU0JSUlGzP6f3lnZqamqs6AtqgQYOA8g8++KACOmLEiMy81NRUTUhI0L59+2bm9ezZU8uXL6979+7NzNu3b59WrFhRr732WlVVTU9P15o1a2qXLl0CzvvRRx8pEBCgbr/9dq1SpYru2rUroGznzp21RYsWJ3xHY/JLdgEqtw/qPpSblD9tuiJo/354803473+DHh4xwt2TAreU1MyZQYuZUzR58mQWLVrEwoULmTJlCk2aNKFr166sXLkSgCNHjjB79mxuuOEGoqKiSEtLIy0tDVWlc+fOfP/99wA0aNCAChUqcNdddzFhwgQ2btyYL/W77LLLiPGbIqtRo0YAdOnSJTMvJiaG+vXrB5zz+++/56qrrqKC36TE8fHx9OjRg9mzZwOwadMmNm3aRK9evQLO2bNnz4BzAnzzzTd07dqV8uXLZ16DtLQ0unTpQkpKCvv378+X72tMbuV2NvNXgV3AQbJfl0mB1/KjUkXOxIkwcKAbtte16wmHW7aEW2+F995z+w8/DMnJbuUOc/qaNWtG/fr1M/cvv/xyatWqxbBhw5g4cSJ79uwhPT2dESNGMCKb4ZQZGRmUL1+emTNnMmLECAYOHMiBAwdo2rQpw4cPp6f/JIt5VLFixYD9kiVLZpt/1O+RhT179lC9evUTPq9atWrs3bsXgK1btwKQmJgYUCYmJobKlSsH5O3YsYP33nuP97w/iFns3r078/6dMaGQ2wCVjBup9xUwRlVtNaO8uPlmF3V+/BF+/hnOPvuEIi+8AJ98AkeOwJIl8P77vkepTP4qXbo0Z5xxBsuWLQOgQoUKREVFMWjQIG677bag74ny/LXQsmVLPvvsM9LS0khOTuall16iV69epKSk0KxZs5B9B4BKlSqxbdu2E/K3bdtGpUqVADID2Pbt2wPKpKWlsXv37oC8ypUrc8kll/DYY8EnhUlKSsqPahuTa7mdzfw84HxgLzBJRH4VkUe9iwqak4iLA+8vvrfeClqkZk0YMsS3/9RTbvV4k/8OHz7MmjVrSEhIAKBs2bJccsklpKSk0KpVK9q0aXNCyiomJoYLLriAESNGkJGRkdldGBsbC7huw4LWvn17vvrqKw4cOJCZd+DAAb788kvat28PQM2aNalVqxYff/xxwHu9QdbfFVdcwbJly2jatGnQa+D9bsaESq47kVR1uao+hHtg9ymgA7BORD4XEfvJPZm773av7713wmq7Xo8+CtWque3Nm2HkyNBUrahbunQp8+fPZ968eUyaNImrrrqKPXv2cO+992aWee2111i8eDFdunTho48+Yvbs2Xz22Wc89dRTPP744wBMnTqVHj16MHbsWGbOnMnUqVMZMmQI5cqV40LP3FVNmjQBYOTIkSxYsICCXJ/smWee4ciRI3Tq1InPPvuMSZMm0blzZw4fPsyznqlKoqKiGDp0KNOmTaNfv35MmzaNN954g4cffviE7rrnnnuOffv20a5dO8aPH8/s2bOZMmUKzz//PLfffnuBfQ9jshVs5ERuEnA57gHeNKDCqX5OfqaIH8XXsaMbqve3v2VbZPRo34i+MmVUN2wIYf2KmGCj+BISEvTSSy/Vb7755oTyK1as0BtvvFETEhK0ZMmSWqNGDe3evXvm0O5Vq1Zpr169tG7duhobG6tVqlTRK6+8UufPn5/5GWlpaTpw4EBNSEhQETnpaDdAn3rqqaD1/u233wLy27dvr23btg3Imz9/vnbq1EnLli2rZcqU0Y4dO+qCBQtOOM/f//53rV27tsbGxmrr1q31hx9+0Dp16gSM4lP1DZVPSkrSEiVKaLVq1bRz5876/vvvZ5axUXwmv5HNKL5crajrJSJ1gdsB792R94Cxqro2H2LlaYuIFXVz8tVXcNVV7uHdP/4IurhherqbIclze4SePeHTT0NcT2OMCaHTWlFXRG4RkRnACqAhcBdQV1WfiZTgVChceSX06gVBZgTwio6Gf/3Lt//ZZ0HXPTTGmCIvVy0oEckANgD/wQ03D0pVwzrMPOJbUHnQp49v2Hn9+vDLL2D3qI0xRVF2LajcBqh1uD78nKiqnnFq1csfhS5Aqfqe0M1i+3Zo2BC8E26PGAFPPx3CuhljTIicVhefqtZV1Xo5JaB9vte6qNqyBe66yz2dm43ExMDZzl94wd22MsaY4uK05yoQkWoi8i/AFovILRF49134z3/g99+zLXb33W4idHBrHg4Y4BpdxhhTHOR2kEQFEflARHaKyBYRuU+cocAfuId47UGJ3Kpe3bWeVOGvf822WHQ0jBrlm/JoxgwYMyZEdTQhkZGRwfbt2wNS1mVAjCmuctuCehG3zPt4YA/wOvAFrlvvSlU9V1U/zOkDRCRWRMaIyHoROSAiS0TkyhzKPygi20Rkn4iMLXIPAz/+uIs848fDhg3ZFjv3XHjIbxrehx92D/GaomHMmDHUqFGDevXqUa9ePWrVqpXtVEPGFDe5DVDdgH6qOgTogZswdo2qdlTV2bn8jBhgIy6olcctgvix59mqACLSBXgc6ATUBc4AitZyfg0awE03QVoavPJKjkWHD3cj+cBNjH7PPdbVV1QcOXKEmJgYjhw5wpEjR0hNTeXgwYPhrpYxESG3ASoJ9wwUqvoHcBQ4cR3zHKjqIVUdpqrrVDVDVacCa4HWQYr3wU1Ku1xV9wIjgL55OV+h8OST7vWdd8Az63QwZcoEdu19+SV8mGN71RhjCr/cBqgowL9jPB04ralMPRPNngUsD3K4KZDit58CJIpI5awFRWSAiCSLSPLOnTtPp0qh17QpXHcdHDsGX3+dY9F27VzLyWvQIMin5YiMMSYi5TZACTBBRL4QkS+AUsBo775ffu4+TKQE8AEwXlVXBSkSB+zz2/dul8taUFXfVtU2qtrGOzt1ofLii5CSArmYjPPll6FuXbf955/uYd6MjAKtnTHGhE1uA9R4YAuw25Mm4O4n7c6STkpEooD3gePA4GyKHQT8p1r2bh8IUrZwa9gQmjfPVdFy5dw6Ud5RfTNnwuuvF2DdjDEmjHK1YKGq9suPk4mIAGOARKCrqmY3nnY50ALwLmLTAtiuqrkKgoXWzJnQuLFvzY0gLr4YnnjC9xDvk09C587QokWI6miMMSES6kXF3wQaA91VNacV3d4D7hCRJiJSEXgaGBeC+oXPc89Bx47w/PMnLTp0KHjX0Dt+HG65BQ4dKuD6GWNMiIUsQIlIHdws6C2BbSJy0JN6i0htz3ZtAFX9BngFmAms96ShoaprWPTs6WaYePttWJvzBPElSsCECVC6tNtfscINmjDGmKIkZAFKVderqqhqKVWN80sfqOoGz/YGv/KvqWqiqsaraj9VPRaquoZF06bwl79AaqprIp1Ew4aBy3KMH+9mTzLGmKIi1F18JifDh/uaR8uDjb4P1K+fG8nnNXCgb6FDY4wp7CxARZJ69Xwzwj711EmLi8Abb7jGF7gJZW+4wc02YYwxhZ0FqEjz9NNQtix8/rkb1XcSZcvCJ5+4V4DVq11PoT0fZYwp7CxARZpq1dw9qEcfhdbBZoE6UePGMNpv4qkvv4Rnnimg+hljTIjk6jkoE2KPPJLnt9x8MyxZAn/7m9t/8UX3/O+NN+Zz3YwxJkSsBRXpDh+GXM5u/dJLcMUVvv1+/eCnnwqoXsYYU8AsQEWy6dPdePIRI3JVPDrazXJ+1llu/8gR6NYN1q0ruCoaY0xBsQAVySpUgE2b4O9/h99+y/VbvvgCypd3+9u2wZVXwp49BVVJY4wpGBagItm557p+uuPH87RKYcOGbhBgyZJuf9UquPpqNwzdGGMKCwtQke6VV6BSJZgxI0+rFLZvD++959ufM8cNP09PL4A6GmNMAbAAFemqVPENzXvwQdi7N9dvvfFGGDnSt//ZZ27OPlsu3hhTGFiAKgz69oVLLoEdO9xaG3nw4INw//2+/VGjXJ4FKWNMpLMAVRhERcGbb0KDBtC9e57eKgKvvQa9e/vy/vEPePxxC1LGmMhmD+oWFk2bwsqVbix5HkVFwbhxcOwYfPqpy3vlFbdcx7Bh+VpLY4zJN9aCKkz8g9OGDdmXCyImBv7zH+jRw5c3fLgLUNaSMsZEIgtQhdFjj8GZZ8LcuXl6W4kS8PHHgbNNDB8ODz9sQcoYE3ksQBVG0dGQluYGTxw+nKe3xsbCpEnQpYsv7/XX4c47bQi6MSayWIAqjIYOdfekfvstV+tGZVW6tHuQt2dPX96YMXDLLe6ZYGOMiQQWoAqj2Fi3xnt0tJsG6ZtvTukjPvoocEXejz920yL9+We+1dQYY06ZBajCqnVreP55t92nj5t0L49iYmDsWLj3Xl/ed9/BRRfB2rX5VE9jjDlFFqAKs0cfhY4d3QO8Q4ac0kdERbnnoryxDtxo9vPPh/nz86mexhhzCixAFWZRUfD+++4p3NdfP+WPEXG3sv7zH98Eszt3wqWXujxjjAkHC1CFXVISTJgACQmn/VE33+zmpK1c2e0fPepi33332eAJY0zoWYAqStLS3JO3W7ee8kdcfLHr2mvUyJf3f//nWlNbtpx+FY0xJrdCGqBEZLCIJIvIMREZl0O5viKSLiIH/VKHkFW0sHrySffk7Q03nFaTp359WLAgcBj63LnQqpVrYRljTCiEugW1BXgeGJuLsvNUNc4vzSrYqhUBDz8MNWrAjz+e8qAJr/h4+OQTN2dflOenZPt26NwZHnnEzetnjDEFKaQBSlUnqeoUYHcoz1tsJCa62WBLlHD9cuPGndbHibhgNH164C2uV1+FCy5wo/2MMaagRPI9qHNEZJeIrBaRZ0Qk6MzrIjLA022YvHPnzlDXMfJccAH8619ue8AAmDXrtD+yY0f4+Wf3EK/X0qWuy++112yKJGNMwYjUAPU90AyoCvQEbgYeCVZQVd9W1Taq2iYhH0ayFQkDBsADD0BqKlx3nZsS6TQlJsJXX7mGWWysyzt61PUqXnihC2DGGJOfIjJAqeofqrpWVTNU9WfgOeD6cNerUHn1Vbe2xvnnu+iSD0Rg8GBIToYWLXz5ixa51tQzz7igZYwx+SEiA1QQCki4K1GoREfDhx/Cl1+6EQ/5qFkzF5Sef973YG9amttv0gSmTLHlO4wxpy/Uw8xjRKQUEA1Ei0ipYPeWRORKEUn0bDcCngE+D2Vdi4QyZdyEe+CG3f31r/n2xG2JEm72iaVL3dx9XmvXwrXXuuU8bBCFMUVDWhps3Oiekfz0Uzc92iOPuBUQXnih4M4b6iXfnwaG+u3/BRguImOBFUATVd0AdALGiUgcsB2YALwY4roWLbff7uYtWroUPvjglJaOD6ZxY/jhBxg1Cp5+GvbscfnTp8PZZ8Mdd7iuv5o18+V0xph8dvgwbN4MmzZl/7p9O2RkBH9/hw6ntOpProQ0QKnqMGBYNofj/MoNAU7vQR4T6OGHXXffxIlQsSL8+9/uplI+iIqCe+6BXr3g2WfhrbfcD3N6Orz9tlsZZPBgePxxqFIlX05ZaB07doxly5Zl7q9fv/6EMjt37mTRokWZ+w0bNiQ+n7tpTfFw5IgLMBs2uBbQhg0u+QegvXtP7xybN+dPXYMRLUI3C9q0aaPJycnhrkbkmj3b9b0dO+Yixj//mW9Byt+yZW4Q4cyZgfnlyrn8++4rvoFqypQpXHfddQEB58CBA2T4/XkaHx+PeP5dDh06xAsvvMCjjz4a8rqayJaR4VbZyRp8/Pfz88mbxEQ3D0DNmoGvdetC+/an99kislhV25yQbwGqmPn6a7jmGncv6p573DNTUfl/K1IVvv3Wzb6U9Z+kdGnX9ffww+6HuzhJTU2lRo0a5PaZvdKlS7NhwwaqFNeIXozt23di8MnaCkpNPf3zlCjhAo03ZQ1ANWtC9eq+AVEFwQKU8fnmGxekjh1zXX333FNgp1J1o/qefhpWrAg8Fh0NN94IDz4IbU740Sy6Ro8ezYMPPsihQ4dyLBcbG8ugQYMYOXJkiGpmQuX4cdfFll3w2bgR9u8//fNER7sAU7s21Krle61Vyxd8qlQpkL9R88QClAk0bZq7QfSf//ievC1A6eluSfmXX4aUlBOPt2kDAwe6gFWmTIFXJ6xy24qy1lPhpOrWEM0p+Gzblj+PYlSpEhh8sm5Xq5Zv46EKlAUok7NDh9z9qAKODqrwv/+5QJX1HhVAhQpuBfs+faBlywK5RRYRTtaKstZT5Dp4MOfgs3Fj/kymXLp09oHH2woqKn/MWYAy2Tt+HLp3d0Hqyy/dKL8QWLTITZ308cfB/0M3aQK33uqetahdOyRVCpmTtaKs9RQeaWlu3bPsgs+GDac/6g1cl1r16tkHn9q13cKhRfUPtKwsQJnsrV8Pl1zi/gc2buyC1Jlnhuz0u3a5idffegvWrAlepm1b9wDw1Ve79aqKguxaUbGxsQwcOJDXXnstTDUrmlTdz5p/S8c/8Gzc6IJTds/75EWFCjkHn6QkNzjBOBagTM42boSuXeGXX6BSJfjsM/cEXghlZLgFEd97DyZNcg8QBtOsmQtUV1/t5gAsDH3swWTXirLW06k5cCD7wONN+TFXZMmSvi42b+DJOgihXLnTP09xYgHKnNz+/a4/7auv3BRJb7zhZkYPg4MH3ei/CRPcrBTZ/VVbqZJbDqRzZ5fOOKNwdYtkbUXZvafgjh93w6qDBR7v9p9/5s+5qlXL+d5P1arhH/VW1FiAMrmTnu6mfHj1Vbc/dSp06xbWKu3c6aoxZYobYJHTX8F16sDFF7slQC68EJo3901HGImytqKKW+tJ1QWWzZuDpy1b3OuOHfkz6q18+cDWT9btmjVDMqjVZGEByuTNu++6Nd+//DKi+tAOHXJByhustm3LuXyZMnDuuW4Ye4sWLjVqVLAPHeaVtxWVlpZWpFpPhw+7Ody2bs05AB05kj/ni431BZzsApDNGBWZLECZvFP19Zdt3QoLF7obPxFC1T38++23Ls2a5boGT6ZECTdCsHlz99qggUv164dn2K63FXXgwAE2btwY0a2nY8dc0Nm27eSvBw7k33n9R71lF4ASEgpX967xsQBlTl16urvBM2sWDBoEr7wSkQ9gpKbCTz/BvHm+tHFj3j6jRg0XrOrVC5zqxZsqVSqYX4KTJ09m3bp1PPjgg/n/4dk4ehR2784+7doVuL9zZ/7d5/FXtmzgVDvBUrVqkd1Va06PBShz6lR9C8Ckpbnf4OPGBS4EFaE2b3Zr2KSk+FKQCcRzLTbW/aVeubJ7it//tWJFiItzv3CzvpYt61puMTEu+W/HxLheVFX3t4B3Jnj/14wMN1DgyBEXWI4c8SX//cOHXctl3z435mX//uy386trLTsxMW6C0erVfYEmKenE4BMfby2f4s4ClDl9P/0Et90Gy5e7PpchQ2D4cChVKtw1y5N9+9yM68uWwerV8NtvLq1d6wKCyV50tAs6iYmuVZN12/+1YkULPCZ3LECZ/HHsGAwb5rr5MjLcjZzFi4tE/0tqKqxb54LVpk0npo0bc3ePq7CIjnYtP/9WoH/KmpeQ4Lo4bYi1yW/ZBajC/1vFhFZsLLz0khss0bevmxW9CAQncN1u3gET2Tl4MPD+jP/rvn1ulOHBgy75bx8+7HpHU1PdqzelpgYumRAd7QJAsNeYGDc/mzeVKhV8Oz7epfLlfdvB8sqWtRaOiXCqWmRS69at9XQB6i6Lz1VXXaWAfvHFF5l5o0aNUkDvvPPOzLzNmzcroNWrVw94f6tWrRTQ5OTkzLyhQ4cqoEOHDs3MS05OVkBbtWoV8P7q1asroJs3b87Mu/POOxXQUaNGZeZ98cUXCuhVV10Vku9UEnTx3LmZeROvv17vA33u6acL7XcK179TRkbR+06q9p2Kw3fKD0CyBvmdXjT+9DVhcRxQ7wNFBw/S9euv6QXseeMN98BRz57hrF6hYi0ZY05k96BM/lB10z08+iisWuXyLrzQratxySXhrZsxJqJldw/Kbnea/CHiluz4+Wd48003Ydm8edCuHVx6qXt60xhj8sAClMlfMTFw993w++8wdKi7K79tmxsSZowxeWAByhSMcuXccPT162HiRN98fhs2uMnxxo/Pn2VHjTFFVkgDlIgMFpFkETkmIuNOUvZBEdkmIvtEZKyI2BzDhVH58u5ZKa/RoyE52Q1Rr13bPehr3X/GmCBC3YLaAjwPjM2pkIh0AR4HOgF1gTOA4QVdORMCTz3lZkpv3tytoTBsmJvkrmdPNz25McZ4hDRAqeokVZ0C7D5J0T7AGFVdrqp7gRFA3wKungmFUqVc62npUpg50z3wm5HhltAdN85XrgiNLjXGnJpIvQfVFEjx208BEkWkctaCIjLA022YnHXpbBPBRNyS8lOmuDmEXnwRBg/2Hf/0U7ee+8svu0nyjDHFTqQGqDhgn9++d7tc1oKq+raqtlHVNgkJCSGpnMlnSUnwxBOBs6NPmQJLlrjVfc84A84/H0aOdLO7GmOKhUgNUAcB/7Uvvdv5uASaiWhjxsDkyXDTTW7tqYUL3ezpDRvCjTeGu3bGmBCI1AC1HGjht98C2K6qJ7t3ZYqKUqXcRLQffuhWyvv4Y+jd202n3cLvR+Onn9wDwq+/7hZ7ysgIW5WNMfkrpHPxiUiM55zRQLSIlALSVDUtS9H3gHEi8gGwFXgaGBfKupoIUqYM3HCDS2lpgc9P/e9/boqlqVPdfuXKbuaKSy+Ftm3daEGb6M6YQimkc/GJyDBgaJbs4bhh5yuAJqq6wVP2IeAxoDTwGXC3qub4ZKfNxVcMbd0K06fDd9/BjBlu4SavatVgyxZfgJoxA84+203DZIyJGLZgoSn6VGHNGhesZs92S7r+61/u2P79UKGCK1OnDpxzDrRs6boLW7Z0edbSMiYsLECZ4u2PP+COO2DRIreSYFZTp0K3bm77p59cQGvc2LW2LHAZU6BsRV1TvJ1xhnswOC3NDVVfutSllBQ3nN1/4MVrr8EHH7jtChWgUSNfOu88d3/LGFPgLECZ4iUmBpo0cemWW1xe1l6Ehg3hggtg5Ur480+YP98lcDNfeAPUzp2u1XXGGVCvnktnnAF160KNGm79dWPMKbMAZUzWLrxnnnFJ1c0XuGqVLzVp4iu3Zo3rMly0KPjn/vij7+HjTz+FFSvcvIM1arjXpCTXQrMuRGOCsgBlTHZEIDHRpfbtTzx+9tkwZ467v7V2rXv94w83ddPmzVC9uq/sp5+6ZUeyKlECrrwSPv/c7aemwtNPu3tf3nMnJrr9SpWgZMmC+a7GRCALUMacqrJl3bNWbdueeCwjI7BldNNNcOaZbhi8N23dCgcOBJbbuRNeeSX7c06Z4roZwT3EPGWKC1yVKwe+Vq3qpocyphCzAGVMQYjKMknLNde4lNWRI3D0qG+/VCk3ce727S7t2OF73bPHdQl6LV7sZtgIpk4dWLfOt1+9umudxce7Nbq8KT7ezdBxxRWu3Lp1MG+e71i5chAX50tlyliXpAkZC1DGhFPp0oGDKSpVchPnBqMaOKCjb19o08YFrt27A1+rVAl8365dbgTj7iCzhZ17ri9Aff899OmTfX0PHnQtR4Cbb3b31cqW9QUw7/bFF7vAB26gydSpLrh5v69/qlXLBWZjsrAAZUxhIRLYemnWzKXcvO/gQfds1759Lvlvn3uur2ytWtCrl+/YoUPuvQcPwuHDgcH0119h2bLg50xL8wWotWvh1luzr9/8+b7uyEGDYOzY4IGsWTN3zGvAAIiN9R2PjfWljh19A1rWr4flywOP+yf/h7QzMk5s/ZqwsQBlTHEQGwsJCS7lxDuPYW5MnuxaR94AdvCgL6A1bOgrV66cG9J/+LDr0vQm736838IFhw+7Ls+jR2Hv3sDz+QfntDQYPTr7uo0e7QtQX33lAl92/CcYbt3aBd1ggax3bxjqmalt1Sq4/343yCVYevZZF+zB3SdcujR4uerVoUcPV07V1TW7z6xVy82O4r1Ohw+7/Oho9/hETIzbLkJdsBagjDGnpk4dl06mfn3fg88nM2YMvPFG8EAWGxtY9u23A8sdO+ZLTZv6ytWsCV26BB73Jgj8hZ6a6gKW9zP97drl2969201UnJ377gsMUOPHBy93/vm+AJWa6mbmz86YMXD77W577Fi4997g5WJjA+9rtmvnWrveIOYNZDEx8Je/wJNPunK//AL33BNYzj+NHAm1a7uy777rWr733pu7VvwpsgBljIkcUVHuXlWZMjmXi4mBO+/M3Wf26OELAifzyy++GfOzJv+WXpMm8PXXLqhkTcePu6Dodc01LpAHK1u3rq+cKnTtmv1nVvZbULxkSXe/Mi3Nl9LTXcragtq1yw2yCcY//88/3WMT2Rk2zLf93XcwYQJcd12BBiibi88YY4oKVRekYvzaHnv2uACXnh4Y0NLSXJdhUpIrt2+f697MWsb7vssv9wXpmTNdq6xbN19L8TTYZLHGGGMiUnYByoarGGOMiUgWoIwxxkQkC1DGGGMikgUoY4wxEckClDHGmIhkAcoYY0xEsgBljDEmIlmAMsYYE5GK1IO6IrITWH+aH1MF2HXSUkWfXQcfuxY+di0cuw4++XEt6qjqCTMZF6kAlR9EJDnYE83FjV0HH7sWPnYtHLsOPgV5LayLzxhjTESyAGWMMSYiWYA60dvhrkCEsOvgY9fCx66FY9fBp8Cuhd2DMsYYE5GsBWWMMSYiWYAyxhgTkSxAGWOMiUgWoDxEpJKITBaRQyKyXkRuCXedCoKIDBaRZBE5JiLjshzrJCKrROSwiMwUkTp+x0REXhaR3Z70iohIyL9APhKRWBEZ4/n3PiAiS0TkSr/jxeZ6iMgEEdkqIvtFZLWI9Pc7Vmyug5eINBCRoyIywS+vWF0HEZnluQYHPelXv2OhuRaqaskNFPkQmAjEARcD+4Cm4a5XAXzP64BrgDeBcX75VTzf+QagFPA3YL7f8buAX4GaQA1gBXB3uL/PaV6LssAwoC7uj7WrgAOe/WJ1PYCmQKxnuxGwDWhd3K6D3/f6H/ADMMGzX+yuAzAL6B8kP2TXIuwXIRKS5xfVceAsv7z3gb+Gu24F+J2fzxKgBgBzs1yTI0Ajz/5cYIDf8Tv8fyiLSgKWAT2L8/UAGgJbgV7F8ToANwEf4/548Qao4ngdsgtQIbsW1sXnnAWkq+pqv7wU3F+VxUVT3HcGQFUPAWvwXYOA4xTB6yMiibifheUUw+shIv8WkcPAKlyA+i/F7DqISDzwHPBwlkPF6jr4eUlEdonIjyLSwZMXsmthAcqJwzVZ/e0DyoWhLuFysmuQ9fg+IK6w97N7iUgJ4ANgvKquohheD1UdiPt+lwCTgGMUv+swAhijqhuz5Be36wDwGHAGrpvubeBLETmTEF4LC1DOQSA+S1487n5EcXGya5D1eDxwUD1t+MJMRKJwXbrHgcGe7GJ5PVQ1XVXn4O4f3EMxug4i0hLoDLwe5HCxuQ5eqrpAVQ+o6jFVHQ/8CHQlhNfCApSzGogRkQZ+eS1wXT3FxXLcdwZARMoCZ+K7BgHHKSLXx/NX3RggEeipqqmeQ8XyeviJwfd9i8t16IAbILNBRLYBQ4CeIvITxes6ZEcBIZTXItw34iIlAR/hRvKVBdpSdEfxxeBG3ryEazWU8uQleL5zT0/eywSOzLkbWIlr7id5fuAK9Sglz/d6C5gPxGXJLzbXA6iKGxgQB0QDXYBDwNXF7DqUAar5pVeBTz3XoNhcB8/3qeD5OfD+fujt+ZloGMprEfYLESkJqARM8fwjbABuCXedCuh7DsP9JeSfhnmOdcbdID+CG8FT1+99ArwC7PGkV/DM5VhYE1DH8/2P4rolvKl3cboenl84s4E/gf3Az8CdfseLxXUIcl2G4RnFV9yug+dnYhGu2+5P3B9xl4X6WthkscYYYyKS3YMyxhgTkSxAGWOMiUgWoIwxxkQkC1DGGGMikgUoY4wxEckClDHGmIhkAcqYIkpEVESuD3c9jDlVFqCMKQAiMs4TILKm+eGumzGFRUy4K2BMEfYtcGuWvOPhqIgxhZG1oIwpOMdUdVuWtAcyu98Gi8hXnmWz14vIX/zfLCJni8i3InJERPZ4WmXls5TpIyI/i8gxEdkuIuOy1KGSiHwiIodE5I+s5zAmklmAMiZ8hgNfAC1x6+28JyJtAESkDPANbm7A84BrgYuAsd43i8hdwCjgXaA5bimErLNGPwt8jptReiIwVkTqFNg3MiYf2Vx8xhQAT0vmL7iJaP29oaqPiYgC76jqnX7v+RbYpqp/EZE7cbNp11TVA57jHYCZQANV/V1ENuEmM308mzoo8FdVfcKzH4ObDHaAqk7Iv29rTMGwe1DGFJzvgQFZ8v70256X5dg8oJtnuzGwzBucPOYCGUATEdmPW85gxknqsMy7oappIrITt7yGMRHPApQxBeewqv5+iu8V3FIgwXgXjsuN1Cz7inXtm0LCflCNCZ8Lguyv9GyvAFqISDm/4xfh/s+uVNXtwGagU4HX0pgwsRaUMQUnVkSqZclLV9Wdnu3rRGQRbsG363HB5nzPsQ9wgyjeE5FngYq4ARGT/FplLwCvi8h24CvcirCdVHVkQX0hY0LJApQxBaczsDVL3magpmd7GG7Z7H8CO4F+qroIQFUPi0gX4O/AQtxgi8+B+70fpKpvishx4GHcstt7gP8W0HcxJuRsFJ8xYeAZYXeDqn4a7roYE6nsHpQxxpiIZAHKGGNMRLIuPmOMMRHJWlDGGGMikgUoY4wxEckClDHGmIhkAcoYY0xEsgBljDEmIv0/+yhYT8ErZVIAAAAASUVORK5CYII=)]

np.random.seed(42)
m = 100
x = 6 * np.random.rand(m, 1) - 3
y = 2 + x + 0.5 * x**2 + np.random.randn(m, 1)

x_train, x_val, y_train, y_val = train_test_split(x[:50], y[:50].ravel(), test_size=0.5, random_state=10)
poly_scaler = Pipeline([('poly_features',PolynomialFeatures(degree=90,include_bias=False)),('std_scaler',StandardScaler())])
x_train_poly_scaled = poly_scaler.fit_transform(x_train)
x_val_poly_scaled = poly_scaler.transform(x_val)
sgd_reg = SGDRegressor(max_iter=1,tol=-np.infty,warm_start=True,penalty=None,learning_rate='constant',eta0=0.0005)
minimum_val_error = float('inf')
best_epoch = None
best_model = None
for epoch in range(1000):
    sgd_reg.fit(x_train_poly_scaled,y_train)
    y_val_predict = sgd_reg.predict(x_val_poly_scaled)
    val_error = mean_squared_error(y_val, y_val_predict)
    if val_error < minimum_val_error:
        minimum_val_error = val_error
        best_epoch = epoch
        best_model = deepcopy(sgd_reg)

#画图
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
                       penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)

n_epochs = 500
train_errors, val_errors = [], []
for epoch in range(n_epochs):
    sgd_reg.fit(x_train_poly_scaled, y_train)
    y_train_predict = sgd_reg.predict(x_train_poly_scaled)
    y_val_predict = sgd_reg.predict(x_val_poly_scaled)
    train_errors.append(mean_squared_error(y_train, y_train_predict))
    val_errors.append(mean_squared_error(y_val, y_val_predict))

best_epoch = np.argmin(val_errors)
best_val_rmse = np.sqrt(val_errors[best_epoch])

plt.annotate('Best model',
             xy=(best_epoch, best_val_rmse),
             xytext=(best_epoch, best_val_rmse + 1),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.05),
             fontsize=16,
            )

best_val_rmse -= 0.03  # just to make the graph look better
plt.plot([0, n_epochs], [best_val_rmse, best_val_rmse], "k:", linewidth=2)
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="Validation set")
plt.plot(np.sqrt(train_errors), "r--", linewidth=2, label="Training set")
plt.legend(loc="upper right", fontsize=14)
plt.xlabel("Epoch", fontsize=14)
plt.ylabel("RMSE", fontsize=14)

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

问题1、2与4的答案
提前终止的目的是为了防止过拟合，如果我们只要返回使验证误差最低的参数，就可以获得验证集误差更低的模型。

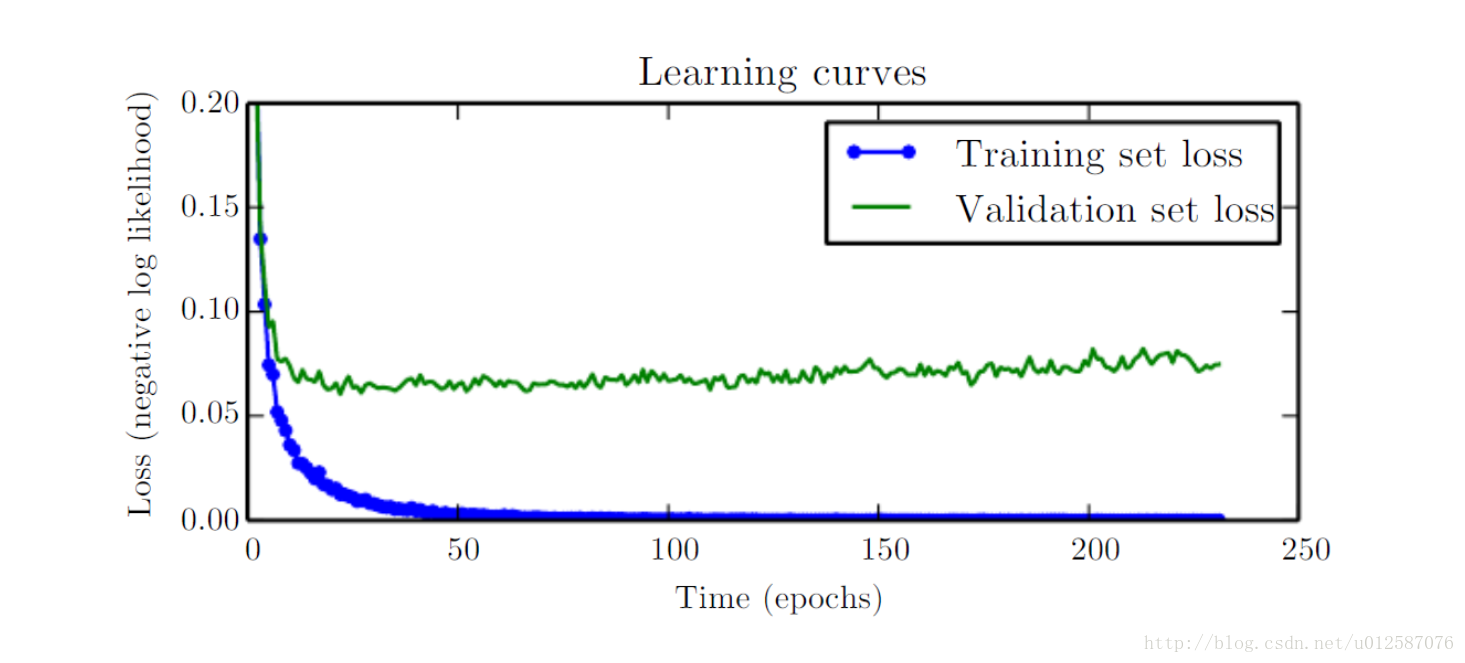
图1.学习曲线(横轴为训练轮次，纵轴为负的对数似然)
对图1的注释：
蓝色曲线表示训练集上的loss随着训练轮次的变化而变化的情况。
红色曲线表示测试集上的loss随着训练轮次的变化而变化的情况。
注释:红色曲线是每训练完一个epoch后就测试一次所得到的曲线。
从图中可以看出，测试误差在前几个epoch中逐渐减小，但是训练到某个epoch后，测试误差又有了小幅度的增大。这说明此时发生了过拟合。

发生过拟合是我们所不愿意看见的，我们可以利用提前终止(early stopping)
来防止过拟合的发生。

提前终止是指：在测试误差开始上升之前，就停止训练,即使此时训练尚未收敛(即训练误差未达到最小值)。

首先我们要保存好现在的模型(网络结构和权值),训练num_batch次(即一个epoch),得到新的模型。将测试集作为新模型的输入,进行测试。如果我们发现测试误差比上次得到的测试误差大，我们并不会马上终止测试，而是再继续进行几个epoch的训练与测试，如果测试误差依旧没有减小，那么我们就认为该试验在上一次达到最低测试误差时停下来。具体算法可参见《deep learning》

问题3的答案
该问题是为了回答为什么提前停止可以起到正则化的作用。
首先，我们对损失函数在ω∗ω∗的邻域内用Taylor展开式展开(只展开至二次)，则有

J′(ω)=J(ω∗)+1/2(ω−ω∗)TH(ω−ω∗)J′(ω)=J(ω∗)+1/2(ω−ω∗)TH(ω−ω∗)

其中H是Hessian矩阵。这里之所以没有一阶导数的信息，是因为 ω∗ω∗是最优解，在 ω∗ω∗的邻域中，可以近似地认为梯度为0。
对 J′(ω)J′(ω)求梯度，得到

∇ωJ′(ω)=H(ω−ω∗)∇ωJ′(ω)=H(ω−ω∗)

我们将参数向量 ω(0)ω(0)初始化为原点0。由梯度下降法，可以得到如下公式：

ω(τ)=ω(τ–1)−α∇ωĴ (ω(τ−1))ω(τ)=ω(τ–1)−α∇ωĴ(ω(τ−1))

ω(τ)=ω(τ−1)−αH(ω(τ−1)−ω∗)ω(τ)=ω(τ−1)−αH(ω(τ−1)−ω∗)

ω(τ)−ω∗=(I−αH)(ω(τ−1)−ω∗)ω(τ)−ω∗=(I−αH)(ω(τ−1)−ω∗)

将H进行特征值分解： H=QTπQH=QTπQ，其中Q是标准正交矩阵，π是对角矩阵。
那么

ω(τ)−ω∗=QT(I−απ)Q(ω(τ−1)−ω∗)ω(τ)−ω∗=QT(I−απ)Q(ω(τ−1)−ω∗)

Q(ω((τ))−ω∗)=(I−απ)Q(ω((τ−1))−ω∗)Q(ω((τ))−ω∗)=(I−απ)Q(ω((τ−1))−ω∗)

其中 αα足够小以保证|1−απi|<1|1−απi|<1。

Qω(τ)=(I−(I−απ)τ)Qω∗Qω(τ)=(I−(I−απ)τ)Qω∗

在分析L2正则项的时候，Qω̃ =(I−(π+εI)−1ε)Qω∗Qω̃=(I−(π+εI)−1ε)Qω∗
由上面两个式子比较可知，如果下式成立：

(π+εI)−1ε=(I−απ)τ(π+εI)−1ε=(I−απ)τ

则L2正则化和提前终止可以认为是等价的。进一步，有

ε/(πi+ε)=(1−απi)τε/(πi+ε)=(1−απi)τ

两侧取对数，可知：

log(ε/(πi+ε))=τlog(1−απi)log⁡(ε/(πi+ε))=τlog(1−απi)

作一个简单的近似：

−log(1+πi/ε)=τlog(1−απi)−log⁡(1+πi/ε)=τlog⁡(1−απi)

−πi/ε=−ατπi−πi/ε=−ατπi

(比较Taylor展开式的第一个非常数项，Taylor展开式是唯一的)
从而

τ=1/αετ=1/αε

以上的推导说明了提前终止可以起到正则化的作用。

逻辑回归

估计概率

逻辑回归模型的估计概率
$$\begin{gathered} \hat{p}=h_{\Theta }(x)=\sigma (x^T\Theta ) \\ 逻辑记为\sigma (.),是一个sigmoid函数（即S型函数），输出一个介于0和1之间的数字 \end{gathered}$$
逻辑函数
$$\sigma (t)=\frac{1}{1+exp(-t)}$$
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AhRbsEOJ-1658889211623)(data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAoAAAADQCAYAAACX3ND9AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAwSUlEQVR4nO3daXgUVfr38e9NwqJsgigqEhFlFEUFxXHHUlGWv4M4OMq4sKiDKKigKCIKKiMyDuMDOq64oKIOLuiIyiIqIDoqIFFBaVSEALKFJSQhG8l5XlTS6YQsHeikk/Tvc111dZ+q09V3V046d05VnWPOOUREREQkdtSJdgAiIiIiUrWUAIqIiIjEGCWAIiIiIjFGCaCIiIhIjFECKCIiIhJj4qMdQDhatGjh2rRpE+0wRCRGBQIBAI477rgoRyIisWrp0qXJzrlDIrW/GpEAtmnThiVLlkQ7DBGJUZ7nATB//vyoxiEiscvM1kZyfzoFLCIiIhJjlACKiIiIxBglgCIiIiIxRgmgiIiISIxRAigiIiISY5QAioiIiMQYJYAiIiIiMUYJoIiIiEiMCWsgaDMbCgwATgLecM4NKKPucGAkcADwDnCzcy4rf1tz4AXgEiAZGOWce30/4t9LVlYW27dvJzU1ldzc3EjuWqTKxMXF0bhxY5o3b079+vWjHY6IiNQy4c4E8jvwd6AbfmJXIjPrBtwDXJj/mneBB/PXATwJZAMtgY7Ah2b2nXNuxb4EX1xWVhZJSUk0a9aMNm3aULduXcwsErsWqTLOOXJycti1axdJSUkkJCQoCRQRkYgK6xSwc26Gc+49YFs5VfsDLzjnVjjndgDj8HsOMbOGQB/gfudcmnNuEfA+cF157x8IBJg6dSoAOTk5eJ7HtGnTANi9ezee5zF9+nS2b99OkyZN2LZtG+np6ZgZOTk5BAIBdu7cGXx9IBAgJSUFgOzsbAKBALt27QL8JDIQCJCamgpAZmYmgUCAtLQ0ADIyMggEAqSnpwffPxAIsHv3bgDS09MJBAJkZGQAkJaWRiAQIDMzE4DU1FQCgQBZWVkA7Nq1i0AgQHZ2NgApKSkEAgFycnIA2LlzZ5Hyjh07CAQC7NmzB4Dt27cTCASCvZ3btm0jEAiQl5cHQHJycnAeU4CtW7cWKW/ZsoVVq1YFy5s3b+bnn38Oljdt2sQvv/wSLG/cuJFff/01WP79999ZvXp1sLxhwwZ+++23YHn9+vWsWbMmWF63bh1r1xbOZpOUlERSUlKwvHbtWtatWxcsr1mzhvXr1wfLv/32Gxs2bAiWV69eze+//x4s//rrr2zcuDFY/uWXX9i0aVOw/PPPP7N58+ZgedWqVWzZsiVYDgQCbN26tUg5OTkZgLy8PAKBANu2+b8Gubm5BAIBtm/fDsCePXsIBALs2LEDYJ/bXlpaGvXq1aNRo0ZkZmby/fffA7B8+XI8z2Px4sUAJCYm4nkeiYmJACxevBjP81i+fDkAX375JZ7nBX/eCxYswPO84M9r3rx5eJ4XPN6zZ8/G87zg8Zo5cyae5wU//4wZM/A8Lxj/9OnT8Twv2PanTZuG53nBtjp16tTgFGoAU6ZMoWvXrsHyU089RY8ePYLlyZMn06tXr2B54sSJ9OnTJ1ieMGECffv2DZbHjRvHtddeGyyPGTOGgQMHBsujRo1i0KBBwfKIESMYMmRIsDxs2DCGDRsWLA8ZMoQRI0YEy4MGDWLUqFHB8sqVKxkzZkywfO211zJu3LhguW/fvkyYMCFY7tOnDxMnTgyWe/XqxeTJk4PlHj168NRTTwXLXbt2ZcqUKcGy53lhfe+B/73heR4zZswA/N97z/OYOXMm4P8ee57H7NmzAf/30PM85s2bB/i/R57nsWDBAsBv957n8eWXXwJqe9Fqe7m5kJkJ1157M3fdNZ6tW2HjRrj88tu4444n+Pln+Okn6N79Lm677UWWLoVvvgHPu5dbbnmDBQvg00/hrLPGMHjwe3z0EcycCaee+iCDBs3inXfgrbegQ4e/c+ONn/Laa/Dqq3D88Y9w442LePFFePbZPRx33D+5/vqveeYZmDQpm3btJjNw4Lc8/jhMmJDBscf+mwEDvudf/4IHH0znmGOeZsCAH3n0UbjvvlTatn2OgQNXMX483H33To4++nkGDvyVceNg+PDttGnzIgMHruGBB2Do0GTatJnKwIHrGDMGbrppC0cd9QrXX/87990HN964iaOOepUbbtjMvffCgAEbSUh4jRtv3Mo998B1160nIeF1/va3bYwcCVdfnURCwuvcdNNORo6Eq65aQ+vWbzB48C7uuguuuOI3Wrf+DzffnM6IEXD55b/SuvV0hgzZzYgR0KvXz7RuPZ2hQ7O480649NIArVtP59Zbc7jjDujR4yeOPPJNhg3L5Y47oFu3FRx55JvccQfccQdcfPEPJCS8w/DhMHw4XHjhd7Rp826w7HnLaNv2v8Fyly5LOPbYDxg2DIYNg3POWcwf/vARIc0lYiI9F/CJwH9Dyt8BLc3sYCAByHXOrSq2/fySdmRmg4BBQNi9H6mpqbRu3Tr4B1ekpouPjyc+vkZM2S1Sa+XlGdnZB7BuHaSmwvr1R7BpUx0++ADS0yExsRNbtvyBf/wDMjLgs8+6k5a2h0GD/PI331xHdrZxySWQlQWrVg1jz566zJ0L2dmwefM48vLiefFFv5yR8SR5eXEU/j/xNACF/088DsD/+38F5X8yZw488URBeTwLFsDTTxeUH+Krr+DZZwvKY1m2DAr/37iPFSvghRcKyqMIBArK8cBdrFoFL70EUA+4nV9+Af//kwOAoRT2CzQEbqawX6AxMIjCfoGDgBvzXwvQHLg+pNwCGBBSPhTol//eAIcB1/HiiwXlw4FrQmI/Eria558vKCcAV/PccwXlNkCbkGNxNHA0zzxTUD4GOIbC/83aAe148smC8nHAcfz73wXl9kB7Cv+3OxE4MeRncxJwEpMmFZRPAU4JKXcCOoWUOwOE7O/0YuXIMedc+JXN/g4cWdo1gGb2KzDEOTc7v1wX/5Tv0UBr4C3n3GEh9f8GXOOc88p6386dO7slS5aUG99PP/3E8ccfr9O+Ums451i5ciXt27ePdigxraA3af78+VGNQ/adc7BzJyQn+8u2bUWf79zpLzt2FD7fudNP+PI7GqucGdSt6y/x8YWPoUtcXOFjwRJarlOn6LaCcp06pS9mRR9Lel6wFC+HLgWfIZxtoeWC52WtK+mxrOfFj+u+1g9n/f7WLa3+8OG21DnXuWJ7Kl2kuxbSgCYh5YLnqSVsK9ieGskAlPxJbaL2LFK+Xbtg3bqiy8aNsHkzbNrkL5s3+71r+8IMGjWCxo2hSRP/ecOGhcuBBxY+HnDA3kuDBlC/fuFj6FKvXtGlbt3Cx7i4yB4nqdmGD4/s/iKdAK7A7998M798CrDZObfNzDKBeDNr55z7OWR7RG4AERGR2mnPHlizBn79tXBZvdp/XLvWTwDD0bgxHHIItGgBBx9c+HjwwdC8ORx0kL80a+Y/Nm3qJ3wHHuj3dInUJuEOAxOfXzcOiDOzBsAe59yeYlVfAaaa2WvARuA+YCqAcy7dzGYAD5nZjfh3AV8GnB2BzyEiIjXcnj2wahWsWAE//li4BAKQf39HiQ44AFq3LlyOPBJatYLDDoOWLQsfDzyw6j6LSHUXbg/gfcDYkPK1wINm9iLwI3CCcy7JOTfbzB4FPqNwHMDQ190CvAhswb+j+OZIDQEjIiI1R3a2n+gtXQrffus/fv+9f9drSVq3hmOPhbZt4ZhjCpc2bfzeO10tIVIxYSWAzrkHgAdK2dyoWN3HgMdK2c92oHfY0YmISK2wcyd88QV8/jksWgSLF5d8TV6bNtChA5x4Ipxwgr8cf7x/3Z2IRI7GlxARkYhLS/PHoJs7FxYuhOXL/TtxQ7VrB6edBqee6j926uRffycilU8JoEiIhQsXMnHiRJYuXcrvv//OSy+9xIABA6Idlki155x/SnfWLJg92+/pC71ur149OP10OPdcOO88OPtsJXsi0aQEUCREWloaHTp0oF+/fvTr1y/a4YhUa87B11/Dm2/C22/7w68UqFMHzjwTuneHCy7wk78DSp1IVESqmhJAkRA9e/akZ8+eAOr5EymBc/71e2++6U8jFjKTIy1b+glf9+5w8cX+8CoiUj1pZCMpol+/fhx66KHBuY7DsXTpUsyMFwrn4hGRWmbjRhg/3r8T94wz4F//8pO/I4/0B6j93//g99/96cH69lXyJ1LdKQGUoCVLljBt2jTuueceGjZsuNf2xx57DDPj9ddfL7L+tNNOo3fv3tx3332kpaVVVbgiUslyc/1r+v78Z38YltGj/QGYjzgCbr/dv6t37Vp47DH/dK8GSxapOfTrKkH33nsvTZo04eabby5x+7fffgv4CV9xo0aNYtOmTTz++OOVGqOIVL4dO/zevrZtoWdPePddf/3ll/sJYVISTJrk38ihpE+kZtKvrgCwatUq5s2bx5VXXskBpVypvXTpUho1akS7du322vbHP/6R448/nmeffZbc3NzKDldEKsH69XDnnZCQ4Pf2JSXB0Uf7yeC6dTBjhn99n+aoFan5lADWYmlpaTz00EN06tSJxo0bY2YlLlu2bOHFF1/EOcdVV121135GjhyJmbFy5UrS0tKIi4sLvnbatGnBen379iUpKYl58+ZV5ccUkf30008wcKDf4/fYY/4YfhdfDHPmwC+/wKhRcPjh0Y5SRCJJdwHXUlu2bOH8889n5cqVnHzyyQwePJisrCzeeustNm3aRN26dUlISKBFixYceuihzJs3j7i4OM4888y99nXaaafRv39/Xn75Zc4++2wuvvji4Lbzzz8/+Pycc84B4OOPP6Zbt26V/yErQVpaGr/88gsAeXl5JCUlkZiYSPPmzUlISIhydCKRFQj4PX3vvOOX69SBq66Cu+/2B2cWkdpLCWAtdfXVV7Ny5UruvvtuJkyYgOVPlHnXXXfRrl07cnNz+eqrr2jRogXp6ekkJibSvn37Em/+uPLKK9m5cycvv/wy/fv3Z9CgQSW+5+mnnw74gymXZ9KkSezcuTPsz9OxY0d69+4ddv19tWTJEi644IJgeezYsYwdO5b+/fszderUSn9/kaqwcSM8+CA8/7x/o0f9+n4P4IgR/vy6IlL7xUwCWFMmCi8+VdK++Pjjj/nkk08455xzeOSRR4LJH0Dr1q0577zzmDdvHomJiXTt2pUNGzaQm5vL4WWc4ym4AeTUMroFmjZtSoMGDUgKHRisFJMmTWLt2rVhf6b+/ftXSQLoeR4uEj8EkWpo1y745z/907y7d/s9fn/7G4wdC61aRTs6EalKMZMAxpKC6/KGDx9OnRJu0WvatCngn+IE2LZtGwDNypiX6dtvv6Vu3bqcdNJJZb538+bN2bx5c7kxrlmzptw6IhIZeXkwZQrcdx8kJ/vrevf2b+5o3z6qoYlIlMRMAhhLnTqff/45derUoXv37iVuX79+PQDHHnssQPCu38zMzBLr79mzhx9++IETTjiB+vXrl/neGRkZpd5FLCJV7/vvYfBgf6BmgHPOgUcf9YdwEZHYFTMJYKzIy8tj7dq1HHrooSVez7d582YWL17M0UcfTdu2bQE49NBDgcKewOJ+/PFHMjMzyzz9W/DeO3fu5Oijjy43zkhdA2g15dx+OXTaWSItPd2/zu+xx/zr/A4/3B+77y9/qTmXxIhI5VECWMsUJESpqank5eXtdQr40UcfJS8vj5tuuim47vDDD+eQQw4hEAiUuM/ExEQAOnXqVOZ7BwIBnHN07Nix3DgjdQ2gEieRvX3wAQwd6s/SYeY///vfIf/qDxERjQNY25gZp5xyCunp6bzxxhtFtr399ttMmjSJ448/nttvv73Ia7p06UJycnJwCJRQBT2DTZo0KfO9v/rqK4Aid9GWZs2aNTjnwl5q0x24a9as4b///W+0w5BaKCUFrrsO/vQnP/nr2BG++gqeeELJn4gUpR7AWmjMmDH8+c9/ZuDAgcyePZvWrVuzePFi5s2bR7t27fjoo49o0KBBkdf06dOHd955hzlz5gSvDSxQMPXb6NGjWb58OQ0bNuTEE0/kL3/5S5F6c+fOJS4ujssuu6xyP2ANN2fOHJKTk3WcJKI+/9xP/tauhQMO8Hv8brsN4vUtLyIlUA9gLdS7d2/effddOnfuzIwZM5g0aRJbt27l4Ycf5ttvvy3xGr0+ffrQsmVLXnnllb22denShSeeeIKGDRvyxBNP8OCDDwZPCxdISUnhvffe49JLL6V169aV9dFqvAULFjBq1CimTp1Kx44dSUlJiXZIUsPl5Ph393qen/yddhosWwZ33KHkT0RKpwSwlrrsssv48ssvSU9PZ/fu3SQmJnLvvffSqFGjEuvXq1eP22+/nW+++YZly5bttX3o0KEEAgEyMzNxzvHwww8X2f7KK6+QmZnJnXfeWSmfpywLFy6kV69etGrVCjOr1qeLzz//fE4++WTmzp1LYmJicEgekX3x88/+Xb0PP+yPdDBqFHz5JRx3XLQjE5HqTgmgBA0fPpyEhATGjBlToddlZGTwyCOP0KdPH84777xKiq50aWlpdOjQgcmTJ+/TEDQDBgzggQceiFg8HTp0KHFZt24d4F8D2KZNm4i9n8SmN97wr/FbvBgSEmD+fH9cv3r1oh2ZiNQEOkEgQQ0aNODVV1/ls88+Iz09vcRhZEqyZs0aBg0axIABAyo3wFL07NmTnj17AlR6DBs2bGDUqFF8+OGH5ObmctFFF/HUU0/RsmXLYJ3ly5eX+vr169dz2GGH1Zrha6Tq7dkDI0f6w7sA9O0LTz8NBx0U1bBEpIZRD6AU0aVLF8aOHRt28gfQvn17HnjggVrfq/Xbb79x6qmn0qpVKxYtWsT8+fNJTk5m8ODBYe9j3bp1HHHEEZUYpdRmW7fCJZf4yV98PDz5JLz+upI/Eam4sBJAM2tuZu+aWbqZrTWzq0up94yZpYUsWWaWGrJ9vpllhmwveeA5kWpo8ODB3HDDDTzyyCO0b9+ejh07cv/99/PJJ5+EvY8TTjiBtWvXctJJJ/HDDz9UYrRS2yxd6t/g8dln0LKl/3jLLRrUWUT2TbingJ8EsoGWQEfgQzP7zjm3IrSSc24wEOwOMbOpQF6xfQ11zj2/rwGL7K/x48czfvz4YDkrKwszY+LEicF1s2bNKnI9Y1JSEnPnzuXzzz/n8ccfD67Pzc3lwAMPDPu9mzZtytKlS/fzE0iseflluOkmyMqCM8+Et9+GVq2iHZWI1GTlJoBm1hDoA3RwzqUBi8zsfeA64J4wXndphGIViYjBgwdz5ZVXBssjR46kVatW3HbbbcF1rYr9dU1MTKRJkyYlJm/1dNW9VJK8PBg9GiZM8Ms33QSTJ0M5U3KLiJQrnB7APwC5zrlVIeu+A84v53V9gK3AwmLrHzGzCUAAGO2cm1/Si81sEDAIICEhIYwwRcLTvHlzmjdvHiw3btyY5s2b7zUAdqi6deuSnp7OYYcdVupQOiKRlJ0N118Pr70GcXH+9X4hMziKiOyXcK4BbAQUH602BWhczuv6A6+4opO1jgTaAq2A54CZZnZMSS92zj3nnOvsnOt8yCGHhBGmxKq0tDQSExNJTEwkLy+PpKQkEhMTSUpKith7nHnmmTRr1ozrrruOZcuW8euvv/Lxxx8zZMgQ8vKKX+Ugsn927oTu3f3kr1Ejf25fJX8iEknhJIBpQPFJYJsAqSXUBcDMWuP3EBaZVsI597VzLtU5l+Wcexn4AuhZsZBFilqyZAmdOnWiU6dOZGRkMHbsWDp16lTh8QzL0qxZM2bNmkVKSgoXXHABHTt2ZMSIERx55JHUqaOb6SVy1q2Dc8/1b/I47DBYuNBPBkVEIimcU8CrgHgza+ec+zl/3SnAijJe0w/40jm3upx9O0D3sMl+8TyPoh3NFRPuzCGdO3fm008/3ef3ESnPd99Bz57w++/Qvj3MmgVHHRXtqESkNiq368I5lw7MAB4ys4Zmdg5wGfBqGS/rB0wNXWFmB5lZNzNrYGbxZnYN0AWYs8/Ri4jUEosWQZcufvLXpQt88YWSPxGpPOGeu7oFOADYArwB3OycW2FmCfnj+QXv0jCzs4AjgbeK7aMu8Hf8G0OSgVuB3s45jQUoIjFt3jzo1g127YIrroA5c6BZs2hHJSK1WVjjADrntgO9S1ifhH+TSOi6/wF7TSPhnNsKnL5PUYqI1FIffgh9+vhj/A0YAM8/79/1KyJSmXT1uohIlLz9NvTu7Sd/t9wCL7yg5E9EqoYSQBGRKHj1VbjqKtizB0aMgH//G3RDuYhUlVr3dbM/d4OKVDdqz7XTc89B//7+TB9jx8Kjj2pOXxGpWuHOBVwjxMXFkZOTo6m5pNbIyckhTucEa5Xnny8c1Pkf/4C7745uPCISm2pVD2Djxo3ZtWtXtMMQiZhdu3bRuHF5k+5ITfHKKzBokP/8sceU/IlI9NSqBLB58+bs2LGD5ORksrOzdfpMaiTnHNnZ2SQnJ7Njx44i8xZLzfWf/8DAgeAcTJgAw4dHOyIRiWW16hRw/fr1SUhIYPv27axZs4bc3NxohySyT+Li4mjcuDEJCQnUr18/2uHIfnrnHbj2Wv+av4cegpEjox2RiMS6WpUAgp8EHn744Rx++OHRDkVEhJkzoW9fyM2F0aPh/vujHZGISC07BSwiUp3MmePP7FEw1Mu4cdGOSETEpwRQRKQSLFoEl18O2dlw220a6kVEqhclgCIiEfbdd3DppZCRATfcAJMmKfkTkepFCaCISAT98gt06wYpKf4cv88+q+RPRKofJYAiIhGyYQNcfDFs3gxdu8Jrr2luXxGpnpQAiohEwPbtfs/fmjXwxz/Cu++CRvARkepKCaCIyH5KS4OePWHFCjjhBPjoI2jUKNpRiYiUTgmgiMh+yM72h3r5+ms46iiYOxcOPjjaUYmIlE0JoIjIPsrL8+/ynTMHDjkEPv4YWrWKdlQiIuVTAigiso9GjYJp06BhQ/+0b7t20Y5IRCQ8SgBFRPbBpEn+4M7x8TBjBnTuHO2IRETCpwRQRKSC/vMfGD7cf/7SS3DJJdGNR0SkopQAiohUwCefQL9+/vN//hOuvTa68YiI7AslgCIiYVq2zJ/fNyfH7wG8885oRyQism/CSgDNrLmZvWtm6Wa21syuLqXeADPLNbO0kMWr6H5ERKqbzMzD6NkTUlPhr3+FiRM1xZuI1FzxYdZ7EsgGWgIdgQ/N7Dvn3IoS6v7POXduBPYjIlIt5OQ04fvvHyUjAy66CKZOhTo6fyIiNVi5X2Fm1hDoA9zvnEtzzi0C3geuq8gbRWo/IiJVKSMDli8fT0ZGAiefDO+8A/XqRTsqEZH9E87/sH8Acp1zq0LWfQecWEr9TmaWbGarzOx+MyvoZazofoICgQBTp04FICcnB8/zmDZtGgC7d+/G8zymT58OQEpKCp7nMWPGDACSk5PxPI+ZM2cCsGnTJjzPY/bs2QCsW7cOz/OYN28eAKtXr8bzPBYsWBB8b8/z+PLLLwFYvnw5nuexePFiABITE/E8j8TERAAWL16M53ksX74cgC+//BLP8wgEAgAsWLAAz/NYvXo1APPmzcPzPNatWwfA7Nmz8TyPTZs2ATBz5kw8zyM5ORmAGTNm4HkeKSkpAEyfPh3P89i9ezcA06ZNw/M8cnJyAJg6dSqe5wWP5ZQpU+jatWuw/NRTT9GjR49gefLkyfTq1StYnjhxIn369AmWJ0yYQN++fYPlcePGcW3IVfBjxoxh4MCBwfKoUaMYNGhQsDxixAiGDBkSLA8bNoxhw4YFy0OGDGHEiBHB8qBBgxg1alSwPHDgQMaMGRMsX3vttYwbNy5Y7tu3LxMmTAiW+/Tpw8SJE4PlXr16MXny5GC5R48ePPXUU8Fy165dmTJlSrDseZ7aXgy3vZEj7+Wvf4VduzpQp856LrzwnzRt6m9X21PbK6DvPbW9qmp7kRTOKeBGQEqxdSlA4xLqLgQ6AGvxE7vpwB7gkQruBzMbBAwCqK8Z1UWkijkHH3/ci2XLID5+F02b/pXGjS+IdlgiIhFhzrmyK5h1Ar5wzh0Ysu5OwHPO/amc1/YF7nLOnbY/++ncubNbsmRJ+Z9GRCRCxo+H0aOhfn1o3/5Wmjb9gfnz50c7LBGJUWa21DkXsSHnwzkFvAqIN7PQSY5OAcK5ccMBBffJ7c9+RESqzMsv+8mfGbz2GjRt+kO0QxIRiahyE0DnXDowA3jIzBqa2TnAZcCrxeuaWQ8za5n//HjgfuC/Fd2PiEi0zJoFN9zgP588GUIuxxERqTXCHcjgFuAAYAvwBnCzc26FmSXkj/WXkF/vIuB7M0sHPsJP+MaXt58IfA4Rkf32zTdwxRWQmwujRsGtt0Y7IhGRyhHWOIDOue1A7xLWJ+Hf3FFQHgGMKF6vvP2IiETbqlXwf/8Hu3dD//7w8MPRjkhEpPJoKFMRiXmbNkG3bpCcDD16wJQpmuVDRGo3JYAiEtN27fKTvjVr4PTT4a23oG7daEclIlK5lACKSMzKyoI//xkSE6FdO/jwQ2jYMNpRiYhUPiWAIhKTcnPhmmvgk0/gsMNgzhw45JBoRyUiUjWUAIpIzHEObrrJn9e3aVN/6Jejj452VCIiVUcJoIjEnHvugRdegAMOgA8+gI4dox2RiEjVUgIoIjHl0Uf9JT7e7wE899xoRyQiUvWUAIpIzJgyBUaO9Id4eeUV/+5fEZFYpARQRGLC22/D4MH+8yefhL/+NbrxiIhEkxJAEan1PvoIrr4a8vJg3Di4+eZoRyQiEl1KAEWkVps71x/rLycH7rgDRo+OdkQiItGnBFBEaq3PPoPLLvMHfB46FCZO1BRvIiKgBFBEaqlFi+DSSyEzE/72N5g8WcmfiEgBJYAiUut8/TX07Am7d8OAAfDMM1BH33YiIkH6ShSRWmXpUujWDVJT/Rs/nn9eyZ+ISHH6WhSRWuObb+DiiyElBa64Al5+GeLioh2ViEj1owRQRGqFhQuha1fYsQMuvxxef92f7UNERPamBFBEary5c6F798LTvm++CXXrRjsqEZHqSwmgiNRo778Pf/oTZGTADTf4U7yp509EpGxKAEWkxpo+Hfr0gexsuPVWeO45XfMnIhIOJYAiUiO99JJ/unfPHhg50h/nT3f7ioiER1+XIlKjOOfP53v99f7cvg89BI88okGeRUQqQlfKiEiNkZMDt9zij+1nBo8/7k/xJiIiFRNWD6CZNTezd80s3czWmtnVpdTrb2ZLzWyXma03s0fNLD5k+3wzyzSztPwlEKkPIiK1W1oa9OrlJ38NGsCMGUr+RET2VbingJ8EsoGWwDXA02Z2Ygn1DgSGAS2AM4CLgBHF6gx1zjXKX47bp6hFJKZs2gTnnw+zZ0OLFvDZZ9C7d7SjEhGpuco9BWxmDYE+QAfnXBqwyMzeB64D7gmt65x7OqS4wcxeAy6IYLwiEmN+/NGf13ftWjjmGD8JPPbYaEclIlKzhdMD+Acg1zm3KmTdd0BJPYDFdQFWFFv3iJklm9kXZuaV9kIzG2RmS8xsydatW8N4KxGpbWbMgDPO8JO/M86A//1PyZ+ISCSEkwA2AlKKrUsBGpf1IjMbCHQGJoasHgm0BVoBzwEzzeyYkl7vnHvOOdfZOdf5kEMOCSNMEaktcnNh9Gh/jL+0NOjbFz79FPRVICISGeEkgGlAk2LrmgCppb3AzHoDE4AezrnkgvXOua+dc6nOuSzn3MvAF0DPCkctIrXWjh1w6aUwfrw/rt+//uXP63vggdGOTESk9ghnGJhVQLyZtXPO/Zy/7hT2PrULgJl1B6YA/+ec+6GcfTtAo3eJCADffw+XXw6rV/s3e0yfDhdeGO2oRERqn3J7AJ1z6cAM4CEza2hm5wCXAa8Wr2tmFwKvAX2cc98U23aQmXUzswZmFm9m1+BfIzgnEh9ERGou52DqVDjrLD/5O/VUWLJEyZ+ISGUJdxiYW4ADgC3AG8DNzrkVZpaQP55fQn69+4GmwEchY/3Nyt9WF/g7sBVIBm4FejvnNBagSAzbvh2uvBIGDoTdu6FfP1i0CI46KtqRiYjUXmHNBOKc2w70LmF9Ev5NIgXlUod8cc5tBU6veIgiUlt9+qmf8G3YAI0awb//7Zc1rZuISOXSXMAiUuWysuCuu6BrVz/5O+ssSEyE/v2V/ImIVAUlgCJSpZYtgzPPhIkT/bt8H3gAFi70B3kWEZGqEdYpYBGR/ZWaCmPGwOOPQ14etG0Lr73mJ4MiIlK11AMoIpXuvffghBNg0iS/PGyYf8pXyZ+ISHSoB1BEKk1SEtx6K7z/vl/u3BmefdYf5kVERKJHPYAiEnG7dsH990P79n7y17ixf+r3q6+U/ImIVAfqARSRiMnOhmeegXHjIDl/EsgrrvBP/bZqFdXQREQkhBJAEdlveXn+tG2jR8Nvv/nrzjkHHn0Uzj47urGJiMjelACKyD7bswfeeQcmTPBv6gD/tO+ECfCnP2lMPxGR6koJoIhUWEaGP3fvxIn+3L0ARxwBDz4IAwZAvL5ZRESqNX1Ni0jYduyAp57yb+jYssVfd8wx/qwe/ftDgwbRjU9ERMKjBFBEyuQcfPEFTJkCb74JmZn++lNPhZEjoU8fiIuLbowiIlIxSgBFpETbtsGrr8Jzz8FPPxWuv+QSv8fvoot0jZ+ISE2lBFBEgtLT4aOP/J6+mTMhK8tf37IlXH893HCD5uwVEakNlACKxLjdu2HWLD/p++ADvwx+71737jBoEFx6KdStG904RUQkcpQAisSgpCSYPdtf5s71e/4KnHkmXHmlP4Bz69bRi1FERCqPEkCRGLB7t38jR0HS9+OPRbf/8Y+FSd9RR0UnRhERqTpKAEVqoW3bYNEif/n8c1i61B+0uUDjxtC1q3+Kt3t3SEiIXqwiIlL1lACK1HBpaf4sHEuX+suSJUXv2gWoU8cftuXii/2E7+yzoV69qIQrIiLVgBJAkRpizx749Vf/9O2PP8KKFbBsGQQC/lh9oRo0gDPOgHPPhfPOg7POgiZNohO3iIhUP0oARaqR3FxYt85P9EKXQABWrYLs7L1fU7cudOgAp53m9/KddhqccgrUr1/18YuISM2gBFCkimRn+9OnbdoEGzf6iV7osn69/5iTU/o+2rSBE04oXE4+2U/+lOyJiEhFKAEU2QfZ2ZCSAjt3+vPj7tzp33iRnOwvBc+3boXNm/2kb9u28PZ9xBH+YMtt2/qPxxwD7dpB+/bQqFFlfioREYkVYSWAZtYceAG4BEgGRjnnXi+l7nBgJHAA8A5ws3Muq6L7EdlXzvm9aFlZRZfMTMjI2HvZvdsfB6/4kpYGqamFy65d/mNKSuFgyRVRpw4ceigcdpi/tG7tL0ceWfi8dWs48MDIHxMREZFQ4fYAPglkAy2BjsCHZvadc25FaCUz6wbcA1wI/A68CzyYvy7s/RSXlgYLF4YXaPGL4fe1fknrK1K3+PqKPK/IY8ESWi7teThLXl7J5dDH0p7n5hauK1hycwuX4uWCZc+eos8LygXPc3IKl+Ll7OySl4q2g4qKi4NmzeCggwqXgw+GFi0KHwueFyR8Bx/sv05ERCTazJXzl9LMGgI7gA7OuVX5614FNjjn7ilW93VgjXPu3vzyRcBrzrnDKrKfvWPo7GDJPn1AiU1mezDLoU6d7Pyl4HlWyLos4uKy8h8z8h8z85/7j/Hxu4mLK1zi4zOIj0+jTp0MzKL9KaWqJCYmAtCxY8eoxiEisWvBggVLnXOdI7W/cHoA/wDkFiRt+b4Dzi+h7onAf4vVa2lmBwMJFdgPZjYIGOQ/b0+TJt+FEWqBSHX/7L0fs9L2Hc57FtYpup+SXuuK1SteJ3R70X2V/BpXrG5J5bwSthWu9x9D17kidc3yMMstst1/zMvfVvS5WW5+/b3XhS6QS506uflJnb8UlOvUyclP9PaEPO4J+SwiIiJSXDgJYCMgpdi6FKBxGHULnjeu4H5wzj0HPAfQuXNnt2TJKWGEKiISeZ7nATB//vyoxiEiscsifNqpThh10oDiQ8g2AVLDqFvwPLWC+xERERGRShJOArgKiDezdiHrTgFKunFjRf620HqbnXPbKrgfEREREakk5SaAzrl0YAbwkJk1NLNzgMuAV0uo/gpwg5mdYGbNgPuAqfuwHxERERGpJOH0AALcgj+u3xbgDfyx/VaYWYKZpZlZAoBzbjbwKPAZsDZ/GVvefiLySUREREQkLGGNA+ic2w70LmF9Ev7NHaHrHgMeq8h+RERERKTqhNsDKCIiIiK1hBJAERERkRijBFBEREQkxigBFBEREYkxSgBFREREYowSQBEREZEYY865aMdQLjNLBQLRjqMaawEkRzuIak7HqGw6PuXTMSqbjk/ZdHzKp2NUtuOcc40jtbOwxgGsBgLOuc7RDqK6MrMlOj5l0zEqm45P+XSMyqbjUzYdn/LpGJXNzJZEcn86BSwiIiISY5QAioiIiMSYmpIAPhftAKo5HZ/y6RiVTcenfDpGZdPxKZuOT/l0jMoW0eNTI24CEREREZHIqSk9gCIiIiISIUoARURERGKMEkARERGRGFMtEkAzG2pmS8wsy8ymlrD9IjNbaWa7zewzMzuqjH01N7N3zSzdzNaa2dWVGnwUmFlasSXXzJ4ope6A/O2h9b2qjbhqmdl8M8sM+bxlDiJuZsPNbJOZpZjZi2ZWv6pijQYzq29mL+T/fqSa2TIz61FG/ZhoQxX57lCbKb3NxEp7KUlFvntisA3p71YxZeU+VZH3VIsEEPgd+DvwYvENZtYCmAHcDzQHlgDTy9jXk0A20BK4BnjazE6MdMDR5JxrVLDgf84M4K0yXvK/0Nc45+ZXSaDRNTTk8x5XWiUz6wbcA1wEtAHaAg9WTYhREw+sA84HmuL/br1pZm3KeE0stKGwvjvUZsJqM7HQXkpT7ndPLLYh/d0qUYm5T1XlPdUiAXTOzXDOvQdsK2Hzn4EVzrm3nHOZwAPAKWZ2fPGKZtYQ6APc75xLc84tAt4Hrqu04KPvCmAL8Hm0A6mh+gMvOOdWOOd2AOOAAdENqXI559Kdcw8459Y45/Kccx8AvwGnRTu2aKngd4fajNrM/oq5NlSM/m5RZu5TJXlPtUgAy3Ei8F1BwTmXDvyav764PwC5zrlVIeu+K6VubdEfeMWVPZ5PJzNLNrNVZna/mdWUKQD3xyP5n/mLck4dFGlf+c9bmtnBlRlcdWJmLfF/d1aUUa22t6GKfHeozZTfZmp7eylLON89sd6G9HerbFWS99SEBLARkFJsXQpQ0oTIFalb45lZAv4pmZfLqLYQ6AAciv9fwl+Buyo/uqgaiX9KpRX+wJkzzeyYUuoWbzMFz2tlmynOzOoCrwEvO+dWllItFtrQ/nzPqM0UFQvtpTThfvfEbBvS362wVEneU+kJYP5Fsa6UZVEYu0gDmhRb1wRI3c+61VIFj1c/YJFz7rfS9uecW+2c+y3/tM0PwEP43e81UjjHxzn3tXMu1TmX5Zx7GfgC6FnKLou3mYLnNabNFBduGzKzOsCr+NeODC1tf7WtDZVif75nanybCVc4bSZG2kuJKvDdE7NtiBj8u7UPqiTvqfQE0DnnOeeslOXcMHaxAjiloJB/vvsYSj71sAqIN7N2IetOKaVutVTB49WPsv+LKvEtAItMtFVvH9tTWZ+5SPvKf77ZOVfS9ag1QjjHyMwMeAH/ouE+zrmcirwFNbgNlaIi3x21rs2EYz/aTG1sL+Eq7bPHZBvKF3N/t/ZBleQ91eIUsJnFm1kDIA6IM7MGIef73wU6mFmf/DpjgO9LOvWQf558BvCQmTU0s3OAy/D/Y61VzOxs/NMMZd1FhZn1yL9eh/wLSO8H/lv5EUaHmR1kZt0K2pCZXQN0AeaU8pJXgBvM7AQzawbcB0ytonCj6WmgPfAn51xGWRVjoQ1V8LtDbaaMNhML7aUkFfzuick2pL9bRZWR+1RN3uOci/qCf4eLK7Y8ELK9K7AS/7bx+UCbkG33ArNCys2B94B0IAm4Otqfr5KO2bPAqyWsT8DvEk7IL08ENucfj9X4Xel1ox1/JR6XQ4DF+N3fO4GvgItLOz756+7IP0a7gJeA+tH+HJV8jI7K/x3LzD8WBcs1sdyGSvvuUJspu83Eansp4RiV+t2jNhT8zPq7VfRzP0ApuQ9VkPdY/otFREREJEZUi1PAIiIiIlJ1lACKiIiIxBglgCIiIiIxRgmgiIiISIxRAigiIiISY5QAioiIiMQYJYAiIiIiMUYJoIhIGfLnVv53tOMQEYkkJYAiIiIiMUYzgYiIlMLMpgL9i60+2jm3puqjERGJHCWAIiKlMLOmwCz8OTnvzV+91TmXG72oRET2X3y0AxARqa6ccylmlg3sds5tinY8IiKRomsARURERGKMEkARERGRGKMEUESkbNlAXLSDEBGJJCWAIiJlWwP80czamFkLM9P3pojUePoiExEp20T8XsAfga1AQnTDERHZfxoGRkRERCTGqAdQREREJMYoARQRERGJMUoARURERGKMEkARERGRGKMEUERERCTGKAEUERERiTFKAEVERERijBJAERERkRjz/wG3/B6/S/i5+QAAAABJRU5ErkJggg==)]

逻辑回归模型预测
y ^ = { 0 , 如果 p ^ < 0.5 1 , 如果 p ^ > = 0.5 注意，当 t < 0 时， σ ( t ) < 0.5 ; t > 0 时， σ ( t ) > = 0.5. 如果 x T Θ 是正类，逻辑回归模型预测结果是 1 如果是负类，则预测为 0 \widehat{y} =

$$\begin{cases} 0,如果\widehat{p}<0.5\\ 1,如果\widehat{p}>=0.5 \end{cases}$$ \\ 注意，当t<0时，\sigma(t)<0.5;t>0时，\sigma(t)>=0.5.\\如果x^T\Theta是正类，逻辑回归模型预测结果是1\\如果是负类，则预测为0 y ​={0,如果p ​<0.51,如果p ​>=0.5​注意，当t<0时，σ(t)<0.5;t>0时，σ(t)>=0.5.如果xTΘ是正类，逻辑回归模型预测结果是1如果是负类，则预测为0

训练和成本函数

单个训练实例的成本函数
c ( Θ ) = { − l o g ( p ^ ) ,       如果 y = 1 − l o g ( 1 − p ^ ) , 如果 y = 0 c(\Theta) =

$$\begin{cases} -log(\widehat{p}),\ \ \ \ \ \ 如果y = 1\\ -log(1-\widehat{p}),如果y = 0 \end{cases}$$ c(Θ)={−log(p ​),      如果y=1−log(1−p ​),如果y=0​
逻辑回归成本函数(对数损失)
$$J(\Theta )=-\frac{1}{m}\sum _{i=1}^m[log({\hat{p}}^{(i)}+(1-y^i)log(1-{\hat{p}}^{(i)}))]$$
逻辑成本函数偏导数
$$\frac{\partial }{\partial {\Theta }_j}J(\Theta )=\frac{1}{m}\sum _{i=1}^m(\sigma ({\Theta }^T{x}^{(i)})-y^{(i)})x_j^{(i)}$$

决策边界

'''决策边界'''
iris = datasets.load_iris()
x = iris['data'][:,3:]
y = (iris['target']==2).astype(np.int_)
log_reg = LogisticRegression()
log_reg.fit(x,y)
#画图展示模型估算出的概率
x_new = np.linspace(0,3,1000).reshape(-1,1)
y_proba = log_reg.predict_proba(x_new)
plt.plot(x_new,y_proba[:,1],'g-',label = 'Iris virginica')
plt.plot(x_new,y_proba[:,0],'b--',label = 'Not Iris virginica')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CfEOzzhj-1658889211624)(data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAXcAAAD7CAYAAACRxdTpAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAw60lEQVR4nO3dd3hUVfrA8e+bHhICASJFQECR3hOlIyq6NnBFXAVRFMEFdBUVBZEqIrhiWX+ADUVBcS00OyIKoojAKr1Il95DEtJzfn+chIQQyAAzuVPez/PcZ+7ce2bue7nhnTNnzj1HjDEopZTyL0FOB6CUUsr9NLkrpZQf0uSulFJ+SJO7Ukr5IU3uSinlh0KcDgCgQoUKpkaNGk6HoZRSPmXFihWHjDFxRe3ziuReo0YNli9f7nQYSinlU0Rkx5n2abOMUkr5IU3uSinlhzS5K6WUH9LkrpRSfkiTu1JK+SGXkruIPCQiy0UkXUSmFlN2oIjsE5FEEXlHRMLdEqlSSimXuVpz3wOMAd45WyERuR4YDFwD1ABqAaMuID6llFLnwaV+7saYmQAiEg9UPUvRe4Epxpi1ueWfBT7AJnyPeOUVmD0bgoPzl6Ag+1irlt2fp1cvMObUsnnlu3WD9u1tuRUrYNYsuz0kBMLDISzMLuHh9n1Ccv/lliyB5OTTy4SFQWwsVKjgqTNXSnmzHJNDelY6qVmppGamFvmYkZ1BTHgMV9W4yu3Hd/dNTA2AOQWerwQqikh5Y8zhggVFpC/QF6B69ernfcCNG2HhwqL3NW586vNp0yAnp+iydevmJ/c//oDnnjvzMXv1yl8fOBCWLj1zuXfftetr18KVV0JUlF2io/PXo6Jg/HgbA8CPP8KmTfbDoeBSrhzExNgPHaWUZ+SYHBLTEjl44iCHThzi0IlDHEs7RmJaIsfTj+cvGcdPeZ6UnsSJzBMnk3d6drpLx2tZtSVLei9x+3m4O7lHA4kFnuetlwZOSe7GmDeBNwHi4+PPe8aQgQPhjjsgOzt/ycmxj6VLn1p26tRTyxUs365dfrnmzeHZZ+2+zEy7pKdDRoZ9DA7OL5uQYBN13r6MjPz1SpXyyyUnQ0qKXYoyYkT++gcfwNtvF12uYUNYvdquGwMPPmi/HVSubI938cVQs6ZdF3H5n1Epv5eRncHepL3sOr6LXcd3sTtp98nH/cn7TybzwycOk22y3XLM8OBwIkMjiQyJPO0xIiSC8JBw6lWo55ZjFebu5J4MxBR4nree5ObjnHT55XZxRc+erpVr1swurnjtNdfKJSRAYmJ+gs9b8pL+pZfml23f3ibuo0fhyBH7mLcU/sB4662ijxcRYb813Hmnfb5mDWzdCvXr2+Rf8ANKKX+RnJHMn4f/ZPORzfnLUfu4J2mPy+9TJrwMFUpVOLnERsZSJrwMMeExZ1xKh5WmVGipk8k7PCScIHHua7a7k/taoAnwce7zJsD+wk0ygSgoyDapxMQUX7ZnzzN/EBVsVgoOhjffhH37YO9eu+zaBdu2weHDthknzyefwOjRdj0iwjYB1a8PDRpAfDxcd935n5tSJS3H5LDlyBZW7V9llwOrWL1/NVuObjnja4IkiMrRlakaU5WqMVW5uPTFJ9crRVciLiqOCqUqUC6yHGHBYSV4Np7hUnIXkZDcssFAsIhEAFnGmKxCRd8HporIB8Be4BlgqvvCVQXb20uVgj59ii53/Lj9YTdP7do2ga9bZz8A/vjDLmC/+WzcmF924kTbNBUfD6Gh7j4Dpc5dYloiS3cv5dddv7Jk1xKW7lrK0bSjp5ULDQrlsnKXUbt8bS6LzX0sdxmXlbuMqjFVCQnyirESS4S4MkG2iIwERhTaPArbNXIdUN8YszO37GPAU0Ak8BnwT2PMWX9ZiI+PNzoqZMlJTIT1622iX70aypeHZ56x+/bts+33YH/obdcOrroKOnaEFi20OUeVjLSsNH7e+TPzt85n/rb5rNizAsOpuapydGWaVW5Go4sa0bhiYxpXbEyd8nUIDQ6cGomIrDDGxBe5z5Xk7mma3L3HX3/BmDG2B1LB2jxAXBx89ZWt0SvlbvuT9zNn4xxmbZjFj9t/JC0r7eS+0KBQmlduTquqrWhVrRWtqraiakxVJMB7DZwtuQfOdxTlkmrV4I037PqePTbJ//ADzJ8Pu3dDnTr5ZV991f7A27kzREY6E6/ybfuS9zFj9QxmbpjJzzt/PqV23qRiE66tdS2danWibfW2RIVFORip79Gau3KJMbBzJ1xyiX2elQUVK9rePDExcPvtcM89tqdPgFemVDHSstL4fOPnvLfyPb7Z/M3JbodhwWF0qtWJv9f9OzdffjMVoys6HKn302YZ5Xbp6baGP20aFLx0devCQw/ZRF/4PgMV2P5K/IuJyyby1v/e4kjqEQBCgkK4qfZN3NXwLm6ofQMx4S50J1MnaXJXHrV+PUyfbm8S25PblfjXX+0duUot+WsJL//6MjPXzzxZS29aqSm9mvSie6PuxEUVOQWocoEmd1UiMjPtmDwLFsDrr+dvnzgRbrzR3jylAsfinYsZ+eNIvt/2PWBr6bfXv51HrnyEllVbOhydf9Dkrhzzxx/2bt/gYLj3XjusQ5UqTkelPOnXXb8y7IdhzN86H4CY8BgGJAxgQMIALo652OHo/MvZkrsOQaU8qmxZm9QB3nnH3kw1atSZx9hRvmvX8V30mNmDVlNaMX/rfGLCYxjefjjbH9nO2GvGamIvYZrclUfVqGHb4jdsgK5d4cQJGDnS3hU7Y4bDwSm3SM1MZfTC0Vz+2uV8uPpDwoPDGdJ2CNse2caojqOIjYx1OsSApMldlYjLLoNPP7X95lu0sD+8zpvndFTqQi3asYgmrzdhxI8jSM1KpVv9bmx4aANjrxlLuchyxb+B8hi9iUmVqPbt4bff4L337M1PeQ4csEMX61j1viEpPYnB8wczafkkABrENWDSTZNof0l7hyNTeTS5qxIXFAT33Zf/PDUVrr7ajkX/3nunDmusvM/SXUu567O72HZsGyFBIQxtN5Sn2z3tFyMp+hOtJynHbdxoByybN8/OnvXll05HpIqSY3IYv3g8bd9ty7Zj22heuTn/6/s/Rl41UhO7F9LkrhzXtCmsWgXXXAMHD8LNN8PgwXYmLOUdDp84zA0f3MDg7weTlZPFYy0fY0nvJTSq2Mjp0NQZaHJXXqFKFVtzHz/e9okfP94m+aOnD9mtStiaA2tIeCuBeVvmUaFUBb7s/iUTrp+gtXUvp8ldeY2gIHjySfjuOzvG/DffwJw5xb9Oec6cDXNoNaUV245tI75KPL8/+Ds31r7R6bCUC/QHVeV1Ona0g5F9+GH+DVCq5E34ZQJPfPcEAN0bdeftW94mMlTHdvYVWnNXXqlGDXj66fzhg7duhdmznYwocBhjePK7J08m9ueveZ7pf5+uid3HaHJXXi8pCf72N7jtNpg82elo/FtWTha95/bm37/8m5CgED647QMGtx0c8DMe+SJN7srrRUfbfvHGQP/+8MorTkfknzKyM+j2STfe/eNdSoWW4vO7Pqd7o+5Oh6XOkyZ35fVEYMiQ/Fr7wIEwYYKzMfmbzOxM7vz0TmZvmE1sRCzze87nb5f9zemw1AXQH1SVz/jnP22PmgcfhCeegJwcGDTI6ah8X1ZOFj1m9mDWhlmUjSjL/Hvm07xyc6fDUhdIa+7Kp/TtC2+/bWvzTz5pZ3xS5y87J5ues3ryybpPiAmPYd7d8zSx+wmtuSuf07s3ZGTA8ePQUif0OW/GGP719b/4aM1HlA4rzbd3f0vCxQlOh6XcRJO78kn9+p363Jj8bpPKNeMWj2PS8kmEB4fzRfcvdOo7P6PNMsrnbdliJ+NevdrpSHzH+yvf5+kFTyMI02+brkP1+iFN7srnTZgAy5bZsWj27XM6Gu/33Zbv6D23NwCv/u1Vbq9/u8MRKU/Q5K583ksvQatWsHMn3HqrHR9eFW3zkc3c8ekdZOVkMaj1IB6+8mGnQ1Ieosld+byICJg1Cy65BJYuhfvvt23w6lRJ6Ul0+agLx9KO0aVOF8ZdO87pkJQHaXJXfqFiRfjiCyhdGj76SO9iLSzH5NBzVk/WHVxHvQr1eP/v7xMk+t/fn+nVVX6jYUOYOtWuDxpkZ3hS1rMLn2XOxjmUjSjLnDvnEBMe43RIysNcSu4iUk5EZolIiojsEJEiB5wQa4yI7BaRRBH5UUQauDdkpc7stttg6FA7VMHllzsdjXf4bst3jFo4iiAJYkbXGdQuX9vpkFQJcLWf+0QgA6gINAW+FJGVxpi1hcp1A+4H2gI7gDHANEBveVMlZswYpyPwHvuS93H3rLsxGEZ2GKnjxQSQYmvuIhIFdAWGGWOSjTGLgblAzyKK1wQWG2O2GmOygelAfXcGrNS52LgRpkxxOgpn5LWzH0g5QMcaHRnabqjTIakS5EqzzOVAtjFmU4FtK4Gimls+Ai4TkctFJBS4F/imqDcVkb4islxElh88ePBc41aqWAcPQny8HY/ml1+cjqbkjVs8jvlb5xNXKo7pt00nOCjY6ZBUCXIluUcDiYW2JQKliyi7F/gJ2AikYptpBhb1psaYN40x8caY+Li4ONcjVspFcXEwYIAdPbJHDzsWTaBY8tcShv8wHID3//4+VUpXcTgiVdJcSe7JQOGf1mOApCLKjgASgGpABDAKWCAipS4kSKXO1+jR0Lw5bN8ODz3kdDQlIyUjhXtm30O2yWZQ60Hazh6gXEnum4AQESn4E3sToPCPqXnb/2uM2WWMyTLGTAVi0XZ35ZCwMDvRdmQkTJtm+8D7uyHfD2Hzkc00vKghz3Z81ulwlEOKTe7GmBRgJjBaRKJEpA3QBdsLprBlQDcRqSgiQSLSEwgFNrszaKXORZ068PLLdn3AANi/39l4POn7rd/z2m+vERIUwvu3vk94SLjTISmHuHoTU38gEjgAzAD6GWPWikh1EUkWkeq55cZjf2z9AziGbW/vaow55s6glTpXfftCp05w4gT89pvT0XhGYloi98+9H4Dh7YfTrHIzhyNSThLjBYNwxMfHm+XLlzsdhvJzO3dCWpr/3tzUZ24f3v79bRKqJPBL718ICdLpGvydiKwwxsQXtU+vvgoY1asXX8ZXLdqxiLd/f5uw4DCm3jpVE7vSsWVU4DHGjkHjL71n0rPS6ft5XwCGtB1C/Tjtv6C05q4C0O7d0L+/Hff91lvh2mudjujCjFs8jo2HN1KnfB2GtB3idDjKS2jNXQWcqlVh2DC7PmAApKc7G8+F2HBoA2MXjwXgjZvf0N4x6iRN7iogPf441K0LmzbBiy86Hc35yTE5PPjFg2RkZ9C7WW861OjgdEjKi2hyVwEpLAwmTrTrY8bAtm3OxnM+pq2cxqIdi7go6iJe6PSC0+EoL6PJXQWsq6+G7t1t98iHH/atqfmOpx/nqflPAfDvTv+mXGQ5hyNS3kaTuwpoL74IMTG25n70qNPRuO7Zhc+yP2U/raq24u7GdzsdjvJC2ltGBbTKlWHBAmjUyDbV+IKNhzby6tJXEYT/3PAfnQtVFUmTuwp4LVo4HYHrjDE8+u2jZOZk0rtZb+KrFHlzolLaLKNUnv377Y1N3jyw2Jd/fsk3m78hJjyGsdeMdToc5cW05q5Urocfhk8+gcxMeOMNp6M5XUZ2BgO/tXPfjLpqFBdFXeRwRMqbac1dqVyjR0NICLz9Nqxc6XQ0p3tj+RtsPrKZuhXqMiBhgNPhKC+nyV2pXHXrQr9+dlq+xx7zrq6RiWmJjF40GoDx144nNDjU4YiUt9PkrlQBI0ZAbKztQfPFF05Hk++Fn1/g0IlDtKvejlsuv8XpcJQP0OSuVAHly+ePO/P005Cd7Ww8ALuO7+KlX18C7A1LIuJwRMoXaHJXqpD+/eGSS2DNGli0yOloYMQPI0jLSqNb/W5cWfVKp8NRPkJ7yyhVSHg4vPUWlC0LCQnOxrJ6/2qmrrSTb2jXR3UuNLkrVYROnZyOwBr8/WByTA4DEgZwWbnLnA5H+RBtllGqGD/9BImJJX/chdsX8tWfX1E6rDTD2g8r+QCUT9PkrtRZPPMMtG9f8mO+G2N45odnAHii9RPERcWVbADK52lyV+osbrzRPr70UskOSzBvyzwW71xM+cjyPNry0ZI7sPIbmtyVOovWraFzZzhxAsaPL5ljGmMY9oNthnmqzVPEhMeUzIGVX9HkrlQxRtsbQ5k8Gfbs8fzxPt/0Ocv2LKNiVEUGXKHDDKjzo8ldqWI0aQJdu9oZm8aN8+yxckzOyVr70+2eplRoKc8eUPktTe5KuWDkSBCxo0Xu2uW543y27jNW7V9F1Ziq9G3R13MHUn5P+7kr5YKGDeHee+3wBJGRnjlGdk42w38cDsAz7Z4hIiTCMwdSAUGTu1IueucdW3v3lA9Xf8iGQxuoWbYm9zW7z3MHUgFBm2WUclHBxO7u4YCzc7JPDuk7osMIwoJ9ZEJX5bVcSu4iUk5EZolIiojsEJHuZylbS0S+EJEkETkkIi+4L1ylnDd9OtSvD9u2ue89P177MZuPbKZWbC16NO7hvjdWAcvVmvtEIAOoCPQAJotIg8KFRCQM+A5YAFQCqgLT3ROqUt5h3jzYsAHGjHHP++WYHMYutoOCDW4zmJAgbS1VF67Y5C4iUUBXYJgxJtkYsxiYC/QsongvYI8x5iVjTIoxJs0Ys8qtESvlsGHDICgI3n8ftm+/8Pf7fOPnrDmwhotLX8w9Te658DdUCtdq7pcD2caYTQW2rQROq7kDLYHtIvJ1bpPMjyLSqKg3FZG+IrJcRJYfPHjw3CNXyiG1a0P37pCVBS9cYKOjMYbnfnoOgEGtBxEeEu6GCJVyLblHA4XHxEsEShdRtipwJ/AfoArwJTAnt7nmFMaYN40x8caY+Lg4HRRJ+ZYhQ+wPrFOmXNhdq99v+55le5YRVyqOPi36uC9AFfBcSe7JQOHBLWKApCLKpgKLjTFfG2MygBeB8kC9C4pSKS9Tv769azUj48JGjMyrtQ9sOVDvRlVu5Upy3wSEiEjtAtuaAGuLKLsK8KI545XynKFD7eNXX9kmmnP1y1+/8OP2HykTXob+Cf3dG5wKeMUmd2NMCjATGC0iUSLSBugCTCui+HSgpYhcKyLBwKPAIWC9+0JWyjs0bQpffw2rVkHIeXRwyau1P3zFw5SJKOPe4FTAc7UrZH8gEjgAzAD6GWPWikh1EUkWkeoAxpiNwN3A68BR7IdA59wmGqX8zt/+BmHncb/R73t/56s/v6JUaCkeafmI+wNTAc+l+oYx5ghwaxHbd2J/cC24bSa2pq9UwDh0CFavho4dXSuf16/9wRYPUqFUBQ9GpgKV3i2h1AXasQMaNLA1+B07oHRR/cgKWH9wPZ+t+4yw4DCeaP1EyQSpAo6OLaPUBbrkEmjeHI4etRN6FGfcz+MwGO5reh9VSlfxfIAqIGlyV8oNnrFzWTNhgp2S70y2H9vOB6s+IFiCearNUyUTnApImtyVcoNOnSAhAQ4cgDffPHO5F35+gWyTTfdG3akZW7PkAlQBR5O7Um4gkl97f/FFSE8/vczepL288/s7CMKQtkNKNkAVcDS5K+UmN98MjRrB7t12ULHCJiyZQHp2OrfVu416cXrTtvIsTe5KuUlQkB1zpmNHqFcodx8+cZjXl78OwNB2Qx2ITgUa7QqplBvdeSfcddfp219d+iopmSnccNkNNKvcrOQDUwFHa+5KuVFRc6weTz/Oa7+9BsDT7Z4u4YhUoNLkrpQHrFoF3brBnDkwadkkjqUdo/0l7Wlbva3ToakAoc0ySnnAwoXw6aewZWs2f/3jJUDb2lXJ0pq7Uh7wwANw0UXw+/+CObS6KfFV4ulUq5PTYakAosldKQ+IjIRHHs0d5P2noQxtNxQpqkFeKQ/R5K6Uh8S0+RAijsKODpQ72NnpcFSA0eSulAdk5WTx6spn4cr/APD8WP2vpkqW/sUp5QGfrP2EzUc2U+P6z4mKMsyfDzt3Oh2VCiTaW0YpN8sxOScn4xh6/T8pX1do1gyqV3c4MBVQNLkr5Wafb/ycNQfWcHHpi+nZuCfhzZ2OSAUibZZRyo2MMScnvh7UehDhIeEn9+XkwIoVTkWmAo0md6XcaP7W+Szbs4y4UnH0adHn5PbMTIiPhyuvhK1bHQxQBQxN7kq5UV5b+8CWAykVWurk9tBQaNwYsrNh/HinolOBRJO7Um7yy1+/8OP2HykTXob+Cf1P2z9kiB1YbOpUO+a7Up6kyV0pNxmzaAwAD1/xMGUiypy2v04duP12yMiwszUp5Uma3JVygxV7VvD15q+JCo3ikZaPnLHc07kj/r7xBhw8WELBqYCkyV0pN8jrIdMvvh8VSlU4Y7mmTeHGGyE1FV55pWRiU4FJk7tSF2jNgTXM2jCLiJAIHm/9eLHlhw6FihWhSpUSCE4FLL2JSakLlFdr79O8D5WiKxVbvnVr2LEDwsOLLarUedOau1IXYOOhjfx3zX8JDQplUOtBLr9OE7vyNE3uSl2AcT+Pw2Do1bQX1cpUO6fXJibC88/DO+94KDgV0LRZRqnztP3YdqatnEawBDO47eBzfv2iRbb3TJUq0KOH1uaVe7lUcxeRciIyS0RSRGSHiHR34TULRMSIiH6AKL80fvF4sk023Rt1p1ZsrXN+/U03QaNGsGcPvPeeBwJUAc3VZpmJQAZQEegBTBaRBmcqLCI90G8Fyo/tPr6bd/54B0EY0nbIeb1HUFB+v/fx4yEry40BqoBXbHIXkSigKzDMGJNsjFkMzAV6nqF8GWAE8KQ7A1XKm7z4y4tkZGdwe/3bqRdX77zfp1s3qF3bDib23/+6MUAV8FypuV8OZBtjNhXYthI4U819LDAZ2He2NxWRviKyXESWH9Rb9ZQP2Z+8nzdWvAHA0HZDL+i9goNhcG5z/dixdlhgpdzBleQeDSQW2pYIlC5cUETigTbAa8W9qTHmTWNMvDEmPi4uzpVYlfIKL/z8AqlZqXSu05kmlZpc8PvdfTdUqwbr1sG8eW4IUClcaxdPBmIKbYsBkgpuEJEgYBLwiDEmS0TcE6FSXmRv0l4mLZ8EwMgOI93ynmFhdiiCsDC4/nq3vKVSLiX3TUCIiNQ2xvyZu60JsLZQuRggHvhvbmIPzt2+S0S6GWN+ckfASjlp3OJxpGWl8fe6f6dZ5WZue9/bbnPbWykFuJDcjTEpIjITGC0iDwBNgS5A60JFE4GCo2VUA34DWgDaqK583u7ju0+2tY+8aqTHjrN1K9Ssacd+V+p8udoVsj8QCRwAZgD9jDFrRaS6iCSLSHVj7ctbyE/o+40xGR6IXakS9fzi50nPTqdb/W40rtjYI8cYPNj2npk1yyNvrwKIS33RjTFHgFuL2L4T+4NrUa/ZDmjdQ/mFvxL/4q3/vYUgjOgwwmPHqVbN9pgZPhy6dLG9aZQ6Hzq2jFIuGPvTWDKyM/hHw3/Q4KIz3r93wR54AKpXh7Vr4eOPPXYYFQA0uStVjO3HtjPl9ykESZBHa+1gx5cZPtyujxihd62q86fJXalijFk0hsycTLo36k7dCnU9frx77oFLL4U//4Tp0z1+OOWnNLkrdRYbDm3g3T/eJViCGd5+eIkcMzQURo6066NG2Qm1lTpXmtyVOouhC4aSY3J4oPkD1C5fu8SOe9dd0KABtGoFSUnFl1eqMB25UakzWLprKTPXzyQyJJLhHUqm1p4nOBiWLYPIyBI9rPIjWnNXqgjGGJ6a/xQAj1z5CFVKl/xs1prY1YXQ5K5UEb7Z/A0LdywkNiKWp9o+5WgsCxbAVVfBgQOOhqF8jCZ3pQrJMTkM+d5OwDGk7RDKRpR1NJ6XXoKFC2H0aEfDUD5Gk7tShcxYPYOV+1dSNaYqD13xkNPhMG6cnbXpjTdg06biyysFmtyVOkVqZipPL7Bz343sMJLIUOcbvhs2hPvuszc05U3Lp1RxNLkrVcDLv77MzsSdNK7YmF5NezkdzkmjRtkfWD/7DJYscToa5Qs0uSuVa2/SXsb+NBaAl69/meAg7xm16+KL4bHH7PoTT4AxzsajvJ8md6VyPbPgGVIyU+hcpzNX17za6XBO8+STEBcHGzbYMd+VOhu9iUkp4H97/8e7f7xLaFAoL3Z60elwihQTY8d5r1cPypVzOhrl7TS5q4BnjOGxbx/DYHj4iodLdJiBc9WmjdMRKF+hzTIq4H22/jMW7lhI+cjyDOswzOlwXJKWZrtIavOMOhNN7iqgJaUn8eg3jwIw5uoxjt+w5KqhQ2HIEHj8cacjUd5Kk7sKaKMWjmJ30m4SqiTQp3kfp8Nx2eOPQ1QUzJ4N8+Y5HY3yRprcVcBavX81r/z6CoIw+abJXtX1sThVqsCw3Bakhx6yzTRKFaTJXQWkHJNDvy/7kW2y6Z/QnxZVWjgd0jkbOND2nPnzTxg71ulolLfR5K4C0vsr3+fnv37moqiLGHP1GKfDOS9hYfDmm3Z93DhYt87ZeJR30eSuAs7BlIMM+m4QABOum+AzP6IWpW1b6NsXMjNh6lSno1HeRPu5q4Dzr2/+xaETh+hYoyM9GvVwOpwLNm4cdOhgp+ZTKo8mdxVQZm+YzUdrPqJUaCne7vw2IuJ0SBcsNha6d3c6CuVttFlGBYyjqUfp92U/AJ6/5nlqxdZyOCL327TJDgusA4sprbmrgPHYvMfYl7yPNtXaeMUkHO6Wnm6n49u7F2rXtmPAq8ClNXcVEL7c9CVT/5hKeHA4UzpPIUj8708/PBzGj7frjzwCO3Y4G49ylv/9hStVyP7k/dw/937ADjFQp0IdhyPynLvvhltvhaQkuP9+yMlxOiLlFJeSu4iUE5FZIpIiIjtEpMifb0TkXhFZISLHRWSXiLwgItr0oxxjjOH+ufdzIOUAV9e8msdaPeZ0SB4lYudarVABFiyAiROdjkg5xdWa+0QgA6gI9AAmi0iDIsqVAh4FKgBXAtcAT1x4mEqdn0nLJvHVn18RGxHLe7e+55fNMYVddJFN8GBnbfrjD0fDUQ4p9i9dRKKArsAwY0yyMWYxMBfoWbisMWayMeYnY0yGMWY38AGgI1ArR6w9sJYnvrN1i7dueYuqMVUdjqjk3HabvblJxM7cpAKPK9WYy4FsY8ymAttWAkXV3AtrD6wtaoeI9BWR5SKy/ODBgy68lVKuS8lI4R+f/oO0rDTub3o/Xet3dTqkEvfKK7B8Odx5p9ORKCe4ktyjgcRC2xKB0md7kYjcB8QDRc5ZZox50xgTb4yJj4uLcyVWpVxijKHP531Ye3AtdSvU5dUbXnU6JEdERkLDhvnPU1Odi0WVPFeSezIQU2hbDJB0pheIyK3AOOAGY8yh845OqfMwadkkZqyZQVRoFDPvmEl0WLTTITlu+nSoWRNWrnQ6ElVSXEnum4AQESk4sWQTztzc8jfgLeAWY8zqCw9RKdf9uutXBn47EIApnadQL66ewxF5h/nzYf9+6NIFDml1KyAUm9yNMSnATGC0iESJSBugCzCtcFkRuRr7I2pXY8xv7g5WqbPZm7SXbp90IzMnk0eufIR/NPyH0yF5jddfh4QEe2PTHXfYUSSVf3O1X1h/IBI4AMwA+hlj1opIdRFJFpHqueWGAWWAr3K3J4vI1+4PW6lTncg8QZePurDr+C7aVGvDC51ecDokrxIRATNnQsWK8MMPtouk8m8u3WBkjDkC3FrE9p3YH1zznnd0W2RKuSjH5HDv7HtZtmcZNcvWZNY/ZhEWHOZ0WF6nalWb4K+6Cv7zH6hfHx580OmolKf4/x0dyu8N/2E4n677lJjwGL7o/gVxUdr76kxat4bJk+364MFw5Iiz8SjP0aEBlE+bvGwyz/30HMESzMe3f0z9uPpOh+T1eveGY8fg6quhXDmno1Geosld+awZq2cw4KsBAEy+aTLXX3a9wxH5jscfP/V5Roadk1X5D22WUT7p6z+/5p7Z92AwPH/N8/Rp0cfpkHzWtGm2/X3bNqcjUe6kyV35nAXbFtD1465k5WTxRKsneKrNU06H5LOysuwgY1u22GaanTudjki5iyZ35VO+2/IdN314E6lZqTzQ7AFe6PSCX8yD6pSQEPjqK7jySti+HTp2hF27nI5KuYMmd+Uzvt38LbfMuIW0rDT6NO/DG7e8oYndDWJi4JtvID4etm61CX77dqejUhdKk7vyCZ+u+5QuH3UhPTudfvH9eP3m1wNibPaSUrYszJsHzZvD5s22y+RqHTzEp+n/DuX1Xlv6Gnd8cgfp2en864p/MfHGiZrYPSA21s7e1KGDHUFSvxT5Nu0KqbxWjsnh6e+fZvzPdtbnsVePZXDbwdoU40Flytgmmj//PHW4YOV7NLkrr3Q8/Tj3zLqHORvnECzBTOk8hXub3ut0WAEhIgIaNcp//n//B4cPw7BhEKRfmHyGJnfldf48/CddPurC+kPrKRtRlo+6fqQ3KDlk1y57w1NGBqxZA1OnQlSU01EpV+jnsPIqczfOJeGtBNYfWk/9uPr89sBvmtgdVLUqzJple9R8+im0bAlri5zJQXkbTe7KK6RmpjLgywF0+agLiemJ3Fr3Vn7t/Su1y9cu/sXKo268EZYuhTp1bO09IQHeeguMcToydTaa3JXjVu1fRcJbCUxaPonQoFAmXDeBz+74jNLhZ52mV5WgunXtZNu9etmeNH37wvjxTkelzkaTu3JMelY6w38YTvyb8aw9uJY65euw9IGlPNbqMe3q6IWio+Hdd+18rFWqQPfuTkekzkb/BylHLN65mKZvNOXZRc+SmZPJP1v8kxV9V9CscjOnQ1PF6NHDjkVTPXf+tZwcGDpUx6XxNprcVYnambiTHjN70O7ddmw4tIG6FeqyqNciJt88magw7YbhKyIi8tdffx3GjrVt8sOHQ0qKc3GpfJrcVYlISk9i6PdDqfN/dfhw9YeEB4czvP1w/njwD9pd0s7p8NQF6NIF7roL0tLg2Wdtkn//fcjOdjqywKbJXXlUUnoS4xaPo9Z/ajF28VjSstK4s+GdbHhoA6M6jiI8JNzpENUFuvhi+PBDWLwYWrSA3bvh3nvtHa6ff+50dIFLb2JSHnEk9QgTf5vIy7++zNG0owC0rtaaFzu9SKtqrRyOTnlCmzbw22928o+RI2HDBpvolTM0uSu3WrV/Fa8tfY0PVn9AalYqAG2rt2VEhxFcU/MaHRfGzwUF2Vp79+4wYwbceWf+vuees5OD/POfULGiczEGCjFecCdCfHy8Wb58udNhqPOUnJHMrPWzePv3t1m0Y9HJ7dddeh1D2g6hwyUdNKkHuKQke7fr8eN2rtauXe2HwLXXQnCw09H5LhFZYYyJL2qf1tzVecnOyeb7bd8zbdU0Zq6fyYnMEwBEh0XTq0kvHrriIepUqONwlMpbREfD7Nnw6qswd66t1c+YYdvr774bHn7Yriv30Zq7cllyRjLztsxj7sa5fLHpCw6nHj65r3W11vRs3JPujboTEx7jYJTK2+3YYXvTvPee7S8PdmKQvCGG9+61zTY6AmXxzlZz1+SuzijH5LBy30p+2P4D87fOZ8G2BaRnp5/cX7tcbXo06sHdje/m0nKXOhip8kXGwM8/2zlcn3suf3KQK66Abdvgmmtss82110KNGo6G6rU0uSuXpGam8vu+3/lt92/8uP1HFu1YdLKnC4AgtKzaks51OtO5TmfqVainbenKrZKToXFjm9wLuvRSaNvW/hjbsqUzsXkjbXNXpzmWdox1B9exev9qlu9ZzrI9y1hzYA3Z5tQ7T2qUrUHHGh25qsZVXH/p9VSM1m4OynOio21TzaZNMH++XRYssNu2bIHOnfPLzp4NixbZD4PGjaF+/VPvnA10mtz9WFpWGjuO7WD7se1sPbqVDYc2sO7QOtYeWMve5L2nlQ+SIBpXbEx85XjaVm9Lx5odqVG2RskHrgKaiL3LtU4dGDDAdp/8/XdYsgTaFbiZee5cO5BZnuBgqF3bJvlWreCJJ/L3GRN4c8JqcvdRSelJ7Eved3LZm7yXfcn7+Ov4X2w7uo1tx7axJ2nPGV8fGRJJvbh6NIhrQPPKzUmokkCzys0oFVqqBM9CqeKFhNgx5BMSTt1+3322uWbVKrts2mRvnNqwwTbv5CX3pCT7A+0ll9geOVWr2iVvvVUrqFCh5M/L01xK7iJSDpgCXAccAoYYYz48Q9mBwFNAJPAZ0M8Yk15U2UBljCEjO4OUzBRSMlJIyUwhOSOZpPQkjqYd5Wjq0VMej6QeOfn8cOph9ifvJyWz+NGZgiWYamWqUbNsTWqWrUmdCnWoH1ef+nH1qVG2hg6rq3xau3an1uRTU2H9eti4EcqWzd++bZvdl5f4C/v2W7juOrs+Zoz9NhAXZxN+3hIbC9WqwT335L/u99/tlIMxMXaJjPSubweu1twnAhlARaAp8KWIrDTGnDLhlohcDwwGrgb2ALOAUbnb3C45I5mUjBSyTTbZOdnkmJyT69km93nu+rlsK/g+WTlZZGRnkJGdQXp2ev56VnrR2wuVOZF54rQknhfzhYgIiaBydGUqRVeicunKVIqqRKXoSlwcc7FN5rE1qRpTlZAg/XKmAkNkJDRvbpeCGjeGxEQ7JPHu3XZe2F278tdr1covu3MnbN1ql8IaN85P7sbYXj1ZWfn7g4NtDJGR8O9/25u0AL78EiZMyN+Xt0RE2GM/+qhb/xlOKvZ/vohEAV2BhsaYZGCxiMwFenJ60r4XmJKX9EXkWeCDIsq5xaB5g3h9xeueeGuPCw0KJSosiqjQKKLCoogOiyY6LJrYiFhiI2PtY8H1yFjKRZYjNiKWStGViAmP0Z4qSrkoJsb2o8/rS38mL75om3MOHcpfDh6EY8dObbrJzIQmTeyHxvHjdklLs81BycmnJv0dO+CHH4o+3pVXOpjcgcuBbGPMpgLbVgIdiijbAJhTqFxFESlvjDlcsKCI9AX6AlTPG/X/HJWJKENcqTiCg4IJlmCCJOjk+rlsC5KgU/YX3BYSFEJ4SDhhQWGEBYfZ9eDc9eDwM27LW0qFljqZvPMSeVRoFKHBoed1zkopz8lrYrn88rOXCwuz0w4WlJVlm39SU21zTZ4uXeyPw3n7Ci4XXeT+c8hTbD93EWkHfGKMqVRgWx+ghzHmqkJltwADjDHf5D4PxTbn1DTGbD/TMbSfu1JKnbuz9XN35Re1ZKDw/eQxQJILZfPWiyqrlFLKQ1xJ7puAEBGpXWBbE2BtEWXX5u4rWG5/4SYZpZRSnlVscjfGpAAzgdEiEiUibYAuwLQiir8P9BaR+iISCzwDTHVjvEoppVzgakfn/th+6weAGdi+62tFpLqIJItIdYDctvYXgB+AHbnLCPeHrZRS6mxc6gRtjDkC3FrE9p1AdKFtLwEvuSM4pZRS50dvUVRKKT+kyV0ppfyQJnellPJDXjFZh4gcxP74ej4qYAcz8wd6Lt7JX87FX84D9FzyXGKMiStqh1ck9wshIsvPdIeWr9Fz8U7+ci7+ch6g5+IKbZZRSik/pMldKaX8kD8k9zedDsCN9Fy8k7+ci7+cB+i5FMvn29yVUkqdzh9q7koppQrR5K6UUn5Ik7tSSvkhn0juIlJORGaJSIqI7BCR7mcpO1BE9olIooi8IyLhJRnr2bh6HiLSS0Syc0fczFuuKtloz05EHhKR5SKSLiJTiynrzdfEpfPwkWsSLiJTcv+2kkTkdxG54SzlvfK6nMt5+Mh1mS4ie0XkuIhsEpEHzlLWbdfEJ5I7MBE7XV9FoAcwWUQaFC4kItdjJ+O+BqgB1AJGlVyYxXLpPHItMcZEF1h+LKkgXbQHGAO8c7ZCPnBNXDqPXN5+TUKAv7DzG5cBhgEfi0iNwgW9/Lq4fB65vP26PA/UMMbEAJ2BMSLSonAhd18Tr0/uIhIFdAWGGWOSjTGLgblAzyKK3wtMMcasNcYcBZ4FepVYsGdxjufh9YwxM40xs4HiZtny2msC53QeXs8Yk2KMGWmM2W6MyTHGfAFsA05LJHjxdTnH8/B6uf/G6XlPc5dLiyjq1mvi9ckduBzINsZsKrBtJVBUjbdB7r6C5SqKSHkPxueqczkPgGYicij3a9wwEXFp7H0v5M3X5Fz51DURkYrYv7uipsT0metSzHmAD1wXEZkkIieADcBe4Ksiirn1mvhCco8GEgttSwRKu1A2b72osiXtXM5jEdAQuAhb278LGOTR6DzHm6/JufCpayIiocAHwHvGmA1FFPGJ6+LCefjEdTHG9Mf+27bDTluaXkQxt14TX0juyUBMoW0xQJILZfPWiypb0lw+D2PMVmPMttyvpKuB0cDtJRCjJ3jzNXGZL10TEQnCznGcATx0hmJef11cOQ9fui7GmOzc5tiqQL8iirj1mvhCct8EhIhI7QLbmlD0V7S1ufsKlttvjPGG9tRzOY/CDCAeicrzvPmaXAivvCYiIsAU7I/2XY0xmWco6tXX5RzOozCvvC6FhFB0m7tbr4nXJ3djTAr2a8xoEYkSkTZAF+wnemHvA71FpL6IxALPAFNLLNizOJfzEJEbctsZEZG62N4Cc0oy3uKISIiIRADBQLCIRJyhrdNrrwm4fh6+cE1yTQbqAbcYY1LPUs6rrwsunoe3XxcRuUhE7hSRaBEJzu0RcxewoIji7r0mxhivX4BywGwgBdgJdM/dXh37VaZ6gbKPAfuB48C7QLjT8Z/reQAv5p5DCrAV+1Uz1On4C53LSPJ/+c9bRvrgNXHpPHzkmlySG39abux5Sw9fui7nch7efl2AOGAhcCz333k10Cd3n0eviQ4cppRSfsjrm2WUUkqdO03uSinlhzS5K6WUH9LkrpRSfkiTu1JK+SFN7kop5Yc0uSullB/S5K6UUn7o/wHMUy2QU38n9wAAAABJRU5ErkJggg==)]

Softmax回归

类k的Softmax分数
$$s_k(x)=x^T{\Theta }^{(k)}$$
Softmax函数
$$\begin{gathered} {\hat{p}}_k=\sigma (s(x){)}_k=\frac{exp(s_k(x))}{{\sum }_{j=1}^{k}exp(s_j(x))} \\ 此等式中 \\ K是类数 \\ s(x)是一个向量，其中包括实例x的每个类的分数 \\ \sigma (s(x){)}_k是实例x属于类k的估计概率，给定该实例每个类的分数 \end{gathered}$$
Softmax回归分类预测
$$\hat{y}=argmax\sigma (s(x){)}_k=argmax{s}_k(x)=argmax(({\Theta }^k{)}^{T}x)$$
交叉熵成本函数
$$\begin{gathered} J(\Theta )=-\frac{1}{m}\sum _{i=1}^m\sum _{k=1}^k{y}_k^{(i)}log({\hat{p}}_l^{(i)}) \\ 在此等式中y_k^{(i)}是属于类k的第i个实例的目标概率。一般而言等于1或0，具体取决于实例是否属于该 \end{gathered}$$

介绍

交叉熵（Cross Entropy）是Shannon信息论中一个重要概念，主要用于度量两个概率分布间的差异性信息。语言模型的性能通常用交叉熵和复杂度（perplexity）来衡量。交叉熵的意义是用该模型对文本识别的难度，或者从压缩的角度来看，每个词平均要用几个位来编码。复杂度的意义是用该模型表示这一文本平均的分支数，其倒数可视为每个词的平均概率。平滑是指对没观察到的N元组合赋予一个概率值，以保证词序列总能通过语言模型得到一个概率值。通常使用的平滑技术有图灵估计、删除插值平滑、Katz平滑和Kneser-Ney平滑。

公式

将交叉熵引入计算语言学消岐领域，采用语句的真实语义作为交叉熵的训练集的先验信息，将机器翻译的语义作为测试集后验信息。计算两者的交叉熵，并以交叉熵指导对歧义的辨识和消除。实例表明，该方法简洁有效．易于计算机自适应实现。交叉熵不失为计算语言学消岐的一种较为有效的工具。

在信息论中，交叉熵是表示两个概率分布p,q，其中p表示真实分布，q表示非真实分布，在相同的一组事件中，其中，用非真实分布q来表示某个事件发生所需要的平均比特数。从这个定义中，我们很难理解交叉熵的定义。下面举个例子来描述一下：

假设现在有一个样本集中两个概率分布p,q，其中p为真实分布，q为非真实分布。假如，按照真实分布p来衡量识别一个样本所需要的编码长度的期望为：

H§=

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DYioVdqB-1658889211625)(https://bkimg.cdn.bcebos.com/formula/d8600ed8a168b3ccde14700c4edba145.svg)]

但是，如果采用错误的分布q来表示来自真实分布p的平均编码长度，则应该是：

H(p,q)=

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lk1m7IsR-1658889211626)(https://bkimg.cdn.bcebos.com/formula/4f4bd894f88b051dbcb362809a886c10.svg)]

此时就将H(p,q)称之为交叉熵。交叉熵的计算方式如下：

对于离散变量采用以下的方式计算：H(p,q)=

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CyFkN1Yr-1658889211626)(https://bkimg.cdn.bcebos.com/formula/39dffa5dea6b891ae6a322110c04ea1a.svg)]

对于连续变量采用以下的方式计算：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l9Gu7e8Y-1658889211626)(https://bkimg.cdn.bcebos.com/formula/86749cf53f17a226a4e45c56664cae10.svg)]

类k的交叉熵梯度向量
$${\nabla }_{\Theta (k)}J(\Theta )=\frac{1}{m}\sum _{i=1}^m({\hat{p}}_k^{(i)}-y_k^{(i)})x^{(i)}$$

'''Softmax回归'''
iris = datasets.load_iris()
X= iris["data"][:, (2, 3)]  # petal length, petal width
y = iris["target"]

softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(X, y)
x0, x1 = np.meshgrid(
        np.linspace(0, 8, 500).reshape(-1, 1),
        np.linspace(0, 3.5, 200).reshape(-1, 1),
    )
X_new = np.c_[x0.ravel(), x1.ravel()]


y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)

zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
#画图
plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")

from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])

plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

代码总结

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression,SGDRegressor,LogisticRegression
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.base import clone
from sklearn.pipeline import Pipeline
from copy import  deepcopy
from sklearn import datasets


x = 2*np.random.rand(100,1)
y = 4+3*x+np.random.randn(100,1)

x_b = np.c_[np.ones((100,1)),x]
theta_best = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y)

x_new = np.array([[0],[2]])
x_new_b = np.c_[np.ones((2,1)),x_new]
y_predict = x_new_b.dot(theta_best)

#使用sklearn
lin_reg = LinearRegression()
lin_reg.fit(x,y)

'''批量梯度下降'''
eta = 0.1
n_iteration = 1000#迭代次数
m = 100

theta = np.random.randn(2,1)
for n in range(n_iteration):
    gradienters = 2/m*x_b.T.dot(x_b.dot(theta)-y)#偏导计算
    theta = theta-eta*gradienters #更改theta

'''随机梯度下降'''
n_epochs = 50#向前或向后迭代次数

t0,t1 = 5,50 #学习步长超参数

def learning_schedule(t):#计算步长
    return t0/(t+t1)#步长逐渐减小

theta = np.random.randn(2,1)
for n in range(n_epochs):
    for i in range(m):
        random_index = np.random.randint(m)
        xi = x_b[random_index:random_index+1]
        yi = y[random_index:random_index+1]
        gradienters = 2*xi.T.dot(xi.dot(theta)-yi)
        eta = learning_schedule(n*m+i)
        theta = theta-eta*gradienters


sgd_reg = SGDRegressor(max_iter=1000,tol = 1e-3,penalty=None,eta0=0.1)
sgd_reg.fit(x,y.ravel())
print(sgd_reg.intercept_,sgd_reg.coef_)

'''小批量梯度下降'''
theta_path_mgd = []

n_iterations = 50
minibatch_size = 20

np.random.seed(42)
theta = np.random.randn(2,1)  # random initialization

t0, t1 = 200, 1000
def learning_schedule(t):
    return t0 / (t + t1)

t = 0
for epoch in range(n_iterations):
    shuffled_indices = np.random.permutation(m)
    x_b_shuffled = x_b[shuffled_indices]
    y_shuffled = y[shuffled_indices]
    for i in range(0, m, minibatch_size):
        t += 1
        xi = x_b_shuffled[i:i+minibatch_size]
        yi = y_shuffled[i:i+minibatch_size]
        gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
        eta = learning_schedule(t)
        theta = theta - eta * gradients
        theta_path_mgd.append(theta)

'''多项式回归'''
m = 100
x = 6*np.random.rand(m,1)-3
y = 0.5*x**2+x+2+np.random.randn(m,1)

poly_features = PolynomialFeatures(degree=2,include_bias=False)#聚类特征
x_poly = poly_features.fit_transform(x)

lin_reg = LinearRegression()
lin_reg.fit(x_poly,y)
画图
X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(x, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([-3, 3, 0, 10])

plt.show()

'''学习曲线'''
def plot_learning_curves(model,x,y):
    x_train,x_val,y_train,y_val = train_test_split(x,y,test_size=0.2)
    train_erros,val_erros = [],[]
    for m in range(1,len(x_train)):
        model.fit(x_train[:m],y_train[:m])
        y_train_pred = model.predict(x_train[:m])
        y_val_pred = model.predict(x_val)
        train_erros.append(mean_squared_error(y_train[:m],y_train_pred))
        val_erros.append(mean_squared_error(y_val,y_val_pred))
    plt.plot(np.sqrt(train_erros),'r-+',linewidth = 2,label = 'train')
    plt.plot(np.sqrt(val_erros),'b--',linewidth = 3,label = 'val')
    plt.show()


lin_reg = LinearRegression()
plot_learning_curves(lin_reg,x,y)

'''岭回归'''
np.random.seed(42)
m = 20
X = 3 * np.random.rand(m, 1)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5
X_new = np.linspace(0, 3, 100).reshape(100, 1)

ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
ridge_reg = Ridge(alpha=1, solver="sag", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
'''lasso'''
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])

'''提前停止'''
np.random.seed(42)
m = 100
x = 6 * np.random.rand(m, 1) - 3
y = 2 + x + 0.5 * x**2 + np.random.randn(m, 1)

x_train, x_val, y_train, y_val = train_test_split(x[:50], y[:50].ravel(), test_size=0.5, random_state=10)
poly_scaler = Pipeline([('poly_features',PolynomialFeatures(degree=90,include_bias=False)),('std_scaler',StandardScaler())])
x_train_poly_scaled = poly_scaler.fit_transform(x_train)
x_val_poly_scaled = poly_scaler.transform(x_val)
sgd_reg = SGDRegressor(max_iter=1,tol=-np.infty,warm_start=True,penalty=None,learning_rate='constant',eta0=0.0005)
minimum_val_error = float('inf')
best_epoch = None
best_model = None
for epoch in range(1000):
    sgd_reg.fit(x_train_poly_scaled,y_train)
    y_val_predict = sgd_reg.predict(x_val_poly_scaled)
    val_error = mean_squared_error(y_val, y_val_predict)
    if val_error < minimum_val_error:
        minimum_val_error = val_error
        best_epoch = epoch
        best_model = deepcopy(sgd_reg)

#画图
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
                       penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)

n_epochs = 500
train_errors, val_errors = [], []
for epoch in range(n_epochs):
    sgd_reg.fit(x_train_poly_scaled, y_train)
    y_train_predict = sgd_reg.predict(x_train_poly_scaled)
    y_val_predict = sgd_reg.predict(x_val_poly_scaled)
    train_errors.append(mean_squared_error(y_train, y_train_predict))
    val_errors.append(mean_squared_error(y_val, y_val_predict))

best_epoch = np.argmin(val_errors)
best_val_rmse = np.sqrt(val_errors[best_epoch])

plt.annotate('Best model',
             xy=(best_epoch, best_val_rmse),
             xytext=(best_epoch, best_val_rmse + 1),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.05),
             fontsize=16,
            )

best_val_rmse -= 0.03  # just to make the graph look better
plt.plot([0, n_epochs], [best_val_rmse, best_val_rmse], "k:", linewidth=2)
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="Validation set")
plt.plot(np.sqrt(train_errors), "r--", linewidth=2, label="Training set")
plt.legend(loc="upper right", fontsize=14)
plt.xlabel("Epoch", fontsize=14)
plt.ylabel("RMSE", fontsize=14)

plt.show()

'''决策边界'''
iris = datasets.load_iris()
x = iris['data'][:,3:]
y = (iris['target']==2).astype(np.int_)
log_reg = LogisticRegression()
log_reg.fit(x,y)
#画图展示模型估算出的概率
x_new = np.linspace(0,3,1000).reshape(-1,1)
y_proba = log_reg.predict_proba(x_new)
plt.plot(x_new,y_proba[:,1],'g-',label = 'Iris virginica')
plt.plot(x_new,y_proba[:,0],'b--',label = 'Not Iris virginica')
plt.show()
'''Softmax回归'''
iris = datasets.load_iris()
X= iris["data"][:, (2, 3)]  # petal length, petal width
y = iris["target"]

softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(X, y)
x0, x1 = np.meshgrid(
        np.linspace(0, 8, 500).reshape(-1, 1),
        np.linspace(0, 3.5, 200).reshape(-1, 1),
    )
X_new = np.c_[x0.ravel(), x1.ravel()]


y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)

zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)

plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")

from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])

plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253

]

y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)

zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)

plt.figure(figsize=(10, 4))
plt.plot(X[y2, 0], X[y2, 1], “g^”, label=“Iris virginica”)
plt.plot(X[y1, 0], X[y1, 1], “bs”, label=“Iris versicolor”)
plt.plot(X[y0, 0], X[y0, 1], “yo”, label=“Iris setosa”)

from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap([‘#fafab0’,‘#9898ff’,‘#a0faa0’])

plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel(“Petal length”, fontsize=14)
plt.ylabel(“Petal width”, fontsize=14)
plt.legend(loc=“center left”, fontsize=14)
plt.axis([0, 7, 0, 3.5])

plt.show()

1