【二】MATLAB矩阵处理_创建一个5阶魔方矩阵a,求a的行列式值、a的转置矩阵、a的逆矩阵和a的秩,提取矩阵a

【二】MATLAB矩阵处理

1 常用的特殊矩阵函数

zeros函数：

zeros(m):产生m×m零矩阵

zeros(m,n):产生m×n零矩阵

zeros(size(A)):产生与矩阵A相同大小的零矩阵

ones函数：

产生4阶全1矩阵

ones(4)

eye函数：

产生对角线为1的矩阵，当矩阵是方阵时，得到一个单位矩阵

eg:产生5阶对角线为1的矩阵

eye(5)

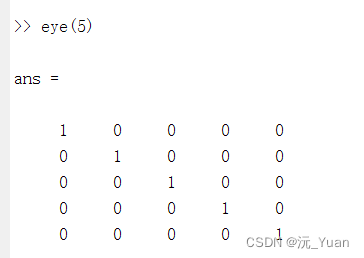
rand函数：产生(0,1)区间均匀分布的随机矩阵

eg:

产生5阶随机矩阵

rand(5)

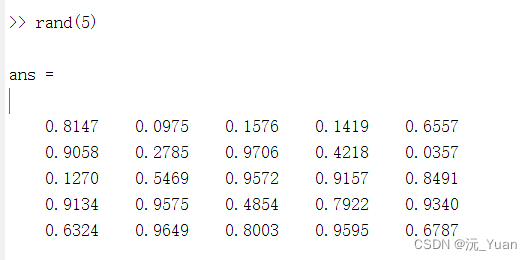
产生1×5阶随机矩阵

rand(1,5)

randn函数：产生均值为0，方差为1的标准正态分布随机矩阵

用法与rand类似

eg:

产生5阶正态分布随机矩阵

randn(5)

产生1×5阶正态分布随机矩阵

randn(1,5)

magic函数：产生魔方矩阵(每行每列相加值都一样)

eg:

产生3阶魔方矩阵

M=magic(3)

vander函数：产生范德蒙矩阵

eg:

v=1:5

A=vander(v)

hilb函数：生成希尔伯特矩阵

eg:

产生5阶希尔伯特矩阵

hilb(5)

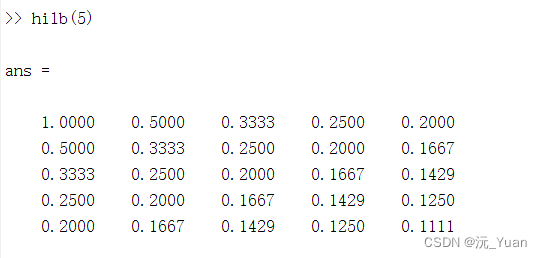
compan函数：生成伴随矩阵

eg:

p=[1,2,3,4]

A=compan§

pascal函数：帕斯卡矩阵（与杨辉三角形有关）

eg：

产生5阶帕斯卡矩阵

pascal(5)

2 矩阵求值

det函数:求行列式值

eg:

求方阵A对应的行列式的值

det(A)

rank函数：求矩阵的秩

eg:

求矩阵A的秩

rank(A)

trace函数：求矩阵的迹

eg:

求矩阵A的秩

b=trace(A)

另外一种求法：

t=sum(diag(A))

范数

矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度

向量1范数：向量元素绝对值之和

norm(v,1)

计算向量v的1范数

向量2范数：向量元素绝对值的平方和的平方根

norm(v,2)

计算向量v的2范数

向量无穷范数：所有向量元素绝对值中的最大值

norm(v,inf)

计算向量v的无穷范数

条件数

矩阵A的条件数等于A的范数与A的逆矩阵的范数的乘积

条件数越接近于1，矩阵的性能越好，反之，矩阵的性能越差

cond(A,1)

A的1范数下的条件数

cond(A,2)

A的2范数下的条件数

cond(A,inf)

A的无穷范数下的条件数

3 矩阵的特征值与特征向量

eig函数:计算函数特征值和特征向量

E=eig(A)

求矩阵A的全部特征值组成向量E

[X,D]=eig(A)

求矩阵A的全部特征值，构成对角阵D，并产生矩阵X，X各列是相应的特征向量

4 稀疏矩阵

完全存储方式:将矩阵的全部元素按列存储

稀疏存储方式:只存储矩阵的非零元素的值及其位置，即行号和列号

由稀疏存储方式存储的矩阵就叫做稀疏矩阵

A=sparee(S)

将矩阵S转化为稀疏矩阵

S=full(A)

将矩阵A转化为完全矩阵

sparse函数调用

sparse(m,n)

生成m×n所有元素都是0的稀疏矩阵

sparse(u,v,S)

其中u、v、s是3个等长的向量。S是要建立的稀疏存储矩阵的非零元素，u(i)、v(i)分别是S(i)的行和列

下标。

speye函数

speye(m,n)

返回一个m×n的稀疏矩阵

课程链接：https://www.icourse163.org/course/CSU-1002475002#/info

sparse(m,n)

生成m×n所有元素都是0的稀疏矩阵

sparse(u,v,S)

其中u、v、s是3个等长的向量。S是要建立的稀疏存储矩阵的非零元素，u(i)、v(i)分别是S(i)的行和列

下标。

speye函数

speye(m,n)

返回一个m×n的稀疏矩阵

课程链接：https://www.icourse163.org/course/CSU-1002475002#/info