- 1Androidstudio ADB调试_andriod studio canary11 adb 调试
- 2通过mac电脑将macos系统的dmg镜像转换为iso文件,供VMware安装mac系统_dmg转iso
- 3自动驾驶合集5
- 4【免费】如何考取HarmonyOS应用开发者基础认证和高级认证(详细教程)_华为开发者认证考试在哪里打开
- 5CodeWhisperer--手把手教你使用一个十分强大的工具_coderormer
- 6Android性能优化系列之Bitmap图片优化_android 列表获取封面 bitmapfactory.decodebytearray 太卡
- 7使用 python nltk 库对预料库进行自动词性标注_怎么利用nltk进行词性标注要把语料放哪里
- 8BERT_论文解析_bert 论文
- 9VUE点击切换样式_vue ul li 文本内容样式
- 10pycharm中的terminal运行前面的PS如何修改成自己环境_terminal里面ps怎么换成base
图神经网络的介绍
赞
踩
近年来,深度学习领域关于图神经网络(Graph Neural Networks,GNN)的研究热情日益高涨,图神经网络已经成为各大深度学习顶会的研究热点。GNN处理非结构化数据时的出色能力使其在网络数据分析、推荐系统、物理建模、自然语言处理和图上的组合优化问题方面都取得了新的突破。
图神经网络有很多比较好的综述[1][2][3]可以参考,更多的论文可以参考清华大学整理的GNN paper list[4] 。
本篇文章将从一个更直观的角度对当前经典流行的GNN网络,包括GCN、GraphSAGE、GAT、GAE以及graph pooling策略DiffPool等等做一个简单的小结。
一、为什么需要图神经网络?
随着机器学习、深度学习的发展,语音、图像、自然语言处理逐渐取得了很大的突破,语音、图像、文本都是很简单的序列或者网格数据,是很结构化的数据,深度学习很善于处理该种类型的数据(图1)。

图1
然而现实世界中并不是所有的事物都可以表示成一个序列或者一个网格,例如社交网络、知识图谱、复杂的文件系统等(图2),也就是说很多事物都是非结构化的。

图2
相比于简单的文本和图像,这种网络类型的非结构化的数据非常复杂,处理它的难点包括:
- 图的大小是任意的,图的拓扑结构复杂,没有像图像一样的空间局部性
- 图没有固定的节点顺序,或者说没有一个参考节点
- 图经常是动态图,而且包含多模态的特征
那么对于这类数据我们该如何建模呢?能否将深度学习进行扩展使得能够建模该类数据呢?这些问题促使了图神经网络的出现与发展。
二. 图神经网络是什么样子的?
相比较于神经网络最基本的网络结构全连接层(MLP),特征矩阵乘以权重矩阵,图神经网络多了一个邻接矩阵。计算形式很简单,三个矩阵相乘再加上一个非线性变换(图3)。

图3
因此一个比较常见的图神经网络的应用模式如下图(图4),输入是一个图,经过多层图卷积等各种操作以及激活函数,最终得到各个节点的表示,以便于进行节点分类、链接预测、图与子图的生成等等任务。

图4
上面是一个对图神经网络比较简单直观的感受与理解,实际其背后的原理逻辑还是比较复杂的,这个后面再慢慢细说,接下来将以几个经典的GNN models为线来介绍图神经网络的发展历程。
三、图神经网络的几个经典模型与发展
1 . Graph Convolution Networks(GCN)[5]
GCN可谓是图神经网络的“开山之作”,它首次将图像处理中的卷积操作简单的用到图结构数据处理中来,并且给出了具体的推导,这里面涉及到复杂的谱图理论,具体推到可以参考[6][7]。推导过程还是比较复杂的,然而最后的结果却非常简单( 图5)。

我们来看一下这个式子,天呐,这不就是聚合邻居节点的特征然后做一个线性变换吗?没错,确实是这样,同时为了使得GCN能够捕捉到K-hop的邻居节点的信息,作者还堆叠多层GCN layers,如堆叠K层有:

上述式子还可以使用矩阵形式表示如下,
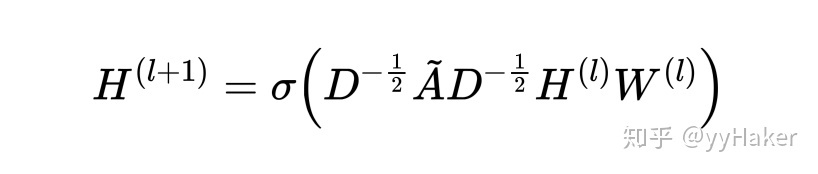
其中 ![[公式]](https://img-blog.csdnimg.cn/20210716160317240.png)
是归一化之后的邻接矩阵, ![[公式]](https://img-blog.csdnimg.cn/20210716160331659.png)
相当于给l层的所有节点的embedding做了一次线性变换,左乘以邻接矩阵表示对每个节点来说,该节点的特征表示为邻居节点特征相加之后的结果。(注意将 ![[公式]](https://img-blog.csdnimg.cn/20210716160409472.png)
换成矩阵 A 就是图3所说的三矩阵相乘)
那么GCN的效果如何呢?作者将GCN放到节点分类任务上,分别在Citeseer、Cora、Pubmed、NELL等数据集上进行实验,相比于传统方法提升还是很显著的,这很有可能是得益于GCN善于编码图的结构信息,能够学习到更好的节点表示。


图6
当然,其实GCN的缺点也是很显然易见的,第一,GCN需要将整个图放到内存和显存,这将非常耗内存和显存,处理不了大图;第二,GCN在训练时需要知道整个图的结构信息(包括待预测的节点), 这在现实某些任务中也不能实现(比如用今天训练的图模型预测明天的数据,那么明天的节点是拿不到的)。
2. Graph Sample and Aggregate(GraphSAGE)[8]
为了解决GCN的两个缺点问题,GraphSAGE被提了出来。在介绍GraphSAGE之前,先介绍一下Inductive learning和Transductive learning。注意到图数据和其他类型数据的不同,图数据中的每一个节点可以通过边的关系利用其他节点的信息。这就导致一个问题,GCN输入了整个图,训练节点收集邻居节点信息的时候,用到了测试和验证集的样本,我们把这个称为Transductive learning。然而,我们所处理的大多数的机器学习问题都是Inductive learning,因为我们刻意的将样本集分为训练/验证/测试,并且训练的时候只用训练样本。这样对图来说有个好处,可以处理图中新来的节点,可以利用已知节点的信息为未知节点生成embedding,GraphSAGE就是这么干的。
GraphSAGE是一个Inductive Learning框架,具体实现中,训练时它仅仅保留训练样本到训练样本的边,然后包含Sample和Aggregate两大步骤,Sample是指如何对邻居的个数进行采样,Aggregate是指拿到邻居节点的embedding之后如何汇聚这些embedding以更新自己的embedding信息。下图展示了GraphSAGE学习的一个过程,

K 第一步,对邻居采样
第二步,采样后的邻居embedding传到节点上来,并使用一个聚合函数聚合这些邻居信息以更新节点的embedding
第三步,根据更新后的embedding预测节点的标签
接下来,我们详细的说明一个训练好的GrpahSAGE是如何给一个新的节点生成embedding的(即一个前向传播的过程),如下算法图:

首先,(line1)算法首先初始化输入的图中所有节点的特征向量,(line3)对于每个节点 [公式] ,拿到它采样后的邻居节点 [公式] 后,(line4)利用聚合函数聚合邻居节点的信息,(line5)并结合自身embedding通过一个非线性变换更新自身的embedding表示。
注意到算法里面的 [公式] ,它是指聚合器的数量,也是指权重矩阵的数量,还是网络的层数,这是因为每一层网络中聚合器和权重矩阵是共享的。网络的层数可以理解为需要最大访问的邻居的跳数(hops),比如在图7中,红色节点的更新拿到了它一、二跳邻居的信息,那么网络层数就是2。为了更新红色节点,首先在第一层(k=1),我们会将蓝色节点的信息聚合到红色解节点上,将绿色节点的信息聚合到蓝色节点上。在第二层(k=2)红色节点的embedding被再次更新,不过这次用到的是更新后的蓝色节点embedding,这样就保证了红色节点更新后的embedding包括蓝色和绿色节点的信息,也就是两跳信息。
为了看的更清晰,我们将更新某个节点的过程展开来看,如图8分别为更新节点A和更新节点B的过程,可以看到更新不同的节点过程每一层网络中聚合器和权重矩阵都是共享的。

那么GraphSAGE Sample是怎么做的呢?GraphSAGE是采用定长抽样的方法,具体来说,定义需要的邻居个数 [公式] ,然后采用有放回的重采样/负采样方法达到 [公式] 。保证每个节点(采样后的)邻居个数一致,这样是为了把多个节点以及它们的邻居拼接成Tensor送到GPU中进行批训练。
那么GraphSAGE 有哪些聚合器呢?主要有三个,

这里说明的一点是Mean Aggregator和GCN的做法基本是一致的(GCN实际上是求和)。
到此为止,整个模型的架构就讲完了,那么GraphSAGE是如何学习聚合器的参数以及权重矩阵 [公式] 呢?如果是有监督的情况下,可以使用每个节点的预测lable和真实lable的交叉熵作为损失函数。如果是在无监督的情况下,可以假设相邻的节点的embedding表示尽可能相近,因此可以设计出如下的损失函数,

那么GrpahSAGE的实际实验效果如何呢?作者在Citation、Reddit、PPI数据集上分别给出了无监督和完全有监督的结果,相比于传统方法提升还是很明显。

至此,GraphSAGE介绍完毕。我们来总结一下,GraphSAGE的一些优点,
(1)利用采样机制,很好的解决了GCN必须要知道全部图的信息问题,克服了GCN训练时内存和显存的限制,即使对于未知的新节点,也能得到其表示
(2)聚合器和权重矩阵的参数对于所有的节点是共享的
(3)模型的参数的数量与图的节点个数无关,这使得GraphSAGE能够处理更大的图
(4)既能处理有监督任务也能处理无监督任务
(就喜欢这样解决了问题,方法又简洁,效果还好的idea!!!)
当然,GraphSAGE也有一些缺点,每个节点那么多邻居,GraphSAGE的采样没有考虑到不同邻居节点的重要性不同,而且聚合计算的时候邻居节点的重要性和当前节点也是不同的。
3. Graph Attention Networks(GAT)[9]
为了解决GNN聚合邻居节点的时候没有考虑到不同的邻居节点重要性不同的问题,GAT借鉴了Transformer的idea,引入masked self-attention机制,在计算图中的每个节点的表示的时候,会根据邻居节点特征的不同来为其分配不同的权值。
具体的,对于输入的图,一个graph attention layer如图9所示,

图9
其中 a 采用了单层的前馈神经网络实现,计算过程如下(注意权重矩阵 [公式] 对于所有的节点是共享的):
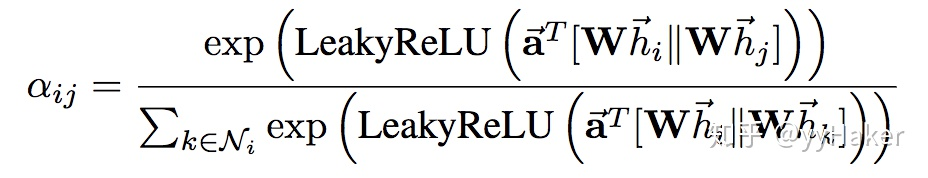
计算完attention之后,就可以得到某个节点聚合其邻居节点信息的新的表示,计算过程如下:
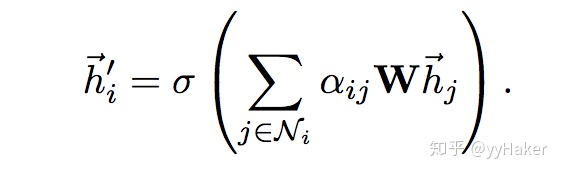
为了提高模型的拟合能力,还引入了多头的self-attention机制,即同时使用多个 [公式] 计算self-attention,然后将计算的结果合并(连接或者求和):

此外,由于GAT结构的特性,GAT无需使用预先构建好的图,因此GAT既适用于Transductive Learning,又适用于Inductive Learning。
那么GAT的具体效果如何呢?作者分别在三个Transductive Learning和一个Inductive Learning任务上进行实验,实验结果如下:

无论是在Transductive Learning还是在Inductive Learning的任务上,GAT的效果都要优于传统方法的结果。
至此,GAT的介绍完毕,我们来总结一下,GAT的一些优点,
(1)训练GCN无需了解整个图结构,只需知道每个节点的邻居节点即可
(2)计算速度快,可以在不同的节点上进行并行计算
(3)既可以用于Transductive Learning,又可以用于Inductive Learning,可以对未见过的图结构进行处理
(仍然是简单的idea,解决了问题,效果还好!!!)
到此,我们就介绍完了GNN中最经典的几个模型GCN、GraphSAGE、GAT,接下来我们将针对具体的任务类别来介绍一些流行的GNN模型与方法。
四、无监督的节点表示学习(Unsupervised Node Representation)
由于标注数据的成本非常高,如果能够利用无监督的方法很好的学习到节点的表示,将会有巨大的价值和意义,例如找到相同兴趣的社区、发现大规模的图中有趣的结构等等。

图10
Graph Auto-Encoder(GAE)[10]
在介绍Graph Auto-Encoder之前,需要先了解自编码器(Auto-Encoder)、变分自编码器(Variational Auto-Encoder),具体可以参考[11],这里就不赘述。
理解了自编码器之后,再来理解变分图的自编码器就容易多了。如图11输入图的邻接矩阵[公式]和节点的特征矩阵[公式],通过编码器(图卷积网络)学习节点低维向量表示的均值[公式]和方差[公式],然后用解码器(链路预测)生成图。
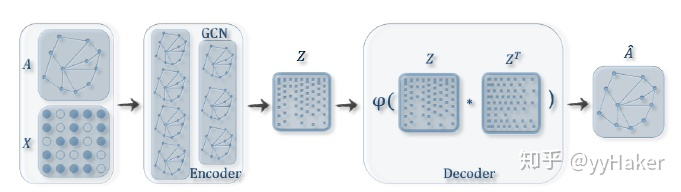
图11
编码器(Encoder)采用简单的两层GCN网络,解码器(Encoder)计算两点之间存在边的概率来重构图,损失函数包括生成图和原始图之间的距离度量,以及节点表示向量分布和正态分布的KL-散度两部分。具体公式如图12所示:

图12
另外为了做比较,作者还提出了图自编码器(Graph Auto-Encoder),相比于变分图的自编码器,图自编码器就简单多了,Encoder是两层GCN,Loss只包含Reconstruction Loss。
那么两种图自编码器的效果如何呢?作者分别在Cora、Citeseer、Pubmed数据集上做Link prediction任务,实验结果如下表,图自编码器(GAE)和变分图自编码器(VGAE)效果普遍优于传统方法,而且变分图自编码器的效果更好;当然,Pumed上GAE得到了最佳结果。可能是因为Pumed网络较大,在VGAE比GAE模型复杂,所以更难调参。

五、Graph Pooling
Graph pooling是GNN中很流行的一种操作,目的是为了获取一整个图的表示,主要用于处理图级别的分类任务,例如在有监督的图分类、文档分类等等。

图13
Graph pooling的方法有很多,如简单的max pooling和mean pooling,然而这两种pooling不高效而且忽视了节点的顺序信息;这里介绍一种方法:Differentiable Pooling (DiffPool)。
1.DiffPool[12]
在图级别的任务当中,当前的很多方法是将所有的节点嵌入进行全局池化,忽略了图中可能存在的任何层级结构,这对于图的分类任务来说尤其成问题,因为其目标是预测整个图的标签。针对这个问题,斯坦福大学团队提出了一个用于图分类的可微池化操作模块——DiffPool,可以生成图的层级表示,并且可以以端到端的方式被各种图神经网络整合。
DiffPool的核心思想是通过一个可微池化操作模块去分层的聚合图节点,具体的,这个可微池化操作模块基于GNN上一层生成的节点嵌入 [公式] 以及分配矩阵 [公式] ,以端到端的方式分配给下一层的簇,然后将这些簇输入到GNN下一层,进而实现用分层的方式堆叠多个GNN层的想法。(图14)

图14
那么这个节点嵌入和分配矩阵是怎么算的?计算完之后又是怎么分配给下一层的?这里就涉及到两部分内容,一个是分配矩阵的学习,一个是池化分配矩阵。
分配矩阵的学习
这里使用两个分开的GNN来生成分配矩阵S(l)和每一个簇节点新的嵌入Z(l),这两个GNN都是用簇节点特征矩阵 X(l) 和粗化邻接矩阵 A(l)作为输入,
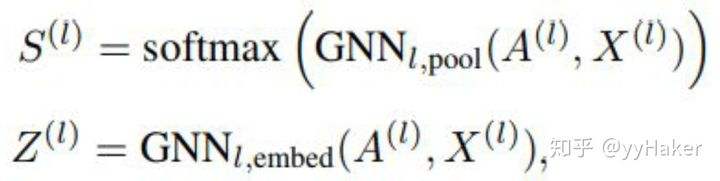
池化分配矩阵
计算得到分配矩阵S(l)和每一个簇节点新的嵌入Z(l)之后,DiffPool层根据分配矩阵,对于图中的每个节点/簇生成一个新的粗化的邻接矩阵 A(l-1)与新的嵌入矩阵X(l+1),
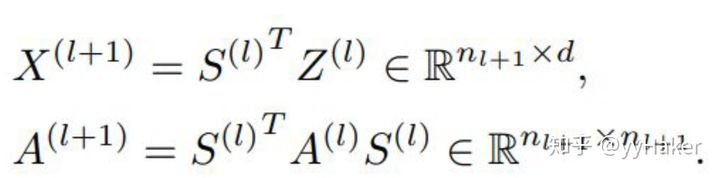
总的来看,每层的DiffPool其实就是更新每一个簇节点的嵌入和簇节点的特征矩阵,如下公式:
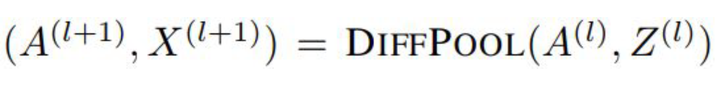
至此,DiffPool的基本思想就讲完了。那么效果如何呢?作者在多种图分类的基准数据集上进行实验,如蛋白质数据集(ENZYMES,PROTEINS,D&D),社交网络数据集(REDDIT-MULTI-12K),科研合作数据集(COLLAB),实验结果如下:

其中,GraphSAGE是采用全局平均池化;DiffPool-DET是一种DiffPool变体,使用确定性图聚类算法生成分配矩阵;DiffPool-NOLP是DiffPool的变体,取消了链接预测目标部分。总的来说,DiffPool方法在GNN的所有池化方法中获得最高的平均性能。
为了更好的证明DiffPool对于图分类十分有效,论文还使用了其他GNN体系结构(Structure2Vec(s2v)),并且构造两个变体,进行对比实验,如下表:
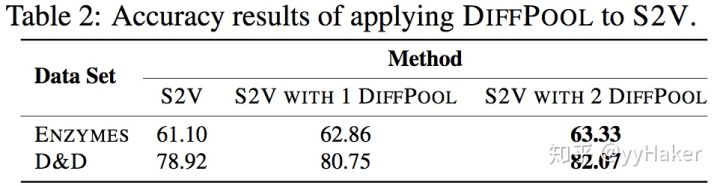
可以看到DiffPool的显著改善了S2V在ENZYMES和D&D数据集上的性能。

而且DiffPool可以自动的学习到恰当的簇的数量。
至此,我们来总结一下DiffPool的优点,
(1)可以学习层次化的pooling策略
(2)可以学习到图的层次化表示
(3)可以以端到端的方式被各种图神经网络整合
然而,注意到,DiffPool也有其局限性,分配矩阵需要很大的空间去存储,空间复杂度为 [公式] , [公式] 为池化层的层数,所以无法处理很大的图。
参考
^Graph Neural Networks: A Review of Methods and Applications. arxiv 2018 https://arxiv.org/pdf/1812.08434.pdf
^A Comprehensive Survey on Graph Neural Networks. arxiv 2019. https://arxiv.org/pdf/1901.00596.pdf
^Deep Learning on Graphs: A Survey. arxiv 2018. https://arxiv.org/pdf/1812.04202.pdf
^GNN papers https://github.com/thunlp/GNNPapers/blob/master/README.md
^Semi-Supervised Classification with Graph Convolutional Networks(ICLR2017) https://arxiv.org/pdf/1609.02907
^如何理解 Graph Convolutional Network(GCN)? https://www.zhihu.com/question/54504471
^GNN 系列:图神经网络的“开山之作”CGN模型 https://mp.weixin.qq.com/s/jBQOgP-I4FQT1EU8y72ICA
^Inductive Representation Learning on Large Graphs(2017NIPS) https://cs.stanford.edu/people/jure/pubs/graphsage-nips17.pdf
^Graph Attention Networks(ICLR2018) https://arxiv.org/pdf/1710.10903
^Variational Graph Auto-Encoders(NIPS2016) https://arxiv.org/pdf/1611.07308
^VGAE(Variational graph auto-encoders)论文详解 https://zhuanlan.zhihu.com/p/78340397
^Hierarchical Graph Representation Learning withDifferentiable Pooling(NIPS2018) https://arxiv.org/pdf/1806.08804
转载于:https://zhuanlan.zhihu.com/p/136521625


