迭代实现二叉树的遍历-算法通关村

迭代实现二叉树的遍历-算法通关村

---

• 理论上，递归能做的迭代一定能做，但可能会比较复杂。有时候面试官要求不使用递归实现三种遍历，递归就是每次执行方法调用都会先把当前的局部变量、参数值和返回地址等压入栈中，后面在递归返回的时候，从栈顶弹出上一层的各项参数继续执行，这就是递归为什么可以自动返回并执行上一层方法的原因。

---

1 迭代法实现前序遍历

• 前序遍历是中左右，如果还有左子树就一直向下找。完了之后再返回从最底层逐步向上向右找。
  不难写出如下代码：（注意代码中，空节点不入栈）

•   public List<Integer> preOrderTraversal(TreeNode root){
            List<Integer> res = new ArrayList<>();//存放遍历的结果
            if(root == null){
                return res;
            }
            Deque<TreeNode> stack = new LinkedList<>();
            TreeNode node = root;
            while(!stack.isEmpty() || node != null){
                while(node != null){//空节点不入栈
                    res.add(node.val);
                    stack.push(node);
                    node = node.left;
                }
                //当当前节点的所有左子节点都已遍历后，
                // 将栈顶元素出栈，并将node更新为该节点的右子节点。
                // 然后继续执行内部循环，遍历右子树。
                node = stack.pop();
                node = node.right;
            }
            return res;
        }
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21

---

2 迭代法实现中序遍历

• 中序遍历是左中右，先访问的是二叉树左子树的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进res列表中）。在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。看代码：

•   public List<Integer> inOrderTraversal(TreeNode root){
            List<Integer> res = new ArrayList<>();
            Deque<TreeNode> stack = new LinkedList<>();
            while(!stack.isEmpty() || root != null){
                while(root != null){
                    //将当前节点入栈，并将root更新为其左子节点。
                    // 这个循环会一直执行，直到当前节点为空，
                    // 即遍历完当前节点的所有左子节点。
                    stack.push(root);
                    root = root.left;
                }
                root = stack.pop();
                res.add(root.val);
                //将root更新为该节点的右子节点，以便后续遍历右子树
                root = root.right;
            }
            return res;
        }
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18

---

3 迭代法实现后序遍历

• 后序遍历的非递归实现有三种基本的思路：反转法、访问标记法、和Morris法，可惜三种理解起来都有些难度，如果头发不够，可以等一等再学习。
  个人感觉访问标记法是最难理解的方法，而Morris法是一个老外发明的巧妙思想：不使用栈，而是用好树中的nul指针，但是实现后序仍然非常麻烦，我们这里不再展开，感兴趣的同学可以查一
  下。

• 这里只介绍一种好理解又好实现的方法：反转法。

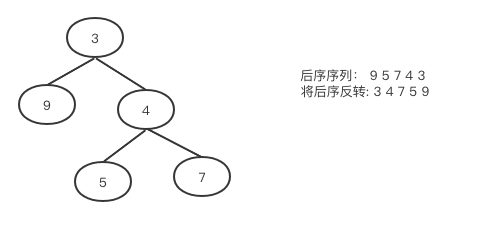
• 如下图，我们先观察后序遍历的结果是 seq = { 9 5 7 4 3 }，如果我们将其整体反转的话就是
  new_seq = {3 4 7 5 9}.

• 

• 有没有发现要得到new_seq的方法和前序遍历思路几乎一致，只不过是左右反了。前序是先中间，再左边然后右边，而这里是先中间，再后边然后左边。那我们完全可以改造一下前序遍历，得到序列new_seq之后再reverse一下就是想要的结果了，代码如下：

•   public List<Integer> postOrderTraversal(TreeNode root){
            List<Integer> res = new ArrayList<>();
            if(root == null){
                return res;
            }
            Deque<TreeNode> stack = new LinkedList<>();
            TreeNode node = root;
            while(!stack.isEmpty() || node != null){
                //将当前节点的值添加到结果列表res中，
                // 然后将当前节点入栈，并将node更新为其右子节点。
                // 这个循环会一直执行，直到当前节点为空
                while(node != null){
                    res.add(node.val);
                    stack.push(node);
                    node = node.right;
                }
                node = stack.pop();
                //将node更新为该节点的左子节点，以便后续遍历左子树。
                node = node.left;
            }
            //列表中的顺序是左子树-右子树-根节点。
            // 但是后序遍历的正确顺序应该是左子树-右子树-根节点，
            // 所以需要将结果列表res反转。
            Collections.reverse(res);
            return res;
        }
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21
  22
  23
  24
  25
  26

  
  
  1
  2