k-means聚类算法详解_kmeans算法_简述k-means聚类分析的基本步骤

聚类算法是先有数据在来分类。

一. 算法步骤

1、首先确定一个k值，即我们希望将数据集经过聚类得到k个集合。

2、从数据集中随机选择k个数据点作为质心。

3、对数据集中每一个点，计算其与每一个质心的距离（如欧式距离），离哪个质心近，就划分到那个质心所属的集合。

4、把所有数据归好集合后，一共有k个集合。然后重新计算每个集合的质心。

5、如果新计算出来的质心和原来的质心之间的距离小于某一个设置的阈值（表示重新计算的质心的位置变化不大，趋于稳定，或者说收敛），我们可以认为聚类已经达到期望的结果，算法终止。

6、如果新质心和原质心距离变化很大，需要迭代3~5步骤。

二. 算法优缺点

优点：

1、原理比较简单，实现也是很容易，收敛速度快。

2、当结果簇是密集的，而簇与簇之间区别明显时, 它的效果较好。

3、主要需要调参的参数仅仅是簇数k。

缺点：

1、K值需要预先给定，很多情况下K值的估计是非常困难的。

2、K-Means算法对初始选取的质心点是敏感的，不同的随机种子点得到的聚类结果完全不同 ，对结果影响很大。

3、采用迭代方法，可能只能得到局部的最优解，而无法得到全局的最优解。

三. 算法实现

算法使用sklearn实现：

step 1 创建数据集合：

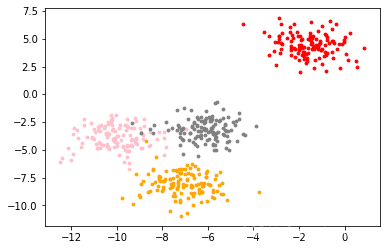
首先我们创建一个由500个样本构成的数据集合，我们首先将自定义划分为四类。

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
#自己创建一个大小为500的数据集，由两维特征构成
X, y = make_blobs(n_samples=500,n_features=2,centers=4,random_state=1)

1
2
3
4
5

具体长这样：

color = ["red","pink","orange","gray"]
fig, ax1 = plt.subplots(1)
for i in range(4):
    ax1.scatter(X[y==i, 0], X[y==i, 1]
                ,marker='o' #点的形状
                ,s=8 #点的大小
                ,c=color[i]
                )
plt.show()

1
2
3
4
5
6
7
8
9
10

setp 2 基于分布进行聚类

首先，我们要猜测一下，这个数据中有几簇？
先猜测为3簇

from sklearn.cluster import KMeans
n_clusters = 3#首先测试的超参数
cluster = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
y_pred = cluster.labels_
centroid = cluster.cluster_centers_

1
2
3
4
5
6

其中n_clusters代表我们聚类的簇数，y_pred代表对应元素聚类的类别，centroid代表每个类别的中心点。
现在我们打印一下聚类结果：

color = ["red","pink","orange","gray"]
fig, ax1 = plt.subplots(1)
for i in range(n_clusters):
    ax1.scatter(X[y_pred==i, 0], X[y_pred==i, 1]
                ,marker='o'
                ,s=8
                ,c=color[i]
                )#循环画小样本预测点的位置
    ax1.scatter(centroid[:,0],centroid[:,1]
                ,marker="x"
                ,s=18
                ,c="white")#循环画质心的位置
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14

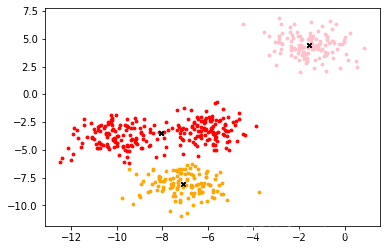
发现效果还不错！
但是我们最开始生成的是四类数据，同样的我们以四类来进行聚类试试？
并且我们顺便打印一下聚类效果

from sklearn.cluster import KMeans
n_clusters = 4#首先测试的超参数
cluster = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
y_pred = cluster.labels_
centroid = cluster.cluster_centers_
color = ["red","pink","orange","gray"]
fig, ax1 = plt.subplots(1)
for i in range(n_clusters):
    ax1.scatter(X[y_pred==i, 0], X[y_pred==i, 1]
                ,marker='o'
                ,s=8
                ,c=color[i]
                )#循环画小样本预测点的位置
    ax1.scatter(centroid[:,0],centroid[:,1]
                ,marker="x"
                ,s=18
                ,c="white")#循环画质心的位置
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

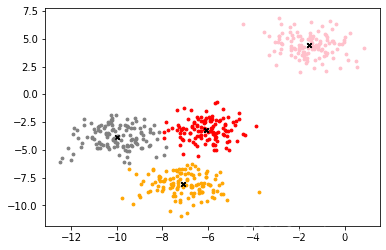
和我们的原始数据比较一下：

效果不错！
但是这样问题就来了
我们如何去衡量一个K值得选取是否合适呢？

四. 聚类效果测评

被分在同一个簇中的数据是有相似性的，而不同簇中的数据是不同的，当聚类完毕之后，我们就要分别去研究每个簇中的样本都有什么样的性质。
根据聚类效果，我们追求“簇内差异小，簇外差异大”。而这个“差异“，由样本点到其所在簇的质心的距离来衡量。
对于一个簇来说，所有样本点到质心的距离之和越小，我们就认为这个簇中的样本越相似，簇内差异就越小。而距离的衡量方法有多种，令

x

x

x表示簇中的一个样本点，

μ

\mu

μ表示该簇中的质心，

n

n

n表示每个样本点中的特征数目，

i

i

i表示组成点

x

x

x的每个特征，则该样本点到质心的距离可以由以下距离来度量:

欧几里得距离

d

(

x

,

μ

)

=

∑

i

=

1

n

(

x

i

−

μ

i

)

2

d(x,\mu)=\sqrt{\sum^{{n}_{i=1}(x_i-\mu_i)}2}

d(x,μ)=∑i=1n​(xi​−μi​)2

​

采用欧几里得距离，则一个簇中所有样本到质心的距离平方和为：

C

S

S

=

∑

j

=

0

m

∑

i

=

0

n

(

x

i

−

μ

i

)

2

CSS = \sum^{{m}_{j=0}\sum}{n}_{i=0}(x_i-\mu_i)^2

CSS=∑j=0m​∑i=0n​(xi​−μi​)2

T

o

t

a

l

C

S

S

=

∑

l

=

1

k

C

S

S

l

Total CSS = \sum^{k}_{l=1}CSS_l

TotalCSS=∑l=1k​CSSl​

其中，

m

m

m为一个簇中样本的个数，

j

j

j是每个样本的编号。这个公式被称为簇内平方和(cluster Sum of Square),又叫做

i

n

e

r

t

i

a

inertia

inertia。而将一个数据集中的所有簇的簇内平方和相加，就得到了整体平方和(Total Cluster Sum of Square)，又叫做

T

o

t

a

l

i

n

e

r

t

i

a

Total inertia

Totalinertia。

T

o

t

a

l

I

n

e

r

t

i

a

Total Inertia

TotalInertia越小，代表着每个簇内样本越相似，聚类的效果就越好。因此K-Means追求的是，求解能够让

I

n

e

r

t

i

a

Inertia

Inertia最小化的质心。实际上，在质心不断变化不断迭代的过程中，总体平方和是越来越小的。我们可以使用数学来证明，当整体平方和最小的时候，质心就不再发生变化了。如此，K-Means的求解过程，就变成了一个最优化问题。

代码实现

inertia = cluster.inertia_

1
2

对，就这么简单
然后我们探究一下刚刚数据中k大小与这个

T

o

t

a

l

自我介绍一下，小编13年上海交大毕业，曾经在小公司待过，也去过华为、OPPO等大厂，18年进入阿里一直到现在。

深知大多数Python工程师，想要提升技能，往往是自己摸索成长或者是报班学习，但对于培训机构动则几千的学费，着实压力不小。自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

因此收集整理了一份《2024年Python开发全套学习资料》，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友，同时减轻大家的负担。

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，基本涵盖了95%以上前端开发知识点，真正体系化！

由于文件比较大，这里只是将部分目录大纲截图出来，每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频，并且后续会持续更新

如果你觉得这些内容对你有帮助，可以扫码获取！！！（备注Python）

深知大多数Python工程师，想要提升技能，往往是自己摸索成长或者是报班学习，但对于培训机构动则几千的学费，着实压力不小。自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

因此收集整理了一份《2024年Python开发全套学习资料》，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友，同时减轻大家的负担。

[外链图片转存中…(img-83rORAcm-1712877047896)]

[外链图片转存中…(img-5Raa739U-1712877047896)]

[外链图片转存中…(img-WIUJR9P6-1712877047897)]

[外链图片转存中…(img-3qr5iK33-1712877047897)]

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，基本涵盖了95%以上前端开发知识点，真正体系化！

由于文件比较大，这里只是将部分目录大纲截图出来，每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频，并且后续会持续更新

如果你觉得这些内容对你有帮助，可以扫码获取！！！（备注Python）