探索 KITTI 数据集：自动驾驶汽车的视觉里程计

什么是 KITTI 数据集？

KITTI 是由卡尔斯鲁厄理工学院和芝加哥丰田技术学院开发的自动驾驶数据集。它是计算机视觉研究中使用的图像和 LIDAR 数据的集合，例如立体视觉、光流、视觉里程计、3D 对象检测和 3D 跟踪。

该数据集可在 http://www.cvlibs.net/datasets/kitti/ 免费下载。

在本文中，我们将探讨 KITTI 里程计数据集的用法。KITTI 数据集是用于评估视觉里程计算法性能的基准数据集。它包含从移动车辆记录的立体图像序列的集合，以及车辆运动的相应地面实况数据。

本文将成为 KITTI 视觉里程计系列的第 1 部分。我们首先回顾执行立体深度估计和视觉里程计任务所需的计算机视觉的一些基础知识，并演示如何在 Python 中使用 OpenCV 实现这些原理。

设置数据集

下载我们打算使用的 velodyne 激光数据(https://www.cvlibs.net/datasets/kitti/user_login.php)和灰度数据(https://www.cvlibs.net/datasets/kitti/user_login.php)，你必须注册并登录才能下载数据集。

下载数据集后，请在包含两个数据集的文件夹的同一路径中创建一个 python 文件。

使用 Python 代码探索数据集

导入所需的依赖项——OpenCV、matplotlib.pyplot、numpy、pandas、os。

现在我们将看一下从数据集中加载轨迹序列之一的地面实况姿势。

poses = pd.read_csv('../dataset/poses/00.txt', delimiter=' ', header=None)
print('Size of pose dataframe:', poses.shape)
poses.head()

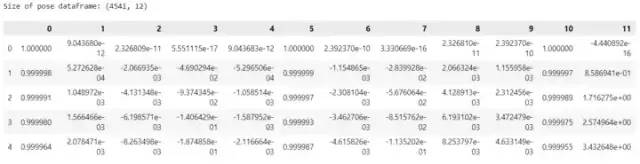
该数据集包含 4541 行和 12 列，其中 4541 是图像帧数，12 是展平 3x4 变换矩阵（外部参数）的结果。该矩阵存储左立体相机相对于全局坐标系的 3x3 旋转矩阵和 3x1 平移向量。

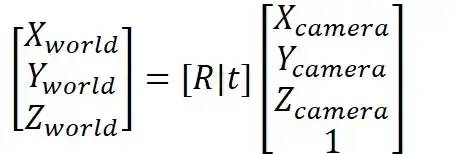
3x4变换矩阵[R|t]存储了相机当前坐标系与相机初始位置坐标系之间的变换。

我们可以通过查看第一个姿势并观察旋转分量是同一的，平移矢量在所有轴上都为零来验证这一点。

first_pose = np.array(poses.iloc[0]).reshape((3,4)).round(2)
second_pose = np.array(poses.iloc[1]).reshape((3,4)).round(2)
print("First pose:\n", first_pose)
print("Second pose:\n",second_pose)

现在我们可以存储所有地面实况姿势，因此我们可以使用它作为姿势序列获得轨迹图，还可以访问这个地面实况数组，其中包含相机相对于全局坐标系的所有位置和方向。

ground_truth = np.zeros((len(poses), 3, 4))
for i in range(len(poses)):
    ground_truth[i] = np.array(poses.iloc[i]).reshape((3, 4))
%matplotlib widget
 
fig = plt.figure(figsize=(7,6))
traj = fig.add_subplot(111, projection='3d')
traj.plot(ground_truth[:,:,3][:,0], ground_truth[:,:,3][:,1], ground_truth[:,:,3][:,2])
traj.set_xlabel('x')
traj.set_ylabel('y')
traj.set_zlabel('z')

从下图中我们可以看到汽车的轨迹具有相同的起点和终点，因为它看起来像一条封闭的路径

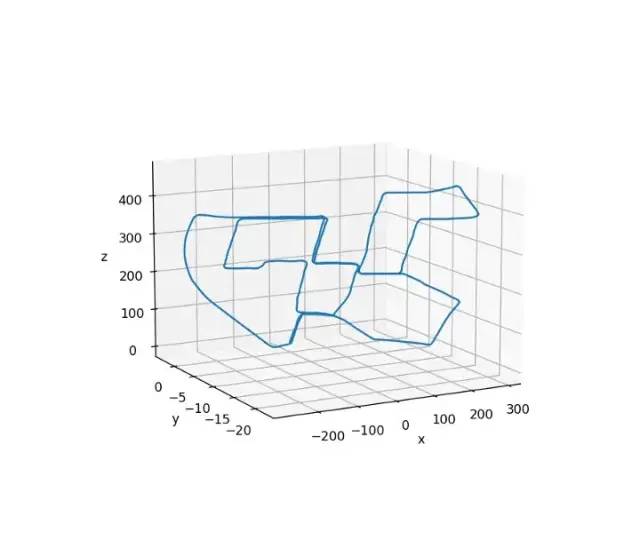
汽车的轨迹

探索立体图像序列数据集

我们现在将加载安装在汽车上的摄像头拍摄的图像。

left_img_files = os.listdir('data_odometry_gray/dataset/sequences/00/image_0') 
 
plt.figure(figsize=(12,6))
plt.imshow(left_img_files[0])
#to check if we have same number of camera poses for each captured image frame
print("left images-",len(left_img_files)) #for sequences/00/image_0= 4541
print("camera poses-",len(poses)) #for dataset/poses/00.txt =4541

每个数据序列的图像帧和姿势的数量是相等的。我们的第一个地面实况姿势是 (0, 0, 0)，因此我们正在跟踪相机相对于第一个相机帧的运动。相机以 10fps 的速率捕获帧，这可以在数据集的每个序列中使用“ times.txt ”文件看到。

times = pd.read_csv('../dataset/sequences/00/times.txt', delimiter=' ', header=None)
times.head() #verify to check frames being captured @10fps

传感器校准

数据集还有传感器校准文件，我们可以加载这些文件来检查它携带的信息。

calibration   = pd.read_csv('data_odometry_gray/dataset/sequences/00/calib.txt', delimiter=' ', header=None, index_col=0)
calibration

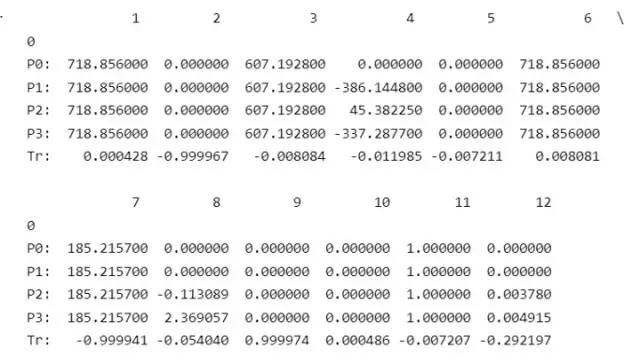
在了解校准文件中的所有这些数字之前，让我们看一下 KITTI 团队提供的传感器配置示意图。

安装有传感器的汽车示意图

上面的示意图显示了四个摄像头，一个是一对灰度立体摄像头，另一对是示意图中标记的 RGB 立体摄像头。左右立体相机之间的距离称为基线，在此配置中为 0.54 m。

回到数据集的校准参数。P0、P1、P2、P3 是相机投影矩阵，其中 P0、P1 用于两个灰度相机，其余两个用于 RGB 相机。Tr 是一个平移向量，它将点从 velodyne 传感器坐标转换到相应的校正相机坐标系。

要深入了解Projection矩阵，在这个数据集中是一个3x4的矩阵，它有相机的内参和外参。

让我们从 calibration.txt 文件数据中打印投影矩阵 P1。

P0 = np.array(calibration.loc['P0:']).reshape((3,4))
P0

投影矩阵

投影矩阵 (P) 是相机的内在矩阵和外在矩阵相结合的结果。

• 内在矩阵包含有关相机焦距和光学中心的信息

• 外在矩阵 (R|t) 使用 3x3 旋转矩阵和 3x1 平移向量表示相机的位姿，该向量将每个相机的坐标系与全局坐标系相关联，这在这种情况下是左灰度相机的坐标系。

通常，相机的投影矩阵用于将全局坐标系中的 3D 点转换为相机图像帧上相应的 2D 像素坐标。然而，该数据集的 calibration.txt 文件中的投影矩阵是经过校正后的，这意味着它将每个相机坐标系的点映射到左侧相机的一个图像平面上。

使用标准相机投影矩阵时，外在矩阵负责将点从全局坐标系转换为相机的坐标系。

从之前显示的示意图中的相机位置来看，如果我们采用全局坐标系的原点（如左侧灰度相机所示）并将其表示为右侧灰度相机的坐标，我们预计 X 坐标为 -0.54，因为左侧相机的原点位于右侧灰度相机原点左侧 0.54 米处。

为了验证这一点，我们可以使用 OpenCV 的函数 cv2.decomposeProjectionMatrix() 将右摄像机的投影矩阵分解为其固有矩阵 (k)、旋转矩阵 (R) 和平移向量 (t)。

分解投影矩阵

P1 = np.array(calibration.loc['P1:']).reshape((3,4))
P1
#decomposing projection matrix
k1,r1,t1,_,_,_,_= cv2.decomposeProjectionMatrix(P1)
 
t1 = t1/t1[3] #for homogeneous coordinates
print("\n",t1)
 
print("intrinsic matrix:\n",k1)
print("rotation matrix: \n",r1)
print("translation vector:\n",t1.round(4))

通过分解投影矩阵，我们能够获得该相机的固有矩阵 (k)、旋转矩阵 (R) 和平移向量 (t)。这些矩阵可用于了解相机如何在全局坐标系中定位和定向，以及它如何捕获 3D 点并将它们投影到其 2D 图像帧中。

内在矩阵

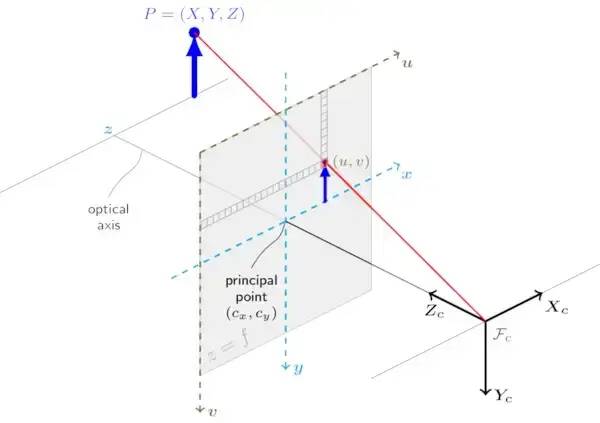
内在矩阵，也称为相机矩阵，是一个描述单个相机内部属性的 3x3 矩阵。它包括有关相机的焦距、主点和倾斜的信息。

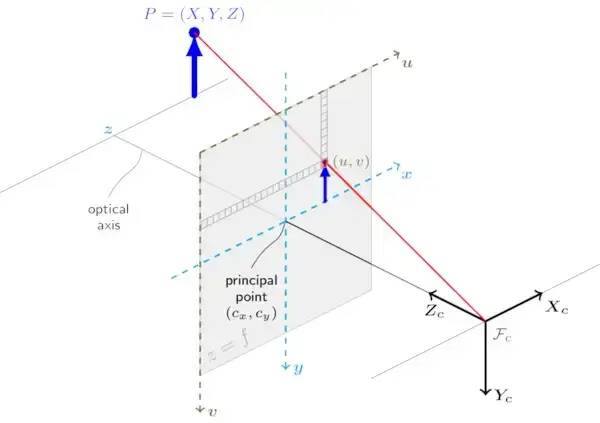
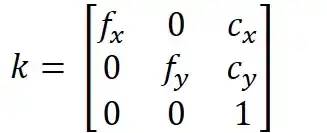
内在矩阵可用于通过透视投影将 3D 世界点映射到 2D 图像点。内在矩阵是相机标定的输出之一，表示为 k。fx，fy 是参数 c_x 和 c_y 的焦距，用于将入射光线映射到相机传感器上的正确像素坐标。这些参数表示图像的光学中心，由于与镜头的轻微错位，它可能不一定位于传感器的中心。此调整可确保相机捕获的图像准确无误。

让我们检查一下与图像比较的光学中心位置

test_img = cv2.imread('data_odometry_gray/dataset/sequences/00/image_0/000000.png')
test_img.shape
cx = k1[0,2]
cy = k1[1,2]
print('Actual center of image (x, y):', (test_img.shape[1]/2, test_img.shape[0]/2))
print('Optical center of image (cx, cy)', (cx, cy))

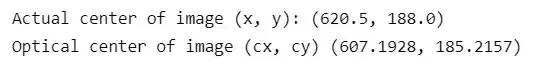
相机校准非常重要，因为它可以解决相机光学中心与图像中心之间的轻微偏差。如果没有这些信息，真实世界中的点在图像上的投影就会不准确。包含 c_x 和 c_y 等参数的内在矩阵用于纠正这种不对齐，并确保投影点正确地映射到相机传感器上适当的像素坐标。

外在矩阵

通过使用从投影矩阵中提取的外在矩阵，我们可以确定全局坐标系原点（如左侧灰度相机所示）在右侧相机坐标系中的位置。示意图表明我们应该期望原点在右侧相机框架的左侧 0.54 米处。

extrinsic_mat = np.hstack([r1, t1[:3]]) #dropping the last row of t1 as it was in homogenous coordinates
extrinsic_mat.round(4)
origin = np.array([0, 0, 0, 1])
T = extrinsic_mat.dot(origin).round(4).reshape(-1,1)
print(T)

投影矩阵的X值为正0.54，说明全局坐标系原点位于相机框右侧0.54米处，说明投影矩阵不是针对右相机，而是针对左相机，右相机的原点被视为全局坐标系。这是因为投影矩阵是立体装置的校正投影矩阵，旨在将多个摄像机坐标系中的点投影到同一图像平面上，而不是将一个摄像机坐标系中的点投影到多个摄像机的图像平面上。

校正后的投影矩阵将传感器坐标系中的 3D 点转换为左侧灰度相机图像平面上的 2D 像素位置。

为了将左侧灰度相机的校正投影矩阵转换为右侧灰度相机的常规投影矩阵，我们分解矩阵，反转外在矩阵并将其与内在矩阵重新组合。

现在让我们尝试找出该点距左侧相机的深度或距离。

pt = np.array([3, 2, 4, 1]).reshape(-1,1)

为了确定一个点距离左摄像头的深度，我们需要将该点转换到左摄像头的坐标系中，然后取 Z 值。

pt_transform = ground_truth[4].dot(pt)
depth_from_left_cam = pt_transform[2]
 
print('point:\n', pt)
print('Transformed point:\n', pt_transform)
print('Depth from left camera:\n', depth_from_left_cam)

我们可以使用这个深度和我们之前获得的内在矩阵 k1 ，来获得我们用来寻找深度的点在图像平面上的投影，这将给我们提供像素坐标。

px_coordinates = k1.dot(pt_transform) / depth_from_left_cam
print('Pixel Coordinates on image plane:', px_coordinates)

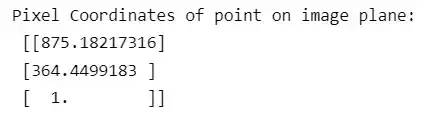
回到原来的 3D 点位置

如果我们知道上面获得的深度，我们还可以通过对上面获得的像素坐标进行归一化，从图像平面上的点的 2D 投影中获得点的 3D 位置。

normalized_pixel_coordinates = np.linalg.inv(k1).dot(px_coordinates)
print('Normalized pixel Coordinates:\n', normalized_pixel_coordinates.T)

从这些归一化坐标中，我们可以恢复原始的3D转换点，因为我们现在知道了深度。这是通过将归一化像素坐标乘以深度来完成的。

为了回到我们选择的原始点来估计原始坐标系中的深度，我们可以采取以下步骤：

1. 在变换矩阵中加入一行 (0, 0, 0, 1) 使其齐次。

2. 反转此齐次变换矩阵。

3. 将倒置矩阵乘以相机帧中恢复的 3D 坐标，最后应将其增加 1 以使其齐次。

pt_3D = normalized_pixel_coordinates.T * depth_from_left_cam
pt_3D.round(4)
print("restored originally transformed 3D point\n",pt_3D.T)
 
transform_homogeneous = np.vstack([ground_truth[4], np.array([0, 0, 0, 1])])
inv_transform_homogeneous = np.linalg.inv(transform_homogeneous)
pt_3D_homogeneous = np.append(pt_3D, 1)
restored_pt = inv_transform_homogeneous.dot(pt_3D_homogeneous)
print("restored original homogeneous point:\n",restored_pt)

为了验证我们是否获得了原始点，你可以检查我们在上一节中估计深度时选择的点，并将它们与恢复的点值进行比较，发现它们与我们之前获得的输出中需要的点值相同，如下所示:

结论

总之，我们探索了数据集，以更好地了解它在视觉里程计领域的用途。它提供了一套全面的立体图像序列以及车辆运动的相应地面实况数据。总的来说，KITTI Odometry 数据集是推进视觉里程计和相关领域最先进技术的重要工具。

参考：

• https://www.cvlibs.net/datasets/kitti/

• https://opencv.org/

☆ END ☆

如果看到这里，说明你喜欢这篇文章，请转发、点赞。微信搜索「uncle_pn」，欢迎添加小编微信「 woshicver」，每日朋友圈更新一篇高质量博文。

↓扫描二维码添加小编↓